新型电力系统混合储能方案优选与优化配置模型研究

田 辉

（陕西昱立电力科技有限公司，陕西 西安 700102）

1 新型电力系统混合储能方案优选

1.1 新型电力系统混合储能方案优选决策指标的构建

为满足新型电力产业的持续化发展需求，构建新型电力系统混合储能方案优选决策指标，为方案优选奠定基础[1]。指标体系结构如图1所示。

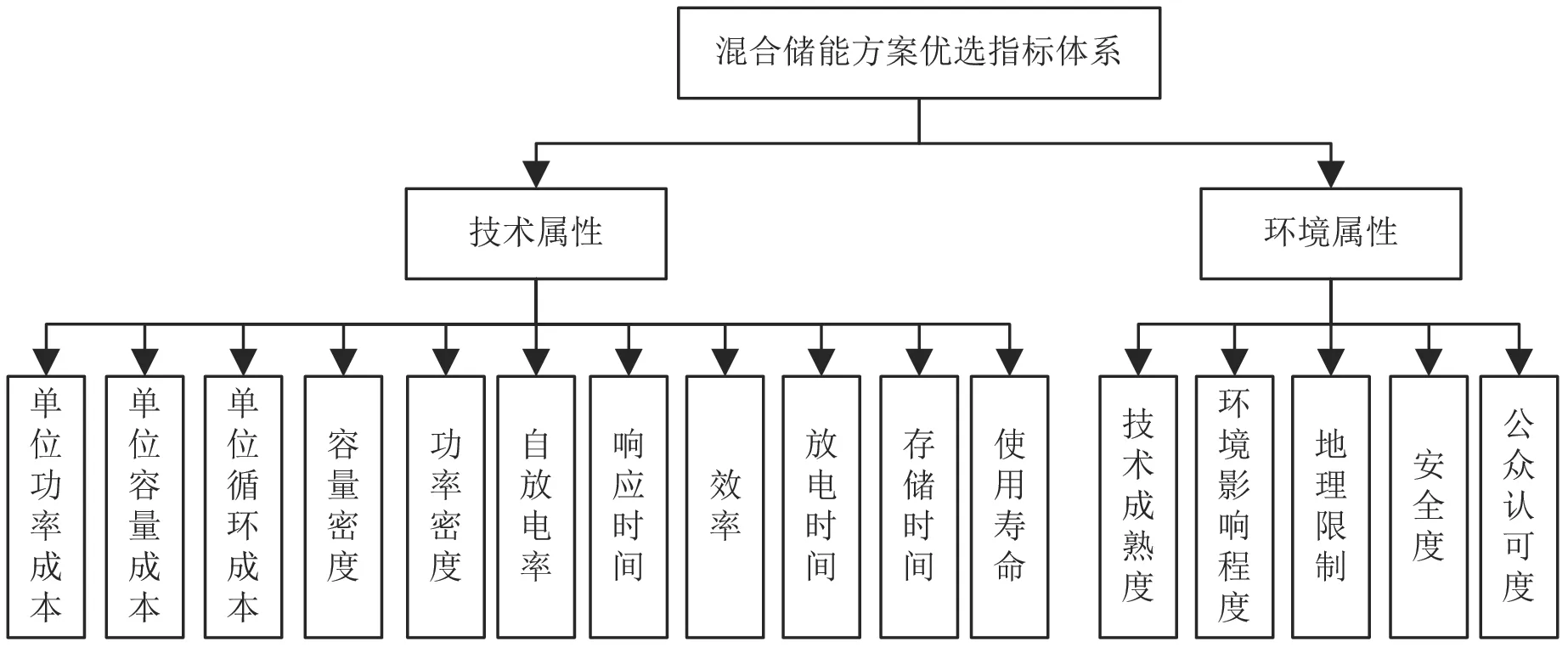
图1 新型电力系统混合储能方案优选决策指标体系

根据相关工作具体要求，将指标按照属性划分为2个主要类别，分别为技术类属性和环境类属性。

构建储能率优化指标体系后，对各种储能率优化的实际情况进行全面剖析，将其作为储能方案优选的前提与基础。在分析单一关键指标发展状况的基础上对储能方案进行关键指标组合分析仅限于对储能技术属性的随机组合，不能全面、稳定地展现出每个关键指标下各储能技术的发展状况。当某种储能技术的关键指标值发生变化时，在随机组合或单一关键指标分析下的储能方案的可行性会出现较大且不规则的整体波动，不利于对储能方案整体发展的分析。因此，按照上述方式，完成指标的初步选择后，有必要结合新型电力系统开发的具体需求，在方案优选过程中进行指标的调整与即时优化。

1.2 基于拉格朗日改进的指标综合赋权

在上述内容的基础上引进拉格朗日改进，对指标进行综合赋权，以掌握在方案优选过程中不同指标的权重与重要性[2]。拉格朗日改进算法是AHP法的分支，也是对复杂问题进行综合量化处理的关键技术手段之一，基于拉格朗日改进的指标综合赋权过程主要由2个步骤构成。步骤一，使用计算机模糊语言，对指标体系中随机2个指标进行矩阵对比，通过此种方式将复杂且定性的指标描述为可用计算机语言表达的IT2TrFNs。步骤二，利用公式（1）进行计算机表达语言IT2TrFNs的处理。

式中：D代表计算机表达语言IT2TrFNs的处理；a代表指标与计算机语言的转化关系；i代表指标与计算机语言的转化次数；U代表模糊数；H代表对比矩阵。

完成上述处理后，进行指标的一致化处理，如公式（2）所示。

式中：CI代表指标的一致化处理；λmax代表对比矩阵的最大特征值；m代表矩阵顺序。

完成处理后，进行指标的校验，校验过程如公式（3）所示。

式中：CR代表指标的校验结果；RI代表指标的一致性指数。

对通过校验的指标进行赋权，如公式（4）所示。

式中：W代表指标综合赋权；j代表第j个指标；e代表指标的信息熵。

按照上述步骤，完成基于拉格朗日改进的指标综合赋权。

1.3 优选决策与储能方案优选效果分析

在上述内容的基础上进行混合储能方案优选场景的构建，将场景构建的过程作为不同储能方案在实际应用中产生数据的非监督学习过程。假设现有若干个可用于新型电力系统的混合储能方案，每个储能方案的作用与集结方式是不同的（集结方式包括容量型、功率型和容量型/功率型等）[3]。参照上述步骤，根据构建的新型电力系统混合储能方案优选决策指标进行方案的优选决策，该过程如图2所示。

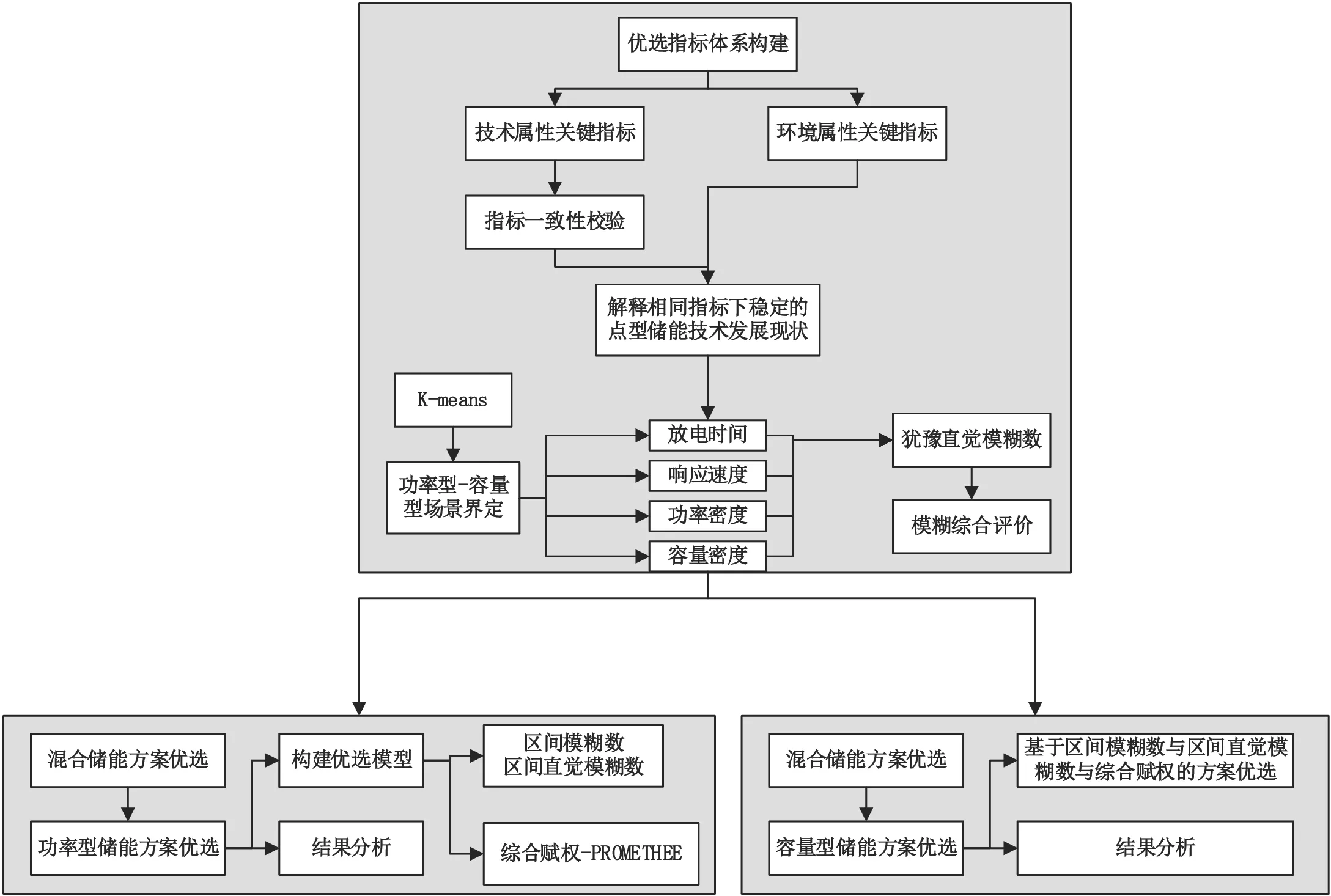
图2 新型电力系统混合储能方案优选决策过程

通过决策掌握不同场景下的新型电力系统混合储能方案优选决策结果。根据结果可知，在容量型场景下，抽水蓄能方案＞压缩空气储能方案＞低温储能方案＞氢燃料电池储能方案（“＞”代表“优于”）。在功率型场景下，电极电容器储能方案＞氢燃料电池储能方案＞飞轮及储能方案。在容量型/功率型场景下，压缩空气储能方案、抽水蓄能类的储能方案更有优势[4]。

为检验所提方案是否能在实际应用中发挥预期作用，本文将某地区大型新能电力发电站作为试点，对储能方案的优选过程进行实践。根据实践可知，所提储能方案优选方法综合应用效果良好，可以在后续的工作中尝试将其投入使用，以此种方式辅助电力工作站等相关负责人的决策。

2 优化配置模型

2.1 波动信号多尺度分解

采用修正的EMD方法，在多时间尺度上对波动性的产、用2条曲线进行分解，以更清晰、直观地展现灵活需求的特征和规律。EMD是一种基于数据本身时间特性的多尺度分解，克服了小波分解设置的基函数无自适应能力的缺点。这种方法不需要对基函数进行设置，可以对任意信号进行科学分解[5]。在电力系统扰动信号的分解过程中，电能的瞬时频率扰动成分通常以低级IMF成分为主，而高级IMF成分通常以低级IMF成分为主。为此，采用EMD分解方法，利用容量性存储技术消除K阶次及以下的输入变量，利用功率性存储技术消除K阶次及以下输入变量的总和，实现系统波动信号的高效分割。在EMD分解前，对信号来说有2个约束条件是必要的。1）约束条件1。在波动信号集合中，极值点数与过零点数应相等，或最多差一个。2）约束条件2。在任一时刻，上包络线、下包络线中的局部最大值的平均值应该是0，在坐标系中，上包络线与下包络线应在时间轴上形成对称。在经过EMD分解后，各IMF应满足公式（5）。

式中：X（t）代表波动信号；rk（t）代表分量信号；res表示留数。

分解完毕后，对分解后的信息进行阈值约束，重新构建各类储能装置所需承担的信号波动调节任务。通常情况下，储能应平抑的功率波动频率不得超过其自身的相应速度，分别如公式（6）、公式（7）所示。

式中：F（ci1）代表i1个IMF信号分量对应中心频带频率；F（ci2）代表i2个IMF信号分量对应中心频带频率；Fb代表功率型储能最高响应频率；Fc代表能量型储能最高响应频率。

基于云模型-OWA算子中的EMD算法并结合群决策思想来提升阈值决策过程的有效性，具体步骤如下。第一步，用EMD模式分解法分解原信号。第二步，对各部分进行量化，利用各部分的平均幅值和频率值的平均比来度量各部分的波动信息，为功率和容量进行分类提供依据。第三步，聚合最大与最小运算符间多属性变量信息，按照从大到小的顺序对原始信息进行重新排列，并对数据的位置进行加权处理，如公式（8）所示。第四步，比较IMF在功率型场景与容量型场景中的结果，通过优势度对比确定信号阈值。

式中：a代表原始参数向量；b代表排序后的结果；ω代表有序数据位置的OWA加权向量。

2.2 构建系统发电侧混合储能优化配置模型

以新一代电网的源端灵活调控需求为切入点，构建多灵活调控源协同互补的混合储能功率与容量优化配置模型。本项目拟进行基于混合储能的新型电网优化配置方法的研究，优化配置建模原理如图3所示。

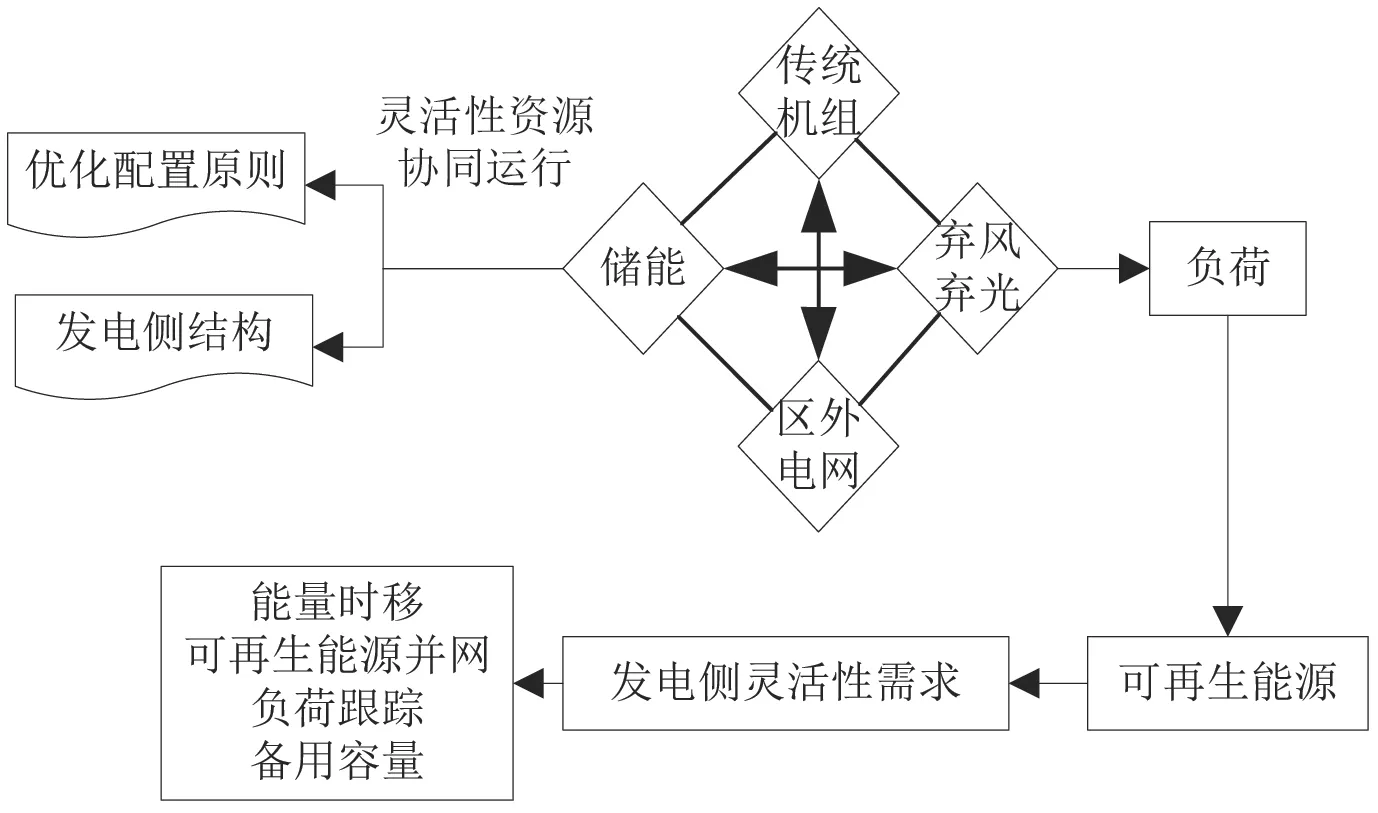
图3 发电侧混合储能优化配置原理图

由于建立的储能系统主要为新型电力系统提供服务，因此其使用寿命不会超过系统本身的使用寿命，残值在上述优化配置模型中可不再考虑，以此确定混合储能的全生命周期投资成本，如公式（9）所示，在此基础上提出一种新的可持续发展能源的管理方法。

式中：Ces，in代表混合储能的全生命周期投资成本；ces，p代表储能单位额定功率建设成本；ces，e代表额定容量建设成本；Pes，rp代表电站额定功率；Ees，re代表电站额定容量；γ代表折现率。

3 结语

混合储能系统是新型电力系统的重要组成部分，具有提高电力系统稳定性、安全性和经济性的优势。为发挥混合储能技术在新型电力系统发电中更高的效能与价值，本文进行了此次研究。通过对模型进行测试得出如下结论。1）混合储能系统在新型电力系统中具有显著优势。与单一的储能技术相比，混合储能方案能更好地满足电力系统的需求，提供短时大功率和高能量密度的能量储存和释放能力。2）本文研究结果进一步揭示了混合储能系统在新型电力系统中的理论和实践意义。它提高了电力系统的运行效率，降低了运行成本，并为实现可再生能源的高效利用提供了新的解决方案。

现阶段的研究已经取得了一些进展，但仍有许多问题需要进一步研究和探索，未来将根据产业发展需求进行进一步的设计，可针对不同类型的混合储能系统进行深入比较，找出各种储能技术的最佳组合方式。此外，混合储能系统的优化策略也需要持续改进，以适应电力系统运行环境的变化和更高层次的需求。