卫星光机载荷热模型参数高效修正方法研究进展

李玉涵，杨宝玉，*，吴亦农，张强，唐晓

1.中国科学院 上海技术物理研究所，上海 200083

2.中国科学院大学，北京 100049

热分析技术是卫星研制过程中的重要技术，在卫星热控制设计、地面试验验证、在轨技术支持中有着重要作用。随着计算机技术的发展，基于有限元的热分析软件建模求解的方法被广泛应用于该问题［1-5］，极大地提高了卫星热分析的效率。但建模过程中不够合理的设置会导致仿真模型不准确，从而使后续仿真计算得到的温度值与卫星热平衡试验温度结果或在轨遥测温度结果存在一定程度的偏差。这种温度结果的偏差一方面会导致高成本的地面试验需要重复进行，另一方面甚至有可能直接影响热控系统在轨运行的有效性。模型的误差主要来自于3 个方面［6］：①模型简化和网格划分过程中引起的模型差异；②数值解不可避免的计算误差；③部分关键热控参数的不确定性［7-12］（如材料导热系数、接触传热系数以及涂层的吸收率/发射率等）。上述3 种引起温度误差的来源中，在模型简化过程所做的假设是合理的条件下，热模型所引入的几何参数是可以确定的。网格划分和计算误差所引起的温度误差通常可以采用分析技术估算出来，其误差也是可控的［13］。因此，当前国内外热控领域研究的重点放在了对所使用的物理参数的不确定性引起的温度误差的讨论上［14-15］。于是，热分析模型的不确定性问题就转化为其中模型参数的不确定性问题，热模型物理参数的有效修正方法也被作为卫星研制的关键技术被广泛研究［15-21］。

卫星光机载荷属于卫星的有效载荷系统，它的热控系统设计的准确性关系到相机的光学效能。因此，通过修正得到合理的热模型，获得正确的热设计对于卫星光机载荷获取高分辨率的地面图像具有重要意义。以极地轨道卫星光机载荷热控模型修正这一具体问题（简称光机载荷热控模型修正）为例，可以参考目前其他部件或其他飞行任务的航天器热模型修正的研究，但是由于控温对象为光学镜头、主结构和焦面组件等［5］，有以下特殊需求：

1）为保证镜头热变形在可接受范围内，对热设计的温度梯度、温度水平和温度稳定性有明确要求。如某型号相机主次镜组件技术指标为（20±1.5）℃，主镜组件周向温度梯度≤1 ℃，TDICCD 器件控温在0～12 ℃内等［5］。

2）由于无法在镜头上布设测点实现温度的直接监测，相机的部分温度指标只能通过热分析进行评估，因此需要精确度更高的仿真预测模型。

3）光机载荷的结构复杂，辐射关系复杂，有限元模型求解时间长；待修正参数多，手动修改参数容易出错且效率低下；由于瞬态计算的需求，对计算机的算力要求较高。因此需要更高效的修正方法。

综上所述，光机载荷热控模型修正任务的特殊性主要体现在瞬态、精确和高效3 个要求上，解决这3 个需求的方法归纳总结后如图1 所示。瞬态问题主要通过得到更适合光机载荷热模型修正问题的参数识别和目标函数解决。模型的精确度与所选择的寻优算法的评价指标有直接的关系，如使用回归算法时通过均方误差（Mean Squared Error，MSE）进行评价，MSE 的值越小，说明预测模型描述试验数据具有更好的精确度。模型修正的效率问题总结了更高效的寻优算法、使用代理模型和开发自动修正工具3 种方法。

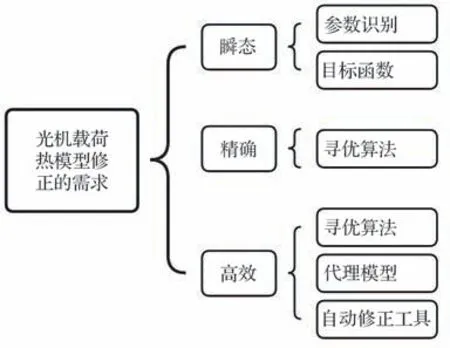
图1 光机载荷热模型修正需求及方法Fig.1 Requirements and methods for thermal model correction of optomechanical loads

本文首先介绍解决航天器热模型修正问题的一般方法，然后鉴于光机载荷热控模型修正任务的特殊需求对每种方法在各节分别进行介绍。需要注意的是，制约瞬态分析和精确度的因素中，除了自身理论方法上的问题外，瞬态分析和更高精确度的需求需要更久的有限元计算和更多的迭代次数，势必会造成更高的时间成本，因此效率问题也一直是一个很重要的因素，且提高效率的方法与提高精确度的方法是有重合的。因此，“高效”是本文的研究重点，将在第2～第4节分别讨论提高效率的3 种方式的新方法，分别为新型寻优算法、构建代理模型和自动修正工具的开发。

1 热模型修正方法

1.1 经典修正方法

对于航天器热模型修正的一般方法，是利用试验测量或在轨遥测的温度数据作为真值，对仿真模型中的待修正参数进行标定［5］，属于一类模型参数的反演问题。一直以来，处理反演问题有2 种方法，即确定性方法和统计方法［22］。确定性方法是将模型参数和实测温度数据都视为确定量，构建热平衡方程，利用解代数方程的方法求解热网络模型参数，所得的解有确定意义。统计方法是将热网络模型参数和求解温度数据都看作随机变量，用统计的方法确定模型温度所服从的概率分布，求得的参数为统计估计值。

针对热模型修正问题，一开始学者们主要采用确定性方法，代表性研究有：Toussaint 等［23］提出用最小化分析-试验能量平衡残差进行模型修正；Ishimoto 等［24］利用线性回归分析的方法近似地得到一个折合辐射传热系数值，通过卡尔曼滤波加入了对于噪声扰动的估计；Shimoji 等［21］提出了用统计回归法进行热网络模型修正，通过对试验数据分析，利用F 检验（方差检验）对重要节点的数据确定置信区间，通过统计学的方法利用最少的试验数据实现了热网络传热系数修正的目的，并成功预测了其他工况的温度，但是该方法极度依赖F 检验，在一定条件下，F 检验会排除部分有效数据，导致得到的结果不全面。

中国在20 世纪70 年代末随着航天工程的发展而开展了航天器热模型修正研究，早期以闵桂荣等［25］为代表，对热分析模型修正的研究开展了理论探索。20 世纪90 年代中期翁建华等［26］提出了综合修正方法，并进行瞬态修正方面的探索研究，总结了国外的残差极小化、卡尔曼滤波法和统计回归等修正方法后，提出了利用稳态数据修正卫星热网络方程及其系数的方法，在理论上取得了较大进展。

随着卫星结构日趋复杂，仿真中的热分析模型结点数目动辄数十万甚至上百万，需修正的参数数量也随之陡增。此时面对修正问题传统的确定性方法已经无法解决，统计学方法应运而生。Harvey 等［27］在设计卫星天线时引入了随机近似方法，分析了天线面对地球和太阳的角度等设计参数以及环境参数的选取及优化。Herrera等［15］首次提出将蒙特卡洛随机近似方法应用于卫星热分析，从此蒙特卡洛法及其改进的方法成为热模型修正方法的主流［28］，时至今日仍有巨大活力，是各种改进方法的基础，因此有必要介绍经典蒙特卡洛法的步骤。

蒙特卡洛法的原理：参数的不确定性主要表现在参数是在一定取值区间内变化的，在实际应用中，理论上每个参数在某一时刻应该只有一个值。因此以待修正参数为自变量，多次抽样后依次代入仿真软件求得温度计算值，通过建立计算值与试验值间的目标函数并求解函数的极值点，得到一组最优的热参数，各监测点的试验温度与仿真温度之间的误差最小时的参数就是理论上的近似解。图2 所示为蒙特卡洛分析的主要步骤［28-29］，主要包括参数识别并确定参数分布区间、参数抽样、确定目标函数、参数寻优等过程。

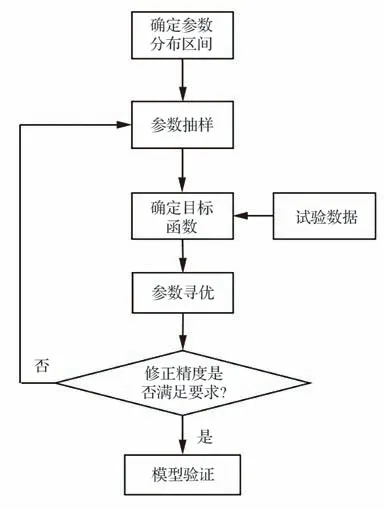
图2 蒙特卡洛分析步骤Fig.2 Analysis steps of Monte Carlo

1.2 热模型修正技术研究进展

近几年关于热模型的修正问题出现了一些新方法。KIM 等［6］采用具有替换矩阵操作的静态压缩算法来处理庞大的矩阵，以卫星面板的热模型为例说明了所开发的归约方法，并对其结果进行了讨论，综述了生成的网格对简化热模型的影响；Anglada 等［30］讨论了遗传算法和基于梯度的方法在热数学模型（Thermal Mathematical Models，TMM）修正中的性能，以国际空间站上的一个真实卫星为例比较了它们的优缺点；Torralbo 等［16］提出了一种使用雅可比矩阵公式和Moore-Penrose 伪逆解决模型与试验TMM 一致性问题的方法，并将其应用于多个工况；Gómez等［31］开发了一种基于统计误差分析和蒙特卡洛法的新方法，以温度不确定度作为概率密度函数，包括了由于每个参数的独立变化而导致的非线性效应，计算结果表明，该方法在计算时间方面与统计误差分析相当，在精度方面与蒙特卡洛法相当；Garmendia 等［32］通过在关键节点建立一个超定方程组，基于梯度的优化算法开发了计算所需最小荷载工况数的表达式。该团队还在另一篇论文［33］中基于控制卫星传热的瞬态方程的误差最小化，提出了一种新的参数识别技术，结果表明，对于中小型瞬态热数学模型，即使在热测试中没有测量一些节点的温度，也可以实现热参数修正分析。

对于国内的相关研究，程梅苏［13］对瞬态热分析模型的修正方法进行了详细研究，研究了修正流程中的响应面优化方法及目标函数对修正结果的影响；钟奇等［34］将遗传算法和Broyden 类的准牛顿法2 种卫星热模型修正新技术引入国内，并初步展望了利用人工神经网络深度学习进行卫星热模型修正的可能性。

由上述研究可知，基于概率统计的改进方法是目前的研究重点，而上述热模型修正大部分针对一般卫星或载荷，对于光机载荷的热模型修正还需要考虑该系统的特定需求，因此将在下文介绍在蒙特卡洛法步骤中光机载荷修正的特殊性。

1.3 光机载荷热模型修正需求

针对光机载荷热控模型修正问题对于瞬态温度计算、高精确度、高效的特殊需求，樊越［35］探讨了最小二乘法、蒙特卡洛法和遗传算法在航空相机热网络模型参数修正中的应用，肯定了遗传算法的优势；李强［36］利用蒙特卡洛法与单纯形法结合的混合法修正了CO2探测仪热分析模型；吴愉华［37］提出了拉丁超立方抽样与Powell 法结合的模型分层修正的方法，对探测器组件进行了热模型修正；林雨霆［38］借助高空气球平台地-月成像光谱仪载荷系统项目，利用Morris 筛选法基于误差反向传播网络（Back Propagation，BP）神经网络代理模型的参数Sobol'敏感性分析方法、BP-Garson 敏感性计算方法进行了全局敏感性分析；李世俊［39］根据整机热平衡试验的结果，提出了一种基于拉丁超立方抽样和坐标轮换法相结合的热分析模型修正方法，并应用于太阳XEUV 成像仪。

总体而言，在传统的蒙特卡洛方法上，演变出了改进的蒙特卡洛法，更适用于解决卫星热模型的修正问题，但专门针对卫星光机载荷的还很少。为满足卫星光机载荷热模型修正的瞬态计算要求，需要在参数识别和目标函数2 点上与一般的航天器热模型修正加以区分。

1.3.1 参数识别

确定待修正参数的类型。通常，卫星热分析普遍采用节点网络法，当热平衡时，节点i有式（1）所示的热平衡关系：

式中：j为与节点i相邻的节点；Dji为结点间传导网络系数；Rji为节点间辐射网络系数；Qi为节点总热源。

而Dji和Rji很难直接检测，但其包含的太阳吸收率αS、半球发射率εH、接触热阻R、材料导热系数λ和材料热容C等则是可检测的，因此修正后者更可信［5］。当针对卫星不同部件的热分析任务时，需要对不同侧重点具体分析决定该部件温度的决定性参数。极地卫星光机载荷热控系统的外热流主要取决于太阳辐射、地球反照和地球热辐射。因此其关键部件温度水平主要取决于卫星的材料性质、表面状态和部件之间的耦合状态。因此修正参数主要包括：材料导热系数λ、材料热容C、涂层吸收率αS、涂层发射率εH和材料间的接触热阻R（包括多层等效热阻R1）。尤其是材料热容C，是区别于一般航天器热模型修正必须要考虑的瞬态计算关键参数。

确定待修正参数的类型之后，按照蒙特卡洛法的步骤，下面需要确定参数的取值区间以进行抽样。蒙特卡洛修正方法一般要求以概率密度函数来描述待修正参数的参数空间，但对于光机载荷热控模型修正问题而言，只能确定热网络模型参数在理论计算值和经验值附近的某一范围内变化，因此以区间来表示。为了对热网络模型的参数空间加以规范，需采用近似概率法对各参数的变化范围加以转化。目前工程中较常规的概率转化形式为均匀分布和正态分布。根据对实际情况的分析，仪器功率等可按电子设备可靠性中对功率不确定性规定直接定义为正态分布；而对于导热系数、表面辐射系数等物性参数取值区间的不确定性较大。杨沪宁等［40］也认为待修正参数的理论值只是一种计算经验值，于是对比了均匀分布和正态分布2 种分布方式，发现较符合光机载荷热控模型参数的概率分布形式为均匀分布。

合理的参数取值区间可以帮助判断参数解的结果是否在合理的物理意义范围内，从而使得修正的结果更有普适性，得到更加有现实意义的结果。但总体而言，目前该部分内容的研究还十分匮乏，主要原因是在待修正参数取值范围确定过程中，实际工程应用中存在诸多不易量化的问题，根据待修正参数类型的不同还有几个难点，如表1 所示。

表1 待修正参数取值难点Table 1 Difficulties in parameter values to be corrected

1.3.2 目标函数

一般热模型的修正可以视为单目标无约束的优化问题［5］。这种目标函数一般是min（OBJECT），OBJECT 是指试验温度数据Ei与计算温度数据Ci相对偏差的某个函数：

式中：在光机载荷热控模型参数修正问题中，节点i需要重点包含光学链路上的所有温度测点。此外，由于对瞬态数据有要求，还需要考虑时间域的问题，目前的方法主要是对OBJECT 在不同时间或多个工况进行累加（再次求和）［13，41］。计算时先对每个部件进行误差计算，然后将所有部件的误差累加后求均方根，最后得到适用于瞬态热分析模型修正的目标函数：

式中：N为每个部件离散点数目；M为工作部件数目；Cji为第j个部件第i个离散点的计算温度，℃；Eji为第j个部件第i个离散点的试验温度，℃。

进一步地，由于每个部件的温度在修正过程中的权重是不同的，将它们各自的误差相加会使得每个部件修正结果差异显著，因此程梅苏［13］将目标函数进行调整，定义为带权重系数的目标函数：

式中：a、b、c分别为部件A、B、C的权重系数；NP=N1+N2+N3+…。

这种目标函数的确定方法更加适合光机载荷热模型修正对于瞬态温度求解的需求。

本节首先介绍了针对一般的航天器热模型修正问题处理方法的演变过程，经过50 年的发展，热模型修正问题主要面临其中参数的修正问题，基于确定性分析的数学方法逐渐不符合日益增大的计算量的需求，以蒙特卡洛法为代表的随机近似方法是目前经典和主流的方法。于是简要介绍了以蒙特卡洛法为基础的改进方法的研究进展。

然后分析了光机载荷热模型修正的特殊需求，对瞬态、精确、高效中的瞬态这一问题从参数识别和目标函数2 个方面介绍了方法上的区别，总结了更适用于光机载荷热模型修正的待修正参数和目标函数公式。

除瞬态的需求外，光机载荷热模型修正还需要解决精确和高效2 个问题，两者所用的方法有所重合，而高效一定程度上是精确的前提，因此后文介绍了3 种提高热模型修正效率的方法。首先分析制约传统穷举法的蒙特卡洛分析效率的原因，主要体现在3 个方面：①穷举法没有方向性，需要大量的样本；②需要重复多次有限元求解，耗时长；③需要较多的人为操作，流程复杂、繁琐且易出错。针对这3 个缺陷，总结有以下3 种解决方法：①通过合适的寻优算法优化参数寻优的方向；②使用神经网络训练代理模型代替有限元计算；③开发自动化修正流程，减少人为操作，合理利用计算机算力以达到最优修正效率。其中第①种方法是当前的研究热点，在热控领域外也有相当多的研究。第②③种方法在热模型修正领域目前的研究者较少，本文总结后提出了一些思考。下文将顺序介绍3 种提高热模型修正效率的方法。

2 寻优算法

2.1 热模型修正寻优算法

热模型修正的目标是寻找那些使仿真计算和试验测量的温度差异尽可能小的不确定参数，这是一个对参数搜索优化的问题。针对热模型修正参数寻优算法这一类问题，已经有诸多学者做过类似的研究。Kim 等［42］提出采用包含局部优化算法的混合遗传算法，通过最小化目标函数来估计壁面发射率；Beck 等［18］引入自适应粒子群优化算法（Adaptive Particle Swarm Optimization，APSO）调整模型参数，以使模型和测试结果一致，调整的参数主要是热导率；Klement［43］使用改良后的Broyden 方法测试算法所需的迭代次数，发现该方法比遗传或自适应粒子群算法所报告的迭代次数小20～1 000 倍；Anglada 等［44］利用遗传算法（Genetic Algorithm，GA）优化了某热设计案例的模型与试验一致性结果，并讨论了遗传算法和基于梯度的方法在热数学模型（Thermal Mathematical Model，TMM）一致性中的性能差异［30］，结论是GA 收敛速度更快。除此之外，还有多岛群遗传算法（Multi-Island Genetic Algorithm，MIGA）［45-46］和模拟退火算法（Simulated Annealing，SA）［47］等。

国内相关研究相对较少，比较有代表性的有：李楠［48］采用遗传算法研究了热传导反问题；程梅苏［13］利用局部优化梯度算法（Broyden，Fletcher，Goldfarb 和Shanno 的姓氏首字母命名，简称BFGS）与GA 对卫星进行了瞬态模型的修正，经BFGS 优化算法修正后的热分析模型所得计算温度与试验温度吻合较好，但是只有敏感度大的传热参数修正结果误差较小，且BFGS 算法是一种局部优化算法，其结果依赖于初始值，而遗传算法虽然不必依赖初始值，经遗传算法修正后热分析模型计算温度误差却较大；钟奇等［34］介绍了遗传算法和Broyden 类的准牛顿法，并就工程实践进行了计算，单从温度修正结果来衡量，这2 种方法均能取得较好效果，但这2 种方法均无法保证不确定参数的精度，甚至只能获得丧失了物理真实性的参数解。

基于上述调研，总结目前的寻优算法，根据计算原理主要分为3 类：基于梯度的算法、进化类算法和基于概率的算法。其中，基于梯度的算法又可以分为梯度下降法、牛顿法、BFGS 法和Broyden 类的准牛顿法几种典型的算法，都属于局部寻优算法，受初始值的选择影响较大，表2［49-54］介绍了不同梯度算法的优劣。而进化类算法和基于概率的算法属于全局寻优算法，受初始值的选择影响较小。后者可以与具有实际物理过程的现象相类比，如表3 所示。

表2 梯度算法对比Table 2 Comparison of gradient algorithms

表3 3 种算法类比Table 3 Analogy of three algorithms

基于梯度的寻优算法中，每一轮搜索方向结束后找到的新的近似值矩阵就是热模型修正领域中的一组参数矩阵。而在进化算法和概率算法中的类比则需参考表3。

通过上述分析可知，为解决高维、非线性、物理意义明确、有高效、精确和瞬态计算需求的光机载荷热控模型修正问题，目前没有哪个单一的寻优算法能够完全符合这一需求。解决这一困难的思路有2 个：①结合使用2 个或若干个寻优算法，通过合理的搭配扬长避短，最终实现光机载荷热控模型修正这一目标；②寻找其他领域如结构修正等领域的新型优化算法，将其他领域中的参数修正方法引入到热模型修正方法中来解决热学问题。

2.2 其他领域寻优算法

模型修正是很多领域共同面临的问题，如热设计、结构力学设计、结构力学修正等领域。这类问题跟热模型修正问题有很多共性，都是通过蒙特卡洛法思想随机近似。具体而言，以1 个CCD 镜头热模型修正［35］和悬臂梁的力学模型修正［55］为例，分析处理光机载荷热控模型修正领域和结构模型修正领域的方法，如表4 所示。

表4 参数修正问题类比Table 4 Analogy of parameter correction question

修正问题与设计优化问题实际上是一对反问题，区别一方面体现在目标函数上，修正问题是使修正的模型预测值接近试验值，而设计优化问题的目的是使设计模型的预测值接近设计要求值，如需将设计优化问题的方法应用于修正问题，可将修正问题（表4）中的TM和SM这2 个试验测得的值更改为TD和SD这2 个设计值。区别的另一方面体现在模型的验证和确认上，修正问题是以最终模型的预测精度判断修正效果的优劣，而设计问题则考察设计的可靠性和鲁棒性以判断设计的优劣。除上述区别外，修正与设计问题不论是结构模型还是热模型，都是在一定程度上将有限元模型视作一个“黑盒”，通过参数的寻优得到最优模型，这一解决问题的思路是相通的。

基于上述分析，热设计、结构设计和结构参数修正这3 种问题与热模型修正问题所使用的方法是可以互相借鉴的，因此可以简要介绍这些其他领域中所使用的寻优算法，为热模型修正提供思路。例如，李守巨［52］估计岩土力学模型参数是通过比较现场观测到的信息数据与理论模型得到的模型数据的差异，建立了模拟退火-蚁群联合算法；王晓军等［56］提出了一种新的基于超体积迭代策略（Hypervolume Iteration，HVI）的全局寻优算法，可以实现快速、稳定的全局寻优，并将HVI 算法与遗传算法和模拟退火法等经典算法从计算效率上进行了比较，验证了该算法的上述特点；Ghosh 等［57］采用高斯过程代理建模和约束贝叶斯优化的高效计算方法优化了针翅片阵列形状设计流程；熊琰等［58］将贝叶斯推理框架与神经网络代理卫星热物理模型相结合，提供了一种卫星热设计智能优化策略；Rezk 等［59］引入了一种基于随机分形搜索（Stochastic Fractal Search，SFS）的优化算法，用于估计准确可靠的太阳能光伏参数值，以便对其进行精确建模；Yang 等［60］使用双层策略构建了具有涂层和配置的最佳设计变量的卫星天线；Otaki 等［61］利用贝叶斯优化与集总热容网络模型相结合的方法，有效地加快瞬态加热芯片电子电路板布局的热设计优化。

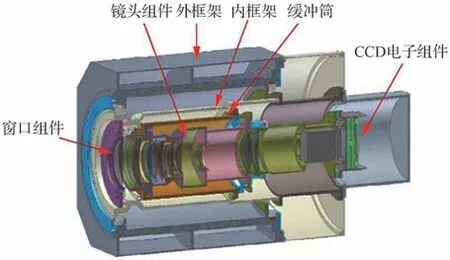
图3 CCD 相机物理模型［35］Fig.3 Physical model of CCD camera［35］

图4 悬臂梁物理模型Fig.4 Physical model of cantilever beam

在遗传算法的基础上进行的各种改进也有着巨大活力，Chang 等［62］通过多岛遗传算法优化了插齿刀几何参数设计流程；Babalik 等［63］受到果蝇嗅觉和视觉行为的启发，开发了果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）来解决持续优化问题；Rao 等［64］采用蜘蛛猴（Spider Monkey Optimization，SMO）算法对宽带EBG架构进行优化设计，以提高微带天线的性能。

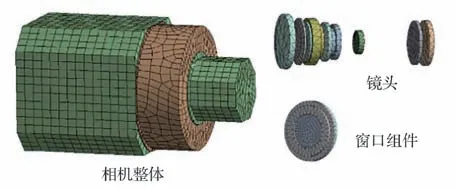
图5 CCD 相机有限元模型［35］Fig.5 FEM of CCD camera［35］

图6 悬臂梁有限元模型［55］Fig.6 FEM of cantilever beam［55］

类似的针对热学、力学结构的设计优化和修正算法还有若干，基于近年开发的新算法在解决设计优化问题和结构力学参数修正问题上的相似性，在光机载荷模型修正问题上这些算法也值得参考。

本节中针对传统穷举蒙特卡洛法的问题提出了第1 个提高修正效率的思路——寻优算法。按照热模型修正领域已有的寻优算法和其他领域中新兴的寻优算法分别总结了寻优算法的研究进展。其中，在热模型修正领域中，对比分析了各种基于梯度的优化算法的优劣，以及基于进化和概率算法的类比和优劣。在其他领域中，首先分析了热学、力学结构设计优化和修正与热模型修正问题的相似性，然后介绍了这些领域中新兴的算法。

在使用寻优算法进行参数寻优的过程中，根据流程图7，发现每次运算结束后需要以合适的方向寻找下一个参数组合矩阵，代入有限元模型中进行计算，这个过程是一个需要反复迭代有限元计算的过程。思考如下：这种有限元计算后建立的输入参数与输出温度之间的关系是通过有限元分析辐射视角系数和各种热耦合而来，但这种关系其实无法以一个显式的数学函数直接由输入求解输出。如果将输入和输出的关系以一个“黑盒”表示，放弃其中无法显化的函数关系，将有限元计算中输入参数包含的物理意义体现在这个“黑盒”的输入参数的取值区间上，理论上可以替代有限元计算进行参数寻优。当然，这个“黑盒”需要在一定置信区间内准确预示有限元运算结果。这种“黑盒”就是代理模型。

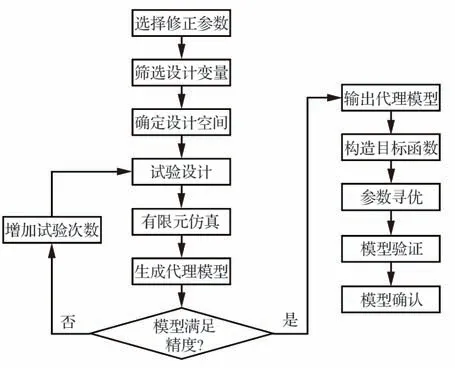
图7 参数修正流程图Fig.7 Flowchart of parameter correction

3 代理模型

代理模型也被称为近似模型、元模型或模拟器，通过插值或拟合的方法构建一个简单的数学模型，再基于代理模型完成对待测点响应值的预测，替代计算耗时的有限元仿真模型的一种方法，从而解决直接使用热分析仿真模型计算带来的计算量庞大的问题，提高模型修正的效率。代理模型在卫星光机载荷热模型修正领域中目前主要是在敏感性分析步骤中运用，该步骤主要用于筛选对温度结果影响较大的敏感参数，从而减少待修正参数的个数，降低问题的维度。但目前这种代理模型代替有限元计算的方法在热模型参数寻优中鲜见研究。首先介绍目前在敏感性分析中应用的代理模型，然后分析代理模型在参数寻优步骤中实现的可行性。

3.1 热仿真修正代理模型

敏感性分析是参数寻优的前序工作，基于代理模型的热模型敏感性分析方法近年逐步被应用于热模型修正领域，如Shahsavani 等［65］提出使用代理模型对模型输出进行基于方差的敏感性分析，验证了代理模型可以大幅降低复杂确定性模型敏感性分析的计算成本；杨雨霆［38］采用了基于BP 神经网络代理模型的参数Sobol'敏感性分析方法，得到了参数的第一阶与总阶敏感性指数值，模型预测效果绝对误差不超过2.5 K，相对误差不超过1%，两者变化趋势也比较吻合，如图8所示。

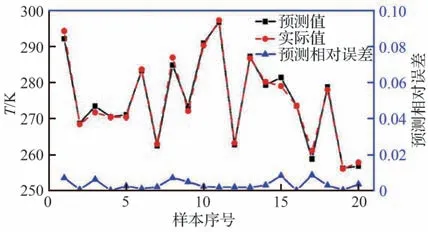
图8 BP 神经网络预测结果与仿真实际结果对比［38］Fig.8 Comparison between BP neural network prediction results and simulation actual results［38］

Yang 等［66］提出了一种基于BP 神经网络代理模型的热设计参数全局敏感性分析方法，通过代理模型提高抽样与热分析模型的效率；员婉莹［67］利用贝叶斯理论、Metropolis-Hastings准则和Edgeworth 级数建立基于重要抽样的参数可靠性全局敏感性分析的单层分析公式，利用Kriging 代理模型自适应构造近似最优重要抽样概率密度函数，统一可靠性与参数可靠性全局敏感性分析，将参数可靠性全局敏感性分析的关键问题转化为无条件重要抽样样本安全或失效状态的识别问题，实现重复利用一组无条件重要抽样样本计算得到所有不确定性分布参数对可靠性的影响；熊琰［68］针对空间相机的热设计问题通过热分析代理模型各个输入参数对应输出分布的累计函数来表征其基于密度的敏感性指数，这是目前首次将基于迁移学习（Transfer Learning，TL）和可适应多种工况的代理模型应用于空间望远镜热分析代理建模，值得借鉴。

如前所述，尽管使用代理模型法能够提高修正效率，但目前代理模型在热模型修正领域还是主要应用于敏感性分析。从原理上讲，代理模型都是依据若干计算或试验的输入输出数据而训练得到的“黑盒”，无论是应用于敏感性分析还是其他领域，方法应该是通用的，代理模型也值得在光机载荷热模型参数寻优步骤中加以引用。但是，由于卫星光机载荷热模型修正问题具有物理意义明确、非线性强、空间高维的特点，还是有必要对其他领域中的代理模型法进行适应性解释和引进。

3.2 其他领域代理模型

根据构建方法不同，其他领域中常用的代理模型可分为插值型代理模型与拟合型代理模型［69］。插值型代理模型主要有径向基函数模型［70-71］（Radial Basis Function，RBF）与Kriging代理模型［72-74］，拟合型代理模型主要有多项式回归模型（Polynomial Regression，PR）、人工神经网络模型［75］（Artificial Neural Network，ANN）、支持向量回归模型［76-77］（Support Vector Regression，SVR）以及多元适应性回归样条模型［9］（Multiple Adaptive Regression Spline，MARS）。

近年其他领域基于代理模型的分析仍在继续。Zhao 等［78］基于动态Kriging 代理模型，联合遗传算法与广义模式下的搜索算法选择最优基函数和相关参数，从而提高了代理模型构建的准确度；Zheng 等［79］联合RBF 模型与Kriging 代理模型，提出一种混合可变保真度（Hybrid Variable-Fidelity）的近似模型，提高了代理模型构建的准确度；Tao 等［80］提出了一种基于多保真替代模型的优化框架，其中将深度置信网络（Deep Belief Networks，DBN）作为低保真模型，然后将多保真代理模型嵌入到机器学习中经典的粒子群算法框架中对马赫数不确定下的翼型进行鲁棒性优化，优化效率明显优于传统的高保真模型；Bartz 等［81］提出了一种基于代理模型的超参数优化方法，可以通过深度学习（Deep Learning，DL）对复杂物理模型进行高精度拟合，同时实现对多个超参数的自适应优化，等等。

如何以合适的方法选择其他领域中的代理模型法以合理应用于热模型修正领域，是引入代理模型法的关键。由于光机载荷热控模型修正问题具有物理意义明确、非线性强、空间高维的特点，需要选择能够表述物理意义、能够解决非线性和高维问题的代理模型。Jin 等［82］系统地比较了4 种流行的元建模技术——PR、MARS、RBF 和Kriging，发现对于高阶非线性和大规模问题，RBF 在平均精度和鲁棒性方面表现最好，但当样本量变少时，RBF 的性能会显著下降；对于低阶非线性和大规模问题，Kriging 在平均精度和鲁棒性方面表现最好，Kriging 的平均精度略高于RBF 和MARS。总结目前相关代理模型的优缺点见表5［83-86］。

表5 其他领域不同代理模型优劣Table 5 Advantages and disadvantages of different surrogate models in other fields

基于上述分析，在热模型修正领域中，为提高修正效率，并满足解决这一特定问题的需求，更建议Kriging 代理模型，当数据量足够大时，也可以考虑RBF 代理模型，或者混合使用代理模型合理避开单一模型的短板。

在本节中，介绍了提高热模型修正效率的另一种方法——利用代理模型代替有限元计算。然后从目前热模型修正领域已有的代理模型法和其他领域中值得借鉴的代理模型法2 方面简要介绍了其原理，并分析了几种代理模型的优劣，给出了相关建议。

值得注意的是，这种用代理模型代替有限元计算的方法使用前需要先明确代理模型预测有限元计算结果的精确度，这一步会额外带来一部分误差，但其误差是可控的，且能够较大地提高计算效率，因此不失为是一种比较有前景的方法。

基于上述分析，现在的蒙特卡洛法已经在很大程度上得到了丰富。随着修正步骤越来越复杂，人为操作可能会有不必要的失误，且制约了效率的进一步提升，于是自动修正工具应运而生。

4 自动修正工具

4.1 修正工具开发现状

为提高修正效率，目前有少量的针对热模型实现修正过程自动化的工具开发研究，可以大幅简化热分析模型修正工作，同时提升预测模型的精确度。目前最接近实现这一功能的是Frey 等［87-88］基于MATLAB 开发的一种新工具TAUMEL（Tool for AUtomated Model Correlation using Equation Linearization）。它的构建模块如图9 所示。它可以自动修正热模型，该工具可以自动导入热试验数据，在MATLAB 中实现寻优，已在小型和大型设备上成功测试，但是依然需要反复将参数取值代入到热仿真软件中迭代计算，制约了运算效率的提高。随着代理模型的发展，从TAUMEL 工具出发，若以该工具的架构为基础，再结合代理模型的应用，可形成一个更加完善可行的方案。

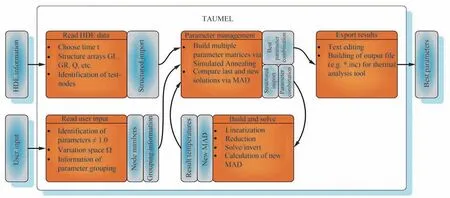
图9 TAUMEL 和执行逻辑的程序构建模块［87-88］Fig.9 Program building module for TAUMEL and execution logic［87-88］

能够实现类似功能的研究还有：陈文［55］以风机叶片为研究对象，基于Msc.Patran/Nastran 软件的二次开发平台，利用其提供的PCL二次开发语言，开发了基于敏感性和模拟退火方法的2 个模型修正模块，在Patran 中增加了模块操作的人机交流界面，使用MSC 商用软件的有限元建模与分析功能，所开发的模块能够完成复杂工程结构领域的有限元模型修正任务；李欢欢等［89-90］选择I-DEAS 为温度场分析模块的支撑软件进行温度场分析，研究了基于内嵌机制和外部开发机制的I-DEAS 软件的二次开发技术，实现了星载抛物面天线热分析求解的自动化执行。这类工具在实现流程上与热模型修正流程自动化有相似性，都需要使用优化平台和仿真软件进行联合，形成完善的工作流自动化进行修正。在此基础上，我们认为光机载荷热模型修正流程自动化应该是可行的，因此做出了如下思考。

4.2 修正工具思考

首先分析各国学者提出的修正流程自动化工具依然未能广泛实现工程化应用的问题来源，主要在于：①修正结构不完善，未能将最新的方法纳入工具中使用；②工具结构较为松散，不同模块之间的连接不够明显，与仿真软件的接口不够强大，需要使用的热工程师具有一定的二次开发编程能力。因此，如果有一个合适的平台能够将参数识别、有限元计算、代理模型、寻优算法这一系列完整的步骤集成在一个工作流中，让热设计工程师在一个界面中实现全部操作，并使每一步操作显化，有助于解决当前优化工具的工程化应用问题。为给予后续优化工具或集成优化平台的研究更多参考，结合李欢欢［89］的分析，本文总结了目前常用的航天领域热仿真软件及各自的适用情况和局限性，见表6。为使仿真计算与参数寻优过程集成，在流程上更为规范和高效，使用多学科优化平台是一种很好的思路。这种优化平台通过搭建工作流的方式可以将参数抽样、仿真计算、结果导出与寻优计算进行集成。如2016 年，施道云等［91］提出了一种基于Isight/Fluent 协同仿真的热模型修正方法，提高了热模型修正精度，但是分析的模型为一个发热电阻，结构十分简单，耦合因素很少，因此还需要寻找更适合光机载荷热控模型修正的软件。为与当前仿真软件更好地适配，优化平台需要与仿真软件有良好的接口，除此之外，在光机载荷热控模型修正领域中，还需要流程简洁、算法丰富、方便二次开发和代理模型计算功能。表6 中总结了目前航天热分析的常用软件，表7 介绍了可以用于热模型修正的多学科优化软件的优劣，两者结合分析，得到两类软件对于解决光机载荷模型修正问题的适用性。

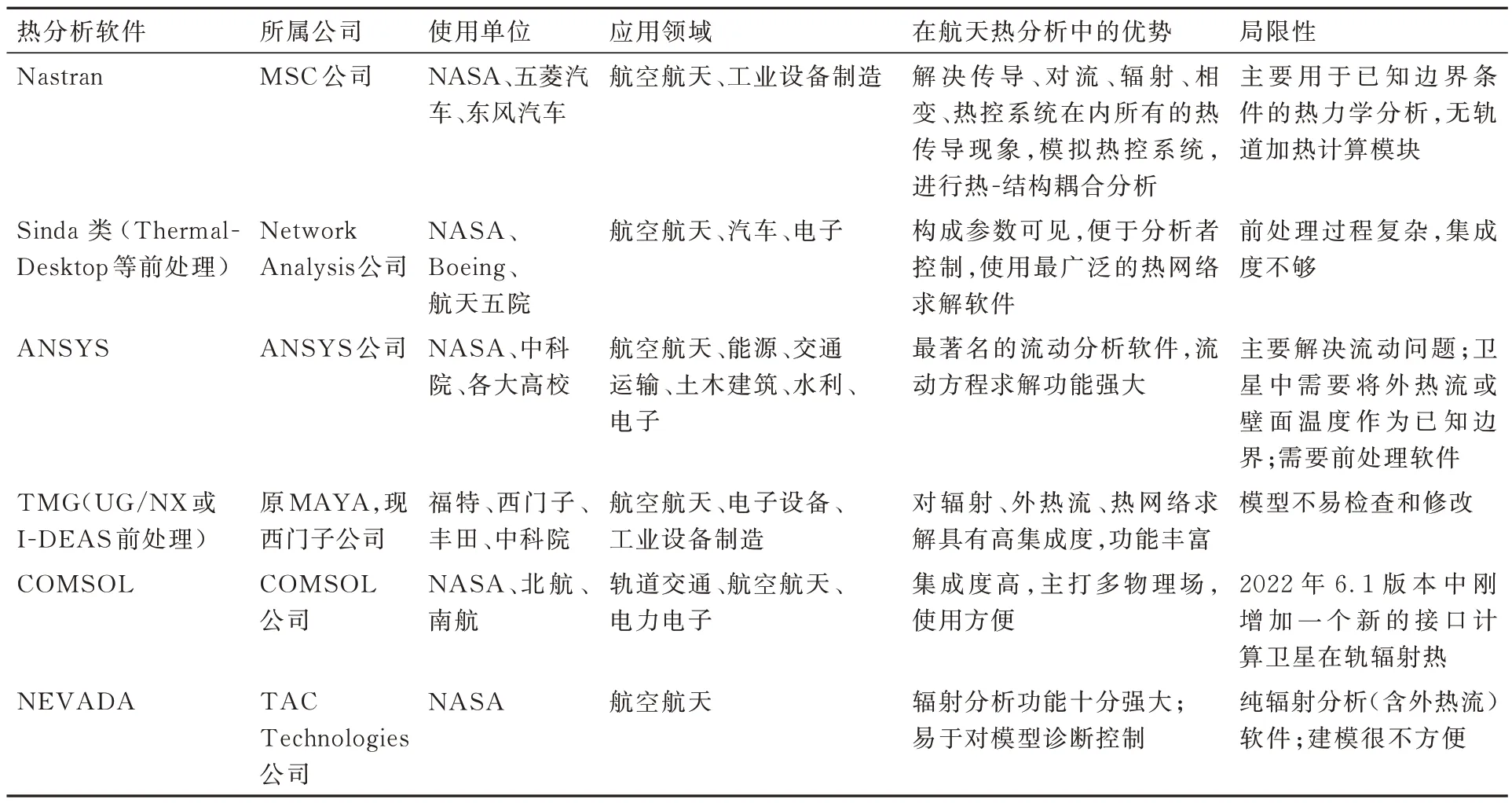
表6 航天热分析常用软件Table 6 Common software for aerospace thermal analysis

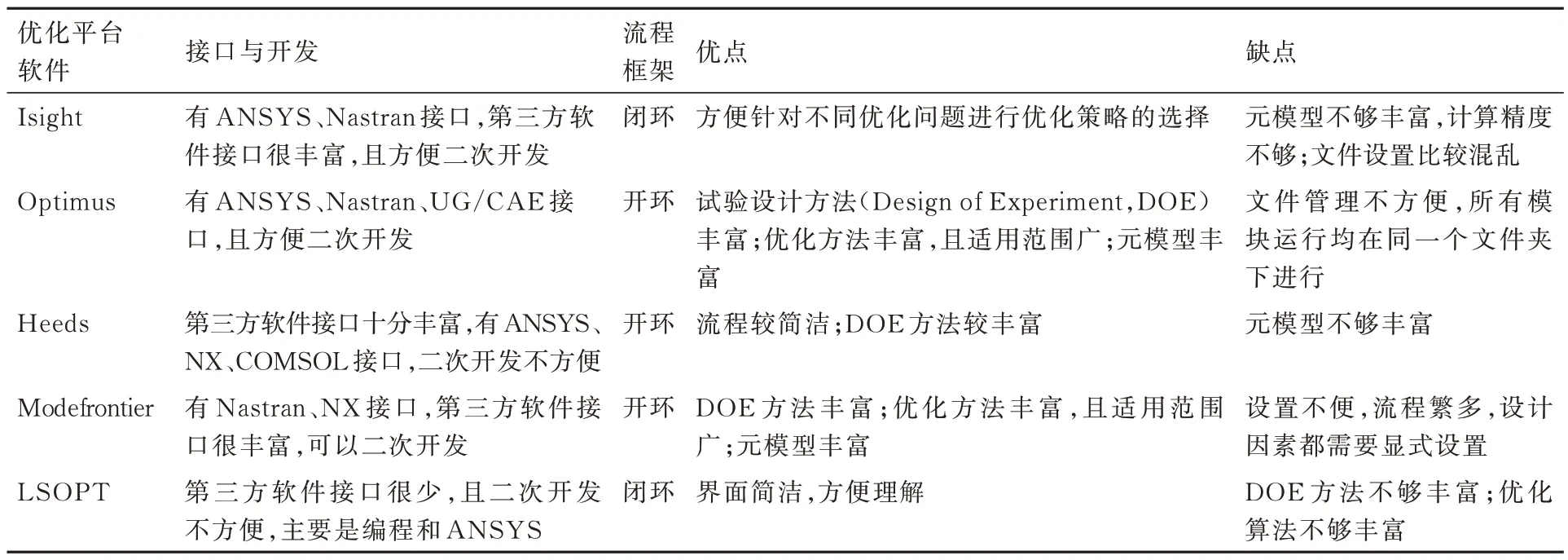
表7 多学科优化软件对比Table 7 Comparison of multidisciplinary optimization software

以Optimus 为例简要介绍这类优化软件的实现原理。这类优化软件的底层逻辑是通过一个个.bat 批处理文件调用相应的不同软件实现若干的功能，许多基础功能已经形成了用户友好型界面，并能够自动循环，不再需要热设计工程师人工编程实现，因此更利于工程上广泛应用。热模型修正问题的典型工作流如图10 所示，依次包含输入参数、运行宏文件、运行仿真软件、导出仿真结果、输出参数统计和目标函数寻优，其中也可以选择不同的代理模型和寻优算法。可以看出，该工作流可以实现经典蒙特卡洛法基本步骤和各种的算法改进，只需要一定的与特定问题相适配的宏文件录制和参数关联。

图10 Optimus 典型工作流Fig.10 Typical workflow of Optimus

光机载荷热控系统主要依赖于辐射和导热进行控温，其仿真软件需要有以下需求：①有轨道加热模块直接计算外热流；②对辐射和导热的计算精度要求较高，而对流传热计算则要求不高；③便于与其他优化软件进行集成。实际工程中需要基于上述分析选择合适的仿真软件，并建议与多学科优化软件平台组合使用。

在本节中，介绍了提高热模型修正效率的最后一种方法——利用自动修正工具代替人为操作，集成修正流程。首先分别综述了当前热模型修正领域和其他领域中已经研发的自动化修正优化工具，发现了当前优化工具普遍存在无法广泛工程化应用的问题，于是提出了将仿真软件与优化软件结合使用的方法，对热仿真模型修正的流程进行了规范化，通过这种方式可以提高用户使用友好性，介绍了当前各热仿真软件的优劣和适用性，各优化软件与热仿真软件的接口和优劣。

5 总结及展望

经过多年的发展积累，国内外热分析模型修正的方法越来越多样化，随着计算机能力的提升和人工智能的飞速发展，基于机器学习的方法逐渐被引入修正过程。本文首先介绍了近年关于航天器热模型修正的一般方法。然后基于卫星光机载荷热模型修正对于瞬态、精确、高效的要求，总结了卫星光机载荷热模型修正的研究进展。由于高效的重要性，重点分析了寻优算法、代理模型和自动修正工具这3 种提高热模型修正效率的新方法。介绍了前2 种方法的研究进展和各自方法的适用性和局限性，分析了几种有限元仿真软件和优化平台软件各自的优劣，并讨论了集成使用的可能性。

但上述新模型新方法仍有一定缺陷，距离工程应用也还有一定距离。因此，从以下几点做出展望：

1）参考其他类似领域中解决问题的思路，合理引入新型寻优算法和机器学习的方法，解决光机载荷热模型高效修正的问题。

2）基于现有的热仿真商业软件和优化软件开发优化新的集成优化平台，将代理模型、寻优算法等新方法集成在一个用户友好型页面，以便实现广泛的工程应用，形成参数修正与优化过程集成化自动化，简化修正流程，进一步提高修正效率。

3）深入研究参数分布规律，确定更为合理精确的参数分布，尽量完整地使用参数的分布还有其他宝贵信息。

4）根据不同边界条件（如温度等）对参数进行多次修正，得到的结果形成参数库，为热设计提供更准确的参数，减少对修正的依赖。