基于背景间运算的部分已知概念构造
田雪 任睿思

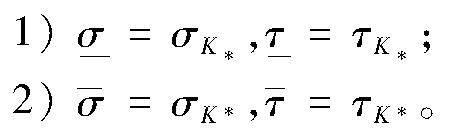

摘要 概念是利用形式概念分析进行知识获取的基础。在不完备形式背景中,为了表达“一定具有”以及“可能具有”的关系,概念的外延或内涵通常以区间集的形式表达,称这样的概念为部分已知概念。由部分已知概念的定义可知,其本质与不完备背景的最小和最大完备化有关,因而考虑对最小和最大完备化背景进行运算来寻找部分已知概念。通过将不完备形式背景的最小完备化与最大完备化分别进行并置和叠置构造两个新背景,其概念格分别同构于SE-ISI概念格和ISE-SI概念格,从而提出了构建SE-ISI概念格和ISE-SI概念格的新方法。对于ISE-ISI概念,使用不完备形式背景的最小与最大完备化的直和运算构造了新的形式背景,基于此背景提出了寻找ISE-ISI概念的方法。
关键词 不完备形式背景;部分已知概念;并置;叠置;直和
Construction of partially-known formal concepts basedon operations of formal contexts
Abstract Concepts are the foundation for knowledge acquisition through formal concept analysis. In incomplete formal contexts, in order to express “jointly must possessing (possessed)” and “jointly might possessing (possessed)”relationships, the extent or intent of concepts is usually expressed in the form of interval set. We refer to such concepts as partially-known formal concepts. From the definition of partially-known formal concepts, it can be seen that their essence is related to the least and greatest completions of incomplete formal contexts. Therefore, we consider performing operations on the least and greatest completions of incomplete formal contexts to find partially-known formal concepts. We construct two new formal contexts based on the apposition and subposition of the least and greatest completions. Their concept lattices are isomorphic to the SE-ISI concept lattice and the ISE-SI concept lattice, respectively. Therefore, the new methods for constructing SE-ISI concept lattice and ISE-SI concept lattice are proposed. For the ISE-ISI concept, we use direct sum operation of the least and greatest completions to construct a new formal context, and propose a method to search for the ISE-ISI concepts.
Keywords incomplete formal context; partially-known formal concept; apposition; subposition; direct sum
德國数学家Wille提出的形式概念分析(formal concept analysis, FCA)[1]是进行数据库知识发现的重要工具。通过在背景上获取概念及其对应的概念格结构,可以进行属性约简[2-3],规则获取[4]等研究,从而获取有用的知识。近年来,FCA与其他理论的融合研究[5-8]为基于形式概念的知识获取提供了更加丰富的理论支撑。
经典的形式背景包含了原始数据的所有信息,其上的知识是确定且完备的,在此基础上容易建立结构清晰的概念格,研究知识获取问题相对容易,但在数据不完整的情况下,研究相应问题就比较困难了。在不完备形式背景中,任一对象和属性间的关系有3种可能的情况:确定具有、确定不具有和不确定是否具有。因此,不完备背景中概念的定义、表达方式与完备背景中的概念有很大差异。
形式背景是一种理想状态下的数据表现,但在现实生活中由于数据获取较困难、记录不当等原因,往往存在数据缺失的情况,部分对象和属性之间的关系无法确定,从而导致形式背景的不完备性。在这种情况下,若简单地将缺失信息进行删除或补全,势必会导致知识获取的不确定性。因此,从不完备背景本身出发,对区间集形式的部分已知概念进行研究是有意义的。
Burmeister和Holzer受可能世界理论的启发提出了不完备形式背景,并且将模态算子引入不完备形式背景中[9]。Djouadi等从不完备背景的最小和最大完备化出发,提出了ill-known形式概念[10]。Li等提出了近似概念,其外延是一个对象集,内涵是一对属性集,并证明了一个不完备背景的所有近似概念形成一个完备格[11]。Li和Wang将三支决策应用到不完备背景中,并研究了属性约简问题[12]。Yao将区间集理论引入到不完备形式背景中,定义了3类部分已知概念:SE-ISI概念、ISE-SI概念和ISE-ISI概念[13]。Ren等进一步研究了部分已知概念的结构[14]。Zhi等考虑了不具有关系,对部分已知概念进行了扩展[15]。对于部分已知概念的研究目前主要集中在对其定义、性质以及结构的讨论,并未探讨其构造问题,本文通过考虑背景间的运算研究了部分已知概念的构造。
在三支概念分析领域,Qian等提出了基于背景的并置和叠置构造三支概念格的新方法[16]。受此启发,本文将其应用到不完备背景中寻找部分已知概念。由于不完备形式背景可以被等价刻画为一个下界和上界分别为最小完备化以及最大完备化的区间集,而部分已知概念的获取算子与最小完备化和最大完备化上的经典导出算子之间具有一致性,所以通过对最小完备化与最大完备化使用不同的放置方式构造新的形式背景,在新背景上构造经典形式概念,即可获取部分已知概念。
本文首先给出了不完备背景上部分已知概念的基础知识,然后通过将不完备背景的最小完备化与最大完备化进行并置和叠置构造新的背景,并证明了此背景下的经典形式概念格分别与SE-ISI概念格和ISE-SI概念格同构,从而提出了构建SE-ISI概念格和ISE-SI概念格的方法。对于ISE-ISI概念,通过将不完备背景的最小和最大完备化进行直和运算构造了新的形式背景,基于此背景提出了构造ISE-ISI概念的方法。最后,总结了文章的内容并提出了未来可以进一步研究的问题与方向。
1 预备知识
本节给出形式概念分析、不完备形式背景及其上部分已知概念的基础知识。
定义1[17] 称K=(OB,AT,I)为一个形式背景。其中:OB={o1,o2,…,op}为对象集,每个oi (i≤p)称为一个对象;AT={a1,a2,…,aq}为属性集,每个aj (j≤q)称为一个属性;I为OB和AT之间的二元关系,IOB×AT。若(o,a)∈I,则表示对象o具有属性a,记为oIa。
其中:σ(O)表示O中所有对象共同具有的属性集合;τ(A)表示共同具有A中所有属性的对象集合。如果一个二元组(O,A)满足σ(O)=A,且τ(A)=O,则称(O,A)是一个形式概念,简称概念。O和A分别称为概念(O,A)的外延和内涵。
在形式背景K=(OB,AT,I)的所有概念构成的集合上定义偏序关系和上、下确界就可以形成一个完备格,称之为形式背景K的概念格,记为L(K)。
(o,a,+)∈J表示对象o具有属性a;
(o,a,-)∈J表示对象o不具有属性a;
(o,a,?)∈J表示不确定对象o是否具有属性a。
一个完备的形式背景可以看作不完备背景的特殊情况,即完备背景中不含有“?”关系。
例1 表1为一个不完备形式背景IK=(OB,AT,{+,?,-},J)。其中:OB={1,2,3,4}为对象集;AT={a,b,c,d,e}表示属性集。表中(1,a)处的“+”表示对象1具有属性a;(1,b)位置上的“-”表示对象1不具有属性b;(1,c)处的“?”表示不确定对象1是否具有属性c。若将其中的“?”全部替换为“+”或“-”,表1就变成了一个完备背景。
在不完备背景中,无法通过常规导出算子实现对象集和属性集之间的推导,于是有了上界导出算子和下界导出算子的定义。
定义4[9] 设IK=(OB,AT,{+,?,-},J)是一个不完备背景,K=(OB,AT,I)是一个完备背景,若I满足下列条件:
则称K为IK的一个完备化。
由定义4可知,完备化背景中的二元关系I可以通过将不完备背景中的每个“?”替换为“+”或“-”得到。一个不完备形式背景具有多种完备化结果,可以用COMP(IK)表示不完备背景IK的所有完备化的集合。在不完备背景的多种完备化背景中,有两个背景较为特殊,下面给出了最小和最大完备化的定义。
定义5[10] 给定一个不完备形式背景IK=(OB,AT,{+,?,-},J),其最小完备化和最大完备化分别定义如下:
K*=(OB,AT,I* );K*=(OB,AT,I* )。
其中:I*={(o,a)|(o,a,+)∈J};I*={(o,a)|(o,a,+)∈J}∪{(o,a)|(o,a,?)∈J}。
例2 表2和表3分别是表1所示背景对应的最小完备化K*与最大完备化K*。可以看出,二元关系I*实际上是将所有“?”替换为“-”得到的,I*是将所有“?”换为“+”得到的。
令UP={(o,a)|(o, a, ?)∈J}表示不完
下面的定理给出了不完备形式背景中的上、下界导出算子与最小完备化和最大完备化中的导出算子之间的关系。
定理1[13] 在不完备背景中,有
其中:(σK*,τK*)是最小完备化K*=(OB,AT,I*)上的导出算子对;(σK*,τK*)是最大完备化K*=(OB,AT,I*)上的导出算子对。
该定理表明,下界导出算子和上界导出算子分别是最小完备化和最大完备化上的导出算子。因此,上、下界导出算子具有常规导出算子的所有性质。
使用上述两个算子可以实现从集合到区间集的转换,即将对象集映射为属性区间集,将属性集映射为对象区间集。而下面定义的两个算子可以将一个对象区间集映射为一个属性集,将一个属性区间集映射为一个对象集。
则被称为具有外延区间集和内涵集的部分已知形式概念,简称为部分已知ISE-SI形式概念。
在给出部分已知概念格的偏序关系及其上、下确界的定义之前,先说明区间集中偏序关系和交、并运算是如何定义的。给定两个区间集[A,B]和[C,D],偏序关系定义为
交运算和并运算分别定义为
[A,B]∩[C,D]=[A∩C,B∩D],
[A,B]∪[C,D]=[A∪C,B∪D]。
記IK上所有的SE-ISI概念形成的偏序集为LSE-ISI(IK),是一个完备格,其中偏序关系定义为
下确界和上确界分别定义为
记IK上所有的ISE-SI概念形成的偏序集为LISE-SI(IK),它是一个完备格,其中偏序关系定义为
下确界和上确界分别定义为
([X1,X2],Y)∧([U1,U2],V)=
([X1,X2]∩[U1,U2],
定理3[10] 在不完备形式背景中,如果一对对象区间集和属性区间集([O*,O*],[A*,A*])满足如下条件:
2) (O*,A*)是K*=(OB,AT,I*)中的一个形式概念,即σK*(O*)=A*,τK*(A*)=O*;
3) (O*,A*)是K*=(OB,AT,I*)中的一个形式概念,即σK*(O*)=A*,τK*(A*)=O*,
则称([O*,O*],[A*,A*])为一个部分已知ISE-ISI概念。
该定理是对ISE-ISI概念的构造性解释,即一个ISE-ISI概念由两个形式概念组成,这两个概念分别来自最小完备化K*和最大完备化K*。
记IK上所有的ISE-ISI概念形成的偏序集为LISE-ISI(IK)是一个完备格,其中偏序关系定义为
下确界和上确界分别定义为
例3 (续例1)对于表1表示的不完备形式背景IK,可以根据定义7和定理3寻找其上的3类部分已知概念。如令O={1,3},则
故(13,[a,ac])是一个SE-ISI概念。
类似地,取A={a,c},则
故([3,13],ac)是一个ISE-SI概念。
2 基于背景的并置构造SE-ISI概念格
本节将通过不完备背景的最小完备化与最大完备化的并置构造具有与SE-ISI概念格同构的概念格的形式背景,进而使用构造概念格的经典方法构造SE-ISI概念格。
定义8[17] 设K=(OB,AT,I),K1=(OB1,AT1,I1),K2=(OB2,AT2,I2)是形式背景。记OB′j={j}×OBj,AT′j={j}×ATj及I′j={((j,o),(j,a))|(o,a)∈Ij}。其中,j∈{1,2}。若OB=OB1=OB2,则K1|K2=(OB,AT′1 ∪AT′2,I′1 ∪I′2 )称为K1与K2的并置。一般地,若OB=OB1=OB2,且AT1∩AT2=,则K1|K2=(OB,AT1∪AT2,I1∪I2)也称为K1与K2的并置。
下面将K*和K*并置构造一个新的形式背景,基于新的形式背景建立SE-ISI概念格。
设不完备背景IK=(OB,AT,{+,?,-},J)的最小和最大完备化分别为K*=(OB,AT,I*)和K*=(OB,AT,I*),为了区分两个背景上的属性,现对K*和K*中的属性集分别添加标签{1}和标签{2},定义两个新的形式背景。
定理4 假设K*和K*分别为不完备形式背
证明 对任意(O,A)∈L(K0),定义φ(O,A)=(O,[A1,A2])。其中:A1={x|(1,x)∈A};A2={x|(2,x)∈A}。下证φ是L(K0)与LSE-ISI(IK)间的同构映射。
1)证明φ是一个映射,即证对任意的(O,A)∈L(K0),都有φ(O,A)=(O,[A1,A2])∈LSE-ISI(IK)。
综上可知,(O,[A1,A2])∈LSE-ISI(IK),即φ:L(K0)→LSE-ISI(IK)是映射。
2)证明φ是双射,即证φ既是单射又是满射。首先,对于任意的(X,Y),(U,V)∈L(K0)且(X,Y)≠(U,V),有X≠U,Y≠V。因而(X,[Y1,Y2])≠(U,[V1,V2]),即φ(X,Y)≠φ(U,V),因此,φ是单射。其次,证明φ是满射。即对任意的(O,[A1,A2])∈LSE-ISI(IK),定义A=({1}×A1)∪({2}×A2),有(O,A)∈L(K0),且φ(O,A)=(O,[A1,A2])。对于任意(m,n)∈A,分两种情况讨论。
a) (m,n)∈{1}×A1,即m=1,n∈A1。因为(O,[A1,A2])∈LSE-ISI(IK),故OI*=A1,OI*=A2,且O=AI*1 ∩AI*2,从而n∈OI*。因而对任意的o∈O,n∈oI*,由~的定义可知o~(1,n),由o的任意性可知(1,n)∈O~。
a) (m,n)=(1,n),由~的定义知n∈oI*,由o的任意性知n∈OI*,又因为OI*=A1,故n∈A1,因而(m,n)=(1,n)∈{1}×A1A。
b) (m,n)=(2,n),同理有(2,n)∈A。
综上所述,L(K0)与LSE-ISI(IK)同构。
由定理4可以得到定理5,该定理提出了一种寻找SE-ISI部分已知概念的方法。
例4 表1所示不完备形式背景所对应的最小完备化K*,最大完备化K*,带属性标签的最小完备化*,带属性标签的最大完备化*, 以及其并置K0, 分别如表2~6所示,图1为K0的概念格。 以概念C∈L(K0)为例来解释定理5, 由于C=(13,{(1,a),(2,a),(2,c)})∈L(K0),所以有O={1,3},A1={a},A2={a,c},于是概念C所对应的SE-ISI概念为(13,[a,ac])。通过对L(K0)中所有概念进行转换,就可以得到不完备背景IK的SE-ISI概念格,如图2所示。
3 基于背景的叠置构造ISE-SI概念格
與第2节类似,本节将不完备背景的最小完备化与最大完备化进行叠置来构造具有与ISE-SI概念格同构的概念格的形式背景,基于新形式背景使用构造经典概念格的方法构造ISE-SI概念格。
下面将K*和K*进行叠置得到新的形式背景,基于新的形式背景建立ISE-SI概念格。
设不完备背景IK=(OB,AT,{+,?,-},J)的最小和最大完备化分别为K*=(OB,AT,I*)和K*=(OB,AT,I*)。为了区分两个背景上的对象,现对K*和K*中的对象集分别添加标签{1}和标签{2},定义如下两个新的形式背景。
證明 由于对象集与属性集之间是对偶的,与第2节证明同理,此处略去。
例5 表7是不完备背景IK所对应的叠置背景K1,图3为K1的概念格L(K1),以概念F为例解释定理7。由于F=({(1,3),(2,1),(2,3)},ac)∈L(K1),因而O1={3},O2={1,3},A={a,c},于是可以得到概念F所对应的ISE-SI概念为([3,13],ac)。通过转换L(K1)的所有概念,就可以得到IK的ISE-SI概念格,如图4所示。
4 基于背景的直和构造ISE-ISI概念格
本节通过对不完备形式背景IK的最小完备化与最大完备化进行直和运算构造新的背景,从而获取ISE-ISI概念。
定义10[17] 设K=(OB, AT, I), K1=(OB1, AT1, I1), K2=(OB2,AT2,I2)是形式背景。记OB′j={j}×OBj,AT′j={j}×ATj及I′j={((j,o),(j,a))|(o, a)∈Ij}。 其中, j∈{1, 2}。 则称K1+K2=(OB′1∪OB′2, AT′1∪AT′2, I′1∪I′2∪(OB′1×AT′2)∪(OB′2×AT′1))为K1与K2的直和。
定理8给出了如何利用不完备背景的最小完备化与最大完备化的直和构造新背景并获取ISE-ISI概念。在直和运算中,为了区分K*和K*上的对象和属性,对两者的对象集和属性集分别添加标签{1}和标签{2}。
2)类似地,可以证明A2=OI*2,O2=AI*2。
综上所述,([O1,O2],[A1,A2])是一个ISE-ISI部分已知概念。
5 结语
本文基于形式背景的并置、叠置及直和运算,提出了构造SE-ISI概念格、ISE-SI概念格以及寻找ISE-ISI概念的方法。对于一个形式背景,通过将其最小和最大完备化并置得到一个新的形式背景K0,该背景的经典概念格同构于SE-ISI概念格,对L(K0)中每个概念进行一定的转换,就可以得到SE-ISI概念格。对偶地,通过将不完备背景的最小和最大完备化叠置,使用经典概念格的构造方法就可以得到ISE-SI概念格。对于ISE-ISI概念,使用背景的直和运算构造了新的形式背景,当该背景中的概念满足一定条件时,它的概念就可以转换为ISE-ISI概念。
从定义出发构造部分已知概念涉及到集合与区间集的相互转换,构造较为复杂,但由部分已知概念的定义可知,其本质与不完备背景的最小和最大完备化有关。因此,考虑从最小和最大完备化出发,使用不同的放置方式构造新背景来获取部分已知概念。该方法可以将不完备背景上的部分已知概念与完备背景上的形式概念联系起来,而形式概念的构造已有很丰富的研究成果,这些成果可以指导部分已知概念的构造与获取。本文虽然通过背景的直和运算将完备背景中的形式概念与不完备背景中的ISE-ISI概念进行了联系,但是这两种概念格之间并没有建立同构映射,即通过背景直和获取的经典概念必须在满足一定条件的情况下才能被转化为ISE-ISI概念。所以在未来的研究中,将继续深入探究不完备背景下的ISE-ISI概念与经典概念之间的关系,寻找更加有效且直观的ISE-ISI概念构造方法。
参考文献
[1] WILLE R. Restructuring lattice theory: An approach based on hierarchies of concepts [C]∥RIVAL I. Ordered Sets. Dordrecht-Boston: Reidel, 1982: 445-470.
[2] QIN K Y, LIN H, JIANG Y T. Local attribute reductions of formal contexts[J]. International Journal of Machine Learning and Cybernetics, 2020, 11(1): 81-93.
[3] 张文修, 魏玲, 祁建军. 概念格的属性约简理论与方法[J]. 中国科学E辑:信息科学,2005,35(6):628-639.
ZHANG W X, WEI L, QI J J. Attribute reduction theory and approach to concept lattice[J]. Science in China Series F: Information Sciences, 2005, 48(6): 713-726.
[4] WEI L, LIU L, QI J J, et al. Rules acquisition of formal decision contexts based on three-way concept lattices [J]. Information Sciences, 2020, 516: 529-544.
[5] GUO L K, HUANG F P, LI Q G, et al. Power contexts and their concept lattices[J]. Discrete Mathematics, 2011, 311(18/19): 2049-2063.
[6] KENT R E. Rough concept analysis: A synthesis of rough sets and formal concept analysis[J].Fundamenta Informaticae, 1996,27(2):169-181.
[7] QI J J, WEI L, YAO Y Y. Three-way formal concept analysis[C]∥Proceedings of Rough Sets and Knowledge Technology. Shanghai: Springer, 2014: 732-741.
[8] QI J J, QIAN T, WEI L.The connections between three-way and classical concept lattices[J]. Knowledge-Based Systems, 2016, 91: 143-151.
[9] BURMEISTER P, HOLZER R. On the treatment of incomplete knowledge in formal concept analysis[C]∥Conceptual Structures: Logical, Linguistic, and Computational Issues. Berlin: Springer-Verlag, 2000: 385-398.
[10]DJOUADI Y, DUBOIS D, PRADE H. Différentes extensions floues de l′analyse formelle de concepts[J]. Actes Renc Franc Sur la Logique Floue et ses Applications Cépadues Edn, 2009: 141-148.
[11]LI J H, MEI C L, LV Y J. Incomplete decision contexts: Approximate concept construction, rule acquisition and knowledge reduction[J]. International Journal of Approximate Reasoning, 2013, 54(1): 149-165.
[12]LI M Z, WANG G Y. Approximate concept construction with three-way decisions and attribute reduction in incomplete contexts[J]. Knowledge-Based Systems, 2016, 91: 165-178.
[13]YAO Y Y. Interval sets and three-way concept analysis in incomplete contexts[J]. International Journal of Machine Learning and Cybernetics, 2017, 8(1): 3-20.
[14]REN R S, WEI L, YAO Y Y. An analysis of three types of partially-known formal concepts[J]. International Journal of Machine Learning and Cybernetics, 2018, 9: 1767-1783.
[15]ZHI H L, CHAO H. Three-way concept analysis for incomplete formal contexts[J]. Mathematical Problems in Engineering, 2018, 2018:1-11.
[16]QIAN T, WEI L, QI J J. Constructing three-way concept lattices based on apposition and subposition of formal contexts[J]. Knowledge-Based Systems, 2017, 116: 39-48.
[17]GANTER B, WILLE R. Formal concept analysis: Mathematical foundations[M].New York: Springer, 1999.

