基于多源数据融合的抽水蓄能项目投资估算方法
陈菲菲
(广东省水利电力勘测设计研究院有限公司,广东 广州 510610)
抽水蓄能电站的总进度工期设计需要充分考虑电站的建设条件、工程规模、技术特点等因素,项目的建设工期是指预可研、电站设计期、筹建期、主体工程建设期、竣工决算期。其中工程筹建期之前受外部条件影响较大,时间成本相对不确定[1]。工程完建期主要进行项目竣工决算工作。主体工程建设周期一般为8年左右,当项目进入主体工程建设阶段,抽水蓄能电站的设计图已完成,概算总额已确定,建设任务基本确定。
国家能源局批准的选点规划报告是开展项目前期工作及核准建设的基本依据。在可行性研究阶段,要根据预可行性研究阶段等相关材料进行抽水蓄能电站建设的设计工作;在电站设计期,设计院出具电站的设计图和施工图;在筹建期基建部与工作人员开展项目建设招标、设备采购计划等工作;在主体工程建设期,项目的建设周期、工作计划基本确定,开始进行水库、洞室等主体工程的建设以及设备的采购;当所有机组达到可使用状态后[3],项目进入竣工决算期,在此期间,需要完成项目的决算工作并制定尾工建设计划[4]。受地理位置、交通、气候、地方政策的影响,不同的抽水蓄能电站在主体工程建设期前所需的时间不确定。在综合考虑技术难度、工程建设环境、物资供应及移民征地等各方面因素,确定总工期。对此,本文提出基于多源数据融合的抽水蓄能项目投资估算方法。
1 抽水蓄能项目投资估算的影响因素
目前,在这样的市场现状下,影响抽水蓄能项目投资估算的因素种类繁多[5],从整体上来说大致可分为两类。
1.1 宏观因素
宏观因素主要是指由国家的整体经济形势和其它各方面所造成的,企业无法控制的影响投资估算的因素。
(1)国家物价消费指数以及各个时期的基准利率和还贷款利息,它们主要影响投资估算的贷款规模及压力。
(2)项目造价指数,它是反映不同时期项目造价相对变化趋势的一种指标,是项目动态结算的重要依据。
(3)国家关于项目投资管理相关法律法规的颁布及修改,如建设部标准定额司推行的工程量清单计价模式会极大地影响投资估算的风险考虑成度。
1.2 微观因素
微观因素主要指企业能够控制的,并可以通过努力消除其对抽水蓄能项目投资估算影响的因素。
(1)抽水蓄能项目的设计深度。它是影响抽水蓄能项目投资估算的一项非常重要的内容。如果抽水蓄能项目只是以一种意向的状态而存在,还没有相应的初步规划设计方案图纸或草图,那么编制投资估算就会变得很困难,所以,具有一定深度的规划设计方案是保证投资估算准确度的可靠保障。
(2)从事编制抽水蓄能项目投资估算人员的自身业务素质和经验。
2 抽水蓄能项目投资多源数据融合
数据融合算法是整个融合过程中的核心,无论是什么数据类型最终都是需要经过某种算法的融合处理[6]。由于数据融合是一门交叉学科,所涉及的研究领域广泛,因此针对不同研究场景存在着不同的融合方法。实际应用中还不存在能够解决所有场景问题的算法,必须针对不同应用场景选择合适的方法[7]。本文采用长短时记忆神经网络算法进行抽水蓄能项目投资多源数据融合,神经网络结构图如图1所示。

图1 LSTM神经网络结构图
由图1可知,LSTM神经网络结构共有遗忘门、输入门、输出门3种门控结构,其中h代表隐含层状态,C为单元状态,x为输入的抽水蓄能项目投资数据。
用遗忘门的输出值控制上时刻单元状态被遗忘的程度。值为0表示完全遗忘,值为1表示完全保留。遗忘门的计算公式如下:
ft=sigmoid(Wf·[ht-1,xt]+bf)
(1)
式中,Wf、bf—遗忘门的权重和偏置。
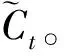
it=sigmoid(Wi·[ht-1,xt]+bi)
(2)
(3)
(4)
式中,Wi、Wc和bi、bc—权重和偏置;Ct—更新后的当前单元状态。
输出庅主要控制当前单元状态有多少会被保存到当前输出中,即抽水蓄能项目投资数据融合存储量的多少。结合输出门的输出ot和当前单元状态Ct,确定最终输入到下一个记忆单元的隐层输出ht。输出门及隐层输出(即数据融合)计算公式如下:
ot=sigmoid(W0·[ht-1,xt]+b0)
(5)
ht=ot*tanh(Ct)
(6)
式中,W0、b0分—权重和偏置。基于上述数据融合结果进行抽水蓄能项目投资估算。
3 算法流程
通过将抽水蓄能项目投资有影响的宏观因素和微观因素作为多源数据融合信息输入到模型作为变量,把要估算的抽水蓄能项目投资作为模型的输出,通过平均影响值算法和粒子群算法确定最优的支持向量机模型来对抽水蓄能项目投资进行估算。该算法主要操作详解如下:
(1)将搜集到的样本数据集输入至SVM网络中进行训练;
(2)将样本中第i个敏感性特征指标数据分别加减10%,而其余的指标数据保持不变,构建的新样本记为P和Q;
(3)根据步骤(2),依次构建所有敏感性指标的新样本;
(4)以P和Q为例,采用SVM模型对样本进行模拟仿真,求得预测结果M和N;
(5)根据式(7)得到第i个敏感性特征指标对输出结果的影响程度;
(7)
(6)根据各敏感性特征指标MIV值的绝对值大小进行排序;
(7)按照依次MIV绝对值最小的原则构建新的敏感性特征指标体系,并且引入平均相对误差(MRE),计算每次剔除敏感性特征指标后的额平均相对误差;
(8)根据步骤(7)所得平均相对误差最小时,所对应的敏感性特征指标体系即最优指标体系;
(9)将上一步所选择的最优指标体系输入LSTM-SVM模型中进行模拟仿真;
(10)初始化粒子参数,包含:种群规模N,粒子飞行范围,确定惯性权重ω,选定终止条件和最大迭代数tmax,学习因子c1和c2,c和g的求值区间;
(11)按照f(x)计算每一代种群的误差值;
(12)判断误差值是否满足寻优终止条件或粒子更新是否达到参数设定的最大的迭代次数,如果达到,输出最优c和g;如果没有达到则继续下一步;
(13)根据公式(8)和公式(9)更新xi和vi;vi(t)=w·vi(t+1)+c1r1(pi-xi(t))+
c2r2(pg-xi(t))
(8)
xi(t+1)=xi(t)+vi(t)
(9)

(15)得到最优的SVM参数,并应用到模型进行抽水蓄能项目投资估算。
4 实验结果分析
4.1 数据收集与整理
通过广联达指标网收集了省内14个市抽水蓄能项目的投资数据,为了保证数据的时效性和真实性,本文剔除了2019年之前的投资数据,剩下近3年内50个抽水蓄能项目的投资数据。初步得到50组原始样本。
由于模型只能识别离散化的输入数据,所以需将部分原始数据样本进行量化处理,根据第1节确定的抽水蓄能项目影响因素的特点,将字符型的数据按照量化方式进行相应的赋值,以便模型的训练学习。
X1~X20作为输入指标,分别是:
(1)定量指标:总面积、地上面积、地下面积、建筑高度、层数、抗震设防烈度、钢筋市价、混凝土市价和人工市价共9个,分别记作:X1,X2,…,X9。
(2)定性指标:主体结构类型、基础类型、砌体材质、屋面防水材料、外墙材料、内墙材料、楼地面材料、门窗类型、强电设备安装水平、弱电及智能化设备安装水平和给排水设备安装水平共11个,分别记作X10,X11,…,X20。
4.2 结果分析
使用上述MATLAB训练好的神经网络进行预测,需要用到代码:Y=sim(net,X),将net视为映射关系,输入变量X即可得到Y。X的维度是20为估算的20个影响因素,Y的维度为1,是抽水蓄能项目的单方造价。得到的估算结果如图2和表1所示。

表1 投资估算精度分析
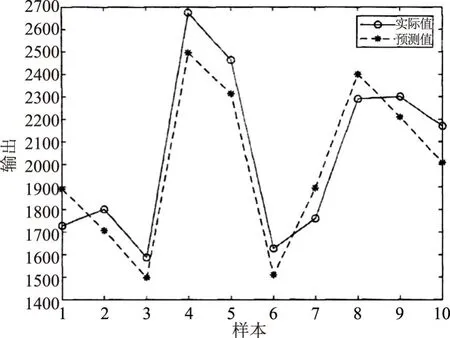
图2 投资实际值与估算值对比图
平均相对误差就是相对误差的平均值,而相对误差就是预测值与实际值之间的差再比上实际值,由于其正负符号问题,一般用平均相对误差的绝对值来表示,MRE的数学表达式如下:
(9)
得到投资估算精度及相对误差结果见表1。
由图2和表1可知:
(1)估算值和实际值的之间的关系,如图2所示,根据曲线的整体趋势可以看出,测试样本的计算结果和真实值较为贴近,说明基于BP神经网络模型进行投资估算的效果较好。
(2)估算值和实际值的对比差值用相对误差表,见表1,各组测试样本的估算值的相对误差均控制在10%以内,相对误差分布区间为[-9.37%,7.52%]之间,达到了抽水蓄能项目的投资初期对于估算的精度要求。
(3)从估算速度来看,从运行开始到绘图结束,总共花了4.01s。
5 结语
针对传统估算方法存在估算不准确、误差大的问题,提出基于多源数据融合的抽水蓄能项目投资估算方法。将抽水蓄能项目投资有影响的宏观因素和微观因素作为多源数据融合信息输入到模型作为变量,通过平均影响值算法和粒子群算法确定最优的支持向量机模型来对抽水蓄能项目投资进行估算。实验结果表明,采用本文方法可有效提高估算准确度,降低平均相对误差,具有一定的实用性。

