不同工艺参数对冰箱箱体发泡密度均匀性影响的仿真研究

王涛， 徐玉峰， 杜华东， 王金瑞， 陈新龙， 朱昭沂， 刘雅， 耿照梦

（1.澳柯玛股份有限公司， 山东 青岛 266100；2.山东科技大学 机械电子工程学院， 山东 青岛 266590）

0 引 言

在冰箱制造过程中，箱体注射量对冰箱发泡层的密度具有重要影响，注射量设置不同会导致冰箱发泡层整体密度的变化。过高或过低的密度都会导致产品出现质量问题，如挤压变形、漏泡等，且浪费材料和制造成本上升，因此合理设定箱体注射量对于冰箱发泡工艺至关重要。发泡料密度的均匀性是评估发泡质量的关键因素之一，发泡剂在箱体中的流动性对填充效果有显著影响，保持发泡剂的流动顺畅能够避免在发泡过程中出现空泡、泡孔粗糙和拉丝等质量问题。为了提升发泡质量及资源的利用率，工艺优化通常将降低密度极差和提高密度均匀性作为重要目标[1-2]。

目前，关于冰箱发泡的研究倾向于生产工艺方面。柯庆镝等[3]通过结合聚氨酯发泡的生产工艺过程，对基本机理进行了研究，探索了与发泡层结构相关的物理参数的演化规律，包括泡孔尺寸、泡孔密度、泡孔形状因子等，研究表明其物理参数对于发泡层结构的隔热性能和力学性能有重要影响；徐以国等[4]介绍了微孔发泡技术的历史发展、发泡原理、工艺流程以及泡孔控制等方面的内容，通过剖析这些关键要素，为相关领域的研究和实践提供了参考；廖玉松[5]从冰箱发泡模的实际设计和制造要求出发，对冰箱发泡模的关键结构进行了研究，探讨了冰箱发泡模箱体CAD∕CAM的实现方法，并设计了抽芯滑块机构。除此之外，冰箱发泡工艺还与型腔排气结构的位置和设计密切相关。李帅等[6]分析了发泡涨箱的主要原因，并指出通过型腔排出箱内的CO2及空气不通畅，会造成局部气压增高形成困气，对发泡料的流动产生一定的阻力，影响发泡质量。

然而，关于有限元仿真技术对发泡设计的研究还较少，通过运用仿真技术，分析发泡层密度不均匀的原因，可以实现对聚氨酯发泡过程中注射量的精确预测，有助于优化生产流程，提高冰箱质量，降低企业生产成本。因此，现借助有限元仿真技术进行分析，对聚氨酯发泡工艺的应用具有指导作用。

1 仿真模型搭建

1.1 物理模型搭建

研究对象为某单门无霜风冷冰箱，箱体尺寸为1 800 mm×600 mm×550 mm，发泡模具尺寸为2 000 mm×700 mm×700 mm，使用三维软件对箱体内的发泡层及模具建立几何模型。箱体内胆结构复杂，因此在模型结构突变部分进行了简化，图1所示为简化的箱体发泡层几何模型，图2所示为模具几何模型。

图1 箱体发泡层几何模型

图2 模具几何模型

在仿真软件中对几何模型进行网格划分，主要采用四面体网格，尺寸为5 mm，网格数量为1 500万个，模具初始温度为33～40 ℃，发泡剂初始温度为（21±3） ℃。

在实际生产过程中，注射喷嘴的相关参数对发泡成型具有重要的影响，主要包括喷嘴尺寸、流量速率以及移动路径等。对于喷嘴位置和数量，需要根据实际需求进行设定，以确保仿真结果的准确性和可靠性。现研究底部单喷嘴注射的情况，其中喷嘴位于压力机室的顶部，并由箱体底部向顶部方向进行注射，如图3所示。

图3 喷嘴注射点

1.2 数学模型搭建

冰箱箱体发泡的过程实际是泡沫在箱内逐渐膨胀并取代空气的过程，因此在模拟发泡料的注射及成型过程之前，需要先构建一个数学模型用以描述发泡剂在发泡过程中物理参数的变化曲线，其中密度、黏度和导热系数对于仿真模型的准确性具有重要的影响。对于箱内的泡沫膨胀，由于其复杂性，在进行数值计算模拟时进行如下假设：①当发泡剂完成发泡充型时，发泡层会立即固化；②在注射过程中，将发泡剂等效为湍流模型；③发泡料的膨胀速度不受料温和化学反应程度的影响。

1.2.1 密度公式

密度表示单位体积物质的质量，是物质的基本性质之一，对于聚氨酯泡沫，其数学模型是关于温度T、压力p、水分子转化效率X-W和发泡剂溶解度LGas的公式：

其中，xW.0为水组分的初始质量；Ll:q.0为溶解度的初始值；ρW为水的密度；ρPU为发泡剂的密度；ρRA.Liq为液态发泡剂的密度。

1.2.2 黏度公式

聚氨酯泡沫的黏度反映其在流动过程中的阻力，假设发泡剂中的气泡孔径足够小，则发泡剂可以近似为广义牛顿流体来进行数值模拟分析，黏度公式如下：

其中，μF表示表观黏度；φ表示气泡的体积分数；Ca表示毛细数。

1.2.3 热传导系数公式

热传导系数描述了聚氨酯泡沫在热量传递过程中的效率，根据与密度相关的经验公式获得，其表达式为：

其中，ρF表示聚氨酯泡沫的密度。

2 仿真分析结果

工艺上通常采用箱体发泡层的密度极差来评价发泡质量，密度极差越高，发泡料填充的不均匀性越明显，容易导致局部溢料、空泡、结皮及困气等工艺问题，影响冰箱的保温能力、能耗和强度。

基于此，通过分析成型后发泡料密度的分布趋势，可以了解箱体填充的均匀性，评估发泡工艺的质量，这有助于及时发现和解决潜在的问题，提高箱体成型质量和稳定性。

2.1 注射量预测分析

针对箱体结构，以总注射量为变量，注射量分别为5.70、5.85、6.00 kg，注射分布云图如图4所示，当注射量为5.70 kg时，由于单喷嘴底部注射，发泡剂仅流动到箱体后背区域的中心，出现分布不均匀的情况；而注射量为5.85 kg和6.00 kg，发泡剂流动分布相对较均匀。

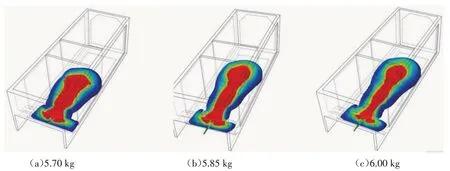
图4 注射分布云图

发泡密度分布云图如图5所示，当注射量分别为5.85 kg和6.00 kg时，发泡剂基本充满整个箱体，但在箱体右前下角和左前下角分别出现不同程度的困气现象，对发泡的流动性有一定的阻力，导致该区域有局部缺料的情况；当注射量为5.70 kg 时，发泡未充满整个箱体，由于注料分布不均匀（见图4（a）），导致在箱体顶端出现大量缺料的现象，说明充填量为5.70 kg时不满足工艺要求，3种不同注射量的最大密度、最小密度及极差值对比结果如表1所示。

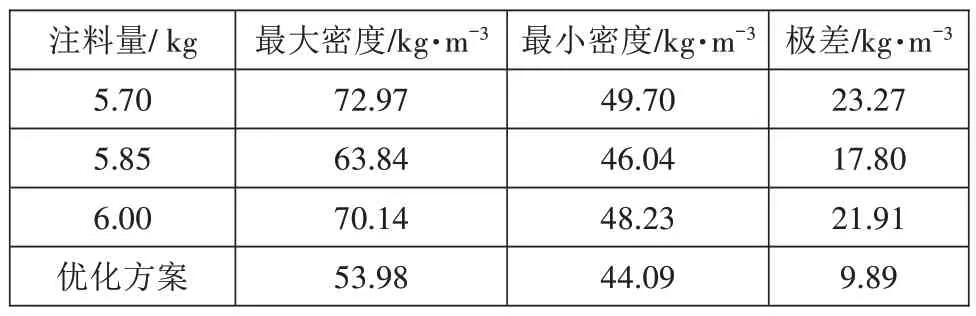
表1 密度分布结果

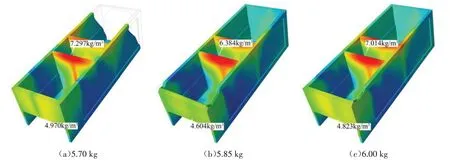
图5 发泡密度分布云图

充型过程中气压的分布云图如图6所示，注射量分别为5.70、5.85、6.00 kg，充填后均会产生不同程度的困气，最大气压值为10 MPa。由图6可见，困气位置基本落在箱体顶部、底部等发泡末端位置，在相应位置设置排气孔以消除缺陷。

图6 充型过程气压分布云图

2.2 优化仿真分析

通过仿真结果发现，随着注射喷嘴的尺寸增大，箱体密度方差呈现先减小后增大的趋势，如图7所示；由于注射速率不同，落料点分布也不同，对箱体密度方差的影响各有差异，如图8所示。对于该箱体，当注射量为5.85 kg时，使用注射内径R10 mm的喷嘴可以将箱体发泡层的密度方差降到最低，密度分布最均匀；与此同时，注射速率越大，密度分布越均匀。通过结果对比可以发现，使用喷嘴内径为R10 mm、注射速率为1.2 g∕s、注射量为5.85 kg时，计算结果见表1中优化方案，密度分布云图如图9所示，箱体发泡层的密度极差降低了50%，密度均匀性得到显著提升。除此之外，在图6所示的困气位置设置了相应的排气孔，最大气压为3.71 MPa，困气现象基本消除，优化方案气压分布云图如图10所示。

图7 喷嘴尺寸对密度分布的影响

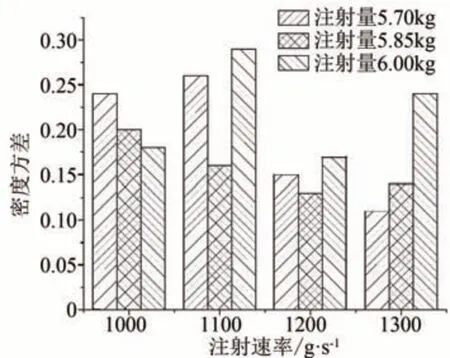
图8 注射速率对密度分布的影响

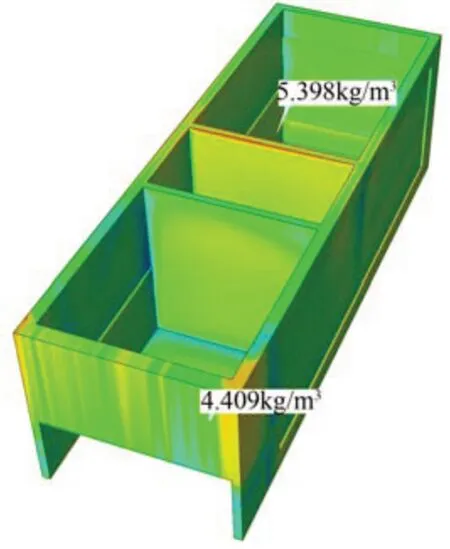
图9 优化方案密度分布云图

图10 优化方案气压分布云图

2.3 密度对标分析

以箱体后背上、下两部分为取样对象，通过排水法实际测得发泡层取样块的密度。试验测试结果如图11所示，上取样块实际测量密度为43.39 kg∕m³，仿真结果为45.06 kg∕m³；下取样块实际测量密度为42.43 kg∕m³，仿真结果为44.86 kg∕m³，仿真计算得到的结果与实测的密度值误差约为5%，符合程度较高。

图11 试验测试结果

3 结束语

运用仿真技术，分析不同工艺参数对冰箱发泡密度均匀性影响的研究方法是有效的，对仿真计算得到的结果与实测的密度值进行对标，结果一致性较高，证明了仿真的准确性和可靠性。

在此基础上，通过仿真技术可以灵活地调整工艺参数，并观察其对密度分布的影响。通过调整注射量、喷嘴尺寸、注射速率等工艺参数，可以找到最优的工艺条件，使箱体发泡后的密度均匀性得到大幅提高。

此外，仿真技术还可以在产品设计初期进行预测和优化，减少试制和测试的次数，缩短产品研发周期，降低研发成本。通过仿真技术的不断发展和完善，未来在冰箱发泡工艺以及其他材料加工领域的应用将会越来越广泛。