基于ADCP代表流速法“1+1”的多平台流量测验比测研究

张丹凤，王文娟，尤家伟，吴云浩，饶勇

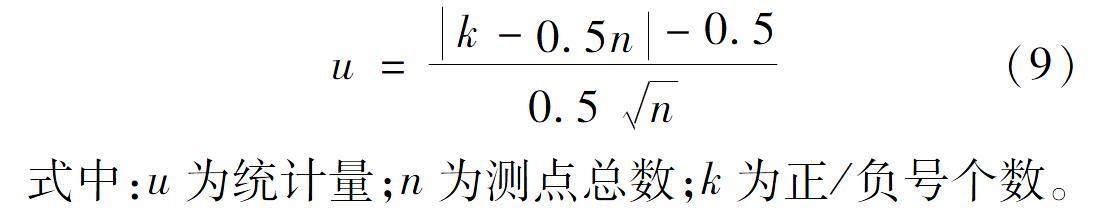
摘要：为提高回水项托河段流量测验精度，有力支撑巡测管理，提出了基于ADCP代表流速法“1+1”的多平台流量测验方法，并在汉江中游干流控制站余家湖水文站进行了应用。“1+1”表示水平式ADCP（H-ADCP）和垂直式ADCP（V-ADCP）方法，即通过收集走航式ADCP实测流量成果与同时段H-ADCP、V-ADCP的测验成果，建立实测断面平均流速与H-ADCP代表流速以及V-ADCP代表流速的相关关系。通过比较不同回归方程的计算精度，确定最优回归方程，并对相关关系定线精度进行检验。结果表明：符号检验、适线检验、偏离检验的结果分别为0.45，0.61和0.34，相关关系定线精度符合规范规定要求，说明基于ADCP代表流速法“1+1”的多平台流量测验方法在余家湖水文站的适用性良好，具有一定的推广价值。

关键词：流量测验； ADCP； 代表流速法； 回归分析； 余家湖水文站

中图法分类号：P332.4                    文献标志码：A                   DOI：10.15974/j.cnki.slsdkb.2024.03.004

文章编号：1006-0081（2024）03-0023-07

0引言

在水文观测领域，河流流量测验一直是水文监测领域研究的重要内容。传统的流速流量测验需要耗费大量的人力物力，且实时性差，准确度低，难以满足科研和生产的需要。随着水声技术的不断进步，在 20 世纪 80 年代初，声学多普勒流速剖面仪［1-2］（以下简称 ADCP）出现。相较于传统的测流方式，ADCP测流实时性强、精度高、测速范围大，得到广泛应用［3-6］。随着水利事业的发展，定点水平式声学多普勒流速仪（H-ADCP）出现并引起广泛关注。例如，高怡［7］、杜耀东等［8］对ADCP的实际应用进行了分析，总结了ADCP在平原河网地区使用的优点和缺点，并提出了复杂条件影响下的H-ADCP改进方案。王萍等［9］提出了基于实时自动监测流量的引排水量计算精简分析方法，可为实时自动监测数据的精简分析提供借鉴。这些方法使得流量实时在线监测在部分断面得以实现，但在一些河道的特殊断面，如受自然潮汐和人为影响的大江大河的流量测验中，在线监测手段仍面临较大的挑战。

受汉江流域梯级开发的影响，汉江干流多个水文站测验断面水位流量关系改变较大。余家湖水文站是汉江干流基本控制站，之前水位流量关系主要受洪水涨落及断面冲淤的影响，呈多条临时曲线，关系较复杂。2022年10月，下游雅口航运枢纽蓄水后，该枢纽回水顶托影响严重，水位流量关系紊乱。传统的流量测验方法无法满足生产测验需求，因此汉江水文水资源勘测局提出了基于ADCP代表流速法“1+1”的多平台流量测验方法，结合水平式ADCP和垂直式ADCP，并通过代表流速法确定相关關系，以实现余家湖水文站流量在线监测。

本文以余家湖水文站为研究对象，探索基于ADCP代表流速法“1+1”的多平台流量监测在变动回水条件下的适用性，旨在实现汉江干流重要控制站的自动化流量测验，为巡测管理提供支撑。

1测站概况

余家湖水文站设立于1984年，测站位于湖北省襄阳市襄城区余家湖，地处长江流域汉江水系中游，控制流域面积130 624 km2。该站所处流域属亚热带季风区，气候温和湿润，多年平均降水量800 mm，水量较丰沛，主要来自丹江口水库下泄以及南北河和唐白河来水，年内分配不均，5～10月径流量占全年径流量62.6%左右，年际变化较大［10］。

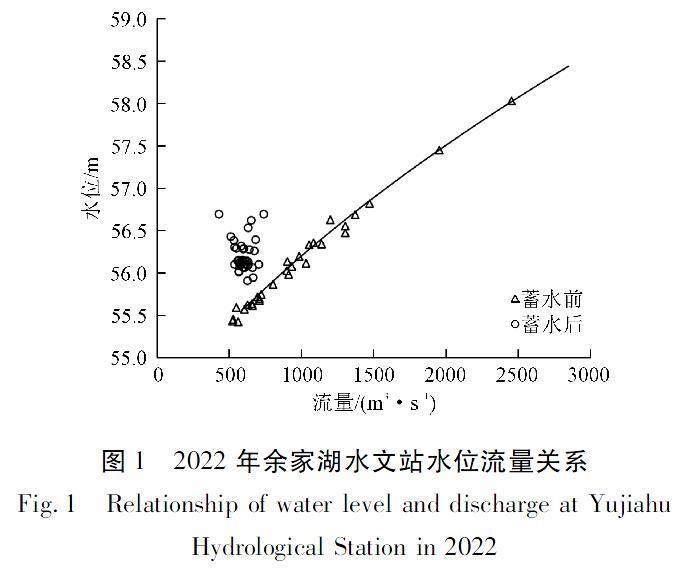
余家湖水文站所在河段较顺直，测验断面主槽宽约0.6 km。右岸为陡坎，左岸边滩宽2.4 km。断面为复式断面，呈“W”形，河床由砂卵石组成，断面最高水位65.03 m，最低水位55.49 m。该站断面水位主要受上游崔家营航电枢纽调机及开闸泄洪影响，水位流量关系主要受洪水涨落影响及断面冲淤影响［11］。河段调查最大流量52 400 m3/s，出现于1935年7月7日。丹江口水库蓄水运用后河段最大流量26 100 m3/s，出现于1983年10月7日。河段多年平均径流量391亿m3，多年平均悬移质输沙量620万t。2022年4月该站开始开展流量在线监测系统的比测工作。2022年10月下旬下游雅口航运枢纽开始试验性蓄水，受枢纽蓄水后变动回水的影响，该站水流特性发生显著变化。从图1的水位流量关系可以看出，在电站蓄水前该站水位流量关系单一，水位流量关系与往年一致；电站蓄水后受变动回水影响，水位流量关系点距分布散乱。

2比测方法

余家湖水文站于2022年初开展“1+1”多平台模式流量在线监测比测试验分析，其中，“1+1”为水平式ADCP（H-ADCP）和垂直式ADCP（V-ADCP），即通过收集走航式ADCP实测流量成果与同时段H-ADCP、V-ADCP的测验成果，建立实测断面平均流速与H-ADCP各单元区间代表流速以及V-ADCP垂线流速相关关系，以找出最优相关关系，确立H-ADCP代表流速Vh及V-ADCP垂线流速Vf与断面平均流速V的相关关系，以解决受回水顶托影响下的流量在线监测问题。

3数据收集及设备安装

3.1数据收集

本次研究主要收集了2022年4月下旬至2023年5月上旬走航式ADCP流量成果与同时段H-ADCP、V-ADCP的测验成果，并以走航式ADCP测流法的实测流量成果为实测值进行比测分析。走航式ADCP流量测验在崔家营电站正常发电调机期间按临时曲线法布设测次，其他时期按连时序法布置测次。任意一次测得流量与平均值的相对误差不大于5%，否则补测同向测次流量，直到满足相对误差不大于5%的要求；水位涨落急剧等特殊情况时只施测一个测回，但宜满足相对误差不大于2%的要求。同步比测期间，H-ADCP、V-ADCP的测验成果适当增加采样频次，以减少测验引起的随机误差。根据自动监测仪器及传输存贮设备性能，流量采样间隔与自记水位计采样时间保持一致（5 min）。

比测使用的走航式ADCP为WorkHorse 600 kHz河流型ADCP，其测量剖面深度范围为1.5～60.0 m，盲区0.25 m，最小单元深度0.5 m，最大单元数128个，流速测量分辨率0.1 cm/s，最大可测流速20 m/s，提供模式1、模式5、模式11共3种测量模式。该ADCP额定量程为60 m，实际量程与作业模式相关。

H-ADCP固定安装在水下某一深度，仪器水平方向发射信号，采集该深度水平层某一剖面范围内的水流速度即代表流速Vh。该站采用的H-ADCP为RDI公司的出品CM型600 kHz水平式ADCP，最大剖面范围为90 m，最小单元长度为0.5 m。利用Win H-ADCP（Ver 4.04）接口软件实现计算机与H-ADCP通信，并存贮数据。

该站采用的V-ADCP为RDI公司的出品RiverRay型走航式ADCP，系统频率为600 kHz，剖面量程为0.4～60.0m，最小单元长度为0.1 m，单元长度可根据水深自动调整。

3.2设备安装

H-ADCP安装在河段右岸，基本水尺断面下游14 m处。结合测站水流特征及断面情况，仪器的安装高程54.70 m。V-ADCP监测断面位于基本水尺断面下游30 m处。距H-ADCP监测断面下游约15 m。V-ADCP采用垂直支架式安装方式，将V-ADCP固定于某一入水深度，前期探头入水深约1.8 m，后根据断面水情情况调整至0.5 m。断面及设备安装示意见图2。

4计算方法

4.1代表流速法

代表流速法（Index-Velocity Method）最早由美国地质调查局（USGS）提出和应用［12-13］。代表流速法的基本原理是建立断面平均流速V与代表流速（即某一实测流速）之间的相关关系（即率定曲线或回归方程）。代表流速是河流或明渠过水断面上某处的局部流速［14］。率定代表流速与实测断面平均流速相关关系模型（即确定回归方程）时常用的回归方程型式见表1，其中一元线性回归方程及一元二次多项式回归方程较为常见，应用也较多；复合线性回归方程主要适用于复式河床、感潮河段等情况；加入水位H等变量的多元回归方程是当仅用代表流速作为模型输入无法获得较好精度时，改善模型精度的一种方法［15-16］。

4.2多要素数学拟合法

多要素数学拟合法即选取H-ADCP实测流速及其他的水力因素，以数学拟合方法与断面平均流速建立经验相关关系，这种关系称为断面推流关系［17］。相关关系的建立多采用多元线性回归方程。

多元线性回归是指研究一个因变量与两个或两个以上自变量的回归，是反映一种现象或事物的数量依多种现象或事物的数量的变动而相应变动的规律［18-19］。设Y为因变量，X1，X2，…，Xm為自变量，则多元线性回归方程模型可以采用公式（1）表达：

Y=β0+β1X1+β2X2+…+βmXm+ε（1）

式中：β0，β1，β2，…，βm为回归系数；ε为随机误差。

通常情况下，流量变化或断面流速变化与多种水力因素有关。水位H能够较直观地反映断面流量的变化［20］。余家湖水文站“1+1”多平台模式分别采集水平层区间代表流速Vh、固定起点距代表垂线平均流速Vf，结合H-ADCP入水深度H以反映该站水位变化情况，基于多元线性回归方程模型，采用以上3个自变量与实测断面平均流速建立多元函数关系，即断面平均流速V可认为是指标流速Vh和代表垂线平均流速Vf及H-ADCP入水深度H的函数：

V=f（H，Vh，Vf）

其表示为

V=C0+C1H+C2Vh+C3Vf（2）

式中：C0，C1，C2，C3为常数。

5比测结果分析

5.1代表流速单元区间优选

单元流速相关度的分布与测验仪器特性一致，在有效剖面范围内区间单元流速有一定的代表性，随着单元区间延伸，代表性降低。本研究在挑选代表流速单元区间时重点考虑1～40单元区间。根据下游电站蓄水情况，依照余家湖水文站测验河段水流特性选择变动回水期（2022年10月下旬至2023年5月上旬），共收集47个比测样本，实测流量变幅430～1 150 m3/s。通过挑选H-ADCP不同单元区间的平均流速作为代表流速与实测断面平均流速进行相关分析，利用correl函数分别计算不同单元区间的相关度，统计结果见表2。

从单元区间相关度的统计结果来看，相关度较优的代表流速区间集中在10～30单元，其中10～20单元流速有较优的相关度。因此在变动回水期比测分析时主要采用10～20单元作为代表流速单元区间。

5.2回归分析

依照计算方法所拟定的回归方程型式，对比分析各回归方程模型精度。采用多要素数学拟合法时，结合变动回水期水流特性，将下游参证站宜城水位站（位于余家湖水文站下游，距余家湖约35 km）落差引入多元回归线性回归模型。建立断面平均流速V与指标流速Vf、指标流速Vh、断面水位H以及余家湖水文站与宜城站落差ΔZ的函数关系：

V=f（H，Vf，Vh，ΔZ）

其表示为

V=C0+C1H+C2Vf+C3Vh+C4ΔZ（3）

式中：C0，C1，C2，C3，C4为常数。

将变动回水时期收集的比测样本按所拟定的回归方程型式进行回归分析计算。统计对应回归方程的相关系数，计算结果如表3所示，计算公式如下：

R=∑ni=1vi-vyi-y∑ni=1vi-v2∑ni=1yi-y2（4）

式中：R为相关系数，vi为实测值；yi为模拟值；v为所有实测值的平均值；y为所有模拟值的平均值；i为观测数据个数。

可以看出，将参证站落差ΔZ引入多元线性回归方程模型后，相关系数增大，能够有效地改善模型精度，因此选用多元线性4回归方程用作变动回水期回归分析，其代表流速相关关系见图3。

由图3可以看出，比测的相关关系点群较集中，测点无较明显的偏离，关系点距分布较均匀，取得的相关关系较理想。由此确定回归方程为

V=0.03388+0.1187Vh+0.2166Vf+0.0175ΔZ+0.0003H（5）

式中：Vh为H-ADCP代表流速，采用单元区间10～20单元格。

对变动回水期代表流速相关关系进行誤差统计，结果见表4。从误差计算结果来看，2022年Q58，Q78，Q79次误差较大，通过分析H-ADCP瞬时流速过程线、V-ADCP瞬时流速过程线、上下游落差过程线，可判断出导致偏离较大的原因：① 在线监测数据同步比测时有不同程度的数据缺失；② 从监测的瞬时过程线来看比测水情发生较大转折，样本代表性不好。因此，在进行误差统计时这些测点可不参与统计。除去以上3个测点，样本系列最大偏差10.9%，其余测点偏差均小于9%，占总样本97.7%。测点偏差小于8%占总样本93.2%。

根据确定的回归方程建立的断面平均流速与代表流速相关关系，依据SL 247-2020《水文资料整编规范》对率定的关系线需进行三项检验，即符号检验、适线检验和偏离数值检验，并对该关系曲线做定线精度指标分析，即分别统计比测的相关关系点距的系统误差及随机不确定度。计算公式如下：

P=1n∑pi（6）

Se=1n-2∑Qi-QciQci212（7）

X′Q=2Se（8）

式中：P为系统误差，%；pi 为相对误差，%；Se为实测点标准差，%；Qi为第i实测点流量，m3/s；Qci 为第i实测点的流量Qi在相应的曲线上的流量，m3/s；X′Q为置信水平为95.0%的随机不确定度。

进行符号检验时，分别统计测点偏离曲线的正、负号个数（偏离值为0时作为正、负各半点分配），按照公式（9）计算统计量u值，并将其与给定显著性水平α查表所得的u1-a/2值比较，当u＜u1-a/2时认为合理。

u=k-0.5n-0.50.5n（9）

式中：u为统计量；n为测点总数；k为正/负号个数。

进行适线检验时，按测点水位由低至高排列顺序，从第二点开始统计偏离正负符号变换，变换符号记1，否则记0。统计记“1”次数，按照公式（10）计算统计量u值，并将其与给定显著性水平α查表所得的u1-a/2值比较，当u＜u1-a/2时认为合理。

u=n-1p-k-0.5n-1pq=0.5n-1-k-0.50.5n-1（10）

式中：k为变换符号次数；p，q分别为变换、不变换符号的概率，各为0.5。

进行偏离数值检验时，按公式（11）、公式（12）分别计算t值、Sp值，并将t与给定显著性水平α查表所得的t1-a/2值比较，当|t|＜t1-a/2时则认为合理。

t=psp（11）

sp=sn=∑pi-p）2n（n-1）（12）

式中：t为统计量；p为平均相对偏离值；sp为p的标准差；s为p的标准差；pi为测点与关系曲线的相对偏离值。

精度指标和三项检验的检验结果见表5，检验结果符合SL/T 247-2020《水文资料整编规范》要求（中系统误差不大于±2%，随机不确定度不大于10%）。

6结论与建议

6.1结论

本文基于ADCP代表流速法“1+1”的多平台流量测验，结合代表流速法以及多要素数学拟合法，在余家湖水文站进行了比测分析，从比测实验结果来看，仪器性能稳定，流量测验能够取得较好的测验精度，采用“1+1”多平台流量测验方法可行，并得到以下结论。

（1） 分别统计比测的相关关系点距的系统误差及随机不确定度，并对率定的关系线进行三项检验，检验结果均符合规范要求，说明断面平均流速与代表流速相关关系较好，即可通过水平式区间代表流速Vh及V-ADCP垂线流速Vf关系式拟合代替断面平均流速V。

（2） 余家湖水文站因水利工程影响，测验河段常年处于变动回水区，从比测的分析结果来看，将H-ADCP和V-ADCP结合的流量在线监测的方法能够解决该站因变动回水影响下流量监测问题。

6.2建议

（1） 通过比较不同回归方程定线精度，最终优选基于多元线性回归方程的回归模型，由于回归模型引入多个变量，有助于提高回归模型精度，同时也引入了更多的误差来源，因此在相关关系率定时需排除多个变量中误差的影响，同时在比测时要充分考虑比测样本代表性问题。

（2） 通过比较不同回归方程定线精度，基于多元线性回归方程的回归模型作为第一优选方案，其他回归方程定线精度在满足规范规定的误差要求时，可作为备用方案。

参考文献：

［1］闫慧敏.基于机器视觉的复杂背景下的河流水位检测［D］.西安：西安电子科技大学，2021.

［2］杨永寿.环境适应性声学多普勒测流方法研究［D］.南京：东南大学，2021.

［3］王秀波.宽带多普勒测流技术研究［D］.哈尔滨：哈尔滨工程大学，2005.

［4］宋乾坤.多频多信号ADCP流速测量技术及实现方法研究［D］.南京：东南大学，2021.

［5］刘彦祥.ADCP 技术发展及其应用综述［J］.海洋测绘，2016，36（2）：45-49.

［6］馬雅丽，彭昆.汉江流域梯级水库群优化调度研究［J］.水利规划与设计，2020（2）：63-66，101.

［7］高怡.ADCP在太湖流域平原河网地区的应用［J］.水利水文自动化，2005（3）：30-31.

［8］杜耀东，宋星原，王俊.H-ADCP在复杂环境下的应用［J］.人民长江，2008（3）：57-59.

［9］王萍，谢运山，姚允龙.基于实时自动监测流量的引排水量计算精简分析［J］.人民长江，2022，53（8）：94-99.

［10］段唯鑫.汉江流域控制性水库调度运行及影响研究［D］.武汉：武汉大学，2017.

［11］谢雅蕾，柯莉莉，谢波.长江下游干流八里江水文站水位流量关系分析［J］.水利水电快报，2023，44（3）：26-29.

［12］RANTZ S E.Measurement and computation of streamflow［M］.Liston：U.S.Geological Survey，1982.

［13］MORLOCK S E，NGUYEN H T，ROSS J H.Feasibility of acoustic Doppler velocity meters for the production of discharge records from US Geological Survey streamflow-gaging stations［M］.Liston：U.S.Geological Survey，2002.

［14］杨永怀.基于超高频雷达的河流流量反演算法研究［D］.武汉：武汉大学，2020.

［15］蒋春丽.LUCC对平均气温变化的敏感性分析——以东北北部为例［D］.哈尔滨：哈尔滨师范大学.

［16］孙前，陈方，刘金涛，等.基于影响因子数据年际分类的太湖典型口门流量估算方法［J］.河海大学学报（自然科学版），2017，45（3）：218-223.

［17］王凯燕，季海萍，李鹏程，等.饮用水水源地上游重点断面流量预报研究——以平原河网感潮河段为例［J］.人民长江，2021，52（增1）：68-72.

［18］周绍阳，谢雅蕾，蒋建平.基于代表性垂线流速的在线流量测验方法研究［J］.水利水电快报，2023，44（4）：28-33.

［19］吴志勇，徐梁，唐运忆，等.水文站流量在线监测方法研究进展［J］.水资源保护，2020，36（4）：1-7.

［20］刘墨阳，蒋四维，林云发，等.复杂水情下H-ADCP流量在线监测推流方法［J］.水利水电科技进展，2022，42（2）：27-34.

（编辑：江文）

Research on multi-platform flow test comparison based on ADCP representative flow method "1+1"

ZHANG Danfeng，WANG Wenjuan，YOU Jiawei，WU Yunhao，RAO Yong

（Hanjiang Bureau of Hydrology and Water Resources Survey，Bureau of Hydrology of Changjiang Water Resources Commission，Xiangyang 441000，China）

Abstract： In order to improve the accuracy of flow measurement in backwater area，and provide a strong support for patrol management，a multi-platform flow measurement method based on ADCP representative flow rate method "1+1" was proposed.The correlation between the measured average flow rate in section，the horizontal ADCP representative flow rate and the V-ADCP vertical flow rate were established.The optimal regression equation was determined by comparing the accuracy of different regression equation types.At the same time，the alignment accuracy of the correlation relationship established by the regression equation was tested according to the requirements of the specification.The results showed that the alignment accuracy of the three tests was 0.45，0.61 and 0.34，respectively.The alignment accuracy of the correlation relationship was in line with the requirements of the relevant specifications，indicating that the ADCP representative velocity method was suitable for Yujiahu Hydrological Station and had a good value for promotion.

Key words： flow measurement； ADCP； representative flow method； regression analysis； Yujiahu Hydrological Sta-tion