电子温度各向异性对螺旋波m=1 角向模功率沉积特性的影响*

李文秋 唐彦娜 刘雅琳 王刚2)

1) (中国科学院空天信息创新研究院,北京 100190)

2) (中国科学院大学,北京 100049)

采用一般的径向密度非均匀分布假设,借助温等离子体介电张量模型,利用磁化等离子体中电磁波的一般色散关系,在高密度峰值、低磁场、低气压典型参量条件下,重点分析了电子温度各向异性对螺旋波 m=1 角向模功率沉积特性的影响.研究结果表明: 在典型螺旋波等离子体电子温度范围(3,8) eV 内,电子有限拉莫尔半径效应应当予以考虑,而离子有限拉莫尔半径效应可以忽略.低磁场条件下 |n|＞1 次回旋谐波对介电张量元素的贡献可以忽略.碰撞阻尼在功率沉积中占据主导地位,功率沉积在偏离等离子体柱中心轴的某一径向位置出现峰值,随着轴向电子温度Te,z 的增大,功率沉积强度逐渐增强.相比等离子体温度各向同性情形,等离子体温度各向异性显著改变了螺旋波m=1 角向模的功率沉积特性,电子温度各向异性因子 χ=Te,⊥/Te,z 的增大或减小均导致功率沉积强度发生剧烈改变.

1 引言

在螺旋波等离子体放电过程中,更为一般的情形是形成的等离子体在径向具有陡峭的密度梯度,这种密度梯度不仅可以通过 ∇P×B作用显著改变等离子体的输运特性[1-3],更重要的是,它从根本上改变了等离子体中电磁模式的传播条件和特性[4-6],从而给我们理解螺旋波等离子体放电过程带来了更大的难度.2000 年,在低轴向波数条件下,Breizman 和Arefiev[7]在理论上首次发现了非角向对称模由径向密度梯度引起的径向势阱,结果表明在异常低频的螺旋波放电中存在射频功率有效共振吸收的可能性.2006 年,Chen 等[8]在实验中观测到以接近射频天线驱动频率传播的螺旋波在轴向呈驻波结构,此螺旋波以共振吸收的形式在整个射频波功率沉积过程中占据主导地位.与此同时,Arefiev 和Breizman[9]进一步发现沿轴向静磁场急剧下降的轴向密度分布可以导致螺旋波几乎被完全反射,且在这一过程中一小部分波的能量通过模式耦合转换机制转变为Whistler 波.2008年,在考虑径向电子密度梯度的条件下,Aliev 和Krämer[10]研究发现在大密度梯度情形下,静电模和电磁模的模式转换条件会发生改变,如果密度梯度足够陡峭,可以在更低的密度值处发生模式转换.2014 年,他们发现当存在模式耦合时,电磁波场型会发生剧烈的变形,从而导致在等离子体柱中心轴处的功率沉积愈发强烈[11].2016 年,借助简单的天线-等离子体模型,他们发现模式传播的密度限制和窄磁场分布特点是m=-1 角向模无法主导功率沉积的原因[12].2023 年,更进一步的分析结果表明大密度梯度引起的模式共振机制可用于电子加热[13].在国内,成玉国等[14]数值分析了径向电子密度呈抛物线型分布情况下径向电、磁场强度及能量沉积特性;赵高等[15]通过实验研究了螺旋波等离子体的放电特性,获得了射频功率吸收因放电模式转变而变化的方式.

等离子体温度各向异性特性作为螺旋波等离子体中的重要现象[16,17],因其涉及到复杂的动理学效应,因此一直是螺旋波等离子体放电理论与实验研究中的难点.为探究等离子体温度各向异性对螺旋波等离子体中电磁波模式功率沉积特性的影响,本文在考虑等离子体有限拉莫尔半径效应和温等离子体介电张量模型情形下(同时也是更加符合螺旋波等离子体放电的实际情形),理论分析了等离子体温度各向异性在螺旋波m=1 角向模功率沉积中扮演的作用,作为解决这个难题的初步尝试,本文采用更为一般的径向密度非均匀分布假设,在螺旋波等离子体典型参量条件下,分析了电子温度各向异性对螺旋波m=1 角向模功率沉积特性的影响,所得结果为进一步理解螺旋波等离子体放电机制提供了理论线索.

2 理论模型

图1 为螺旋波放电产生等离子体的横向截面示意图.半径为a的等离子体柱被玻璃管包裹,浸没在轴向静磁场B0ez中;玻璃管放置在半径为b的真空腔体中;位于玻璃管外壁附近的是螺旋波天线,其携带的射频功率电流放电产生径向密度非均匀分布的等离子体轮廓;假定等离子体中离子携带单位正电荷,且其温度远小于电子温度.

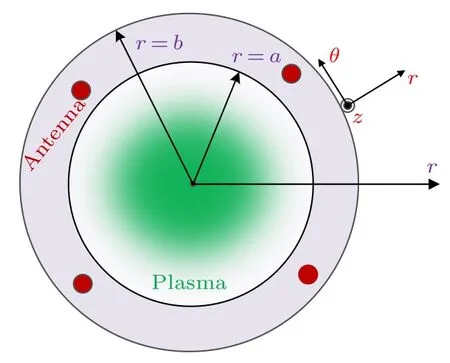
图1 螺旋波放电产生等离子体柱横向截面示意图Fig.1.Cross section of helicon wave discharge plasma column.

在图1 所示的圆柱坐标系(r,θ,z) 下,假定扰动电磁场具有形式,根据Maxwell方程组:

得到关于电磁场横向分量的波动方程:

其中,m为角向模数,kz为轴向波数,ω为波频率;横向拉普拉斯算表示为

式中,符号⊥表示垂直于轴向静磁场的横向方向;k⊥,TG和k⊥,H分别表示短波Trivelpiece-Gould 波(TG 波)和长波螺旋波的横向波数;ϵ为等离子体介电张量,在麦克斯韦速度分布等离子体中,假定等离子体温度各向异性,温等离子体介电张量元素为[18]

(8)式右侧第一项代表电子与绝缘壁之间的碰撞,第二项为电子-离子碰撞效应,第三项代表电子与中性工质气体碰撞电离;其中 lnΛ=23-为电子-离子库仑对数;A为工质气体原子质量数;nn=3.54×1013pArcm-3为中性工质气体密度[21],pAr为工质气体(氩气)气压,单位为mTorr (1 Torr=133.32 Pa);σen=5×10-15cm2为电子-氩气碰撞截面; In(·) 为n阶第一类修正贝塞尔函数;等离子体色散函数Z(ζ) 定义为[22]

利用全波分析方法,求解(3)式,得到以下描述电磁波纵向分量的耦合方程组[10]:

其中,Nz=kz/k0为折射率;k0=ω/c为真空波数;c为光速;f和g分别为

在螺旋波等离子体中,TG 波和螺旋波的横向波数可以通过求解下式色散方程得到:

特别地,在均匀等离子体中,上式色散关系变为[23]

式中,R=ϵ⊥+ϵ∠;L=ϵ⊥-ϵ∠.当TG 波和螺旋波的横向波数相等时,即可发生模式耦合,此时等离子体参量满足下列关系式:

其中,

注意到(17)式是关于求解模式耦合层(mode coupling surface,MCS)位置(r0)的隐式方程.

在典型螺旋波等离子体频率条件ωci≪ω≪ωce≪ωpe下,数值求解(15)式,得到TG 波和螺旋波的横向波数;然后求解(11)式和(12)式,分别得到TG 波和螺旋波的场型分布;最后利用(20)式求得电磁波的功率沉积[24]:

其中,J为等离子体电流;Er,Eθ及Ez分别为等离子体中径向、角向及轴向电场分量.

本文主要研究螺旋波m=1 角向模的功率沉积特性,在分析过程中,采用寻根函数fsolve 求解色散(15)式;计算中假定工质气体为氩气 (A=40),其波频率ω=13.56 MHz,轴向静磁场B0=48 G(1 G=10-4T),中性气体气压pAr=0.5 mTorr,等离子体柱半径a=3 cm,等离子体密度峰值n0=1×1013cm-3,离子轴向温度与电子轴向温度之比Ti,z/Te,z=0.1.

3 数值计算与结果分析

在分析模式耦合特性之前,需要对螺旋波等离子体中存在的波阻尼机制予以分析,典型的阻尼机制包含碰撞阻尼(collisional damping,CD)和朗道阻尼(Landau damping,LD).由于离子热速度远远小于电子热速度,在计算阻尼频率过程中仅考虑电子项阻尼机制.为直接、简洁地对各项阻尼机制的相对重要性做出量化比较,在等离子体温度各项同性 (Tℓ,⊥/Tℓ,z=1)条件下,采用理论分析公式νLD=(νLD表示朗道阻尼引起的阻尼频率,ζe=ω/kzvthe)[25],图2 给出了碰撞阻尼频率和朗道阻尼频率随电子温度的变化特性,在当前高密度、低磁场条件下,碰撞阻尼和朗道阻尼在不同电子温度范围内占据统治地位.在典型螺旋波等离子体电子温度范围Te∈(3,8)eV 内[24],随着电子温度的增大,碰撞阻尼频率逐渐减小而朗道阻尼频率逐渐增大;当Te＞5.4 eV 时,朗道阻尼超过碰撞阻尼在整个电磁波能量沉积占比中占据主导地位.这是因为随着电子温度的增大,电子热速度逐渐接近电磁波的相速度,朗道阻尼效应逐渐增强;而碰撞阻尼中电子-离子间碰撞效应引起的碰撞阻尼随着电子温度的增大而显著减小,尽管电子与中性工质气体之间的碰撞阻尼因电子温度的增大会增加,但增加的幅值不足以抵消电子-离子间碰撞阻尼的减小量,故总碰撞阻尼呈现减小趋势.

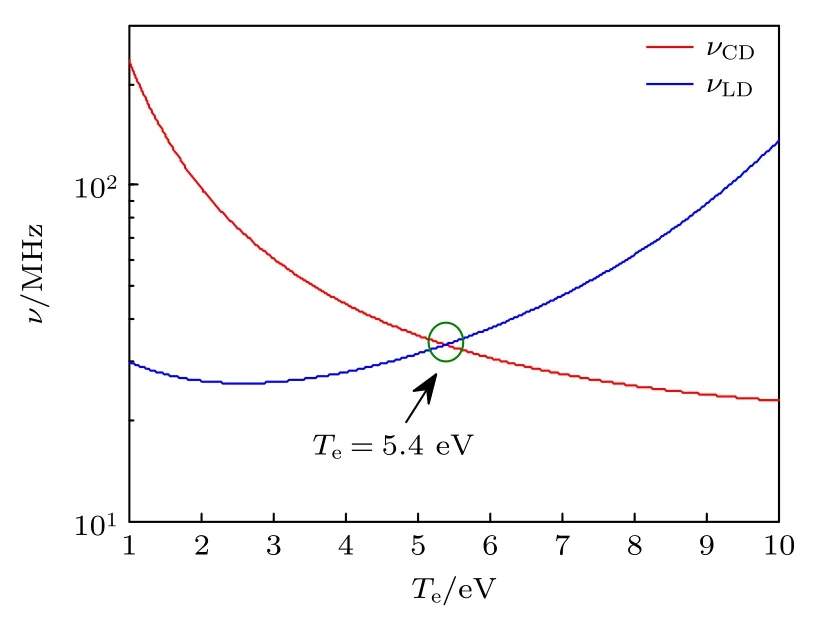
图2 碰撞阻尼频率与朗道阻尼频率随电子温度的变化Fig.2.Dependence of the collisional frequency and Landau frequency on the electron temperature.

作为影响分析过程的一个核心参量,等离子体介电张量元素中的有限拉莫尔半径效应因子λℓ从根本上决定了计算结果的精度,从其定义可以看到,其大小取决横向波数、电子/离子横向温度及静磁场强度三个参量,轴向静磁场参量作为影响λℓ的最重要因素,在进行后续的计算之前需要先分析其对λℓ的影响.定义χ=Te,⊥/Te,z为电子温度各项异性因子,在χ=0.1,Te,z=3 eV 及kz=1 cm-1参量条件下,基于(16)式,图3 给出了在B0∈(10,1000)G 范围内λℓ随轴向静磁场的变化特性,可以看到,因子λi和λe具有不同的幅值强度,λe～10-4λi,这是因为离子质量远远大于电子质量,惯性效应导致离子回旋半径远大于电子回旋半径,表现为电子被冻结在磁力线上,而相比电子离子几乎不受磁力线的约束;随着磁场的逐渐增大,λi和λe的幅值均逐渐减小(注意到在B0≈22 G 和B0≈170 G 处λℓ出现极值,这可能是由于在这些位置发生电磁波模式耦合转换和能量共振耗散,导致电子/离子绕磁力线的回旋动理学过程出现扰动),这是因为随着磁场强度的增大,磁力线对电子/离子的冻结效应逐渐增强,表现为电子/离子的回旋半径逐渐减小,进而导致λℓ的幅值减小;对于本文分析中的低磁场情形,B0=48 G,图3 表明此时λi≈517,λe≈0.07.这一结果暗示,此时在计算等离子体介电张量元素时离子项可以忽略,这是因为项使得离子计算项趋于零.

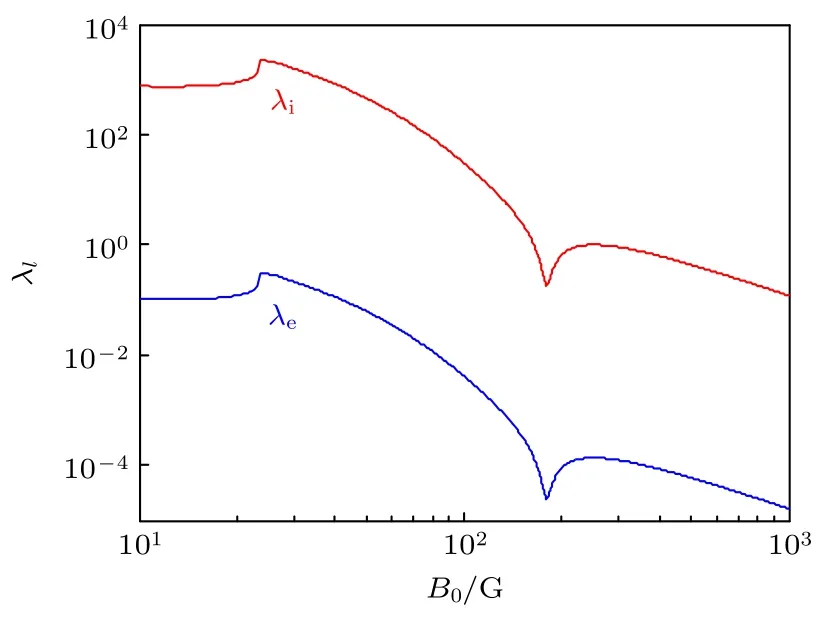
图3 有限拉莫尔半径效应因子随轴向静磁场的变化Fig.3.Dependence of the FLR effects on the axial static magnetic field.

另一个决定计算结果精度的参量是等离子体色散函数宗量中的回旋谐波次数,在χ=0.1 及k⊥=1 cm-1参量条件下,基于(16)式,图4 给出了在Te,z∈(1,10)eV 范围内 |ζn,e| 随轴向电子温度的变化特性.结果表明,在所有的回旋谐波次数中,n=0次谐波对应的宗量具有最小幅值,其次是|n|=1 次谐波;随着|n|的增大,对应的宗量的幅值逐渐增大;对于典型螺旋波等离子体电子温度Te,z=3 eV,图4 表明此时 |ζ0,e|=0.62,|ζ-1,e|=5.15,|ζ1,e|=6.3,|ζ-2,e|=10.88 ,|ζ2,e|=12.05 .这些结果表明,在等离子体介电张量元素计算过程中,|n|≥2 次谐波可以忽略,只保留 |n|≤1 次谐波即可.

图4 |n|≤3 次回旋谐波对应的色散函数宗量随电子温度的变化Fig.4.Dependence of the argument of the plasma dispersion function on electron temperature for the |n|≤ 3 cyclotron harmonics.

采用高斯型密度轮廓分布Γ(r)=,参量γ用来控制密度梯度,此时电子-壁碰撞阻尼频率是半径的函数.图5 给出了γ=0.01 m 情形下等离子体密度np及电子-壁碰撞频率νe-wall的径向分布,对于非均匀密度分布,电子-壁碰撞频率νe-wall在某一径向位置取得最大值.图5 中的子图显示在当前参量条件下,此最大值对应的径向位置约在r=1.48rLe处,这表明通过电子-壁碰撞阻尼机制沉积的电磁波能量在径向具有非均匀特性,这为深入理解电磁波能量沉积过程提供了思路.

图5 高斯型等离子体密度及电子-绝缘壁碰撞频率的径向分布Fig.5.Radial profile of the plasma density distribution and electron-wall collisional frequency.

电磁波在等离子体柱中传播时,其部分能量沉积入等离子体中,通常用传播常数表征电磁波的衰减特性,在有损介质中,传播常数具有复数形式,即kz=β+jα,其中β为相位常数(单位: rad/m),α为衰减常数(单位: Np/m).在Te,z=3 eV,χ=0.1及k⊥=1 cm-1参量条件下,图6 为相位常数和衰减常数的径向分布特性,计算结果显示,在图5 所示的密度轮廓 (γ=0.01 m)条件下,在归一化半径 (r/rLe) 范围内,随着r/rLe的增大(即等离子体密度的减小),相位常数先逐渐增大,在r≈1.45rLe处取得最大值,而后随着r/rLe的继续增大而持续单调减小,直至在等离子体柱边缘处取得最小值;对于衰减常数,其幅值变化轮廓与等离子体密度轮廓吻合,其在等离子体柱中心位置取得最大值,在等离子体柱边缘处取得最小值.值得注意的是,相位常数与电子-壁碰撞频率在非常接近的径向位置取得峰值,这暗示电磁波的传播与其能量沉积存在密切的关联.这些结论表明,电磁波在等离子体中的传播受到等离子体密度的调控,其能量沉积也与密度幅值关系密切.

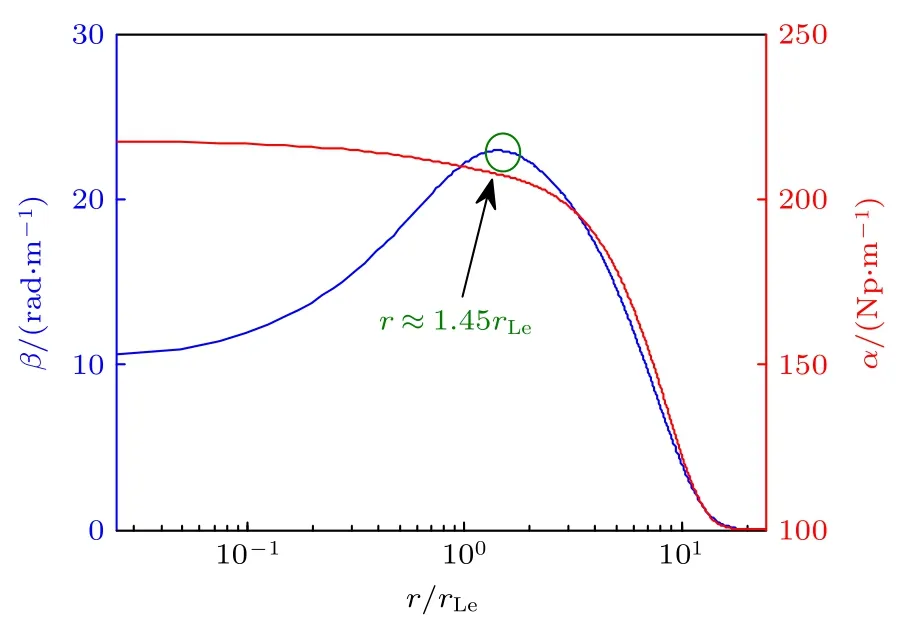
图6 相位常数和衰减常数随归一化半径的变化特性Fig.6.Amplitude of phase and attenuation constants varies with normalized radial position.

在径向密度非均匀分布螺旋波等离子体中,存在由密度梯度引起的电磁模式耦合转换现象.计算电磁波能量沉积之前,有必要首先对不同电磁波模式的横向波数分布特性和它们之间的耦合转换特性予以分析.接着上面的分析,在γ=0.01 m,Te,z=3 eV,χ=0.1 及kz=1 cm-1参量条件下,采用归一化半径变量r/rLe.图7 中的计算结果显示: 在当前参量条件下,等离子体中同时存在TG 波和螺旋波;随着径向等离子体密度的变化,TG 波和螺旋波对应的横向波数随之发生显著改变.图7 中的子图显示TG 波和螺旋波在r≈5.875rLe处发生模式耦合;在等离子体柱边缘附近区域(约a/6 厚度区域内),螺旋波波数为零,这暗示在这一区域螺旋波无法传播,因为其传播存在最低密度阈值要求;而对于TG 波,图7 显示在当前参量条件下其可以在整个径向区域内传播.以上结论表明,在径向密度非均匀分布和低磁场条件下,在进行电磁波能量沉积计算之前,必须首先明确等离子体中存在何种电磁波,以及其对应的传播区域,这种预先分析可以为我们之后进行的电磁波能量沉积定量分析提供参量指引.

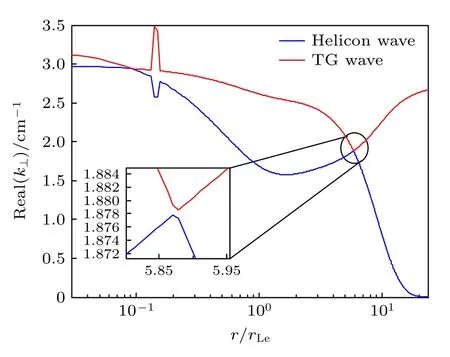
图7 螺旋波和TG 波的径向模式耦合特性Fig.7.Mode coupling characteristic of helicon and TG waves on the normalized radial position.

在以上分析的基础上,采用抛物线密度分布,在χ=0.1 及kz=1 cm-1参量条件下,图8 给出了由朗道阻尼和碰撞阻尼共同引起的功率沉积Pabs在 (r,Te,z) 空间的归一化分布.由图8(a)可知,当电子温度各项异性因子给定时 (χ=0.1),在典型螺旋波等离子体电子温度范围Te,z∈(3,8)eV 内,功率沉积Pabs随着轴向电子温度Te,z的增大而逐渐增强,在径向功率沉积则呈现抛物线分布特性,在某一径向位置取得峰值(当前参量条件下在r≈1.2 cm处);此外,当增大等离子体密度时,图8(b)计算结果表明密度的变化并未改变功率沉积的轮廓特征.更进一步,为详细探究朗道阻尼和碰撞阻尼在螺旋波m=1 角向模功率沉积中扮演的角色,在与图8 分析结果相同参量条件下,图9给出了由朗道阻尼引起的功率沉积Pabs,LD和由碰撞阻尼引起的功率沉积Pabs,CD在 (r,Te,z) 参量空间的分布特性.计算结果表明,随着轴向电子温度的增大,Pabs,LD和Pabs,CD的幅值均逐渐增大;在径向,Pabs,LD和Pabs,CD均呈现抛物线分布特性,且均在某一径向处取得峰值;相较朗道阻尼,碰撞阻尼在螺旋波m=1 角向模功率沉积中占据主导地位.这是因为随着轴向电子温度的增大,电子与中性原子之间的碰撞效应增强,使得更多的电磁波能量用来电离中性原子,导致由碰撞阻尼引起的功率沉积逐渐增大;同时,随着轴向电子温度的增大,电子的轴向速度逐渐靠近波相速,使得朗道阻尼效应愈发显著,导致由朗道阻尼引起的功率沉积也逐渐增大.另外,螺旋波m=1 角向模的功率沉积主要集中在偏离等离子体柱中心轴处,这可能与波的传播特性有关,图6 显示相位常数β亦在偏离等离子体柱中心轴处取得峰值.

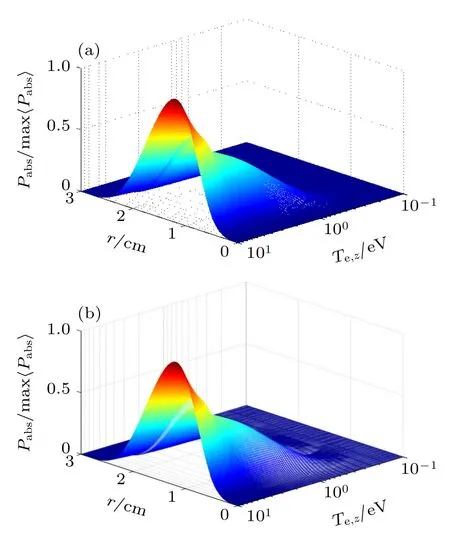
图8 归一化功率沉积Pabs/max＜Pabs＞在(r,Te,z)参量空间的分布 (a) n0=1×1013 cm-3;(b) n0=1.2×1013 cm-3Fig.8.Distribution of normalized power deposition Pabs/max＜Pabs＞ in the (r,Te,z) parameter space: (a) n0=1×1013 cm-3;(b) n0=1.2×1013 cm-3.

图9 朗道阻尼(a)和碰撞阻尼(b)引起的功率沉积在(r,Te, z)参量空间的分布Fig.9.Landau damping (a) and collisional damping (b) induced power deposition in the (r,Te, z) parameter space.

为更详细地分析螺旋波m=1 角向模的能量沉积特性,接着上面的分析,在Te,z=3 eV 及kz=1 cm-1参量条件下,图10 给出了由碰撞阻尼导致的功率沉积在r∈(0 cm,3 cm) 和χ∈(0.1,10)变量空间的分布特性.分析结果显示,与图8 分析结果相同,由碰撞阻尼导致的功率沉积Pabs,CD在偏离等离子体柱中心轴的某一径向处取得峰值;电子温度各项异性对功率沉积特性具有根本性的影响,当χ＜1 时,即横向电子温度小于轴向电子温度,功率沉积随着χ的减小逐渐增强,并在χ=0.1处存在极大值;当χ＞1 时,随着χ的增大,功率沉积幅值并非单调变化,其在χ=10 处存在最大值.此外,图10(a)—(c)表明,在低磁场条件下,磁场强度的变化并未改变功率沉积在m=1 值范围两端 (m=1 处和m=1 处)分别取得极大值和最大值的特性.电子温度各项异性对功率沉积特性的根本性影响不仅体现在螺旋波m=1 角向模功率沉积聚焦的位置发生了改变,同时也显著地影响了功率沉积强度.这些改变背后的原因是复杂的,既涉及到电磁波与等离子体之间的动理学相互作用,同时也与电磁波在轴向和横向上不同的能量沉积机制有关,轴向电子温度和横向电子温度的大小及两者的比值,直接决定了电磁波在轴向和横向受到的阻尼大小.综合以上分析,可以看到电子温度各项异性对我们深入理解螺旋波等离子体的放电过程至关重要.

图10 (二维)条件下归一化功率沉积Pabs,CD/max＜Pabs,CD＞在 (r,χ) 参量空间的分布 (a) B0=32 G;(b) B0=40 G ;(c) B0=48 G;(d)B0=48 GFig.10.Distribution of normalized power deposition Pabs,CD/max＜Pabs,CD＞ in the (r,χ) parameter space (two dimensional):(a) B0=32 G;(b) B0=40 G;(c) B0=48 G;(d) B0=48 G.

4 结论

在径向密度非均匀分布螺旋波等离子体中,考虑等离子体温度各向异性特性及动理学效应,理论分析了高密度、低磁场、低气压条件下等离子体柱中螺旋波与TG 波的模式耦合特性,并定性分析了螺旋波m=1 角向模的功率沉积特性,研究结果表明: 1)在低磁场情形下,电子及离子的回旋效应各不相同,电子趋于被“冻结”在磁力线上,导致其有限拉莫尔半径效应需以考虑;而离子由于其质量惯性作用,可忽略其有限拉莫尔半径效应.2)在等离子体温度各向同性情形下,碰撞阻尼和朗道阻尼在不同的电子温度范围内占据主导地位,且存在一个临界电子温度,超过此临界温度,朗道阻尼起到主导作用.3)在等离子体温度各向异性情形下,回旋谐波次数决定了等离子体色散函数宗量的幅值,|n|≥2 次谐波对宗量的贡献可以忽略;m=1 角向模的相位常数(传播常数的实部)在r≈1.45rLe处存在最大值,同时螺旋波与TG 波在r≈rLe处存在模式耦合.4)等离子体温度各向异性从根本上改变了螺旋波m=1 角向模的功率沉积特性: 对于给定的等离子体温度各向异性因子χ,在典型螺旋波等离子体电子温度范围Te,z∈(3,8)eV 内,随着轴向电子温度的增大,功率沉积逐渐增强且在偏离等离子体柱中心轴处取得峰值,碰撞阻尼相较朗道阻尼在功率沉积中占据主导作用;在χ∈(0.1,10)范围内,碰撞阻尼导致的功率沉积分别在χ=0.1和χ=10 处取得极大值和最大值.不同于前人采用冷等离子体介电张量模型和密度均匀分布假设,本文在考虑等离子体有限拉莫尔半径效应和温等离子体介电张量模型情形下,得到了这些更加符合螺旋波等离子体放电实际情形的结论,发现了电子温度各项异性对由碰撞阻尼和朗道阻尼导致的功率沉积具有非常显著影响这一最重要的结论.这一发现为揭示螺旋波等离子体电离特性背后的物理机制提供了重要的理论线索.