运动目标的多维度微运动特征提取研究*

陈思 张海洋 靳发宏 汪林 赵长明

(北京理工大学光电学院,北京 100081)

微多普勒特征提取作为一种常用的时频分析工具,对微动目标特征的提取重构具有重要意义.为了更好地研究多运动的微多普勒效应,提出了一种运动姿态分类方法.按照目标频移是否随时间变化可以将运动姿态分为频移时变运动和频移时不变运动.频移时变运动包括平移、翻滚和振动.针对这种运动应分析对比不同时间对应的瞬态频移,频移时不变运动主要为旋转运动.本文通过微多普勒效应理论结合电磁波频域模型,实现3D 运动目标微动特性提取的仿真建立目标,分析不同环境条件例如晴天阴天、有无湍流对探测的影响,为后续实验研究奠定理论基础.开展基于收发同置系统的多特征运动目标的微多普勒频移探测实验,实验结果表明,不同目标位置上频移的幅度、正负性和谱线宽度旨在反演目标形状、运动姿态、运动方向和速度.利用FFTshift 函数对一维数据进行解调分析,实现三维时间-频率-强度关系的研究.本研究实现了对目标宏观形状特性的测量以及微观运动信息的提取,为雷达探测和识别奠定基础.

1 引言

微多普勒效应[1,2]是由物体及其组件的微运动产生的一种物理现象.微多普勒特征的提取对于提高雷达的探测和分辨率[3]、目标识别[4]以及雷达成像[5]性能的提升具有重要意义.通常使用传统的傅里叶变换处理时域信号[6]再通过频谱与中心频率的偏差来观察微多普勒频移[7],随着技术的发展,研究者们在傅里叶变换的基础上对算法进行改进.文献[8]利用检测和分类算法设计了一种用于微多普勒研究的多频连续波雷达,收集了不同的调频连续波雷达微多普勒特征数据库,包括来自人类、车辆和动物目标的实验数据,以实现章动锥的节点和底部散射源的理论微多普勒效应[9].利用贝塞尔函数[10]实现了高阶谐波分量的分解.文献[11]提出了一种高度局部化的数据关联方法,即本征同步压缩分析.该方法能够实现通过双通道雷达从小型无人机的返回信号中估计微多普勒特征.

总体来说,上述研究常见于自旋、振动等目标的整体微动特性研究,鲜少针对振动、翻滚等目标的微多普勒效应实验研究.究其原因,振动、翻滚等运动的频率-强度关系在一定程度上是时变的.另外,这些方法难以直观地提供例如目标姿态分类、运动方向、运动速度等的时变频率调制信息.为了实现对运动目标微动信息的解调以期精准探测定位[12],本文提出了一种运动姿态分类方法.即当运动目标被照射面元的整体大小不随时间变化时,对应的频移也不具有时变性,定义这种运动为“频移时不变运动”;反之,则称为“频移时变运动”.基于该分类方法,以自旋和振动目标为例,在微多普勒效应解析法和电磁波频域模型的基础上利用有限元分析完成三维目标时频关系的仿真.此外,开展相对湿度、能见度以及有无湍流等环境条件对实验所得回波强度以及时频关系影响仿真实验研究.利用收发同置系统[13]展开对不同运动目标微动特性的研究实验.对于自旋这种频移时不变运动,可以直接获取目标上不同位置的一维微多普勒频移曲线;针对平移、翻滚、振动这3 类频移时变运动,则有必要对比不同时间的瞬时频移.振动和翻滚是随时间周期性变化的频移时变运动,需要一个周期内任意3 个时刻的瞬时频移进行对比.而平移是一种随时间不规则变化的频移时变运动,即任取3 个时刻的瞬时频移开展研究.实验结果表明,目标形状、运动类型、速度和方向可以通过频移的大小、正负、包络形状和谱线宽度来反演.对实验数据进行三维时频强度分析并讨论误差产生原因,这种多维参数处理的方法在雷达、声纳、通信的领域应用广泛,实现运动目标宏观信息的测量和微观特征的提取,为目标精准定位的实现奠定基础.

2 运动目标的频移仿真研究

2.1 理论模型

假设目标是一个刚体,其相对于雷达的平移速度为V,旋转角速度为ω=(ωx,ωy,ωz)T,其可以在目标局部坐标系中表示为=(ωx,ωy,ωz)T[14,15].通常来说,时间和频率之间的关系是基于将目标视作散点,研究其运动的几何特征建立的.一般来说,雷达位于雷达坐标系(U,V,W)的原点处,点散射体P围绕中心点O振动.中心点也是参考坐标系(X,Y,Z)的原点,该坐标系从距离雷达R0处的(U,V,W)平移而来.雷达是静止的,位于雷达坐标系(U,V,W)的原点Q处.目标在附着于其上的局部坐标系(x,y,z)中进行描述,并具有相对于雷达坐标的平移和旋转.为了观察目标的旋转,引入了参考坐标系(X,Y,Z),假设参考坐标的原点O位于距离雷达的距离R0处.t时刻,散点位于P′,则从Q处的雷达到该处粒子的距离矢量可以推导为QP=R0+Vt+ℜtr0,标量范围变为

其中ℜt为旋转矩阵,‖·‖为欧几里得范数,R0表示探测距离,Vt表示带有平移速度的位移项,ℜtr0表示带有自旋速度的位移项.(1)式能够表征不同运动状态或运动状态组合条件下对应的位移.根据(1)式可将返回信号写作:

其中,ρ(x,y,z)是在目标局部坐标(x,y,z)中描述的点散射体P的反射率函数,c是光速,通过取相位的时间导数,可以获得目标运动引起的多普勒频移:

其中,n=(R0+Vt+ℜtr0)/(‖R0+Vt+ℜtr0‖)是QP′的单位向量.下文将讨论不同运动状态对应的频移解析式.考虑点O相对于雷达的方位角和仰角分别为α 和β,则点O在雷达坐标(U,V,W)中位于(R0cosαcosβ,R0sinαcosβ,R0sinβ),雷达视场的单位矢量变为

假设振动目标在时间t0=0 处的散点P在参考坐标系(X,Y,Z)中位于(X0,Y0,Z0)T,则经过时间t后移动到:

散射体P由于振动而产生的速度变为

则振动目标的微多普勒频移[16]写作:

当方位角α 和俯仰角βP均为0,(7)式可写作:

其中,f为载波频率,fv为振动频率,Dv为振幅.假设 ‖R0‖≫‖Vt+ℜtr‖,n=R0/‖R0‖,(3)式可近似写作:

式中第1 项是由平移引起的频移;第2 项表征旋转引起微多普勒效应,即

由于目标的旋转,在局部坐标系(x,y,z)中描述目标上的任何点都将移动到参考坐标系(X,Y,Z)中的新位置.新位置可以通过其初始位置向量乘以由欧拉角 (ϕ,θ,ψ) 确定的初始旋转矩阵来计算,初始旋转矩阵写作:

其中,

在局部坐标系中观察,目标以角速度ω绕其轴x,y和z旋转时,位于r0=(x0,y0,z0)T的散点在局部坐标中表示的将移动到参考坐标系中的新位置,光程为ℜInit·r0,旋转的单位矢量变为

设标量角速度Ω=‖ω‖,t时刻旋转矩阵变为

在参考坐标系(X,Y,Z)中观察到散射体P经过时间t将从其初始位置移动到新位置r=ℜt·ℜInit·r0.综上,(10)式可写作:

假设目标以角速度沿z轴翻滚的速度为ω=ωz(rad/s),从参考坐标(X,Y,Z)来看,目标的角速度ω′=ω·[a12,a22,a32]T,此时散射体移动到:

一般地根据(9)式,翻滚是一种含有速度、加速度和旋转频率的复合运动.目标在时间t的速度变为V=[Va11,Va21,Va31-gt]T:

其中,

翻滚状态下的微多普勒频移主要是由其旋转项引起:

2.2 仿真研究

上述几何解析关系式是基于将目标视作散点得到.本文利用上述理论模型,通过面元剖分的方式,结合相关物理域采用有限元分析法将每个面元上携带的微动信息叠加起来fmicro-Doppler=,i为面元数,以实现运动目标时间-频率关系的提取.通过研究FFTshift 函数对仿真数据集进行处理,验证不同运动锥体微动特性研究实验的正确性.该仿真的计算步骤如下.

步骤1添加相关物理域

为了更贴合实际探测,仿真采用基于射频场的电磁波频域模型来描述实验环境,假设发射高斯光束,则目标的回波散射场由下式构建:

其中,ω0为光斑半径,Ebgo为背景场,p0为探测位置,k为波数,且满足:

步骤2绘制目标

绘制顶点为原点,底部半径为2.3 cm、高度为7 cm 的圆锥体.

步骤3导入边界条件以及相关参数

包括引入边界条件、光源参数、探针类型、位置、旋转域、几何操作和环境属性等表征目标不同初始位置和运动状态,其他参数在表1 列出.方位角和俯仰角可以通过设置光源和相机获得[17].在设置完目标和入射光后,可以自动得到目标的被照射面元关系.如图1 所示,洋红色区域表示被照射面元部分,阴影部分表示被遮蔽面元部分,洋红色箭头表示入射光方向,黑色箭头表示运动方向.

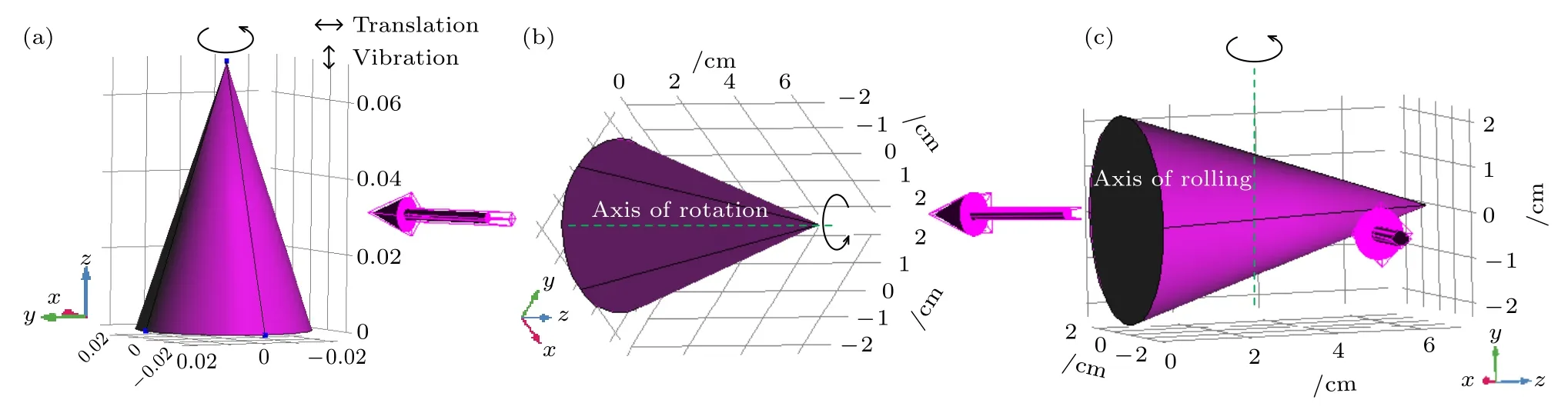
图1 多运动锥体和入射光的初始位置示意图 (a)自旋1/平移/振动;(b)自旋2;(c)翻滚Fig.1.Schematic diagram of initial positions of multi-motion cones and incident light: (a) Rotation 1/translation/vibration;(b) rotation 2;(c) rolling.

表1 不同位置上的频移和频谱宽度Table 1.Frequency shift and spectrum width at different locations.

步骤4导入公式和其他必要的几何运算

输入相应公式及相关参数.其他操作是指数据序列操作,包括空间投影、旋转轴和参考坐标系等.图2(a)—(c)分别对应图1(a)—(c)中各类运动的锥体目标在初始位置被照射面的投影,其中绿色虚线表示对称轴,红色虚线表示运动轴(旋转轴),如图2(a),(c)中被照射面的投影都是等腰三角形,但图2(a)中投影的对称轴和旋转轴共轴,图2(c)投影的对称轴和旋转轴不共轴.而图2(b)被照射面元的投影则是一个对称轴和旋转轴共轴的圆形.

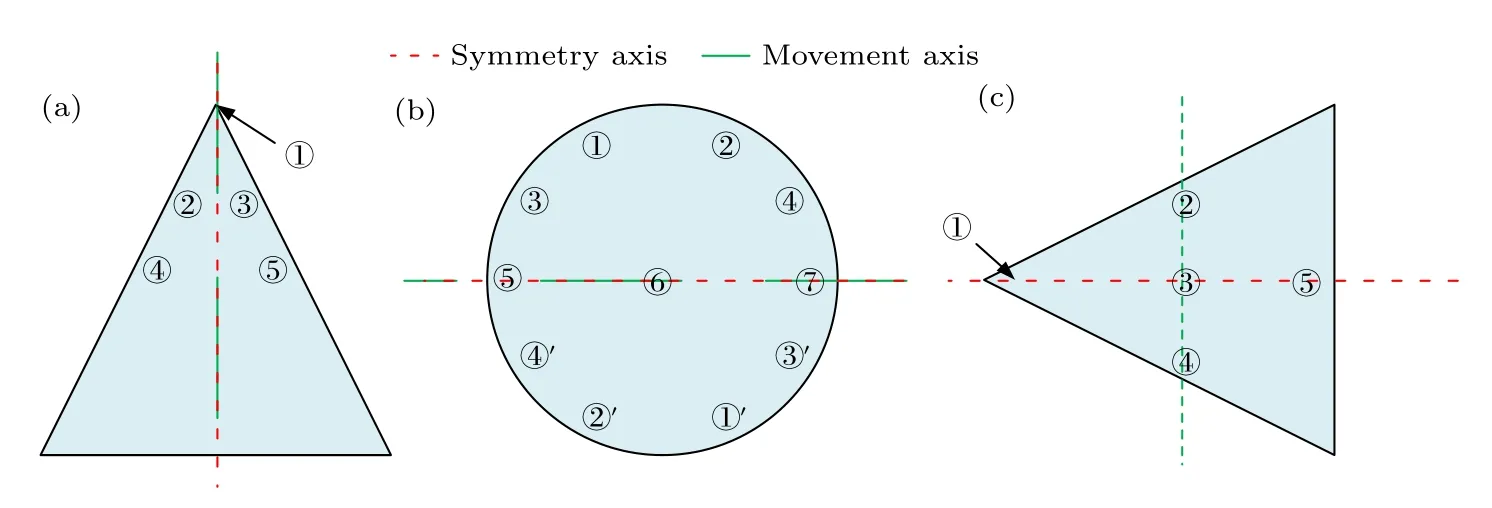
图2 多运动锥体运动初始位置的被照射面元投影 (a)自旋1/平移/振动;(b)自旋2;(c)翻滚Fig.2.Illuminated projection planes of initial positions of multi-motion targets: (a) Rotation 1/translation/vibration;(b) rotation 2;(c) rolling.

步骤5添加材料

目标材料为铝,无限空间材料为空气.目标材料和周围空气的引入能够自动导入影响目标反射特性和传输路径的相关参量[18,19],例如阻抗、比热率、电导率等.

步骤6网格划分和有限元求解

其能使用稳态求解器BiCGStab[20]解决解剖整体的复杂离散化问题.收敛次数为105,误差为10-11.

步骤7添加研究和绘图

展开频域扫描,得到如图3 所示顺时针自旋1目标上位置①,④,⑤的理论频移,用以验证后续一维微多普勒频移实验的正确性.图3(a)上①,④,⑤的频移分别为0.913 MHz,2.007 MHz和-1.965 MHz.不难发现,位置④的频移为正值,位置⑤的频移为负值.这两个点的频移值相对较大.而由于位置①位于对称轴上,因此频移值较小.

图3 图2(a)中顺时针自旋1 锥体位置①,④,⑤对应的频移Fig.3.Frequency shifts of the cone with clockwise Rotation 1 at positions ①,④ and ⑤ in Fig.2(a).

类似地,可以通过对(8)式进行时间t的参数化扫描获得振动目标的时间-频移关系.将得到的时间-强度数据利用FFtshift 函数能实现时间-频率-强度三者之间两两转换,从而得到如图4 所示的振动目标时间-强度关系的仿真曲线.不难看出,图4 的时间-强度曲线的包络是一条近余弦曲线.

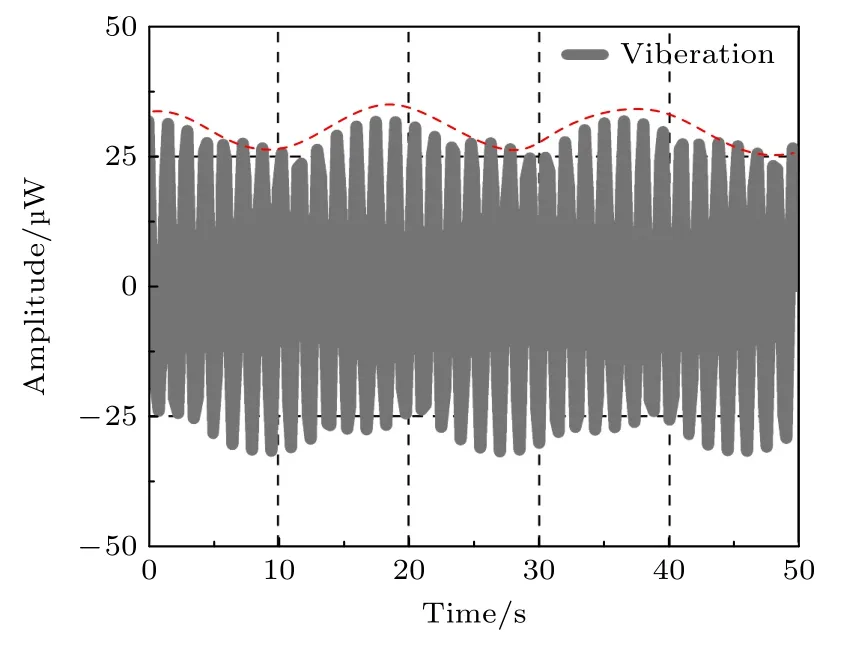
图4 振动锥体的时间-强度关系图Fig.4.Time-frequency relationship of a vibrating cone.

2.3 环境影响要素分析

一般来说,当电磁束穿过具有一定大气折射率时空统计分布的复杂系统时,由于自然或人为的影响,会受到不同程度的衰减、畸变和干扰,反映在回波信号的时间-强度分布上.因此,激光雷达的研究必须考虑发射和接收信号传播过程中的大气衰减.此外,实际探测条件比这些复杂得多,同时需要引入大气湍流模型来研究传输路径中的介质不均匀性[19].

2.3.1 大气衰减理论

通常,大气引起的激光衰减表示为

其中,I0是光强,λ 是波长,μ(λ)为大气衰减系数.常用的衰减系数预测经验模型为[21]

其中Vb为大气能见度,良好的能见度Vb=23 km,a是与可见度相关的波长校正因子.根据Koschmieder 公式,可推导出近地大气消光系数α(r)=3.912/Vb[22];大气透射率ηatm=exp[-μ(λ)].不同可见度下的不同波长校正因子如下:

2.3.2 大气湍流模型

回波的空间分布同样包括湍流引起的衰减.湍流的描述模型包括大涡模拟(LES)和雷诺平均Navier-Stockes (RANS).LES 用于计算非定常湍流,RANS 寻求平均意义上的流动结果.本文所涉及的仿真方法对这两个模型均适用.以RANS 方程中的一种典型模型——k-ε 模型为例[23],其瞬态传输方程可写作:

这里,F表征类似对流扩散的算子,k是对流和耗散(包括可选的稳定)的“刚度矩阵”,u2表征速度场,k2表示湍流动能,μ是动态黏度,ε 是耗散率.当温度变化很小时,ρ 为常数.表2 列出了其他参数及赋值.

表2 仿真中使用的大气湍流模型参数Table 2.Parameters used in numerical simulations.

本节将开展不同环境条件对目标回波特性影响的对比仿真实验.在2.2 节步骤1 中添加湍流k-ε 模型,图5 为顺时针自旋1 目标在不同环境条件下的强度分布及对应频移关系.对于收发同置雷达系统,设定光源和探测位置均为(-10,1,10).不同的天气条件具有不同的相对湿度、能见度,见表1.图5(a)表征晴天无湍流环境下探测顺时针自旋1锥体的回波强度分布以及时间-频率关系.自旋运动导致其强度分布呈“螺纹”状,因此,目标的强度分布图可用以反演目标的运动状态.利用FFT 得到对应的时间-频率曲线.该环境条件下的时频图是一条余弦曲线.

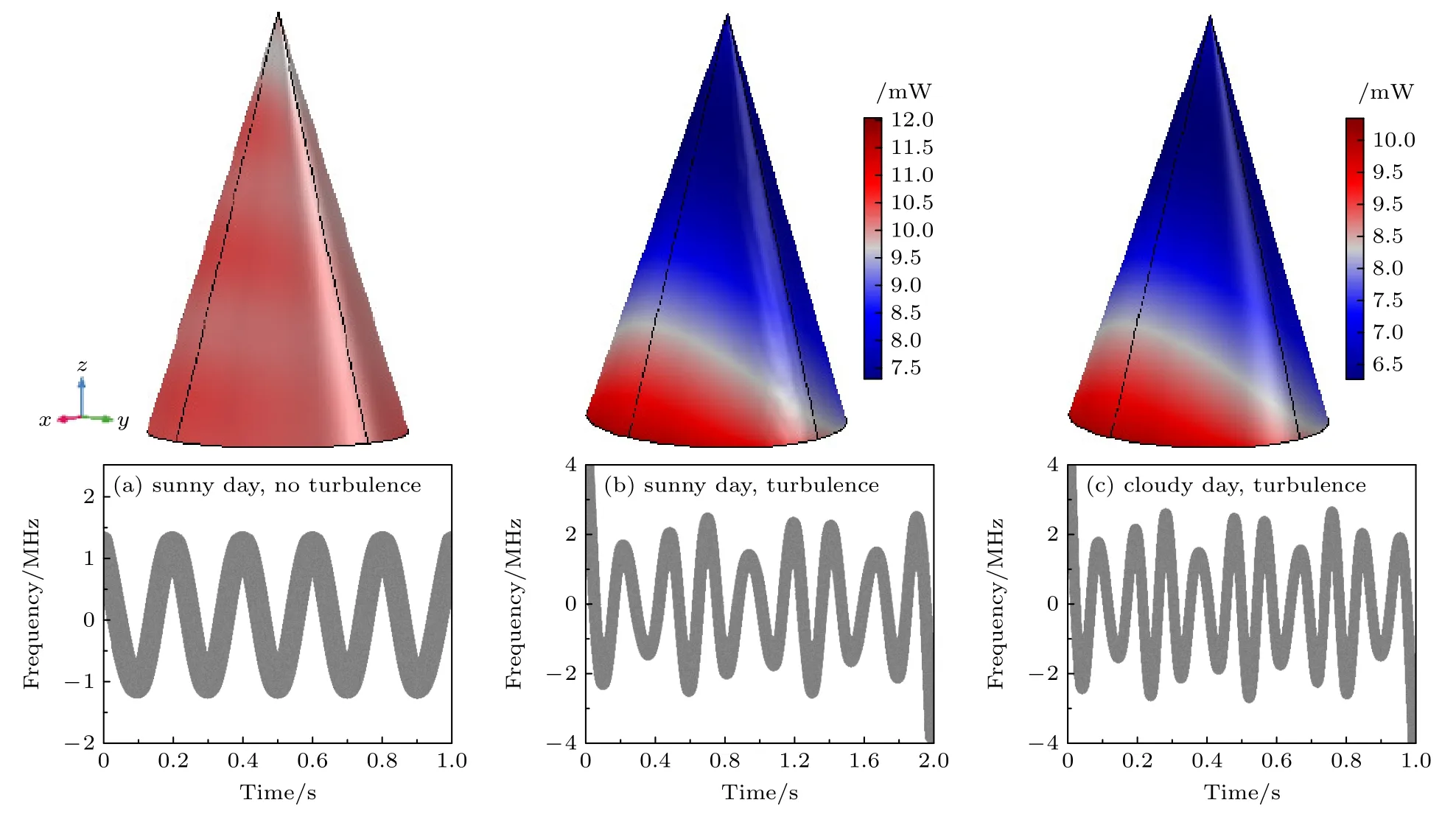
图5 不同环境条件下探测顺时针自旋1 锥体目标回波强度分布及时间-频率关系Fig.5.Echo intensity distribution and the relationship of time and frequency of a cone with clockwise rotation 1 under different environmental conditions.

图5(b)给出了晴天湍流环境下,探测顺时针自旋1 锥体的回波强度分布以及时间-频率关系.与图5(a)相比,由于湍流会改变传输路径介质的均匀性,因此其强度分布图也是不同的,与无湍流条件下的“螺纹”状强度分布图相比,湍流的存在使这种“螺纹”特征减弱,降低强度分布对运动状态的反演能力.由于大气湍流折射率的随机波动,波前相位畸变破坏了光波的时空相干性,光束漂移,导致该条件下的时频图是一条具有“频移变形”的类余弦曲线.变形的程度随着湍流强度而变化.

图5(c)表征阴天湍流环境下的强度分布及时频关系.由于能见度和相对湿度呈明显的反向[24]关系.对比图5(b),(c)可以得到相对湿度引起能见度和大气衰减系数的变化对强度分布并无影响,因此时频曲线的形状不变.根据(21a)式和(21b)式不难发现,大气衰减系数对目标反射信号的强度大小具有指数影响.阴天的回波强度低于晴天,导致时间-频率曲线的周期也变小.

一般来说,对于能见度较低的天气,要在一定程度上增大探测光强,即能够满足探测条件.但是能见度较低的环境条件通常伴随着湍流,这会改变传输路径的介质均匀性,从而影响被探测目标的波形.总体来说,对中远距离目标微动特性探测进行仿真模拟,能够通过分析环境因素的影响实现对回波特性的控制,有利于缩短激光雷达的研发周期,减小实际探测的资源消耗.

3 实验研究

针对晴天无湍流环境开展利用收发同置系统微多普勒效应室内实验研究的原理,如图6(a)所示.实验环境波长为1064 nm 的激光器发射的种子光被光纤分束器一分为二.光路穿过掺铒光纤放大器(EDFA)、中心频率为100 MHz 的声光调制器(AOM)、偏振控制器(PC)和隔离器.偏振控制器用于校正偏振状态.隔离器可以保持光的单向输入并避免自激振荡.光纤放大器可以补偿损耗.环形器是一种多端口非互易光学器件,可以在同一地址发送和接收信号.发射的信号从端口1 进入端口2 到达目标,回波信号被耦合进入端口2 再经过端口3 进入探测器.图6(b)是被测的自旋和翻滚目标及转台.目标是一个高7 cm、底面直径4.6 cm的圆锥体,光出射位置到目标的距离为15 cm.图7的电动位移台用于平移和振动目标的测量.位移台与电源相连,设置电压为7.7 V,计算得到目标的频率为9.315 Hz.旋转台通电后,遮光臂能够在一个运动周期内阻挡RPM (每分钟转数)探测器两次.探测器与示波器相连,即可以通过信号周期计算旋转频率.为了更好地研究微多普勒效应,以被照射面元的整体大小是否随时间变化作为判定依据对不同运动进行分类: 以绕轴自旋为例,被照射面元的整体大小不随时间变化,因此不同目标位置的微多普勒频移基本上是时不变的,这种类型的运动被称为频移时不变运动;而振动、翻滚和平移目标的被照射面元整体则随着时间变化,即频移时变运动.为了更好地研究目标上不同位置的微多普勒频移变化,入射方向相较于水平地面有一个2°的夹角.

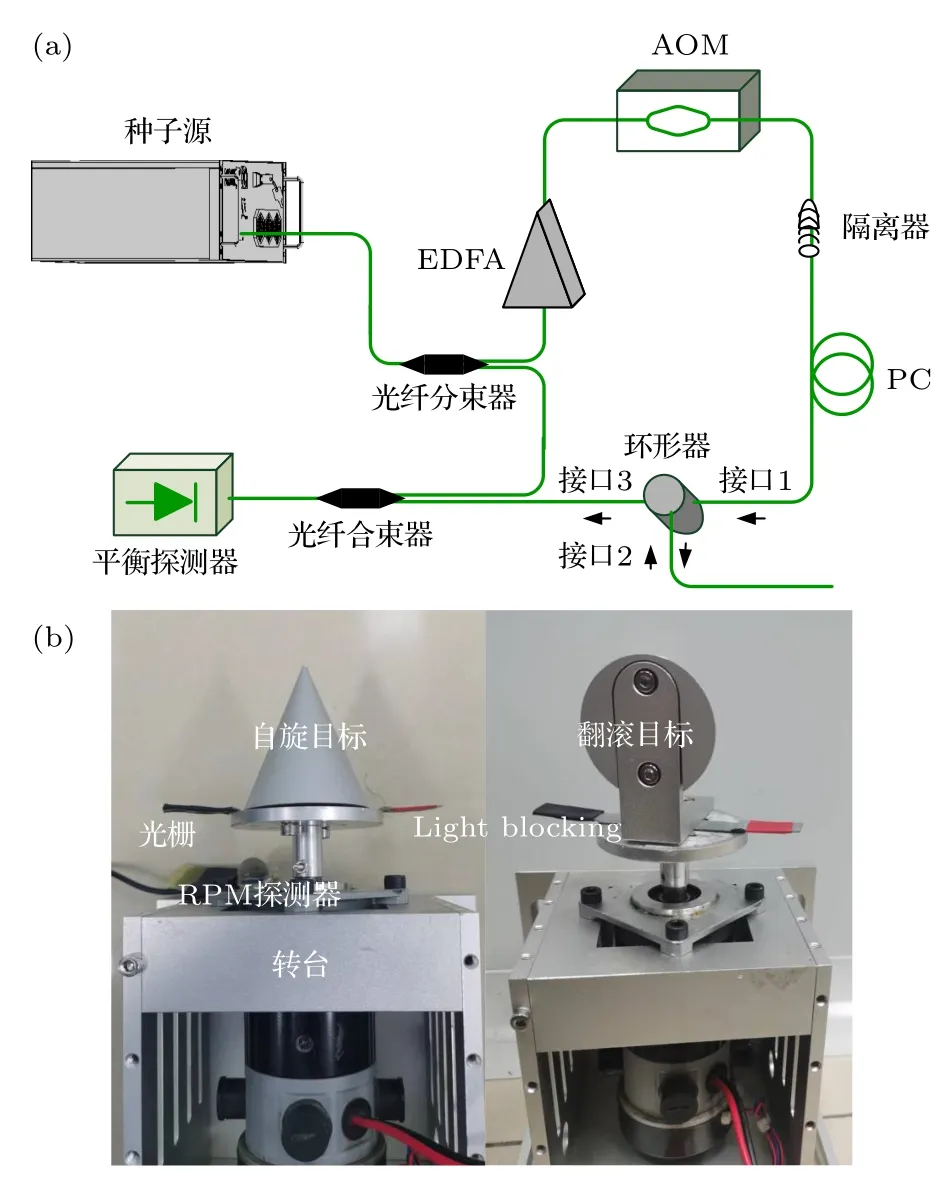
图6 运动目标微多普勒频移实验装置图Fig.6.Device for measuring the micro-Doppler frequency shift of moving targets.

图7 电动位移台Fig.7.Electric moving stages.

3.1 频移时不变运动目标的微动特性

首先,以图1(a),(b)的频移时不变运动目标自旋1 和自旋2 锥体为例开展微多普勒效应的研究.示波器探测得到的时域关系利用FFT 操作再与中心频率比较,即可得到如图8 和图9 所示自旋锥体上不同位置的频移.图8 为自旋1 锥体上不同的频移.频移曲线包络的近似为直角三角形.图8(a)—(c)为顺时针自旋1 锥体上位置①—⑤的频移,其频移曲线包络为斜边在左的直角三角形.实际探测位置①的频移为0.547 MHz,位置④的频移为1.549 MHz,位置⑤的频移为1.656 MHz.实验结果表明,锥体目标上的位置越低,两侧的频移差就越大.这与图3 仿真的结论不谋而合.图8(d)—(f)为逆时针自旋1 锥体上位置①—⑤的频移,其频移曲线包络为斜边在右的直角三角形.综上可以发现,频移的包络形状能够反演出目标的运动方向.

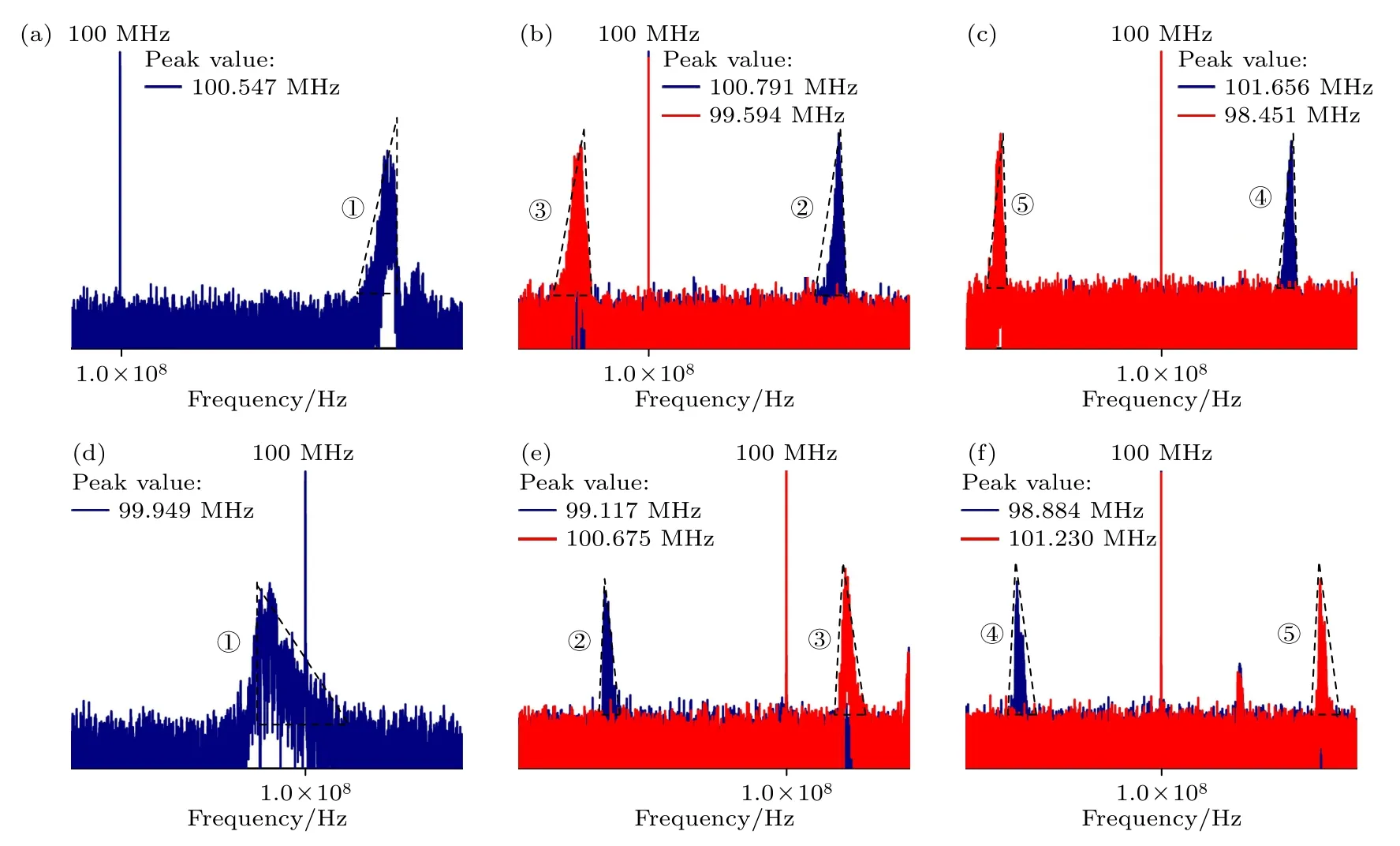
图8 自旋1 锥体上位置的频移示意图 (a)—(c)顺时针自旋1 锥体上位置①—⑤的频移;(d)—(f)逆时针自旋1 锥体上位置①—⑤的频移Fig.8.Diagrams of micro-Doppler at different positions of the cone with rotation 1: (a)—(c) Frequency shift of a cone at positions①—⑤ with the clockwise rotation 1;(d)—(f) frequency shift of a cone at positions ①—⑤ with the counterclockwise rotation 1.

图9 为顺时针自旋2 锥体上位置①—⑦的频移,这些位置的频移和谱宽等信息在表3 列出.其中,位置①和②处的频移值为正,位置①'和②'处的频移值为负.在位置③,④和④',③'处,频移为一正一负,不难发现,互为轴对称位置的频移正负性也相反.位置⑤—⑦位于对称轴上,而这些位置的谱线包络形状是几乎相同的等腰三角形.理论上,位于图2(b)圆周上的位置应该具有相同的频移量,而入射夹角的引入使这些频移量稍有不同,但这并不影响实际测量频移的变化趋势.另外,在中心轴位置的频移值和频谱谱宽相对较小,而在圆的外圈的频移值和频谱宽度较大.综上所述,将微多普勒频移和目标的形状特征联系起来,即得到频移的正负性,包络形状和谱线宽度都有助于反演目标的形状特征和运动特性.

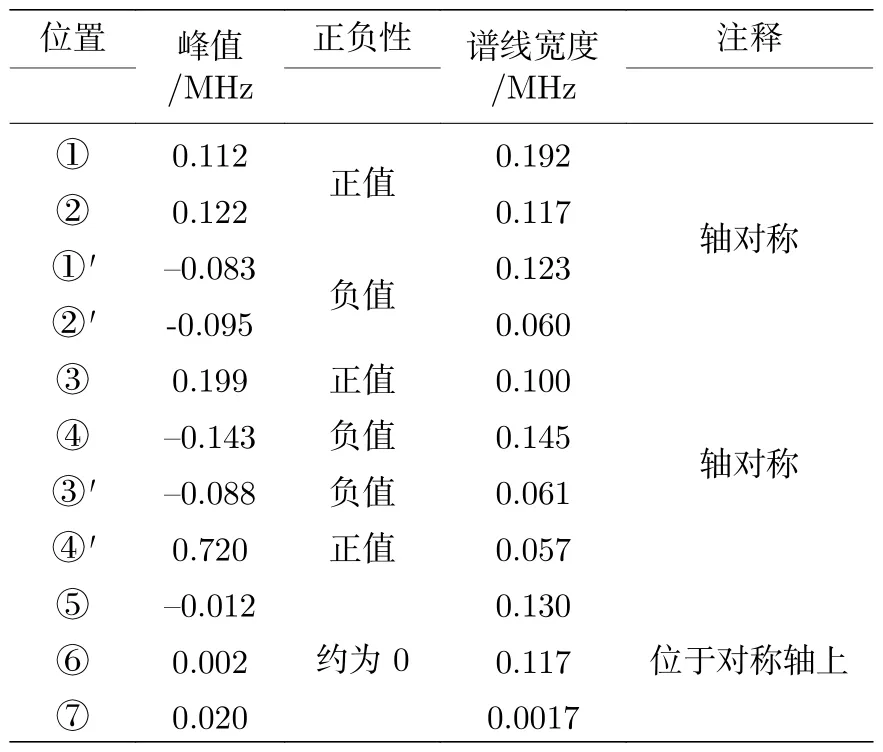
表3 不同位置上的频移和频谱宽度Table 3.Frequency shift and spectral width at different positions.

3.2 频移时变运动目标的微动特性

振动、翻滚和平移都属于频移时变运动.振动和翻滚是频移随时间周期性变化的运动,即周期性频移时变运动,应研究这类运动目标在一个周期中频移幅度的最高值、最低值和中值对应的3 个时刻.设振动幅度约为0.4 cm,振动频率为1.05 Hz.在一个振动周期内频移如图10 所示,频移谱线包络形状为三角形.

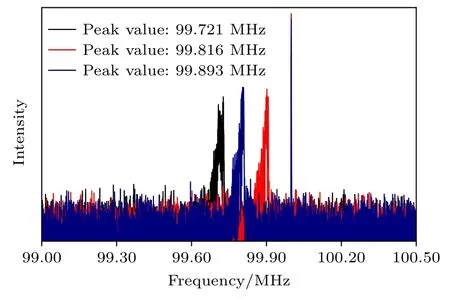
图10 振动目标上图2(a)中位置①处一个周期内三个时刻对应的频移Fig.10.Frequency shift at three times in a cycle on position ①in Fig.2 (a) of a vibrating target.

设置翻滚频率为4.10 Hz.在图2(c)的①—⑤位置,一个周期内3 个时刻的频移如图11 所示.总体来说,顺时针翻滚的锥体频移包络形状是斜边在左边的直角三角形.逆时针翻滚的现象正好相反,这类似自旋1 的结论.但不同的是,由于可能存在位置①,②和④可能出现在翻滚过程中被遮挡的情况,此时对应的频移为0.因此,可以通过频移图像的对比推断出目标运动姿态.

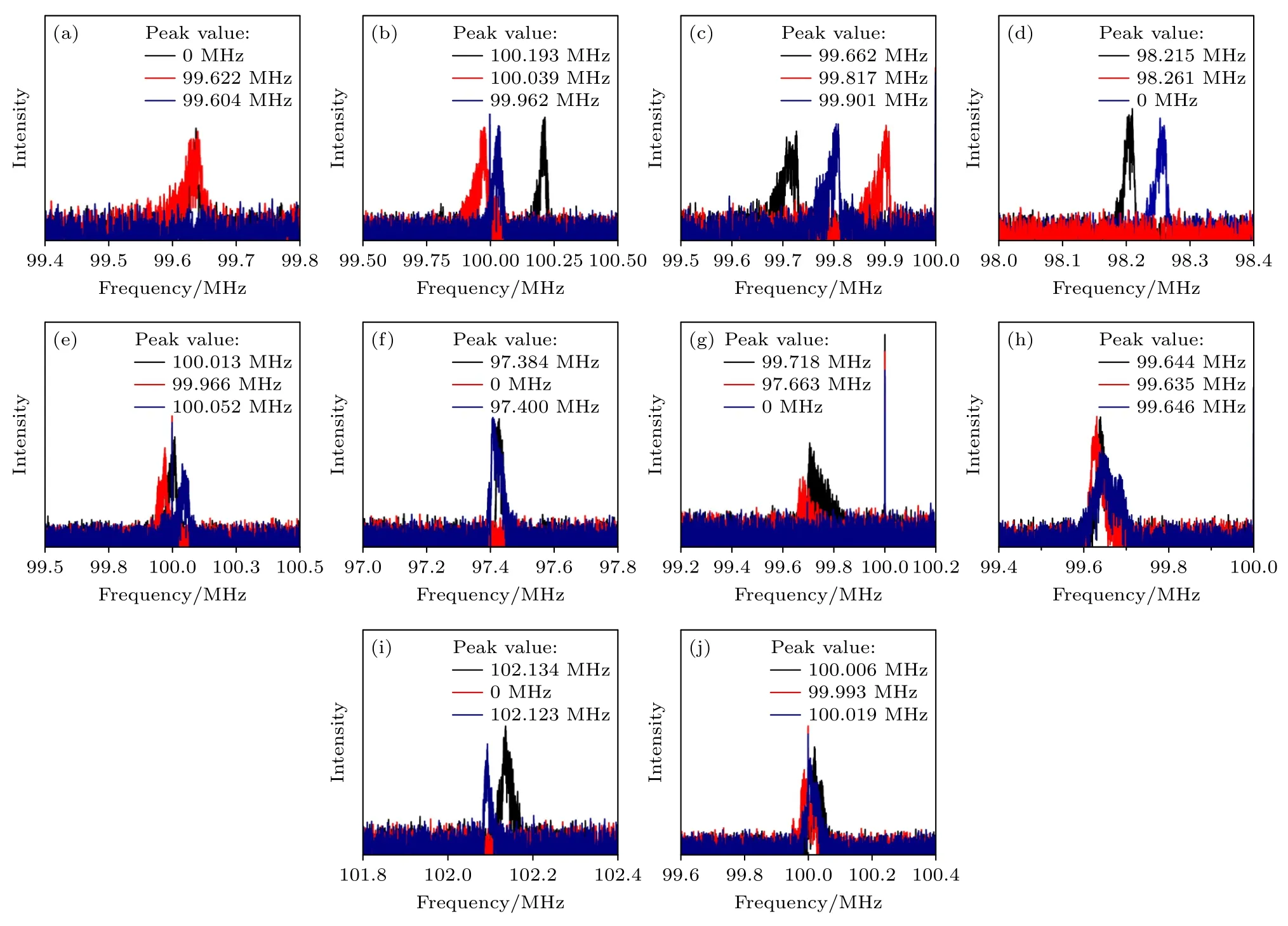
图11 翻滚目标不同位置的微多普勒频移图 (a)—(e)顺时针翻滚圆锥上位置①—⑤处的频移;(f)—(j)逆时针翻滚圆锥上位置①—⑤处的频移Fig.11.Diagrams of micro-Doppler frequency shift at different positions of rolling targets: (a)—(e) Frequency shifts at positions①—⑤ of a clockwise rolling cone;(f)—(j) frequency shifts at positions ①—⑤ of a counterclockwise rolling cone.

以图12 所示的平移为例,对应的微多普勒频移不随时间呈现周期性.假设目标远离探测器的方向是正方向.黑色表示目标正在靠近探测器以速度为V=-1 cm/s 移动,对应频移为负值.红色和蓝色线分别表示目标远离探测器以速度V=1 cm/s 和V=3 cm/s 移动,频移为正.平移的速度越快,频移幅度就越大.综上所述,可以得出关键的结论,即频移的正负值可以用来确定运动方向,频移的大小可以用来确定运动速度.

图12 匀速平移圆锥1 s 内的微多普勒频移曲线Fig.12.Curve of a translating cone with a uniform speed in 1 s.

利用FFTshift 函数对上述实验采集到的频率-强度离散数据点进行谱运算,可以得到目标时间-频率-强度参量之间的两两关系,从而实现运动目标多维度微运动特征的提取和分析.为了满足数据集的可被分割原则,设定采样频率为10 kHz,信号函数满足:

其中,A,B,X,Y,P,Q是常数.通过上述操作分别得到顺时针自旋1、顺时针自旋2、振动、顺时针翻滚和平移运动锥体的时间-频率-强度关系曲线,如图13 所示.很明显,不同的运动状态对应的三维信号时频强度[25]特征也具有着不同的谱线包络形状: 顺时针自旋1 的时强曲线包络类似余弦曲线;顺时针自旋2 和顺时针翻滚的信号曲线包络则都具有明显的三角形特征,二者存在着细微的区别;振动目标的时间-强度曲线包络是随时间变化的半圆形;平移目标的时间-强度曲线包络相对是一条直线.综上所述,时间-频移-强度三维关系曲线也可作为反演目标运动特性的重要工具.

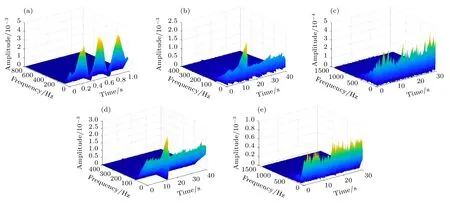
图13 不同类型运动锥体的时间-频率-强度三维关系图 (a) 顺时针自旋1;(b)顺时针自旋2;(c)振动;(d)顺时针翻滚;(e)平移Fig.13.Three-dimensional diagram of time-frequency-intensity relationship on diverse moving cones: (a) Clockwise rotation 1;(b) clockwise rotation 2;(c) vibration;(d) clockwise rolling;(e) translation.

4 结论

除了2.3 节中的环境因素,对比图3 和图8(a)—(c)不难发现,实际探测过程中由于传输过程和探测引起的衰减会导致实际频移幅度较小;通过对比图4 和图13(c)可以得到,由于实际测量中的噪声和光纤振动等不可控因素,使实际上探测的曲线包络较理论而言不均匀,且仿真曲线周期略大于实验周期.综上所述,客观因素(环境条件)以及人为因素(实验条件)会导致实验误差的产生.对于恶劣环境条件,应先通过对试验环境的仿真辅助控制探测功率,选择合适的波长以确保探测光的可接收性以及接收信号的准确性,此外可以通过相干探测满足对背景光的抗干扰能力,选择合适信噪比的种子源提升探测精度[26],固定光纤减少振动等方式降低人为因素带来的误差.

综上,本文在微多普勒效应解析法和电磁波频域模型的基础上,利用有限元分析开展三维目标时频关系模型以及讨论相对湿度、能见度以及有无湍流等环境条件对实验回波强度和时频关系影响.此外,定义了一种姿态分类方法,即将运动分为频移时不变运动和频移时变运动.频移时不变运动主要是两种类型的自旋,频移时变性运动主要为振动、翻滚和平移.利用收发同置探测系统,完成一维微多普勒频移信息的提取;根据FFT 函数实现运动目标的三维微多普勒时间-频率-强度之间的关系的建立.仿真和实验结果均表明,微多普勒是反演目标形状、运动类型、运动方向和运动速度的重要影响因素.这种多维参数处理的方法实现了对目标微动特征宏观信息的测量和微观信息的提取,为雷达探测和隐藏目标的精确识别和定位奠定了理论和试验基础.