二维旋转谐振子势中单粒子的跳频压缩及演化*

王渝 吴艺豪 李易璞 卢凯翔 伊天成 张云波

(浙江理工大学物理系,浙江省光场调控重点实验室,杭州 310018)

本文主要研究二维旋转谐振子势中单粒子的动力学行为,通过跳频的方式分析该粒子的压缩演化过程,并分析了相应的物理机制.一方面,研究跳频过程对回旋半径模式的压缩演化,通过选择适当的跳频时刻,分析跳频过程对压缩的影响.研究表明,回旋半径坐标的压缩程度并未在跳频时刻发生改变,但可在后续的演化中出现更强的压缩现象.另一方面,主要研究跳频过程中心导向模式的压缩演化.通过参数的选择,分析了两种压缩模式,即发散模式和振荡模式的压缩及演化.有趣的是,在中心导向模式压缩中,外势存在一个由旋转角速度决定的临界势阱纵横比.压缩模式在此处发生突变,且在振荡模式中,势阱纵横比趋于该临界值时,将出现明显的压缩.

1 引言

基于特定的外场实现微观粒子行为的调控一直是物理学领域的研究热点之一[1-3].外场的引入使得这些微观粒子自由度相互耦合,从而导致它们的原本运动轨迹和行为发生显著改变,甚至可能催生出奇妙的量子现象.例如,通过外部电场、磁场或光场来改变粒子的能级结构,实现粒子量子态的调控,使得出现量子态压缩等现象[4];通过冷却技术（激光冷却、离子阱等）可以降低粒子的温度,使它们进入更低的能级,从而表现出更明显的量子行为[5];通过引入拓扑绝缘体可以改变粒子的能带结构,引发拓扑量子相变,从而实现量子态的调控[6].对于这些现象的深入研究不仅能促进对量子体系中动力学行为的理解,还能为在量子信息与计算、量子精密测量等领域的应用提供重要的理论依据.

自1976 年Yuen[7]提出压缩态以来,此概念受到了诸多理论和实验物理学家的关注.在此后的几十年中,压缩态在量子光学、精密测量等各个领域中均取得了诸多重要的进展.至今,压缩态已经可以在各种物理系统中产生,包括电磁场[8]、自旋系统[9]、微机械振荡器[10-12]和单个捕获离子的运动模式[13,14]等,同时也得到了广泛的应用.例如,在精密测量领域,通过量子态的压缩可以实现更精确的测量结果,甚至可以探测到微弱的信号或现象,典型的应用如近年来的光学干涉测量、引力波探测等[15].同时,在原子钟的研制中,通过对量子态的压缩可以降低原子钟内的热运动和噪声,从而显著提高原子钟的精度和稳定性[16].此外,量子态的压缩还可以用于制备精密的量子传感器,如量子陀螺仪、量子加速计等[17].近年来,通过可逆压缩技术实现被测量信号的增强,从而实现弱信号的高精度测量在一些体系中也取得了成功.研究表明,在光学干涉测量术[18]和自旋系统[19]中,压缩相互作用的逆转可以增强较弱的相移信号,从而放宽探测的要求[20];在微波腔中,光子场位移也使用类似的相敏放大方案进行了增强[21,22].然而,该技术在机械振荡器系统中的实现仍存在一定困难[1].目前,如何通过压缩来进一步提高测量精度仍然是量子精密测量领域的挑战.特别是,通过设计特定的压缩方案来显著降低在实验探测过程中嘈杂的噪声,进而实现更高精度测量一直是该领域关注的焦点.

20 世纪90 年代左右,通过谐振子频率的变化产生压缩态的问题受到了广泛的讨论[23-31],其他与时间相关的振荡器也在文献[32-34]中被研究.相关研究发现,任何非绝热的频率变化均会导致压缩,且如Agarwal 和Kumar[31]所指出,在频率突变(跳频)的情况下,压缩将尤为明显.随后,Janszky 和Adam[35]发现压缩与跳频之间的时间间隔有很强的相关性,并证明一系列适时的跳频会导致更强的压缩.在谐振子中,产生压缩的速率通常是由量子速度限定的,而谐振子频率的突变可将基态投射到压缩状态,从而避免时间的约束.由此,Xin 等[36]于2021 年通过声光调制器来操控光学晶格中原子谐波振荡频率的跳变,从而创建了原子运动的压缩态,实现了谐振子跳频的快速量子压缩.该研究结果可以加快量子门的速度,并在嘈杂的环境中实现量子传感和量子信息处理.另一方面,Fletcher 等[2]通过使二维谐振子势场存在一定旋转的频率,在最低朗道能级中动态产生了占据单个朗道规范波函数的玻色-爱因斯坦凝聚体,并证明了轨道引导中心的几何压缩比标准量子极限低7 dB 以上.这一研究结果为实现强相关流体和玻色子量子霍尔态提供了一条新的途径.

目前,对于在旋转谐振子外势中,研究跳频导致的量子态压缩却鲜有报道.因此,本工作将在文献[2,36]的基础上,理论分析单粒子系统在旋转二维外势中的跳频压缩.对于具体的实验系统,我们设想可以首先从磁光阱中将冷原子系综装载到二维光学晶格,并对超精细态进行可分辨拉曼边带冷却从而制备出处于振动基态的原子[37].在谐振子势光阱装载冷原子的基础上通过调节光束的阱深(光功率、光束直径),或者改变光束(一般是高斯光束)的瑞利距离对囚禁势频率进行调节,对光束的调节可以在很快时间内实现跳频.

2 单粒子哈密顿量

考虑单个粒子处于匀速旋转的二维各向异性谐振子势阱的情况,若选取z方向为旋转轴,则在相应的旋转参考系中,系统的哈密顿量为[2]

3 回旋半径模式的压缩

回旋半径坐标主要描述该系统中朗道能级的物理量,本节主要研究将x,y方向频率互换的跳频过程对回旋半径模式压缩的影响,跳频时序如下:

根据海森伯运动方程,可得到以下独立的微分方程

相应的解为

根据回旋半径坐标的定义,可得其演化为

由于跳频过程主要使得粒子的哈密顿量在H+和H-转变,因此后续的两次跳频所满足的运动方程及其解的形式仍由(6)式和(7)式表示,选择β+τ2=π/2 以及β+τ3=3π/2 为第二、三次的跳频时刻,相应解的系数为

相应的涨落为

至此,关于各阶段回旋半径的压缩演化的解析形式已经得到.从上述公式中,不难发现跳频使得回旋半径的压缩演化发生了改变,来回的跳频也使得回旋半径压缩出现了交替演化的现象.接下来,选取特定的跳频时刻以及压缩参数进一步分析相应的物理现象.

2.1.3 复合菌剂对玉米根际土壤碱性磷酸酶活性的影响 不同施肥处理下，2个玉米品种根际土壤碱性磷酸酶活性在生育期呈现出：抽雄期>灌浆期>苗期>成熟期；抽雄期与灌浆期均呈现出金穗4号>先玉335，苗期和成熟期不同处理表现各异。抽雄期时，2个玉米品种表现为：B>C>A>D>E，处理B比A，E处理分别提高19.7%、53%(先玉335)和8.5%、31.9%(金穗4号)(图3)。

图1 展示了三次跳频下回旋半径涨落的演化过程.从图1 可以发现,在跳频的时刻回旋半径的压缩并未出现突变,但在后续的演化中出现了不同程度的压缩.同时,在多次来回跳频的过程中,涨落的演化也出现了在两种状态 {ωx,1,ωy,1,H+} 和 {ωx,2,ωy,2,H-} 中切换的现象.

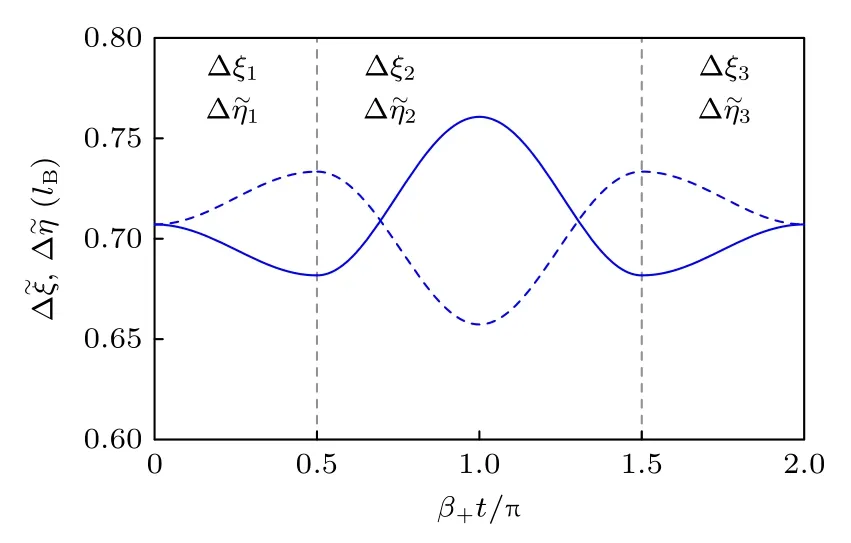
图1 三次跳频下回旋半径涨落随 β+t 的演化过程,其中ε=0.125 和 Ω/ω=0.9.实线和虚线分别表示 演化曲线Fig.1.Variances of cyclotron coordinates evolve with β+t under three frequency jumping,where ε=0.125 and Ω/ω=0.9.The solid and dashed lines respectively represent the evolution curves of .

4 中心导向模式的压缩

中心导向坐标主要是描述该系统中能级简并度的物理量,本节重点关注单次跳频对中心导向模式的压缩:

由海森伯运动方程可得:

其中,f(Ω/ω)=1+(Ω/ω)2-.容易看出,函数f(Ω/ω) 的符号决定了最终解的模式,且仅当 0＜Ω/ω＜时出现振荡解,相应的两个模式分布如图2 所示.图中的临界曲线即为f(Ω/ω)=0 时ε与Ω/ω满足的关系.从f(Ω/ω) 的表达式可以看出,在 0＜ε,Ω/ω＜1 范围内,|f(Ω/ω)|的取值均不超过 1.因此,β-的取值将无法超过系统频率ω 的限制,从而不会出现由于β-过大而导致的涨落随时间t高速振荡的情况.

图2 变量 (ε,Ω/ω) 中,两个压缩模式的相图Fig.2.In the variables (ε,Ω/ω),the phase diagram of squeezing modes.

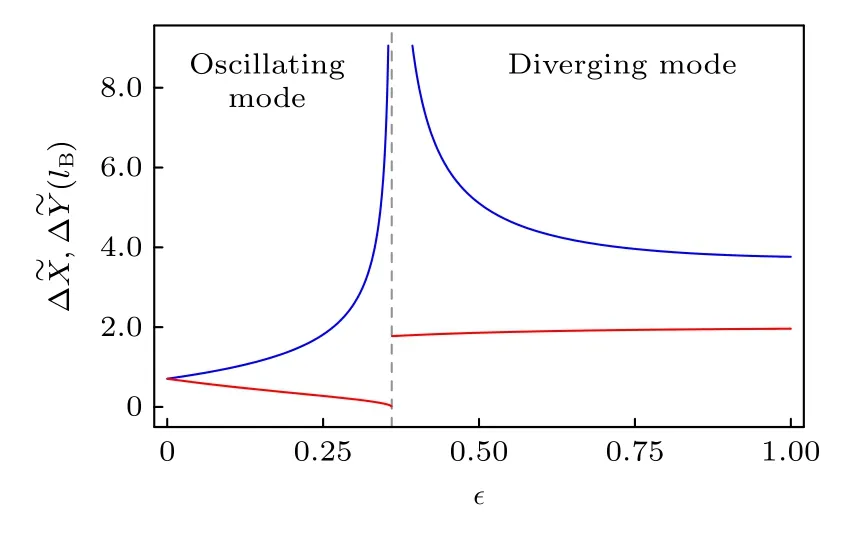
图3 中心导向坐标最大压缩量随 ε 的变化曲线,其中 Ω/ω=0.8.蓝线和红线分别为 和 的曲线Fig.3.Variances of maximum squeezing of guiding center coordinates change with ε,where Ω/ω=0.8 .Blue and red lines represent and .

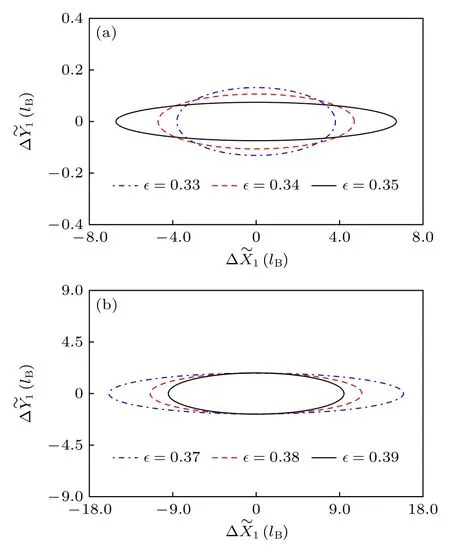
图4 中心导向坐标 和 在最大压缩量处的涨落 (a)振荡模式;(b)发散模式Fig.4.Fluctuations of guiding center coordinates andat maximum squeezing: (a) Oscillation mode;(b) divergence mode.

由上述分析可见,对于中心导向模式,跳频过程并不在跳频时刻改变压缩,同时也不改变相应的压缩模式.因此,这里可设置跳频时刻τ=0,并直接分析跳频后的演化过程.对于 {ωx,2,ωy,2,H2} 的情况,相应的通解为

其中,对于发散模式和振荡模式的系数都为

类似地,中心导向坐标可表示为

其中,对于发散的情况,

相应的涨落为

对于振荡的情况,

相应的涨落为

5 结论

本研究聚焦于二维旋转谐振子外势中单粒子回旋半径坐标和中心导向坐标的涨落压缩现象,旨在深入探讨压缩过程的物理机制.通过对单粒子的跳频分析,首先观察了回旋半径模式的压缩演化.通过合适的跳频时刻的选择,揭示了跳频对压缩的影响,尤其是在后续演化中可能引发更明显的压缩效应.结果表明,回旋半径坐标的压缩程度在跳频时刻并未显著改变,但在后续演化中,压缩效应得以显著增强.另一方面,本文还着重研究了中心导向坐标在单次跳频过程中的压缩演化.通过适当选择参数,成功识别了两种不同的压缩模式,即发散模式和振荡模式,并揭示了它们背后的物理规律.值得说明的是,研究发现外势存在一个由旋转角速度决定的临界纵横比,这对中心导向坐标的压缩模式产生显著影响.在振荡模式中,当外势纵横比趋近于这一临界值时,压缩效应显著增强,呈现出明显的突变.这一发现不仅丰富了对谐振子外势中压缩现象的理解,还为进一步探索量子传感等应用提供了有趣的线索.

附录A

这里给出(1)式通过幺正变换G=e-iκxy(mω/ℏ)至(2)式的推导,即计算H=GHlG†.首先考虑如下对易关系:

因此可以得到,

类似地,

同理,有

同时,对于Lz的变换为

此外,有

将上述变换结果分别代入H=GHlG†,即可将(1)式变换至(2)式.