基于神经网络的粒子输运问题高效计算方法*

马锐垚 王鑫2) 李树 勇珩 上官丹骅†

1) (北京应用物理与计算数学研究所,北京 100094)

2) (中物院高性能数值模拟软件中心,北京 100088)

蒙特卡罗方法是求解粒子输运问题的有力工具之一,其局限性在于为达到精度要求需模拟大量粒子,计算耗时长,这阻碍了该方法的进一步应用,尤其在需快速响应的情形.本文结合神经网络和若干蒙特卡罗方法基本原理发展了一种计算方法,能够实现源分布可变,几何、材料和目标计数不变的中子输运问题的快速准确求解.首先,为高效生成用于神经网络训练的数据,利用重要性原理实现在同样模拟次数基础上有效扩充训练数据集容量,在一定程度上克服了使用蒙特卡罗计算获取训练数据耗时长的缺点.进而,基于目标计数是源分布与重要性函数乘积积分的事实,设计了利用神经网络实现快速输运计算的策略.该网络的输入是中子源项,输出是目标计数,在几何、材料和目标计数固定的情况下,该神经网络可重复使用,根据新的源项快速准确得到目标计数.本文所提出方法的原理和框架同样适用于其他种类粒子的同类型输运问题.基于若干基准模型的验证表明,训练得到的神经网络能在不到1 s 的时间内得到目标计数,且与蒙特卡罗大样本模拟得到基准结果的平均相对偏差均低于5%.

1 引言

蒙特卡罗(Monte Carlo,MC)方法和确定论方法是求解粒子输运问题的两类主要方法[1].随着核技术的发展,各类新型核设施具有更复杂的几何结构和反应机制,各向异性更强,同时对计算精度的要求也在不断提高.为解决这类复杂粒子输运问题,在计算机硬件性能不断提高的基础上,MC 方法由于能够对物理过程和几何构型进行精确建模且并行效率高,因此得到广泛的发展和应用[2].同时,pin-by-pin 反应堆模型输运[3]、复杂多物理场耦合计算[4]等大规模精细模型快速计算要求也在不断推动MC 方法相关研究的开展[5].由于MC方法求解目标计数的相对误差与样本数平方根成反比,而计算时间与样本数成正比,为使误差达到要求,其模拟过程非常耗时[3,6-8].国内外研究团队已发展多种减方差方法[9-19],目标是以较少的样本数达到更低的统计误差.权窗算法是其中重要的一类,一般认为比几何重要性等算法效率更高,其算法参数可由重要性原理产生.重要性原理最早由Booth 和Hendricks[14]提出,网格的重要性定义为进入该网格的单位权重的粒子及其后代对计数器的总贡献.虽然存在大量研究,但MC 输运的绝对计算时间仍然相当可观,且各种减方差方法的适应条件不同,在应用上有一定的局限性.

深度学习中的神经网络是一种高度并行的信息处理系统,具有很强的自适应学习能力,能处理复杂的多输入、多输出非线性系统[20-23],训练完成的网络可根据输入快速输出目标值[24-27],在诸多领域有广泛应用[28-32].近年来,在核相关领域利用数据驱动的神经网络进行中子输运计算的趋势日益明显.Berry 等[33]研究利用人工神经网络和随机森林分类器评估给定能群结构的适用性,以准确预测轻水堆中的中子倍增因子.Cao 等[34]提出基于神经网络的重构中子场方法,用于重建反应堆压力容器和堆芯区域内的中子场.Zhang 等[35]提出一种基于神经网络的源项重建方法,实现复杂的三维源项快速重建.张海明等[36]建立了基于卷积神经网络的深度学习模型,可用于直接预测反应堆堆芯有效增殖因子.针对多组分中子屏蔽材料优化设计中MC 模拟计算时间长的制约问题,林海鹏等[37]讨论了利用神经网络算法快速预测不同材料中子屏蔽效果的方法.Osborne 等[38]通过上采样方法实现从少量粒子数MC 模拟结果到精确结果的映射.Kim 等[39]构建了一个以堆芯结构为输入的神经网络,可快速优化堆芯结构设计.与其他类型粒子输运结合的研究,主要是在医学图像处理以及人体剂量学领域[40-42].

在上述数据驱动的神经网络应用中,网络通过分析所提供数据集的模式和输入输出之间的映射关系来学习和进行快速预测,因此训练数据集的数量和质量对网络的鲁棒性和有效性有很大影响,而训练数据的获取通常采用MC 模拟或其他数值计算方法得到,难以避免大量计算时间和计算资源的消耗.对于数据驱动型的神经网络,如何利用神经网络代替特定问题的传统计算,以及如何利用传统方法高效获取训练数据都具有重要的研究意义.

本文的研究对象是源分布可变,几何构型、材料和目标计数不变的问题,目标是在结果合理的前提下提高计算速度.这类问题在国防科技和国民经济领域存在多种应用场景.例如,中子输运是战略国防科技研究所必须的多物理耦合计算中最消耗计算资源的一环,计算时间可以占总体时间的90%以上,在装置变化缓慢阶段,可认为每一步中子输运的源项都有变化而装置的几何、材料变化可忽略不计,因此呈现为变源问题;在民用经济方面,反应堆高置信度数值模拟需要快速计算压力容器的中子注量率,而反应堆构型复杂、尺度大的特点导致其求解非常耗时,且工况复杂、燃料布置方案多样,以堆芯整体为源项进行模拟计算时是典型的变源问题,面临着快速求解难题;另外,变源问题的快速实时求解也是为“脏弹”恐怖袭击的科学预防提供备选方案的重要技术手段.

本文的主要贡献和创新之处在于: 1)以高效产生训练数据为目标,从重要性的定义出发,首次将其应用在等效MC 计算的训练样本生成中,发展出神经网络训练数据高效生成方法,达到在同样模拟次数基础上有效扩充训练数据集容量的效果.2)基于目标计数是源分布与重要性函数乘积积分的事实,构建可重复使用的高效神经网络,以快速准确获得各种源分布对应的目标计数,一定程度上突破了传统MC 输运计算的效率瓶颈.虽然本文的研究对象是中子,但该方法可适用于其他种类粒子的同类型输运问题中.

2 方法介绍

本文建立了一种利用神经网络加速MC 模拟中子输运问题的方法(图1 为技术路线图),该神经网络所必需的训练数据集是通过对相应的输运问题进行MC 模拟而获得的.对于新的中子源分布,将其输入给训练好的神经网络就能快速输出相应的目标计数.数据驱动的神经网络需要足够的高质量训练数据,但通过传统的MC 模拟来获取这些训练数据非常耗时.针对这一问题,将重要性原理作为一种高效生成训练数据的手段,由此在一定程度上提高了神经网络的训练效率.

图1 本文技术路线图Fig.1.Study framework of this paper.

2.1 理论基础

对于中子固定源问题,统计体通量、能量沉积、剂量等物理量都与源项信息直接相关,其中源项信息包括位置分布、能量分布、粒子发射方向等多维信息.中子的属性用p=(r,E,w) 表示,其中r表示粒子空间位置,E表示能量,w表示发射方向.中子源分布满足归一条件:

MC 模拟中目标计数可以表示为

其中,S(p) 为源分布,g(p) 为重要性函数.将相空间Ω进行网格划分,即Ω=(M足够大,表示划分足够精细),当源分布所在相空间划分足够精细的假设成立时,相空间内单个网格的重要性函数可以用该网格内一个点的重要性函数表示,则(2)式可被表示为

对于固定源问题,同一个模型(包括几何及材料)和目标量对应同一套,对于不同的源分布,将S(p) 离散化为代入(4)式,即可得到计数I.

本文以体平均通量作为目标计数(相同方法可适用于任何计数).对于不考虑时间变量的固定源问题,定义

其中,Ψ(r,w,E) 是中子角通量密度,则体平均通量可以被表示为

ΦV可以通过径迹长度估计法计算,粒子一旦通过计数区域就会对目标计数造成贡献,一般而言较其他估计法效率更高,因此被多数MC 输运程序采用.

2.2 基于神经网络的粒子输运问题高效计算方法

对于源分布多变,几何、材料构型及目标计数稳定的一系列中子输运问题,MC 模拟可看作一个黑箱,其输入是源分布,输出是固定的目标物理量,这个黑箱通过精确度很高,但是速度较慢的模拟将输入转换为输出.通过设计合适的神经网络并以合理的形式表示输入端的源分布函数,在获得充足的训练数据基础上,训练得到的神经网络将以很快的响应速度得到新的中子源分布对应的目标物理量.

在实际应用中,难以实现将连续形式的、不同分布的源项处理为神经网络的统一输入形式.为了解决此问题,本文首先对源分布进行N次采样,从而产生N个源粒子.然后将这些粒子的六维属性(r,E,w)作为点分布输入网络.最终网络产生N个输出的平均值被视为目标统计量的估计值.

为实现上述目标,将源分布在相空间离散化处理,进而以(4)式表达目标量后,可用训练得到合适的神经网络模型代替(4)式中权值,方法和网络结构示意图如图2 所示.本文采用多层感知神经网络(MLP)[21]的模型结构.神经网络中单层感知器的拟合能力有限,而多层感知器的拟合能力更强,可用于解决复杂问题,因而MLP 的优势在于它可以学习将任何输入映射到输出的权值.最典型的MLP 由三个网络结构组成: 输入层、隐藏层和输出层.本文使用的网络包括一个输入层、多个全连接层和一个输出层.在全连接层之间加入了整流线性单元 (ReLU)激活函数,激活函数为网络引入了非线性特征,有助于网络学习输入和输出之间的复杂关系,并能将神经元的输出限制在一定范围内.常用的激活函数包括Tanh,Sigmoid和ReLU,ReLU 的优点是能有效缓解梯度消失问题,从而提高训练效率.各层之间还引入了一个dropout 层,以减少过拟合,提高神经网络的泛化能力,使其更加稳健和精确.

图2 用于代理加速MC 模拟的神经网络结构Fig.2.Data-driven neural network for Monte Carlo simulation.

神经网络需要大量高质量的训练数据,以减少过拟合和网络泛化性不足等问题.然而通过MC模拟生成如此大量的训练样本必定成本高昂.因此,本文提出了一种基于重要性原理[14]的方法来高效获取足够的训练数据,此方法可在单次MC模拟中获取尽可能多的训练数据.重要性原理最早由Booth 和Hendricks[14]提出,用于输运计算中的权重窗参数生成算法.在本文中,重要性不再是作为生成权重窗参数的基础,而是作为相应网格中的源对目标计数的最终贡献,从而扩大了从单次算例模拟中获得的网络训练样本的数量.具体说明如下: 将相空间划分为网格时,网格i的重要性定义为通过该网格的粒子在单位权重下对目标计数的贡献.

当Ω空间内网格划分足够细时,对Ωi内的点pi与其所在网格内定点距离足够近,则有

上述方法在开源软件OpenMC[43]中得以实现.对于每个网格,定义了两个新的向量,分别记录网格的总权重和总计数.对于每个粒子,都定义了一个新的向量来记录粒子在整个轨迹中每一步所穿过的网格以及当前的权重.当前粒子被杀死时,记录的网格和相应的权重会被累加到对应网格的总权重向量中.此外,如果粒子被判定已到达最终统计区域,当前粒子的权重将被累加到它(及其子代粒子)穿过的所有网格的计数向量中.当所有源粒子及其次级粒子的模拟结束后,根据(7)式计算所有网格的重要性.

3 结果与讨论

3.1 重要性原理产生数据的正确性验证

为验证重要性结果计算的正确性,建立简单几何算例: 几何为10 cm×10 cm×10 cm、材料为56Fe的正方体.源项为位于坐标(0,0,0)的中子点源,发射方向为沿X轴正方向的单一方向,能量为10 MeV 的单一能量.在几何相空间划分0.1 cm×0.1 cm×0.1 cm 的虚网格,统计目标区域探测器(1 cm×1 cm×1 cm)的通量计数.分别建立10 个探测器,其中心位于X轴的不同位置.本数值实验基于相空间内一个点源的在进行MC 模拟的同时统计重要性结果,重要性结果取源项所在网格的重要性值,即以该网格为源对目标区域产生的目标值贡献,验证MC 计算结和重要性结果如图3 所示.由重要性值的定义可知,本算例中重要性的统计过程为由该相空间网格内的此点源产生的样本对目标区域的贡献除以总粒子权重,而针对这一点源MC 模拟同样为统计由此点源产生的目标结果除以总粒子数的平均值,因此对于此验证算例重要性与MC 模拟结果完全一致,说明本研究在OpenMC中重要性数据产生方法实现的正确性.

图3 重要性结果和MC 模拟结果对比(MC-MC 计算结果,IMP-重要性原理计算结果)Fig.3.Comparison of results of MC simulation and importance data (MC-results of Monte Carlo simulation,IMPresults of importance data).

3.2 神经网络结果验证

3.2.1 简单模型

基于3.1 节所设置简单算例对网络进行训练和测试.相空间网格的划分参数如表1 所列.在相空间中随机生成1000 个MC 算例(每个算例都是不同的点源),每个算例模拟106个粒子,以确保结果的最大统计误差低于5%.同时,用重要性生成方法计算生成1000 套重要性数据及统计误差,以重要性结果的统计误差小于2%为标准选取重要性数据,使用传统MC 模拟计算1000 个算例仅能产生1000 个源项及其目标统计量作为神经网络的样本,即训练集容量为1000,使用本文提出的基于重要性原理的高效训练数据产生方法后,在1000 个算例获得MC 模拟结果的同时产生了24285 个重要性数据,均可以视为该网格中点源产生的目标统计量,即将1000 次模拟得到的训练集容量提升了24 倍,显著提升了单次模拟获得的训练样本数.分别采用以下两组数据作为数据集对神经网络进行训练和测试: 1)仅采用1000 个算例MC 模拟的结果;2)结合重要性数据和MC 模拟结果.预测通量与真值的相对偏差被用作损失,并按(9)式计算:

表1 简单模型相空间划分参数Table 1.Phase space meshing parameters of the Fe model.

其中,x是作为真值的MC 计算结果;y是网络预测的通量结果.

神经网络的构建和计算使用TensorFlow[44]实现.采用自适应学习率优化算法Adam[45]作为优化器,学习率为10-4.Adam 优化器的优势在于无需手动调整,能根据每个参数的梯度和动量变化来调整其学习率,可以纠正其学习率消失、收敛过慢或是高方差的参数更新导致损失函数波动较大等问题.

图4 显示了网络训练过程中的损失函数曲线.在每个网络的训练测试中,80%的数据集用于训练,10%用于验证,10%用于测试.当基于验证数据的损失开始增加时,即终止训练.两个网络分别在5000 和10000 个算例时终止训练.最终网络输出结果与MC 计算给出的真值的相对偏差分别收敛到19.75%和0.97%.这表明,采用重要性原理补充数据集可以使网络更好地收敛.

图4 网络训练损失曲线 (a) 使用 1000 个MC 模拟结果样本进行训练;(b) 结合重要性数据和MC 结果进行训练Fig.4.Network training loss curves: (a) Trained with 1000 results samples of MC simulation;(b) trained with a combination of importance data and MC results.

对MC 模拟和神经网络预测的时间耗费进行了比较.在MC 模拟中,模拟106个粒子以确保统计误差保持在5%以下,使用1000 个实例的平均时间作为MC 模拟用.将1000 个算例输入已训练好的神经网络,并计算平均预测时间作为神经网络用时.结果表明,神经网络将计算时间大约从70 s减少到0.3 s,这意味着计算用时减少了约200 倍,显著提高了计算速度.

3.2.2 Kobayashi 模型

使用Kobayashi 模型[46]中的问题1 测试了本文所提出的方法.该模型包括三个区域: 源区域、真空区域和屏蔽区域(图5).X=0 和Y=0 平面是该模型的两个反射面.该例题给定单一截面,则仅在几何和角度维度进行相空间划分,划分参数如表2 所列.

表2 Kobayashi 模型相空间划分参数Table 2.Phase space division parameters of Kobayashi benchmark.

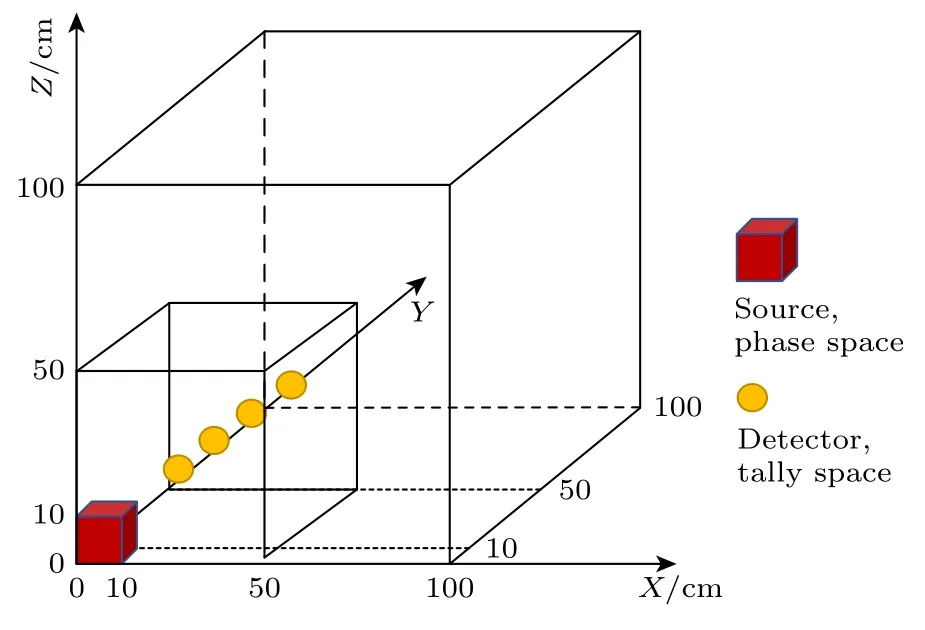
图5 Kobayashi-1 模型几何示意图Fig.5.Diagram of Kobayashi-1 benchmark.

该 Kobayash 问题一的基准包括两套不同截面设置: 在 Kobayash-1-i 中,源区和屏蔽区的材料是纯吸收体;在 Kobayash-1-ii 中,源区和屏蔽区的材料设定为50%的散射截面.这种材料的总截面为0.1 cm-1,而空隙区域的总截面为10-4cm-1.对于每种截面,分别设置四个探测器位于坐标(15 cm,15 cm,15 cm),(25 cm,25 cm,25 cm),(35 cm,35 cm,35 cm)和(45 cm,45 cm,45 cm)处.MC 模拟使用107个源粒子,以确保所有探测器结果的最大统计误差保持在5%以下.

针对不同的探测器训练了8 个网络,每个网络的训练各基于1000 个MC 算例.随机抽取MC 和重要性数据的80%样本用作训练网络的训练集,10%样本作为用于优化网络参数的验证集,10%的样本作为最终测试训练好的网络预测效果的测试集合,按照(9)式分别计算训练样本、验证样本、测试样本与真值的偏差作为训练偏差、验证偏差、测试偏差如表3 所列,测试偏差的分布如表4 和图6 所示,由表3 和表4 可知所有情况的测试偏差均值均低于5%,小于5%的样本占总测试样本量的比例均超过90%,本数值实验中的神经网络输入是相空间内给定能量、位置、方向六维坐标的单个离散点,对应到传统MC 模拟中的单个样本,而本方法利用神经网络进行目标物理量的统计为抽样所得源粒子对目标量贡献的均值,因此预测均值偏差低于5%可以说明网络给出的结果精度符合要求.偏差分布中最大偏差结果出现在源项距离探测器最远的位置,分析原因是该位置的训练数据本身统计误差较大,使得训练得到的网络对该位置单个点源给出的偏差较大,这一特点与传统MC 单个样本模拟结果的特点相同.此外,与原始MC 模拟相比,获得这些结果所需的时间几乎可以忽略不计,用时从大约5 min 缩短到不到1 s,说明神经网络对输运计算效率的提升效果显著.作为参考,Igor 等[47]使用离散纵标法在不同硬件平台下计算完整Kobayashi 基准题的时间花费在数小时量级.

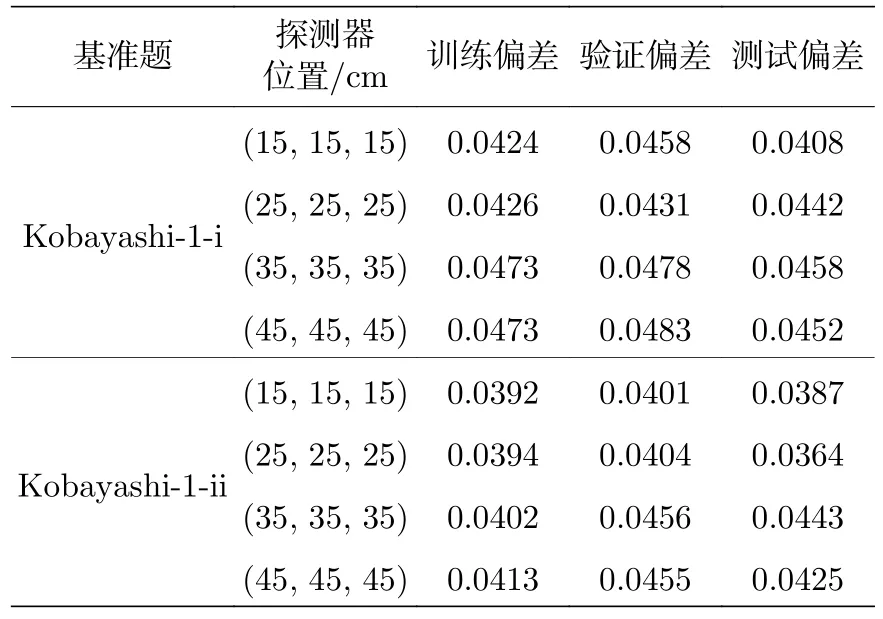
表3 Kobayashi 模型不同探测器的网络预测结果Table 3.Prediction results for different detectors by networks of Kobayashi-1.

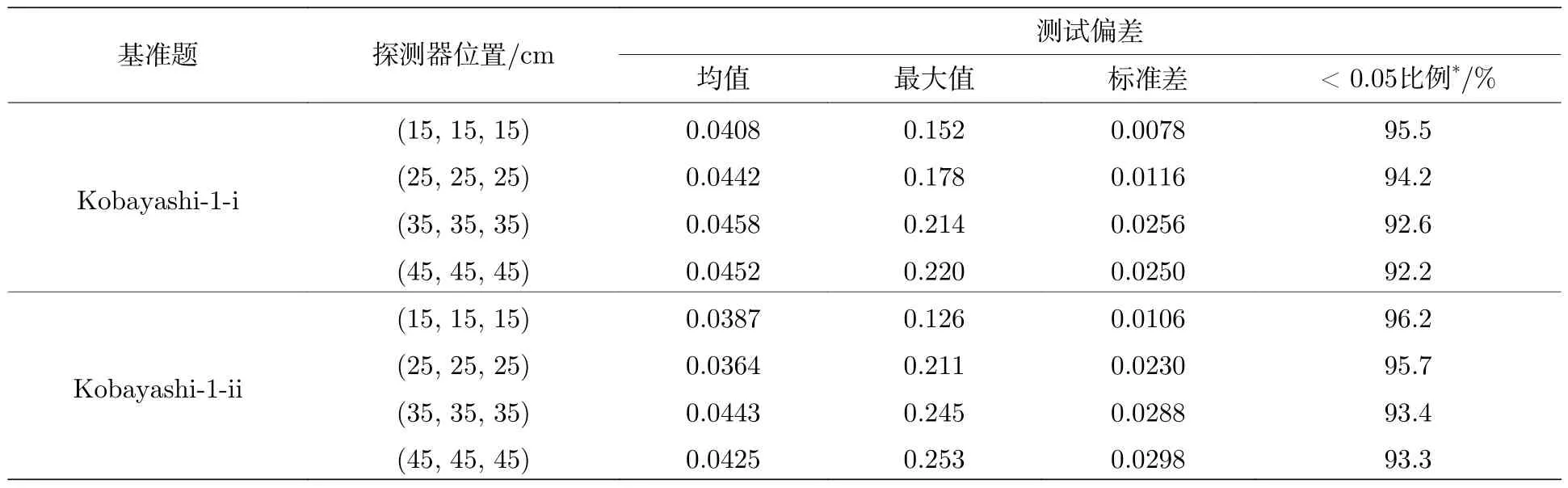
表4 Kobayashi-1 模型不同探测器的网络预测偏差分布Table 4.Deviation distributions of predicted-results for different detectors by networks of Kobayashi-1.

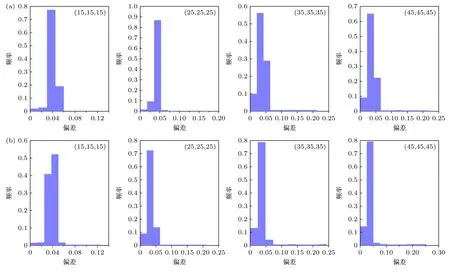
图6 Kobayashi-1 模型不同探测器的网络预测偏差分布Fig.6.Deviation distributions of predicted-results for different detectors by networks of Kobayashi-1.

3.2.3 HBR2 反应堆基准题

H.B.Robinson-2 (HBR-2)核电站是Westinghouse 公司设计的商用压水式轻水反应堆,于1971 年开始运行,归Carolina Power and Light Company 所有.H.B.Robinson-2 压力容器测定基准题[48]主要测量 HBR2 核电站压力容器内部和外部的中子通量.

HBR-2 反应堆堆芯包含157 个燃料组件、堆芯外包壳、堆芯吊篮、隔热罩、压力容器和生物屏蔽等部件.在本研究中,在OpenMC 中构建了HBR-2 反应堆结构.统计以下两个探测器(①和②)的通量为目标统计量,图7 展示了 OpenMC 中HBR2 基准题的几何结构及探测器示意图,其中左半部分为水平面示意图,右半部分为矢状面示意图.在OpenMC 中使用六层立方体来表示源项分布,每层由157 个立方体组成.

图7 HBR-2 模型几何结构示意图Fig.7.Detector geometry diagram of HBR-2 benchmark.

几何网格尺寸设定为 10.752 mm×10.752 mm×60.960 mm.源粒子发射方向为各向同性,能谱为瓦特谱.MC 模拟中模拟的粒子数量因源与探测器之间的距离而异,在源与探测器距离较远的算例中,有必要模拟更多的粒子数量以确保获得的通量统计误差达到要求,因此每个算例都模拟了 4.0×106—6.0×108个粒子,以保证最大统计误差保持在5%以下.最终利用MC 模拟共建立了942 个算例来生成真值数据集,其中754 个算例被用作为训练样本,92 个算例被用作为验证样本,92 个算例被用作为测试样本,按照(9)式分别计算测试样本、验证样本、预测样本与真值的偏差作为训练偏差、验证偏差、测试偏差(表5).

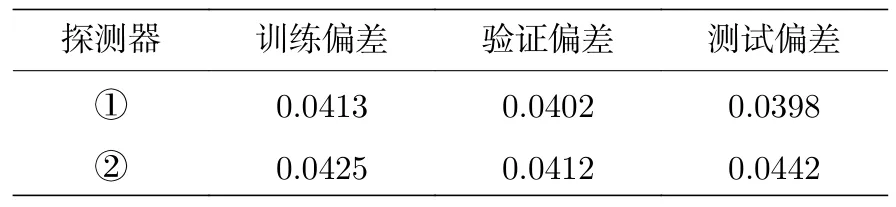
表5 HBR-2 模型不同探测器的网络预测结果Table 5.Prediction results for different location detector networks of HBR-2 benchmark.

表5 列出了网络对这两个探测器的预测结果,测试偏差的分布见表6 和图8.网络预测结果的平均相对偏差分别为3.98%和4.42%,小于5%的样本占总测试样本量的比例均超过90%,同前算例一样,最大偏差结果出现在靠近堆芯区域即源项距离探测器最远的位置,由于该位置的训练数据本身统计误差相对较大而使得单个预测结果与真值偏差超过5%.考虑到目标物理量的统计过程为从源分布中多次抽样后输入神经网络并计算对目标量贡献的均值,因此预测均值偏差低于5%表明网络输出结果精度符合要求.在时间成本方面,相对于MC模拟将计算时间从数小时缩短至约0.3 s,实现了显著提速.作为参考,Roberto[49]在不同硬件平台下使用TORT 程序基于离散纵标法对HBR-2 基准题进行计算,单CPU 时间花费在数十小时量级.可见本文提出方法可以给出满足工程精度标准的预测结果,而计算时间与原始MC 模拟相比可以忽略不计,从而获得显著的效率提升.

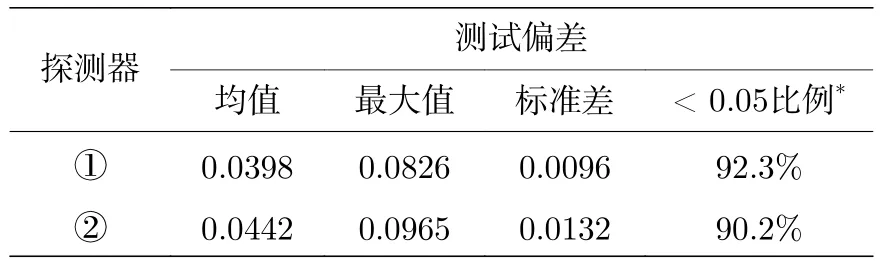
表6 HBR-2 模型不同探测器的网络预测偏差分布Table 6.Deviation distributions of predicted-results for different detectors by networks of HBR-2.

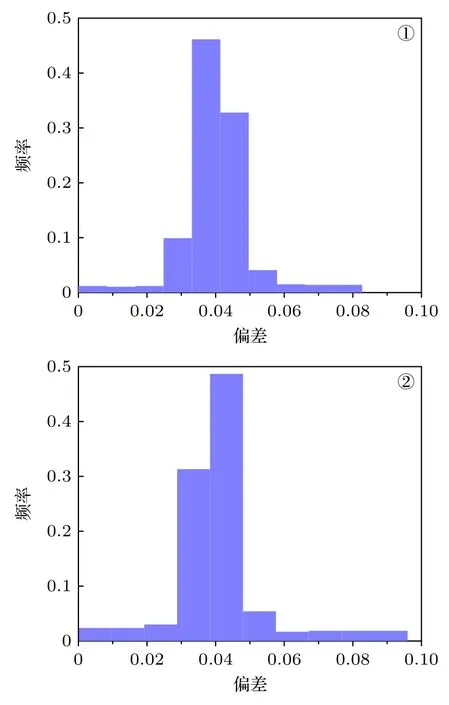
图8 HBR-2 模型不同探测器的网络预测偏差分布Fig.8.Deviation distributions of predicted-results for different detectors by networks of HBR-2.

4 结论

本文设计了用于加速中子输运问题MC 模拟的神经网络,只需一次性训练即可针对不同源项反复使用.在训练该神经网络时,使用重要性原理来高效获取足够多的高质量训练数据,从而一定程度上克服了数据生成成本高的难题.上述方法通过Kobayashi 和HBR-2 等基准问题进行了验证.网络预测结果的相对偏差始终低于5%.而且与原始MC 模拟相比,获得这些结果所需的计算时间可忽略不计.

本文研究的一个局限性是只适用于源分布有变化,而几何、材料及目标计数保持不变的情形.如果几何、材料或目标计数发生变化,则需要重新训练网络,后续研究计划将几何、材料以及目标计数的变化也作为输入信息引入网络训练过程,以增强网络的泛化能力,并以迁移学习的训练方法提高训练效率.

感谢北京应用物理与计算数学研究所勇珩研究员牵头的“ AI++”团队成员的讨论和帮助.