基于大流量止回阀实验系统的快速预测模型*
王江坤,赵 晶,3*,查洒洒,王 剑,曲洺剑,3,张俊飞
(1.沈阳工业大学 机械工程学院,辽宁 沈阳 110870;2.沈阳盛世五寰科技有限公司,辽宁 抚顺 110172;3.辽宁五寰特种材料与智能装备产业技术研究院,辽宁 沈阳 118015)
0 引 言
大流量旋启式止回阀是阀瓣绕固定轴做旋转运动的单向阀。由于具备结构简单、压降低、经济性好、密封可靠、维护维修相对方便、适用范围广等优点,大流量旋启式止回阀被广泛应用于工业生产中。
施熠徽等人[1]采用了有限元分析软件对阀门的内流场进行了分析,通过引入场协同原理,提出了2种阀结构优化设计思路,并发现了在引入协同原理对阀结构进行优化后,减小了流体的有效黏性系数平均值,增大了有效黏性系数梯度。但阀门的内流场是变化的,怎样对瞬态的流场进行优化是其需要改进的问题。
刘梦遥等人[2]采用有限元分析软件,分析了高压止回阀的应力分布及变形情况;采用流固耦合方法对止回阀进行了模拟,提出了阀口开度与止回阀变形量关联模型,发现了止回阀变形量与阀口开度呈波动趋势。但该模型只用于对阀门入口进行分析,缺失了对阀门整体的应力分布分析。余航等人[3]采用流固热耦合仿真方法,研究了温度快速变化对止回阀的影响;采用流体力学计算技术,对工况变换时止回阀的内部流场进行了仿真,提出了基于止回阀对温度场的建模方法,发现了止回阀的等效应力和变形量随温度的降低而降低;但其没有分析外界条件对止回阀的影响。竺盛才等人[4]采用有限元仿真软件,研究了接触面在工作中所受的冲击效应,采用有限元分析方法,建立了各个部件之间的接触关系和有限元分析模型,发现了切换阀速度与应力峰值产生部位分别为阀板、阀体挡台距离转轴最远处;但其对于快速响应预测没有进行研究。
大多数研究是对止回阀进行单独分析,很少有研究人员对止回阀实验平台进行系统分析。所以需要建立实验系统快速预测模型,从而快速预测整个实验系统的状态信息。
笔者利用机器学习算法建立阀门实验系统快速预测模型。首先,利用有限元软件对大流量止回阀实验系统进行建模分析,并通过比对实验数据和仿真数据,确保仿真数据的可靠性;然后,针对实验系统,利用多种机器学习算法建立快速预测模型。
1 快速预测模型技术路线
快速预测模型的技术路线分三部分:1)数据准备阶段;2)模型训练阶段;3)结果分析阶段。
快速预测模型技术路线如图1所示。
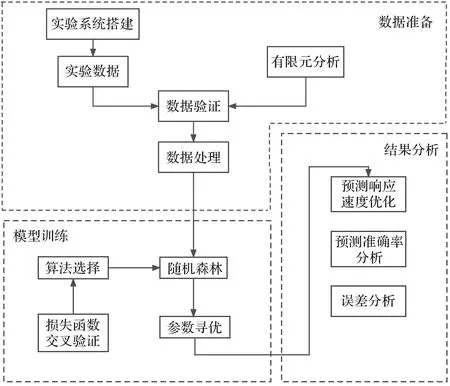
图1 快速预测模型技术路线
1)数据准备阶段。搭建实验台架,并进行实验,将实验数据与有限元仿真数据进行对比,验证数据的可靠性。通过对数据的归一化处理,消除量纲影响,形成训练数据集;
2)模型训练阶段。使用均方误差指标(mean squ-ared error, MSE)、平均绝对误差指标(mean absolute error, MAE)、R2指标对DNN、RF、GBDT[5-7]三种算法进行机器学习,选择表现最好的随机森林算法训练数据,并采用粒子群算法[8]对快速预测模型的参数进行寻优;
3)结果分析阶段。随机选择一组初始值,用训练完成的快速预测模型进行预测,观察预测的响应速度、预测准确率和误差值并进行分析优化。
2 实体模型搭建
2.1 实验台架结构
大流量止回阀实验系统由阀门、管道、流量计、压力表、循环水泵共同组成。
实验系统示意图如图2所示。
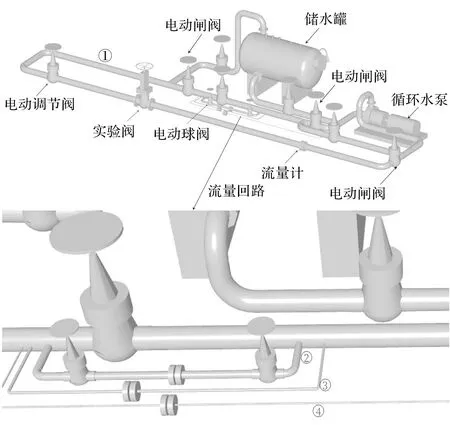
图2 实验系统示意图
由图2可知:实验系统由4条回路组成,第1条回路为主工作回路,主要测试实验阀门的应力、应变和流量。因为不同流量对应的流量计不同,2、3和4这3条流量回路用于测试不同流量下实验阀门的应力、应变。
在进行有限元分析时,3条流量回路可以通过有限元软件的参数设置进行代替,不需要3条流量回路的辅助,所以可以将3条流量回路进行简化,只留下主回路部分并进行有限元分析。同时,对于储水罐和循环水泵的泵机部分一并进行简化,用参数代替。
2.2 有限元参数设置
实验台架以AISI 321不锈钢为材料,其弹性模量为193 GPa,泊松比为0.28,密度为7 900 kg/m3,屈服极限为205 MPa。
笔者选择通用性较强的四面体网格,网格最小尺寸单元尺寸100 mm,节点数为663 693。
2.3 数据验证
为了验证仿真数据的可靠性,笔者选取实验系统的关键点位与仿真数据进行对比,选取容易发生应力集中的点位作为实验系统的关键点位。
实验阀门应力如图3所示。

图3 实验阀门应力
由图3可知:应力较大的点主要在阀门颈部、阀门管道连接处。因此,笔者选择这些点位作为关键点位。由于实验数据会受到噪声的影响,所以在进行数据验证之前,需要先对实验数据进行异常值清洗。笔者采用3sigma原则将实验数据进行处理,然后将其与仿真数据进行对比分析。
应变数据对比如表1所示。
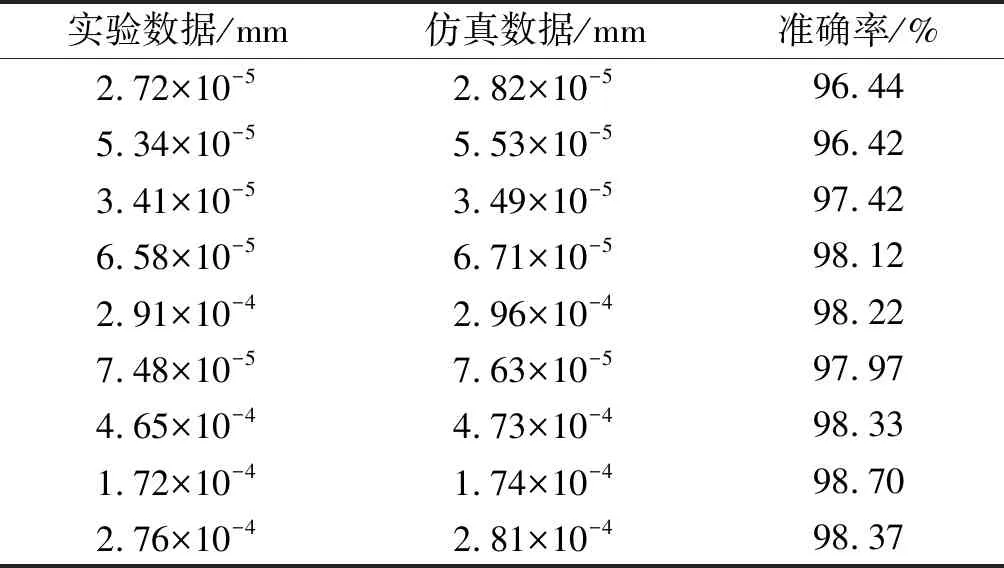
表1 应变数据对比
由表1可知:仿真数据的准确率最小值为96.42%,说明仿真数据满足误差要求,可以代替实验数据构建训练集。
2.4 数据处理
由于大流量止回阀实验系统应变数据区间为10-4~10-5,而应力的数据区间为0~100,因此笔者采用最大最小值归一化法,消除应力应变的量纲差异。
对于应力应变的原始值y1、y2,具体表示如下:
y1_scaled=(y1-min)/(max-min)
(1)
y2_scaled=(y2-min)/(max-min)
(2)
式中:y1_scaled为归一化后的输出应力;y2_scaled为归一化后的输出。
笔者通过将原始值与最小值的差异除以最大值和最小值之间的范围来进行归一化,最小值会被映射到0,最大值会被映射到1,对于其他值,则在这个范围内线性地进行缩放。
关键点位归一化数据如表2所示。

表2 关键点位归一化数据
由表2可知:归一化后的数据消除了量纲的影响,应力、应变的数值范围相近,解决了因数值差距过大而导致某些特征对模型训练贡献值小的问题。
3 快速预测模型关键技术
快速预测模型是指用机器学习的方法进行大量数据训练,训练出响应速度快、预测准确率高的模型。快速预测模型技术针对给定的任意初始条件,能够快速预测整个实验系统的应力、应变变化。
3.1 算法选择
DNN[9-12]在大数据机器学习中具有高度可扩展性和强大的表征学习能力,能够处理大规模数据集和模型参数,通常具有较高的准确性。然而,训练和调整DNN模型复杂且耗时,对小数据集容易过拟合,且对特征工程依赖较高。
随机森林能够并行处理大规模数据,具有良好的鲁棒性,能够处理异常值和噪声,可以进行特征选择,降低计算和存储成本。但随机森林可能占用较大内存空间。
GBDT[13]具有高准确性和可解释性等特点,适用于高维稀疏数据,能够处理大量特征变量。然而,GBDT训练和预测速度较慢,对噪声和异常值敏感,处理大数据集和高维数据时需要更多计算资源。
随机森林算法[14-15]构建的预测模型在实验系统的样本训练数据下,其均方误差指标(root MSE)、平均绝对误差指标(root MAE)、R2都明显优于DNN模型以及GBDT模型。
应变损失值如表3所示。

表3 应变损失值
由表3可知,采用DNN和GBDT算法构建的模型有较低的均方误差和平均相对误差,结合归一化后的数据值,这两种算法应该有较好的拟合曲线[16-17]。但通过R2值可以发现,两种算法的拟合效果并不好,说明这两种算法构建的模型发生了过拟合。
因此,在对比了RMSE、RMAE、R2三种指标后,笔者选择使用随机森林算法构建快速预测模型。
随机森林的构建预测模型过程可以简述为:对整个训练集进行Bootstrap重采样,生成新的训练集。
抽取n个样本形成子集,每个子集对应一棵决策树,重复m次,就构建了具有m棵决策树的随机森林快速预测模型。
随机森林构建预测模型原理如图4所示。
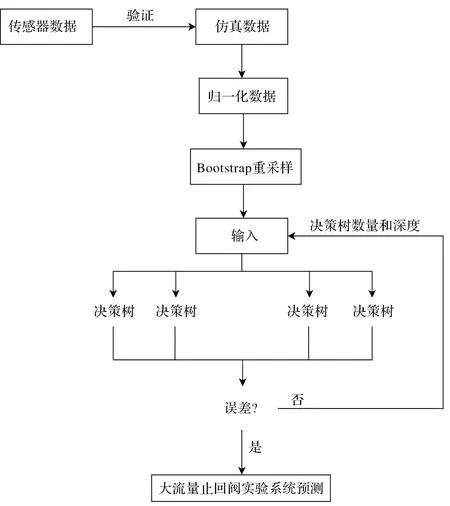
图4 随机森林构建预测模型原理图
随机森林算法的计算过程如下:
1)通过bootstrap重采样,将样本打乱,从抽取的样本集中选择合适的样本,组成n个子集,每个子集对应一个决策树训练集;
2)子集中包含M个特征,随机抽取m个特征的子集Ki。根据信息增益最大化的规则选择决策树分支结点,具体表示如下:
(3)
式中:Gain(Ki,a)为特征a对子集Ki属性划分获得的信息增益;Ent(Ki)为子集Ki信息熵。
3)遍历子集Ki各项特征数据,将找到的信息增益最大化的特征a作为决策树分支结点,并将节点分裂为两个分支,通过决策树持续分支生长而不进行剪枝,使所有特征都完成分裂过程;
4)利用决策树对特征集实施类别投票,根据投票结果,将得票数较多的类别作为诊断类型。
3.2 随机森林参数确定
粒子群算法[18-21]是一种兼顾全局和局部最优的随机搜索算法。所以,需要利用粒子群算法寻找随机森林模型的最优参数。
笔者以群体最优值为基准,对每个粒子的位置x与速度v进行更新,更新公式为:
位置x更新公式为:
xi(k+1)=xi(k)+vi(k+1)
(4)
式中:xi,vi为粒子的位置与速度。
速度v更新公式为:
vi(k+1)=wvi(k)+a1r1(pbi(k)-xi(k))+a2r2(gbi(k)-xi(k))
(5)
式中:w为惯性因子;a1,a2为学习因子;r1,r2为(0,1)之间的随机数。
笔者以损失函数为目标函数进行寻优,最终的搜索结果表明,决策树的最优棵数为50棵,对应的预测准确率达到97.56%。
4 快速预测模型结果分析
笔者利用随机森林算法建立大流量止回阀实验系统快速预测模型,并对所得实验系统应力应变预测数据进行反归一化;同时,将样本节点映射至原始实验系统节点中,得到实验系统对应的预测数据。
4.1 响应速度与预测准确率分析
快速预测模型的响应速度是一个很重要的评价指标。模型的响应速度与模型的复杂程度成反比,而模型的复杂程度又与模型的预测准确率成正比。因此,模型的响应速度与模型的预测准确率成反比,所以,笔者针对两者相互影响情况进行实验验证。
实验系统响应时间如表4所示。

表4 实验系统响应时间表
由表4可知:随着决策树数量增加,预测模型响应时间和预测准确率都在增大;当决策树数量从25增长到30时,预测模型响应时间提高2倍,预测准确率只增加了0.03%。
由此可知:当决策树数量到达25棵以后,预测准确率提升所需要的成本太高。所以,笔者选取决策树数量为25棵为预测模型的最优参数。
4.2 误差分析
笔者随机选取一组有限元分析结果进行预测,采用实验系统快速预测模型所得应力应变预测结果和有限元分析结果吻合。结合评价模型和预测曲线得出结论:在大流量止回阀实验系统的应用场景下,采用随机森林算法能够实现多目标同时准确输出目的,适合实验系统运行状态下的快速预测。
应变和应力预测结果如图5所示。

图5 应变应力预测图
由图5可知:误差值在前后两部分发生跳动,这是因为阀门数据与管道数据一起训练,阀门应力应变的变化比管道复杂,所以会导致阀门部分误差比管道部分大。阀门部分单独建模,可以减小误差曲线的跳动。
实验阀门响应时间如表5所示。
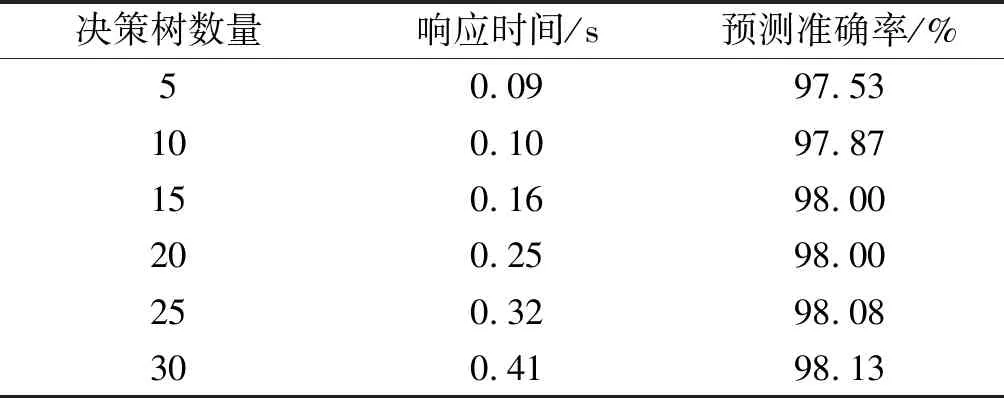
表5 实验阀门响应时间
由表5可得到在决策树数量为25时,实验阀门快速预测模型的响应速度。
结果表明:模型的响应时间为0.32 s,实验系统整体快速预测模型的响应时间为0.53 s。实验阀门的数据量只有实验系统数据量的1/6,说明采用阀门部件单独构建快速预测模型,将大幅增加预测模型的响应时间。同时,实验系统整体快速预测模型的误差满足预期误差。
因此,笔者采用实验系统整体快速预测模型。
4.3 实验验证
实验数据与预测模型之间存在双向反馈机制。实验系统在前文提到的关键点位放置应力和应变传感器,采集实验数据对预测模型的预测值进行实时验证。采用预测模型能发现实验系统的应力和应变异常点,并发出警告。
实验系统实验与仿真数据对比如表6所示。
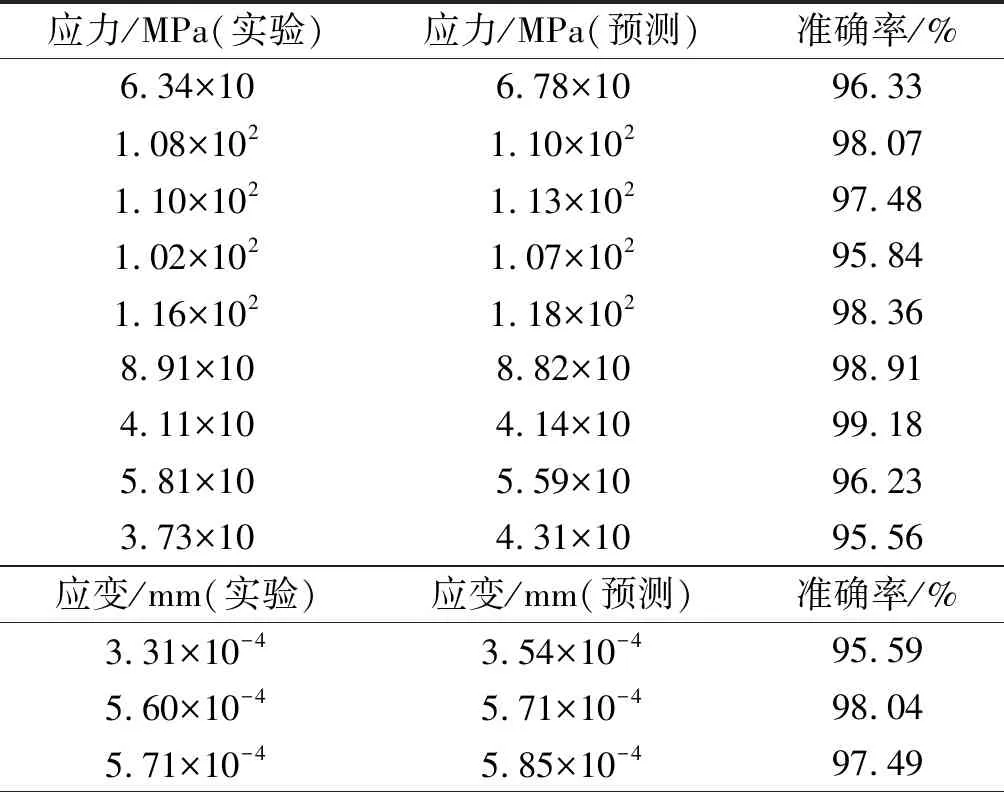
表6 实验系统实验与仿真数据对比
由表6可知,在内压为1.9 MPa时,实验数据与预测数据对比的准确率均在95%以上,可以满足预期误差要求。
5 结束语
针对传感器对于数据获取的局限性,笔者对大流量止回阀实验系统的快速预测模型技术进行了研究。
笔者通过搭建实体模型,并利用快速预测模型的关键技术,构建了实验系统数据库,完成了实验系统的样本采集;然后,通过比对不同机器学习算法的预测准确率,选择利用随机森林算法,建立了实验系统的快速预测模型;最后,进行了快速预测模型的结果分析。
研究结论如下:
1)基于应力应变样本数据库中的数据,利用随机森林算法建立大流量止回阀快速预测模型,拟合优度R2达到0.99;
2)随机抽取一组样本作为测试集,预测准确率达到97.43%,同时模型响应时间为0.53 s,验证了快速预测模型的可靠性,这对于大流量止回阀实验系统分析具有重要参考价值;
3)对比了整体预测模型和部件单独预测模型的预测速度和精度。部件单独预测模型的预测精度比整体预测模型高1%,但预测速度是整体预测模型的30%。
模型的预测精度还有提升空间,如何在不影响预测模型响应速度的前提下提升模型的预测精度,这是笔者接下来的研究重点。

