风电齿轮箱迷宫密封泄漏量分析及结构优化设计*
高羡明,张 洋,张功学,杨汶轩,蔡志祥
(陕西科技大学 机电工程学院,陕西 西安 710021)
0 引 言
迷宫密封的主要作用是控制密封结构间隙中流体从高压侧向低压侧流动产生的泄漏,从而减小润滑液泄漏的损失成本,提高透平机械的密封性能。在实际工况中,接触面的接触振动和液体旋转过程中产生的热量可能导致迷宫密封的接触面发生碰触,从而使密封齿发生断裂和磨损,引起其在迷宫密封出口处出现泄漏现象[1]。
目前,针对迷宫密封严密性能的研究主要集中在其结构参数。随着透平机械逐渐向高转速、高效率的方向发展,由迷宫密封接触面碰撞导致的密封齿磨损和密封性能减退的问题越来越严重。
WHALEN J K等人[2]系统研究了常见的几种金属迷宫密封在碰磨过程中的几何变形,得到了迷宫密封在工作过程中摩擦的变形规律和对泄漏量的影响。DOGU Y等人[3]研究了密封齿和转子面上不同类型的磨损对迷宫密封泄漏特性的影响,得出了泄露量在不同种类迷宫密封工作过程的变化规律。YUCEL U等人[4]通过数值模拟和实验两种方法研究了温度、压差、空腔数目和齿形等因素对迷宫密封性能的影响,得出了泄漏量随几何参数和动力学参数的变化规律。EI-GAMAL H A等人[5]在转轴旋转和静止的两种情况下,通过改变迷宫密封内部腔体的尺寸来研究其密封性能,得出结果表明,随着腔体深度的增加,泄漏量表现得越来越弱,且腔体深度有一个临界值使得密封性能最好。巴鹏等人[6]以往复式压缩机为研究对象,对往复式压缩机的泄漏量进行了数值模拟,通过对比复式压缩机不同结构的特点与流体的流动特征,分析了在不同的密封结构下的密封性能,得到了往复式压缩机流体在密封腔的流动特征,对其结构的性能与参数进行了优化。丁军等人[7]以高温的条件下气冷堆主氦风机级间的迷宫密封为研究对象,采用数值模拟和搭建密封试验台的方法,研究了迷宫密封中泄漏量的大小与出入口压力差、旋转轴的转速和密封腔的宽度等动力学参数与结构尺寸的关系。衣可心等人[8]为探讨小密封间隙下离心制冷压缩机性能变化规律,利用计算流体动力学(computational fluid dynamics,CFD)方法,揭示了迷宫密封流体的压力由进口到出口依次降低和泄漏量与密封间隙的关系,有效降低了泄漏量。马文生等人[9]研究了转子系统在迷宫密封中的作用,建立了其动力学模型,并分析了迷宫密封的动力学参数,根据数值模拟的方法,得到了泄漏量与迷宫密封结构尺寸之间的数值关系,得出研究结论,在一定范围内增加迷宫密封的密封间隙的大小会使泄漏量有更好的稳定性;但是持续增加密封间隙则会造成泄漏量稳定性地下降,因此在此范围内会存在一个临界值,此时的密封间隙对应最小的泄漏量。
尽管这些学者在迷宫密封方面取得了部分研究成果,但对其进行结构参数优化设计的研究几乎未见触及。
笔者利用数值模拟方法,研究进出口压力比、润滑液动力黏度、高速轴与低速轴的转速和迷宫密封的密封齿间隙对某风电齿轮箱迷宫密封泄漏量的影响机制;通过多参数集成构建代理模型,通过风电齿轮箱迷宫密封结构参数对泄漏量的影响,获得最优结构参数,探究影响迷宫密封泄漏量的因素。
1 实体模型的建立
迷宫密封结构的设计是为了在其内部流体容易向外部泄漏的区域上设计几个齿或槽形结构,这些结构能够在流体通过密封间隙时施加阻力,有效节流,消耗在腔体内的能量,减弱其泄漏量[10]。
在上下接触的轴上加工若干个上述两种结构,轴上径向接触区域会因为这些结构的存在形成若干个小的空隙;轴向方向就形成若干个腔体,两个接触的轴上两种结构的分布排列形成了完整的迷宫密封通道,从而达到密封的效果。这样的通道会使得内部流体产生漩涡,从而达到在最后一级密封时将压力减小到与外界压力相同,避免泄漏现象的出现。
笔者为某风电齿轮箱端盖部分设计了迷宫密封结构。
齿轮箱三维模型如图1所示。

图1 风电齿轮箱三维模型
笔者以某风电齿轮密封箱为例,建立迷宫密封流体的三维模型。由于完整的迷宫模型较大,为了减少迭代计算时间,提高计算效率,笔者将端盖处的迷宫密封三维模型简化。
迷宫密封截面图如图2所示。
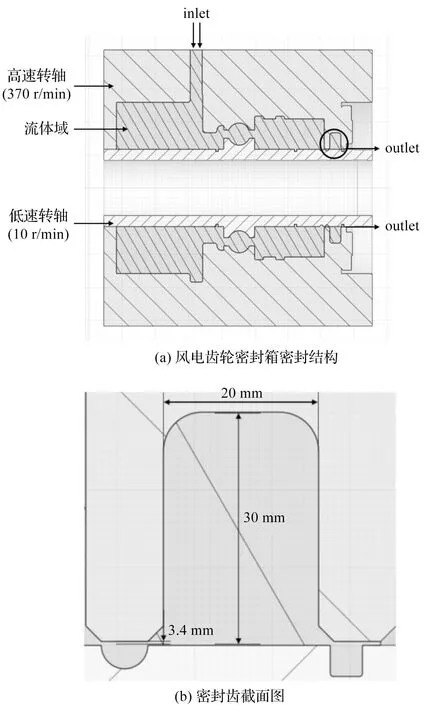
图2 风电齿轮密封箱密封结构及密封齿截面图
迷宫密封包含流体区域、两个转速不同的转轴以及流体进出口,其中密封齿的截面图具体参数如上图。
风电齿轮箱流场模型各部分结构的具体几何参数值和数值模拟边界条件的参数值,如表1所示。

表1 迷宫密封的几何尺寸、数值模拟的边界条件
2 计算机流体动力学(CFD)模型
2.1 控制方程
1)湍流控制方程
湍流流动模型是三维的、非稳态的流动,并由速度、压力和温度等尺度组成,在数值计算中采用湍流模型来模拟湍流的状态,即以脉动运动方程和雷诺平均运动方程为基础[11]12。
k-ε模型是一种基本的双方程湍流模型,k表示湍流动能,是速度波动的方差;ε表示湍流涡旋耗散。k-ε模型的模拟效果较佳,应用较广泛。
数值模拟选用标准k-ε模型,k-ε的表达式为:
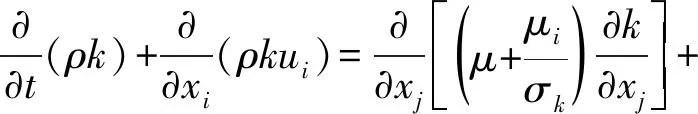
(1)
(2)
湍流黏度系数为:
(3)
速度引起的湍动能为:
(4)
2)守恒方程
流体在迷宫密封中的流动要满足湍流方程、动量守恒方程和能量守恒方程[11]13,其守恒方程的通用形式为:
(5)
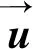
2.2 网格划分与结果分析
选取合适的网格类型及合理的网格划分方法是仿真成功的关键,网格形式对计算精度及计算量有密切关系。在网格划分时会出现网格变形过大而计算不准确或不收敛的现象,这是在四面体网格转换为六面体网格过程中造成的。为了保证迷宫密封流体区计算的准确性,初始的边界条件为:进口压力为0.2 MPa、出口压力为一个大气压、密封间隙为3.4 mm;选取网格数量为8.80×105、9.80×105、1.10×106、1.20×106和1.30×106的五种网格,以迷宫密封的泄漏量为输出指标,进行网格无关性验证。
由迷密封泄漏量与网格数量的关系可知,当网格数量从1.10×106增加到1.30×106时,密封泄漏量从0.005 8 kg/s增加到0.005 9 kg/s,在可控范围之内,可以视为网格无关,划分网格的数量保持在1.10×106以上,确保计算的准确。
网格无关性验证如图3所示。

图3 迷密封泄漏量与网格数量的关系
网格划分完成,该迷宫密封流体结构网格划分后的单元数量为698 587,网格节点数为1 119 258,所以在保证最终计算结果快速并且无明显差别的前提下选用四面体网格。
网格划分示意图如图4所示。

图4 迷宫密封内部流道网格数量划分示意图
笔者利用Fluent软件对上述网格划分后的模型进行了数值模拟,计算出其泄漏量为0.005 821 kg/s;同时,采用Vermes、Kearton、Egli、迭代计算法这几种理论计算方法进行了计算[11]29。Vermes计算方法有完善的模型,计算结果在上述五种方法中最为精确,但是计算过程在五种方法中最为复杂,以Vermes法所计算的泄漏量为参考,数值计算法与其相比误差在5%以内,并且数值模拟计算方法简便。
故笔者采用数值计算法对迷宫密封进行分析,其误差如表2所示。
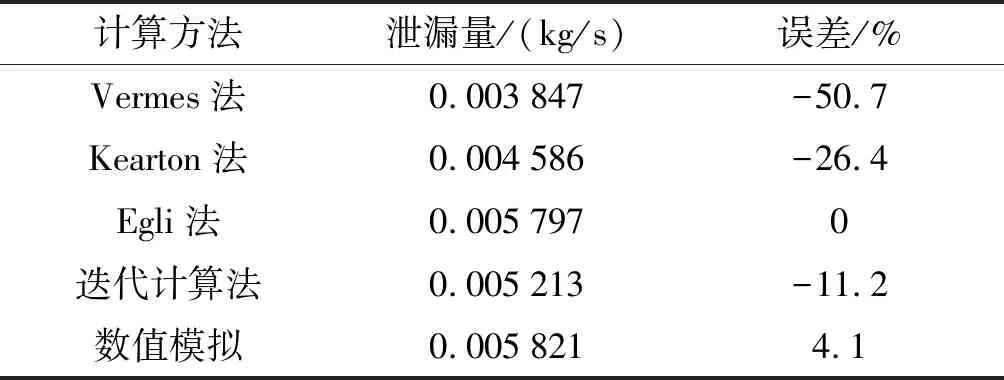
表2 理论计算和数值模拟误差分析
网格划分完成后,笔者根据风电齿轮箱迷宫密封内部流体的实际情况,在其仿真时,将初始化参数做如下假设[12-14]:
1)流场的介质为液体。除分析润滑液动力黏度影响外,其他计算时选择水为工作介质;
2)壁面的边界条件设置为绝热壁面;
3)由于模型结构有很好的对称性,在进行仿真时忽略转子的径向和轴向偏移。
3 仿真结果分析与数值模拟
3.1 速度场矢量图分布
根据迷宫密封内部流场的速度矢量图,密封腔内形成回流是因为流体以环形的方式在空腔中分布,流体速度最大的地方在迷宫密封入口附近的壁面上。
流体矢量图如图5所示。

图5 迷宫密封流场速度矢量图
在几个空腔内形成的漩涡会使流体回流,抑制其进入下一个空腔,在几个空腔内部循环流动。流体在经过迷宫密封最后一个空腔的位置时,在其内部会有一个低于大气压的现象出现,阻止其在出口处溢出。此时出口处的最大速度为5.87 m/s。
3.2 压比、转速与泄漏量关系
笔者通过进出口压力比和高速轴与低速轴转速的变化对泄漏量的影响进行验证。
在不同进出口压力比下,高速转轴6种转速条件的泄漏量如表3所示。
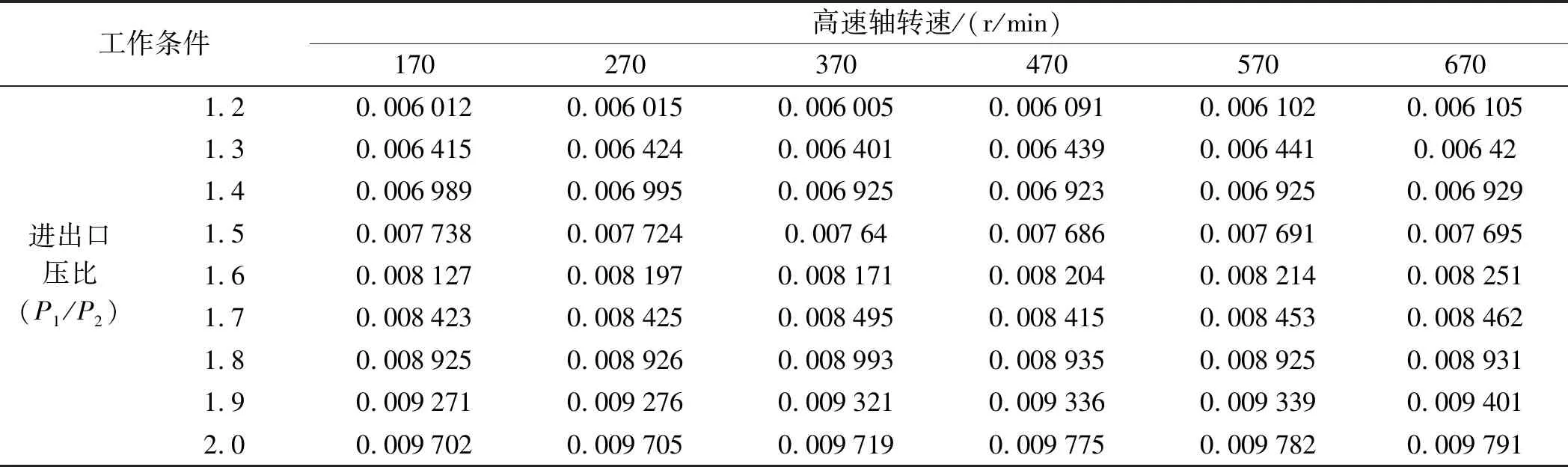
表3 不同高速轴转速和进出口压比的泄漏量
由表3可知:在只改变进出口压力比和高速轴、低速轴的转速,出口压力保持为一个大气压的条件下,使进出口压比(P1/P2)在1.2~2.0范围内,高速轴转速的转速分别为170 r/min、270 r/min、370 r/min、470 r/min、570 r/min、670 r/min,低速轴的转速分别为10 r/min、20 r/min、30 r/min、40 r/min、50 r/min、60 r/min,进行数值模拟,并计算出所对应的泄漏量。
高速轴转速和压比对泄漏量的变化示意图如图6所示。

图6 不同高速轴转速和压比对泄漏量的变化曲线
由图6可知:泄漏量受进出口压力比的影响更大,且与泄漏量呈正比,高速轴6种转速下的泄漏量变化曲线位置大致相同,即泄漏量受齿轮箱高速轴转速影响较小。所以应选择较小的进出口压力比使得泄漏量最小,选择较小转速时,齿轮箱在工作时更加稳定。
笔者分别列出了在不同进出口压力比下低转轴6种转速条件下泄漏量的大小。
不同低速轴转速和进出口压比下泄漏量具体参数如表4所示。
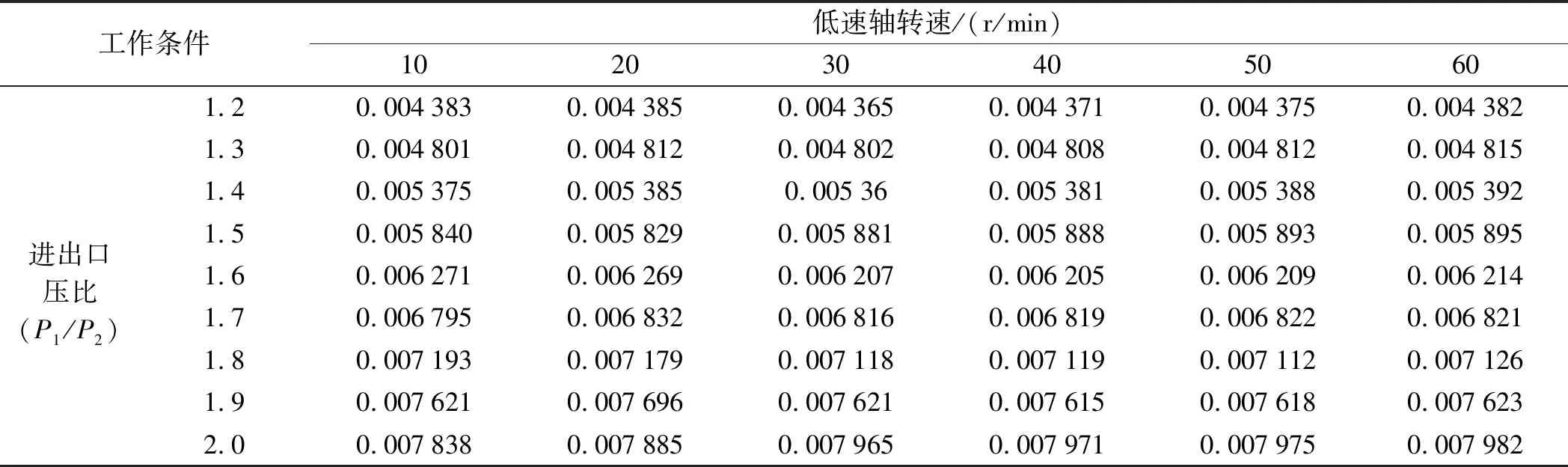
表4 不同低速轴转速和进出口压比的泄漏量
由表4可知:泄漏量的影响与高速轴的结果一致,在不同低速轴转速下,低速轴的转速对泄漏量的大小影响不大。
根据6种转速下泄漏量的大小,考虑工作环境以及使用的经济性来选择低速轴转速,所以应选择较小的进出口压力比使得泄漏量最小,低速轴转速较小时,齿轮箱在工作时更加稳定。
不同低速轴转速和压比对泄漏量的变化曲线如图7所示。

图7 不同低速轴转速和压比对泄漏量的变化曲线
对比两个转轴不同转速下泄漏量的大小可知,不论是高速轴还是低速轴的转速都对泄漏量的大小影响不大。
笔者在选取该齿轮箱转轴实际转速时,最高只考虑到670 r/min,所以对超高转速(转速大于1 000 r/min)的转轴,此结论不一定适用,需另作考虑。
3.3 润滑液黏度、温度与泄漏量关系
随着转轴的转动,齿轮箱箱体内润滑液的温度会不断升高。笔者在考虑温度升高对润滑液动力黏度影响的同时,将温度的变化情况与润滑油黏度的变化情况结合起来,分析润滑油黏度和温度的变化是否对迷宫密封的泄漏量有影响,利用数值模拟的方法进行了分析验证,选择5种牌号的润滑油[15]进行了分析。
润滑油动力黏度如表5所示。
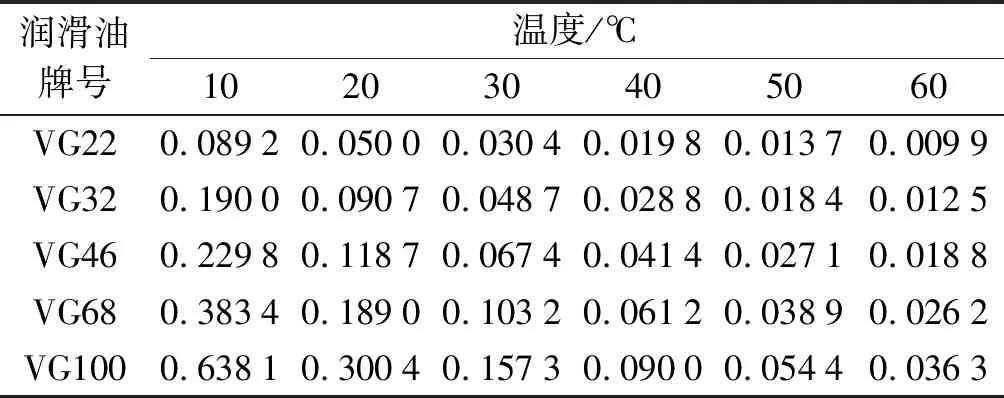
表5 不同温度下不同牌号润滑油的动力黏度
笔者计算出不同温度和不同牌号的润滑油的泄漏量,得知润滑液的动力黏度与温度成反比,当工况温度在10 ℃~60 ℃的范围内变化,所选择的5种润滑油动力黏度随牌号依次增大(VG22~VG100)。
不同润滑油黏度和温度范围内计算出的泄漏量如表6所示。
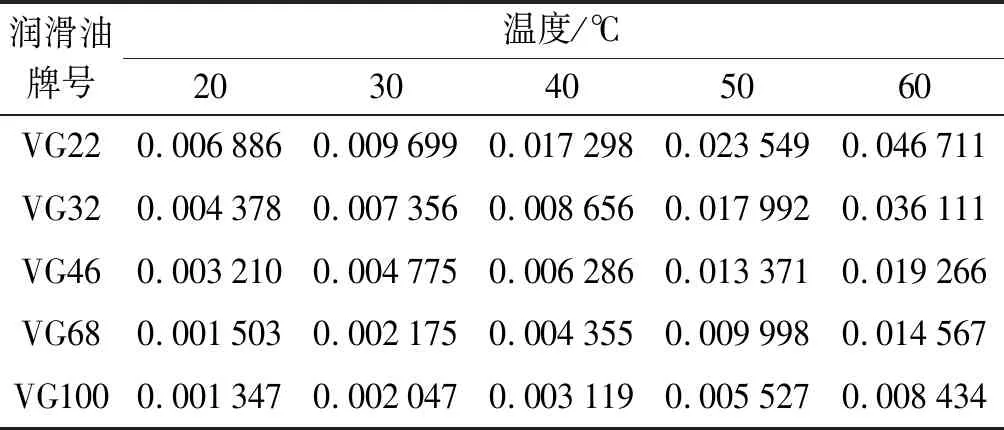
表6 不同润滑油牌号和温度的泄漏量
由表6可知:不同润滑油牌号下泄漏量随温度变化的总体趋势大致相同,但是随着温度的升高,润滑油牌号越高对泄漏量的影响则越小。结果表明,温度对润滑油的动力黏度有显著影响;工作时,温度对泄漏量也会产生影响,即齿轮箱在工作时,应避免温度过高的现象出现;应选择润滑油动力黏度值较大的使用,即选择较低的温度和较大牌号的润滑油。
润滑油黏度和温度对泄漏量的影响变化曲线如图8所示。
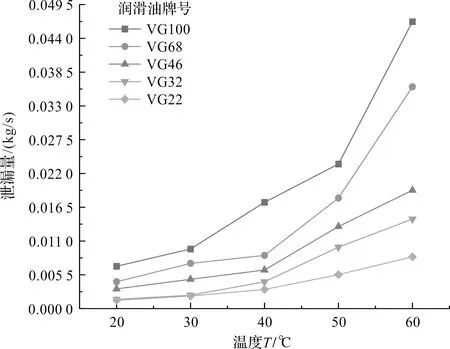
图8 润滑油黏度和温度对泄漏量的变化曲线
从图8可以看出:工况温度升高的同时减小润滑油牌号,会导致润滑油的动力黏度随之减小,而迷宫密封的泄漏量会随之增大。
3.4 迷宫间隙与泄漏量关系
迷宫密封的密封间隙是对其内部流体的密封阻隔非常重要的结构,密封间隙很大时,无法起到对内部流体密封阻隔的作用,泄漏量随着间隙的增加而增大;密封间隙很小时,可以提高其密封性能,此时对迷宫密封材料的设计、性能、制造加工工艺和装配过程都有着更高的要求。笔者对迷宫密封间隙在3.4 mm至4.0 mm范围内进行数值模拟。
迷宫密封间隙对泄漏量大小的影响如表7所示。
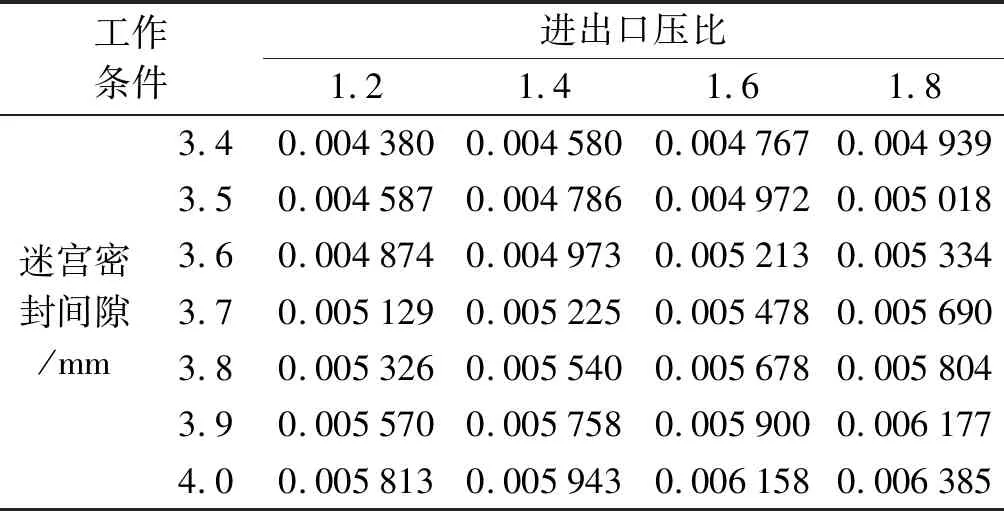
表7 不同间隙和压比的泄漏量
当进出口压力比固定不变,密封间隙不断增大时,会导致泄漏量不断增大,不同进出口压比下泄露量随迷宫密封的变化如图9所示。

图9 不同的压比和密封间隙下对泄漏量的变化曲线
由表7和图9可知:在不同的进出口压力比和相同的密封间隙下,泄漏量的变化趋势大致相同,进出口压力比对泄漏量的影响不大;而迷宫密封间隙大小与泄漏量成正比。
所以,在满足加工难度和安装条件方便的前提下,应选用密封间隙较小的值,从而保证迷宫密封的密封性能。
4 基于RBF代理模型的参数优化设计
4.1 设计变量与输出参数的设计
笔者在影响风电齿轮箱中迷宫密封性能的因素中,选取密封间隙x1、密封腔体高度x2和密封腔体高度x3三个结构参数作为设计变量,以迷宫密封的泄漏量f1和密封出口处的最大速度f2,取最小值为目标进行优化设计。
此时,初始泄漏量f1为0.004 836 kg/s、密封出口处的最大速度f2为5.87 m/s。
设计标量的取值范围如表8所示。

表8 设计变量及其取值范围
考虑迷宫密封的实际结构尺寸,选取设计变量的取值范围,搭建代理模型之前,首先需要获得所需样本点。为了兼顾运算时间和代理模型的精度,笔者采用最优拉丁超立方法获取30个样本点[16],进行实验设计。
样本数据仿真分析结果如表9所示。

表9 样本数据仿真分析结果
笔者将获取的样本点输入到仿真模型中计算,求解出相应的目标函数值。
4.2 代理模型的建立与精度评估
目前常用的构建代理模型的方法有响应面模型、克里格模型、径向基神经网络模型和正交多项式模型[17]。
在迷宫密封泄漏分析计算过程中,设计变量和输出响应之间具有很高的非线性,而径向基神经网络模型在拟合非线性程度较高的函数关系时,具有很强的鲁棒性。
设计变量和输出变量的部分响应面如图10所示。

图10 设计变量和输出变量部分响应面
根据图10设计变量和输出变量的部分响应面关系图,笔者选用径向基神经网络模型法建立代理模型[18],基于30组样本数据分析结果,建立迷宫密封的代理模型,探求设计的三个变量与两个输出变量之间数量关系。
输出变量f1、f2各误差值判定结果如表10所示。

表10 误差判定结果
由表10可知:各目标函数的均方根误差不超过0.04,且确定性系数均大于0.97,这说明所建立的代理模型具有较高的精度,可替代仿真模型做进一步优化设计。
为了评估所建立代理模型的准确性,笔者随机抽取样本空间10组样本点进行误差分析。
各目标函数的误差分析如图11所示。
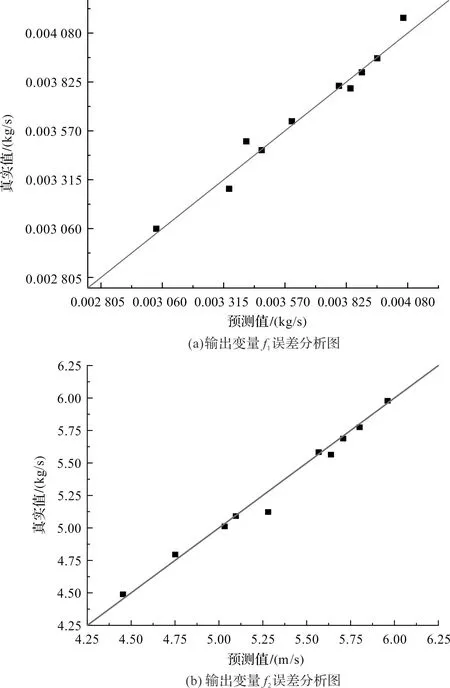
图11 输出变量误差分析图
由图11可知:10组样本点所建立的响应面模型可以很好地拟合输入与输出变量之间的关系,误差结果在可接受范围之内。
在统计学中,有4种误差分析的评价指标[19-23],这4个指标可接受的范围为:平均误差低于0.2、均方根误差低于0.2、最大绝对值误差低于0.3、确定性系数不低于0.9。
4.3 基于代理模型的多目标优化
笔者所建立的迷宫密封结构的优化数学模型如下式所示:
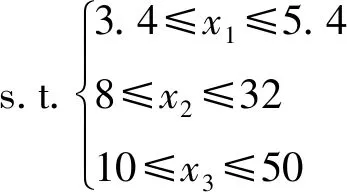
(6)
基于构建的径向基神经网络代理模型,笔者采用NSGA-Ⅱ算法对多目标优化模型进行求解。
种群个数为100,迭代次数为50,交叉概率为0.9,泄漏量和出口最大速度的优化进程,如图12所示。
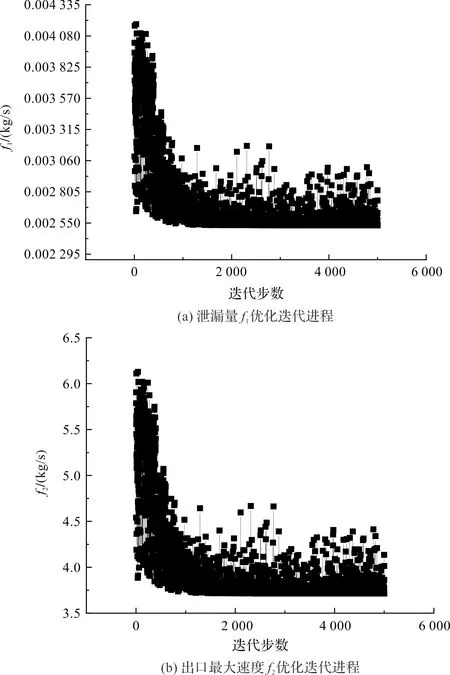
图12 输出参数优化进程示意图
由图12可知:对输出参数设置完成后,运行进行5 000步优化迭代,优化仿真模型得到了ISIGHT参数优化结果;根据输出参数优化得到最优解,并将其代入相对应的迷宫密封参数,进行数值模拟。
笔者得到最优参数组并保留一位小数:x1=1.5 mm,x2=15.8 mm,x3=26.3 mm,并将所得优化后的参数输入仿真模型中进行仿真分析。
在相同输入条件下得到的目标函数误差值如表11所示。

表11 优化结果验证
由表11可知:基于代理模型的优化结果与将优化参数输入仿真模型得到的结果,代理模型理论值与有限元数值模拟误差值不超过6%,最优结果泄漏量比初始量减小了47%,出口最大速度比初始量降低了36%。
以上结果进一步验证了笔者所构建的径向基神经网络代理模型精确度较高,可以代替仿真模型进行优化设计。
5 结束语
笔者通过数值模拟计算得出泄漏量与进出口的压力比、润滑油黏度、高速转轴与低速转轴的转速和迷宫密封的密封间隙的相对关系,揭示了某风电齿轮箱泄漏特性;构建了径向基神经网络代理模型,选取了设计变量与优化目标,使用非劣分层遗传算法获得了最优解。
研究结论如下:
1)分析了在不同转速和进出口压力比条件下泄漏量数值的变化情况,得出结论:泄漏量与进出口压力比成正比且对泄漏量的影响大,但不受齿轮箱内两个转轴转速的影响;
2)分析了在不同润滑油牌号和温度条件下泄漏量的变化情况,得出结论:工作温度升高,润滑油的动力黏度减小导致泄漏量增大;牌号小的润滑油泄漏量更大;
3)分析了在不同密封间隙条件下泄漏量的变化情况,得出结论:泄漏量随密封间隙的增加而增加;
4)构建了迷宫密封的RBF代理模型,并以其泄漏量和出口最大速度的最小值作为目标函数,采用NSGA-Ⅱ算法获得了最优解;将优化后的参数输入到流体动力学模型中,验证了优化结果的准确有效性,得到了最优结果泄漏量比初始量减小了47%;所得出口最大速度比初始量降低了36%,为迷宫密封的优化设计提供参考。
因此,在后续的研究中,笔者将继续开展风电齿轮箱内迷宫密封其他结构参数的研究,为迷宫密封的泄漏量研究提供理论依据。

