基于数学思维解决“鸡兔同笼”问题

魏媛媛

“鸡兔同笼”是我国古代的一道数学名题，它以富有创意和趣味性的方式体现了代数方法的一般性，对于培养学生的逻辑推理能力具有不可替代的作用。笔者聚焦“鸡兔同笼”问题的教学，从教材编排和教学策略两方面进行分析和阐释。

一、现行多版本教材相关内容编排的差异

目前，“鸡兔同笼”问题在不同版本教材中存在着编排年级不同、例题表达不同、呈现的解决方法不同等差异。这一内容在教材编排中的年级跨度很大，最早安排在沪教版数学二年级下册教材中，最晚安排在苏教版、青岛版、西师大版数学六年级下册教材中。尽管内容编排在年级上跨度很大，但这类问题在不同版本教材中的呈现方式、解决方法是符合特定学段要求和学生认知发展规律的：第一学段主要让学生通过画图和列举，解决数值较小的“鸡兔同笼”问题，初步感知生活中有很多类似的问题；第二学段引导学生解决“鸡兔同笼”问题及其变式题，掌握解决这一类问题的方法，提升用数学的方法解决现实问题的意识；第三学段重点引导学生构建“鸡兔同笼”的数学模型。各个学段都用到了多种方法，关注了方法之间的有机融合。具体内容梳理如左下方表格所示。

二、教学“鸡兔同笼”问题的策略

1.用数学思维思考“眼前问题”

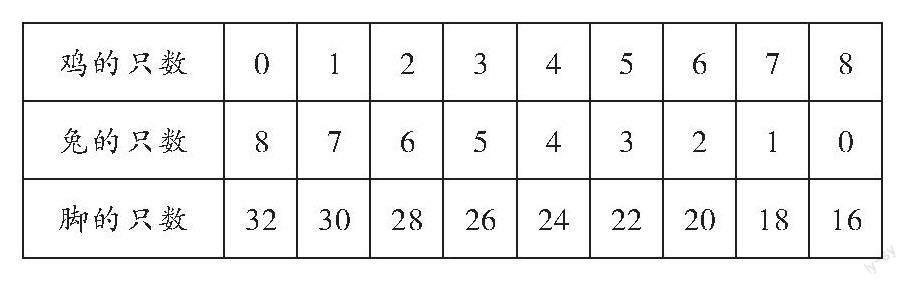
人教版数学四年级下册“鸡兔同笼”问题（例1）如下：“笼子里有若干只鸡。从上面数，有8个头，从下面数，有26只脚，鸡和兔各有几只？”大部分学生看完题目后会猜测有4只鸡、4只兔，并用“4×2＋4×4=24”计算出总脚数。这个答案非常接近题目中的26只，我们只需要微调鸡和兔的只数即可找到答案。因为24只脚比题目要求的26只脚少，所以需要将兔的数量增多，鸡的数量减少。学生再次猜测有3只鸡、5只兔，并用“3×2+5×4=26”计算出总脚数。教师引导学生继续思考，是否还有别的答案符合题目要求。学生发现猜测法在这里不适用了。教师提示学生尝试新思路，用列表法逐一列出如下数据。

假设有8只兔（表第二列），则脚的数量为“8×4=32”只。“32-26=6”只，多6只脚说明兔多了、鸡少了。每只兔比鸡多2只脚，所以“6÷（4-2）=3”只。这3只就是鸡的数量。或者假设有8只鸡（表最后一列），则脚的数量为“8×2=16”只。“26-16=10”只，少10只脚说明鸡多了、兔少了。每只兔比鸡多2只脚，所以“10÷（4-2）=5”只。这5只就是鸡的数量。学生从表中可知，只有“3只鸡、5只兔”这一种答案符合题意。这样教学，让学生通过不断假设、比较、推理、调整的过程发现应用列表法解决问题的规律，积累猜测和推理的经验，并在一一对应的数学思想方法的引领下学会了有序思考，理清了用假设法解决问题的思路。

2.用数学眼光看待“核心问题”

利用列表法、假设法得出答案后，教师提出“为什么是鸡兔同笼而不是鸡鸭同笼？”的问题，学生对此感到迷惑。经过教师引导，他们发现鸡鸭都是一个头、2只脚，“鸡鸭同笼”相当于“鸡鸡同笼”，无法通过头和脚的数量来判断各自的只数，而“鸡兔同笼”则避免了这个问题。

“鸡兔同笼”会出现两种情况。

第一种：已知头数，求脚数。①笼子里有8只鸡，共有多少只脚？（8×2=16只）②笼子里有8只兔，共有多少只脚？（8×4=32只）③鸡兔同笼，共有8个头，共有多少只脚？（不能确定）这3点共同说明：头数确定了，对应的总脚数在一个区间内，如笼中共有8个头时，总脚数在16～32之间，即：已知总头数时，总脚数在全是鸡、全是兔的脚数之间。同时，我们可以发现：笼中的鸡每增加1只，兔就会减少1只，总脚数就会减少2只；反之，笼中的鸡每减少1只，兔就会增加1只，总脚数就会增加2只。

第二种：已知脚数，求头数。①笼子里关着鸡，共有28只脚，一共有几只鸡？（28÷2=14只）②笼子里关着兔，共有28只脚，一共有几只兔？（28÷4=7只）③鸡兔同笼，共有28只脚，笼子里的鸡和兔各有几只？（不能确定）这3点共同说明：当笼子里只有鸡或兔时，告诉我们脚数，马上就能求出头数；当鸡兔同笼时，告诉我们共有28只脚，不能马上确定鸡与兔的只数。但能分析出总头数在7～14之间，即已知总脚数时，总头数在全是鸡、全是兔的头数之间。同时，我们可以发现：笼中的兔每增加1只，需要2只鸡来补充，鸡和兔的总只数就会减少1只；反之，笼中的兔每减少1只，就会多出2只鸡，总只数就会增加1只。

有了前面的分析做基础，学生再看到这样的题目时就不会急着从方法入手寻求答案了，而是会先通过分析数据得知：共有8个头时，总脚数在16～32之间；总脚数是28只，大于中间数24，说明笼中兔多鸡少。学生还发现，鸡和兔关在一起与笼中只有一种动物的情境相比，前者是不确定的，后者是确定的，而假设法能把不确定的信息转化为确定信息，以达到解题目的。

3.用数学语言表达“延伸问题”

当学生理解了利用鸡脚与兔脚的差异性建立的“鸡兔同笼”模型，就可以解决相关的延伸问题。如：在一次军事演习中，红方准备将一个秘密信息设置为“56”送到司令部，如果派遣信使直接将该信息送过去，存在被蓝方抓获从而泄露信息的危险，请你设计一种方案，该方案要满足两个条件：第一，如果信使没有被抓，则红方司令部能顺利得到“56”这个信息；第二，如果信使被抓，则蓝方得不到“56”这个信息。

这个问题乍一看和“鸡兔同笼”问题不相关，但实际上能用“鸡兔同笼”模型来解决。教师可引导学生将这个两位数十位上的数字看作鸡的只数，个位上的数字看作兔的只数，在此基础上分析题目。红方可以派出2名信使，信使A向司令部派送的信息“11”是两种动物头的数量，信使B向司令部派送的信息“34”是两种动物脚的数量。红方司令部在接收到信使A和信使B派送的信息后，利用假设法可以得到鸡和兔的只数，从而知道这个两位数为“56”。蓝方在只抓获1名信使的前提下无法得知“56”这个信息。

解决“鸡兔同笼”延伸问题的关键是找到题目中对应的头的数量和脚的数量，进而用“鸡兔同笼”问题模型解决问题，从而提高学生的抽象思维能力，发展学生的数学核心素养。

（作者單位：武汉大学第一附属小学）

责任编辑  张敏