汽车焊装线滑橇滚体加工误差分析及改进措施

张添孝，陈小芹

（1.广东省粤东技师学院，广东汕头 515078；2.汕头职业技术学院，广东汕头 515078）

0 引言

地面滑橇式输送机是轿车制造厂焊装、涂装、总装自动化生产系统的关键设备[1]，滑橇式随行夹具托起汽车本体沿着生产线线运行，其中滑橇输送机的滚体与橇体底部接触，并通过摩擦力推动滑橇向下一道工序运行。因此，橇体底部支撑及驱动装置为该设备的核心部件，图1 中动力输出部件为安装在支架上的滚体总成，与滑橇长期摩擦接触的是滚体总成上的滚体（图2），其制造精度关系到整个生产线的运行稳定性，影响着各种工序机器人的钻孔、焊接、安装等工艺精度。企业在承接汽车厂焊装生产线滑橇输送机的制造过程中，出现滚体加工返工率较高、生产效率低等问题。为提高产品质量、减少废品、节约材料与人力消耗，解决滚体的质量问题，需要分析找出原因，提出改进措施以保证滚体加工质量和生产效益。

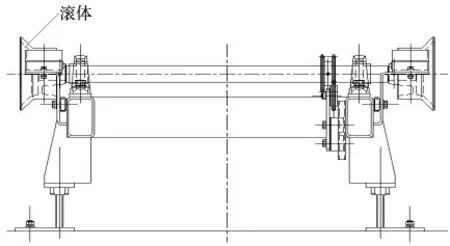
图1 支架及滚体总成

图2 滚体

1 滚体加工工艺

该滑橇输送机滚体坯料为精铸件，材料ZG310-570，双边机加工余量3 mm，外轮廓为变截面回转体，尺寸精度、形状精度和表面粗糙度要求较高，其中与橇体直接接触的踏面外圆Φ140 为关键尺寸，加工中较难达到技术要求。滚体加工工艺见表1。

表1 滚体加工工艺路线

粗加工中因各种原因产生的变形可在精加工中修正，因此主要分析外轮廓精加工工序。滚体外轮廓由圆柱面、圆锥面及凹圆弧过渡面构成，在加工凹圆弧和锥面时由于刀尖圆弧的存在会发生少切，故采用G42 右刀补，并在补偿器中输入刀尖半径及假想刀尖相对于圆头刀中心位置为3，数控系统根据工件轮廓和刀尖半径补偿值自动计算出刀尖圆弧中心轨迹，则编程时不考虑刀尖半径，按图纸所给尺寸编程[2-4]。外轮廓精车程序如下：

N10 G98 G00 X150.0 Z200.0 每分钟进给，刀具移至换刀点

N20 M03 S1000 T0101 M08 主轴正转，1000 r/min，1 号车刀，1 号刀补，切削液开

N30 G00 X140.0 Z-23.0 快速定位靠近起点

N40 G42 G01 X138.0 Z-25.0 F50 定位至起点，建立刀具圆弧半径右补正

N50 G01 X139.98 Z-26.0 加工倒角

N60 G01 Z-88.964 加工Φ140 外圆

N70 G02 X141.464 Z-90.732 R2.5 加工R2.5凹圆弧

N80 G01 X200.0 Z-120.0 加工锥面

N90 G01 Z-124.0 加工Φ200 外圆

N100 G01 X206.0 退刀

N110 G40 G00 X150.0 Z150.0 退刀至安全点，取消刀具圆弧半径补正

N130 M09 M30 切削液关，程序结束

2 测量数据及直方图分析

在生产过程中因外轮廓尺寸达不到精度要求而出现较多返工，为分析误差性质并寻求针对性解决措施，特对本批次调整法生产的800 套滚体抽检，取样N=80 组。滚体外圆Φ140 实测数据偏差即实测尺寸与基本尺寸之差如图3 所示。

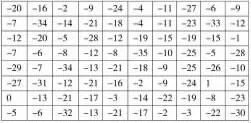
图3 尺寸偏差（μm）

图3 得到的是一组杂乱无章的数据，只有通过数据整理、直方图统计分析才能揭示其内在的规律性。首先对数据合理分组并确定组距，根据Sturges 公式计算组数，K=1+3.32lgN≈7.3，向上圆整，取组数K=8，图3 中的尺寸偏差最大值xmax=1 μm、最小值xmin=-35 μm，则组距d==4.5 μm，圆整为量具最小分辨值的整数倍，取d=5 μm，获得了表2 所示的频数分布。

表2 频数分布

根据频数分布表数据，为了使分布图更好地反映外圆加工精度而不受组距和样本容量的影响，以工件尺寸偏差为横坐标，以频率密度为纵坐标绘制图4 直方图，连接各矩形顶部中点，得到该批滚体尺寸的实际分布曲线。由直方图可以看出，工件尺寸分布出现了双峰并有一个分布范围，尺寸偏大偏小者较少，大多数据中，呈不对称分布，总体偏大。

图4 直方图及实际分布曲线

3 分布图分析

从图4 上的分布曲线可以清晰看出误差分布范围和偏离情况，对比理论分布曲线还可以确定误差性质、产生原因及工序工艺能力，预测废品率，发现设备的运行情况以及工人操作习惯等，从而提出有针对性的技术措施，现对分布图作如下分析：

3.1 判断加工误差性质

正态分布的4 个基本特征是单峰性、对称性、有界性和补偿性，滚体尺寸实际分布曲线出现双峰，尺寸偏差总体偏大且不对称，未完全服从正态分布，说明车削过程中存在系统性误差。

出现双峰主要是由于两台机床加工，将加工后的滚体混在一起，不但常值系统性误差不同，而且机床的精度也不同，即随机性误差的影响不同，导致分布曲线的峰高不等。双峰分布实质上是两组分布曲线的叠加，即在随机误差中混入常值系统误差，每组有各自的分散中心和标准偏差。尺寸偏差不对称分布尺寸并且总体偏大，是由于在加工过程中，操作者主观上为了避免产生不可修复废品，加工滚体外圆时宁大勿小，过于偏大则有超出公差的趋势，如果加工条件稍有变动，就会出现可修复的不合格品，返工量加大，降低加工效率。此外在加工过程中由于刀具的磨损，随着加工的进行，尺寸分布中心在均匀移动，因此形成平顶分布有一段曲线概率相等，平峰分布实质上也是源于在随机性误差中混入了变值系统误差。

3.2 确定工序的工艺能力

工序的工艺能力是否满足加工精度的要求，可以用工序能力系数Cp表达，并据此将工艺等级由高到低分5 级，最高为特级，最低为4 级。本工序的工艺能力系数，工艺等级为3 级，说明工艺能力明显不足，加工中会产生少量不合格品。由于存在系统误差，即分布中心和公差中心不重合，则需要满足时才不会出废品。本工序需要进行工艺调整以提高工艺能力。

3.3 估算合格品率

取偏差平均值x¯为对称中心，通过坐标变换将实际分布曲线转化变为标准分布曲线。在标准分布曲线上不同区间所包含的面积，表征了随机变量落在该区间的概率，可用于计算工件的合格品率。令构建面积函数（fz）。在（，δma）x区间，查表可知，f（z1）=0.449 5，故可修复废品率：Q1=0.5-f（z1）=5.05%。在（δmin，）区间，≈2.65，查表可知，f（z2）=0.4957，故不可修复废品率：Q2=0.5-f（z2）=0.43%。合格品率：100%-Q1-Q2=94.52%。返修后合格品率：100%-Q2=99.57%。由以上分析可知，目前工件返修率高，严重影响生产效率，亟需改进。

4 减小尺寸误差的技术措施

数控车削加工误差一方面源于数控车床本身老化磨损、自身零部件装配误差等，另一方面源于机床及工件的热变形、切削力的变化、振动、刀具的磨损、工件的装夹、加工工艺及编程处理不当、操作者技术水平参差不齐等因素。从以下5 个方面着手采取相应的技术措施：

4.1 改善作业流程

由于两台机床同时生产，设备系统误差和操作人员误差使测量数据呈非正态分布，出现双峰，偏差过大，工序工艺能力偏低。故对作业流程进行改善：精加工阶段可采用两台机床流水作业，一台精车外轮廓，一台精车内孔，在生产设备和人员不变的前提下，减小系统误差及偏差分散范围。

4.2 编程反向补偿

轴类零件车削时往往尺寸偏大，为了弥补加工过程中的偏差，可采用编程反向补偿的方法，即通过编程时多吃刀而进行矫正。滚体外径实测偏差平均值偏大公差带中心值约4.6 μm，编程时可将语句N60 修改为：G01 X139.978 Z-26.0，实现编程反向补偿，降低滚体返工量。

4.3 减小对刀误差

试切法对刀误差主要是由测量误差造成的，此外静态测量动态加工，刀具与工件受到切削力与振动外力作用，也会使加工尺寸出现偏差，故应定期校验量具精度及检测维护保养机床。在测量滚体外径时可先用游标卡尺测出范围值，然后用外径千分尺测出精确值，操作细心规范，并及时进行刀补调整，从而减小对刀误差。

4.4 刀具磨损补偿

车削过程中车刀的磨损必然会使同一批加工的滚体尺寸前后不一致，分散范围增大，从而产生变值系统误差。可在初始精车滚体时按先后加工顺序编号逐个测量直径，比较理论值直径和实测值直径，以二者相减得到的磨损值为纵坐标，滚体加工编号为横坐标，做出点图，从点图上获得刀具磨损规律，在后续加工零件时进行刀具磨损补偿，将磨损值输至X 方向磨耗内，并需要时常测量修正此偏差。一般刀具使用前期和后期磨损快，中期磨损慢，因此在加工过程中每一个零件都必须测量，并在刀具后期磨损前更换刀片。

4.5 空行程编程误差补偿（减小机械间隙误差）

刀架在X 轴方向的进给精度影响着滚体外轮廓径向尺寸偏差。每次换向时，刀架的实际运动量与理论值就会产生误差。采用空行程编程误差补偿，始终使丝杠副在同一侧接触，即在拐点处回程间隙最明显的位置，小距离反向抬刀或收刀，然后再正向进给，来同步消除丝杠在该处产生的回程间隙累积误差，避免工件拐点处被刀具碰伤，提高机床的加工精度和加工质量，避免机械方法增大预紧力引起的阻力增大和调整困难。

采取以上措施后，产品返工率降低，误差正态分布曲线由双峰变为单峰，产品精度趋于稳定。

5 结束语

要在数控车床上加工高精度、批量的产品（零件），就要很好地分析各种误差产生的原因以及误差控制的方法，本文根据抽检数据，以及滚体实际加工情况，就公差数据分散、返工量大的原因进行分析，提出了误差控制的具体方法。实践证明，这些方法非常实用易行，能很好地提高零件车削的质量和加工效率。此外，通过分布曲线分析，还可以及时发现设备的运行情况，以及工人操作习惯，针对设备长时间运行出现精度下降问题，及时提出检修方案和计划，针对工人操作问题则可及时纠正或定期培训以提高理论和专业技术水平。