基于IWOA-SVM的变压器绕组热点温度预测
马成,罗亭然,刘闯,卢银均
(1.国网湖北省电力有限公司荆州供电公司,湖北 荆州 434000;2.国网湖北省电力有限公司荆门供电公司,湖北 荆门 448000)
0 引 言
变压器在长期运行过程中,热老化是造成变压器绝缘性能下降的重要原因,根据6 ℃法则,变压器内部温度超过80 ℃时,温度每增加6 ℃,变压器老化速率增加1倍[1-3]。绕组热点温度是衡量变压器健康状态和老化特性的重要指标,但由于技术限制,目前绕组热点温度无法直接测量[4-5],因此对变压器绕组热点温度预测方法进行研究,实现绕组热点温度精准预测具有重要的现实意义。
现有热点温度估算方法主要有导则法[6]、有限元法[7]和智能计算法[8]。导则法主要是根据变压器运行技术规范中的经验公式估算的,由于经验公式不够完善,导致导则法误差较大。有限元法主要是基于温度场仿真计算得出的,运算过程复杂,估算效果一般。智能计算法是基于一些智能算法实现的,目前已有一些绕组热点温度智能预测方法被提出。张军提出了一种基于遗传编程算法优化归一化自适应滤波的绕组热点温度预测模型,采用算例分析对该方法的有效性进行了验证[9]。李世倩将粒子群算法和最小二乘法相结合建立预测模型,利用顶层油温和对流换热系数对绕组热点温度进行估算,提出了一种新型绕组热点温度预测方法[10]。韩祥采用可变步长、自动清除机制对人工鱼群算法进行改进,解决了人工鱼群算法收敛性能差的缺陷,采用改进鱼群算法(improved fish school algorithm,IFSA)优化支持向量机(support vector machine,SVM)的参数,提出了一种基于IFSA优化SVM的绕组热点温度预测方法,提高了绕组热点温度预测精度[11]。上述智能计算法在建立预测模型时,均未对绕组热点温度的主要特征量进行筛选,导致模型计算量大,绕组热点温度预测效果不理想。
本文对引起绕组热点温度变化的特征量进行灰色关联分析,根据灰色关联度确定绕组热点温度预测的主要特征量,采用改进鲸鱼优化算法(improved whale optimization algorithm,IWOA)对SVM的惩罚参数和核宽度参数进行优化,建立基于IWOA-SVM的变压器绕组热点温度预测模型,采用实际算例对该模型的实用性和有效性进行验证。
1 灰色关联分析
绕组热点温度变化与变压器负载电流、油温和环境因素有关,在进行绕组热点温度预测时,这些影响因素统称为特征量,本文利用灰色关联分析[12]确定绕组热点温度与特征量之间的定量关系,主要步骤如下:
1)确定目标序列。设绕组热点温度为目标序列y(k),k=1,2…n,特征量序列为xi={xi(k)|i=1,2…m},其中,n和m分别表示样本容量和特征量个数。
2)数据无量纲化。由于各特征量的单位和数量级不同,不便于计算,采用归一化公式对数据进行无量纲处理,具体如下:
(1)

3)计算目标序列与特征量之间的关联系数。计算公式如下:
(2)
式中:ξi(k)为特征量i在k时刻的关联系数,取值范围为[0,1],当ξi(k)<0.5时,表示目标序列与特征量i的关联性很弱;当0.5≤ξi(k)<0.7时,表示目标序列与特征量i的关联性一般;ξi(k)≥0.7时,表示目标序列与特征量i的关联性很强;ρ为辨别系数,取值通常为0.5。
4)计算平均关联度。对关联系数取平均值即可得到特征量i的平均关联度ri,ri计算公式为
(3)
式中:ri的取值范围及关联性判断与ξi(k)相同。
2 改进鲸鱼算法
2.1 鲸鱼优化算法
鲸鱼优化算法(whale optimization algorithm,WOA)是在2016年提出的一种算法,WOA算法的原理是座头鲸的狩猎行为,其狩猎过程主要包括包围、攻击和搜寻3个阶段[13]。
1)包围阶段。座头鲸发现猎物后会迅速将猎物包围,设猎物位置为全局最优位置,则座头鲸个体均朝着猎物位置移动,并采用下列公式更新位置,具体为
X(t+1)=X*(t)-A·D
(4)
D=|C·X*(t)-X(t)|
(5)
式中:A、C均为座头鲸位置向量系数,X*(t)为猎物位置,X(t)为座头鲸当前位置,X(t+1)为座头鲸下一次迭代时的位置,D为座头鲸与猎物之间的距离,t为当前迭代次数。
A、C的计算方法分别如下:
A=2a×r1-a
(6)
(7)
C=2·r2
(8)
式中:a为控制因子,tmax为迭代次数上限,r1、r2为[0,1]之间的随机数。
2)攻击阶段。座头鲸利用自身产生的螺旋气泡攻击猎物,该过程中鲸鱼位置更新公式为
X(t+1)=X*(t)+D·eblcos(2πl)
(9)
式中:b为螺旋系数;l为[0,1]之间的随机数。
鲸鱼包围猎物或是采用气泡攻击猎物通过概率p进行选择,由此可以得到
(10)
3)搜寻阶段。鲸鱼找寻猎物的过程中,除了向最优位置靠拢外,还会展开随机搜索,当|A|≥1时,鲸鱼位置更新公式为
X(t+1)=Xrand(t)-A·D
(11)
D=|C·Xrand(t)-X(t)|
(12)
式中:Xrand(t)为鲸鱼随机搜索时的位置。
2.2 改进鲸鱼算法
WOA算法原理简单,容易实现,但在寻优过程中易陷入局部最优[14],为了使算法的优化性能更好,采用下列两种策略对WOA算法进行改进。
1)余弦调整控制因子。WOA算法在寻优过程中的全局搜索和局部搜索是由向量系数A控制的,而A的值取决于控制因子,由式(7)可知,WOA算法的控制因子是线性变化的,这是造成算法在迭代后期局部搜索性能不足的原因,本文采用余弦变化对控制因子进行调整,具体如下:
(13)
由式(13)可知,迭代前期的控制因子缓慢减小,算法可以充分进行全局搜索,到了后期,控制因子快速降低,算法局部搜索能力增强。
2)引入自适应权重系数。为了避免算法陷入局部最优和增强算法跳出局部最优的能力,在攻击阶段座头鲸位置更新公式中引入自适应权重因子,使攻击阶段的效率提升,加快算法收敛,具体如下:
X(t+1)=X*(t)+w(t)·D·eblcos(2πl)
(14)
(15)
式中:w(t)为自适应权重因子。
3 SVM回归原理
SVM是一种非线性机器学习算法,适用于容量较小、信息相对匮乏的样本数据[15]。由于在工程实际中,绕组热点温度无法直接测量,其样本数据都是通过变压器高压试验获得的,数据容量相对较小,为此本文采用SVM作为绕组热点温度预测的工具。SVM的回归拟合函数如下:
f(x)=ωφ(x)+b
(16)
式中:x为支持向量,ω为权向量;b为拟合误差。
通过对权向量和拟合误差反复训练,并采用拉格朗日乘子进行转化,式(16)最终可变为

(17)

利用SVM解决非线性回归问题时,要求核函数的泛化性能好,为此本文采用径向基核函数,其表达式为
(18)
式中:σ为核系数。
4 基于IWOA-SVM的绕组热点预测模型
SVM的预测精度受其惩罚系数C和核系数σ影响较大,为了提高绕组热点温度预测精度,利用灰色关联分析确定支持向量,采用IWOA算法对SVM的参数进行优化,建立基于IWOA-SVM的变压器绕组热点温度预测模型,图1所示为IWOA-SVM模型流程,主要建模步骤如下:
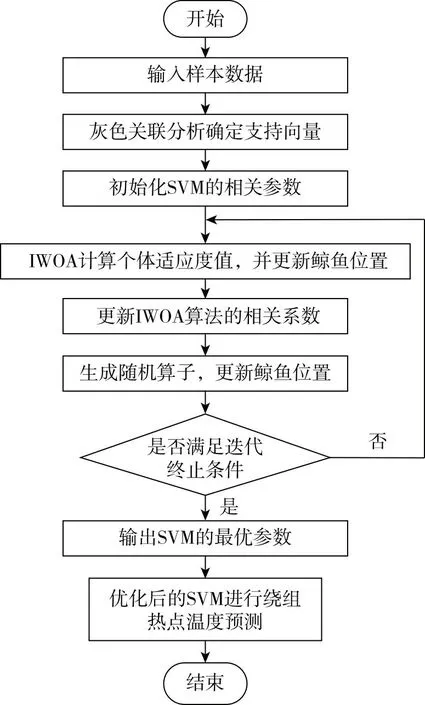
图1 IWOA-SVM模型流程
1)输入样本数据,对样本数据进行灰色关联分析,根据分析结果确定支持向量。
2)初始化SVM参数,设置惩罚系数C和核系数σ的初值及搜索范围,计算初始适应度值。
3)设置IWOA算法的相关参数,包括座头鲸种群规模、算法最大迭代次数等。
4)初始化鲸鱼种群,将惩罚系数C和核系数σ作为猎物,利用IWOA算法对C和σ进行寻优,并计算鲸鱼个体适应度值,适应度函数采用SVM输出结果的均方误差,其计算公式为

(19)
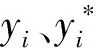
5)选择适应度值最好的个体作为当前最优解,并更新鲸鱼位置,通过迭代不断更新当前最优解。
6)判断迭代结束条件是否满足,若满足,则输出C和σ的最优解,否则,返回上一步骤。
7)将最优解赋给SVM,即可利用SVM预测绕组热点温度。
5 算例分析
采用文献[16]中的变压器监测数据进行仿真分析,变压器型号为SFPSZ4-120000/220,其额定容量为120 MVA,额定电压为220 kV,数据采样间隔为1 h/次,共100组样本,每组样本包括有功功率x1、无功功率x2、负载电流x3、顶层油温x4、风速x5、湿度x6和环境温度x7等特征量及其对应的绕组热点温度,具体如图2所示。

(a)有功功率
对各特征量进行灰色关联分析,计算结果如表1所示,由表1可知,7个特征量与绕组热点温度的相关性从强到弱的排序结果为x3>x1>x4>x7>x6>x2>x5,且排在前四特征量(负载电流x3、有功功率x1、顶层油温x4和环境温度x7)的关联度大于0.7,可见这4个特征量和绕组热点温度具有强关联性,因此将负载电流、有功功率、顶层油温和环境温度作为绕组热点温度预测的特征量。

表1 灰色关联分析结果
将负载电流、有功功率、顶层油温和环境温度4个特征量作为输入量,绕组热点温度作为输出量,组成新的样本数据,按照9∶1的比例划分样本数据,即训练集和测试集样本容量分别为90组和10组,在MATLAB软件中建立IWOA-SVM模型,利用训练集进行训练,采用IWOA算法对SVM的惩罚系数C和核系数σ进行优化,IWOA算法的收敛曲线如图3所示,图3中同时给出了WOA算法的收敛曲线作为对比,由图3可知,IWOA算法收敛至最优解时的迭代次数更少,适应度值更小。
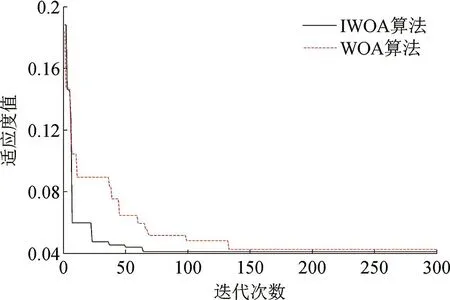
图3 收敛曲线
表2给出了IWOA算法和WOA算法找到最优解时的各项参数对比,对比表2中的数据可以看出,IWOA算法在迭代次数、最优适应度值和收敛时间方面均优于WOA算法,可见采用余弦调整控制因子和引入自适应权重系数两种策略改进后的鲸鱼算法优化性能显著提升。

表2 IWOA算法和WOA算法对比
模型训练完成后,采用IWOA-SVM模型对测试集中的绕组热点温度进行预测,为了对比本文所提方法的有效性,采用文献[11]中的IFSA-SVM模型、文献[17]中遗传算法(genetic algorithm,GA)优化SVM模型(GA-SVM)和文献[18]中灰色神经网络(grey neural network,GNN)模型进行对比分析,4种方法对测试集绕组热点温度的预测结果如图4所示,IWOA-SVM模型的预测结果的绕组热点温度变化趋势与实际值基本一致,预测结果也更接近实际值。

图4 4种模型对测试集的预测结果
采用均方根误差εRMSE、决定系数R2和平均相对误差εMAPE对3种方法的预测效果进行评价,εRMSE、R2和εMAPE的计算公式分别为
(20)
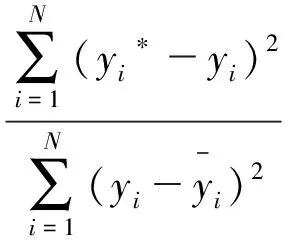
(21)
(22)

表3给出了4种不同模型预测结果的各项指标,本文所提IWOA-SVM模型的均方根误差为1.21 ℃,决定系数为0.897,平均相对误差为2.14%,3项指标均比另外2种方法获得的指标更好,可见本文方法在进行绕组热点温度预测时的波动性更小、拟合度更高、预测结果更准确,验证了本文所提绕组热点温度预测方法的实用性和有效性,该方法也为变压器绕组热点温度预测提供了一条新思路。

表3 4种模型对比
6 结 语
本文采用灰色关联分析法对引起绕组热点温度变化的特征量进行分析,根据分析结果确定负载电流、有功功率、顶层油温和环境温度为绕组热点温度预测模型的输入量。利用余弦调整控制因子和引入自适应权重系数两种策略对WOA算法进行改进,采用IWOA优化支持向量机参数,建立了基于IWOA-SVM的变压器绕组温度预测模型,采用实际运行变压器监测数据进行仿真分析,并与现有绕组热点温度预测方法对比,结果表明,本文所提方法在进行绕组热点温度预测时的波动性更小、拟合度更高、预测结果更准确,验证了该方法的实用性和有效性,该方法也为变压器绕组热点温度预测提供了一条新思路。

