Enhanced prediction of anisotropic deformation behavior using machine learning with data augmentation
Sujeong Byun ,Jinyeong Yu ,Seho Cheon ,Seong Ho Lee ,Sung Hyuk Prk ,Tekyung Lee,∗
a School of Mechanical Engineering, Pusan National University, Busan 46241, South Korea
b School of Materials Science and Engineering, Kyungpook National University, Daegu 41566, South Korea
Abstract Mg alloys possess an inherent plastic anisotropy owing to the selective activation of deformation mechanisms depending on the loading condition.This characteristic results in a diverse range of flow curves that vary with a deformation condition.This study proposes a novel approach for accurately predicting an anisotropic deformation behavior of wrought Mg alloys using machine learning (ML) with data augmentation.The developed model combines four key strategies from data science: learning the entire flow curves,generative adversarial networks (GAN),algorithm-driven hyperparameter tuning,and gated recurrent unit (GRU) architecture.The proposed model,namely GANaided GRU,was extensively evaluated for various predictive scenarios,such as interpolation,extrapolation,and a limited dataset size.The model exhibited significant predictability and improved generalizability for estimating the anisotropic compressive behavior of ZK60 Mg alloys under 11 annealing conditions and for three loading directions.The GAN-aided GRU results were superior to those of previous ML models and constitutive equations.The superior performance was attributed to hyperparameter optimization,GAN-based data augmentation,and the inherent predictivity of the GRU for extrapolation.As a first attempt to employ ML techniques other than artificial neural networks,this study proposes a novel perspective on predicting the anisotropic deformation behaviors of wrought Mg alloys.
Keywords: Plastic anisotropy;Compression;Annealing;Machine learning;Data augmentation.
1.Introduction
Mg alloys have drawn substantial attention in the aerospace and automotive industries because of their high strengthto-weight ratios.They also have potential applications in biomedical and electronic devices because of their biocompatibility,biodegradability,and low density [1–4].However,in addition to their low strength and formability,Mg alloys exhibit anisotropic deformation behavior,wherein their mechanical properties significantly vary with the loading direction.This anisotropy is a result of the unique hexagonal closepacked structure and subsequent grain orientation of Mg,and it leads to the selective activation of deformation mechanisms depending on the loading condition[5–9].Accurate prediction and control of anisotropic deformation behavior are crucial because they can significantly impact the overall performance and durability of Mg alloy components.
Typically,constitutive analysis is used to estimate the anisotropic deformation behavior of Mg alloys [10–15].This approach correlates physical quantities based on a fundamental physical model and subsequently adjusts them using numerical constants for empirical regression.Although constitutive analysis provides valuable information for characterizing the deformation mechanisms,it often relies on several assumptions,numerical fittings,and even manual adjustments of constants for practical implementation,as discussed in detail below.These inherent limitations of constitutive approach highlight the necessity of an alternative method for predicting the anisotropic properties of wrought Mg alloys.
Currently,researchers are paying considerable attention to machine learning(ML)techniques because of their functionality with respect to powerful data analysis and predictivity for multivariant nonlinear problems.Numerous studies have used this technique to interpret the thermomechanical properties of Mg alloys [16–19].For example,Sani et al.[16]conducted a comparative study between an artificial neural network(ANN)and constitutive analysis in predicting the high-temperature deformation behavior of cast Mg-Al-Ca alloys.Wang et al.[17]utilized an ANN to improve processing maps describing the hot-deformation behavior of the AZ91 Mg alloy.Yu et al.[18]employed ML techniques to precisely estimate the radical temperature change caused by a short-duration electropulse in ZK60 Mg alloy.Moreover,they compared ML algorithms in terms of both accuracy and prediction resources,wherein the extreme gradient boosting algorithm achieved a 1000-fold acceleration in the learning rate compared to that of the ANN.Similarly,Xu et al.[19]compared a support vector machine algorithm with an ANN to estimate the tensile properties of an AZ31 Mg alloy.
To the best of our knowledge,only two studies have used ML to predict the severe anisotropy of deformation behavior for wrought Mg alloys.Our previous model [20]was the first to use an ANN for this purpose.The predictability of this model was better than those of other regression methods,including multiple linear regression (MLR) and shallow ANN.Zhang et al.[21]recently developed another ANNbased model that correlated the texture of the AZ31 Mg alloy with its tensile properties.Although this model provides new insights into texture-based estimation,it exhibits high prediction errors up to 20 % for YS and 10 % for the elongation to failure (EL),respectively.
There is scope for the further improvement of the accuracy of ML predictions from the viewpoint of data science.This study proposes a novel ML-based predictive model specifically designed to predict the anisotropic deformation behavior of wrought Mg alloys.This model was constructed based on four key strategies to enhance model accuracy.First,it learns the data of the entire flow curve rather than the summarized mechanical properties (e.g.,YS and EL) to increase the size of the training dataset.Second,for the same purpose,a data augmentation technique using generative adversarial networks(GAN)is utilized.Third,hyperparameter tuning is determined by an algorithm,instead of the trial-and-error method adopted in previous studies.Lastly,the developed model substitutes an ANN with a recurrent neural network (RNN),expecting a better estimation of the time-series data of the flow curves.The developed model is extensively evaluated under various scenarios,including interpolation,extrapolation,and datasets of limited size to ensure its robustness and reliability.
2.Data acquisition and preprocessing
This study investigated the ZK60 Mg alloy with a chemical composition of 5.74 Zn,0.51 Zr,0.02 Si,0.02 Al,0.03 Cu,and balanced Mg (numbers in mass percentage).The cylindrical ingots were produced using induction melting with a diameter of 26 mm and a length of 500 mm.They were homogenized at 673 K for 10 h,air-cooled,and then reheated to the same temperature for a multi-pass caliber rolling.The caliber rolling consisted of six deformation passes with the total area reduction of 84 %.The caliber-rolled rods were subsequently annealed in an electric furnace at 473–673 K for 0.5–3 h,followed by air cooling to room temperature.The detailed rolling procedures are described in the authors’previous studies [7,22,23].
Compressive deformation properties of ZK60 Mg alloy were obtained using a universal mechanical testing machine at a constant cross-head speed of 1 mm min-1at room temperature.Cylindrical samples were machined from caliberrolled rods that were 6 mm in diameter and 9 mm in height based on the ASTM-E9 standard.The heights of the samples were aligned with either of the following directions to evaluate the anisotropic deformation behaviors: rolling direction(RD),transverse direction (TD),or normal direction (ND).The sample was rotated by 90° per caliber-rolling pass,leading to an alternation between the two coordinate axes on the cross-section.Accordingly,the terms “TD” and “ND” in this work indicate the coordinate system for the final pass of caliber rolling.
Fig.1 depicts the specific experimental conditions used to construct the training and test datasets for ML.Three flow curves were acquired from the compressive tests of the asrolled alloy along RD,TD,and ND.Nine RD flow curves were obtained under 3×3 annealing conditions,encompassing temperatures of 473,573,and 673 K,each for durations of 0.5,1,and 3 h.Similar conditions were applied to TD and ND flow curves,except for the annealing at 673 K for 1 h,leading to the accumulation of 16 flow curves.In addition,the RD flow curve used in a prior investigation [24]was included in the database;the result was obtained after annealing at 523 K for 1 h.Consequently,the current database comprises 29 flow curves with 94,240 instances.This asymmetric database provided valuable insights into this research,as further discussed in Section 5.3.
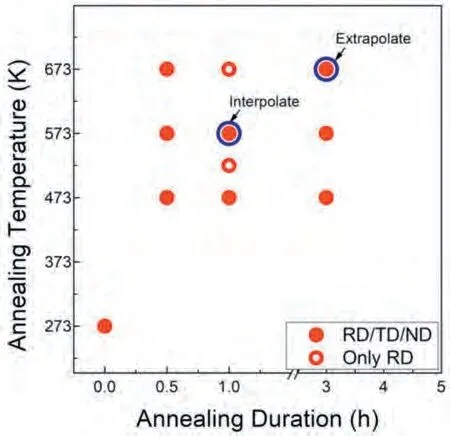
Fig.1.Annealing conditions for experimental data used in the current study.The empty dots indicate the annealing conditions,under which the sample was compressed along only RD.The blue circles indicate the test dataset for interpolation and extrapolation.The datum at zero duration indicates the as-rolled (i.e.,unannealed) condition.
Each instance involved five features: annealing temperature,annealing period,loading direction,engineering strain,and engineering stress.Three loading directions were allocated to integers ranging from 1 to 3.Subsequently,the entire dataset was standardized using an average and standard deviation to minimize unnecessary interference by the range of features.
This study designed two types of predictive scenarios (i.e.,interpolation and extrapolation) to extensively evaluate the performance of the developed model.Each scenario has its own test datasets for the RD and ND flow curves,because they exhibited the most distinct differences and were thus the most challenging to predict (Fig.1).The interpolated test dataset corresponded to the flow curves annealed at 573 K for 1 h,enabling a direct comparison between the present method and the previous ANN model [20].The extrapolated test dataset was set as the flow curve annealed at 673 K for 3 h,which was expected to be the most difficult to predict owing to the largest variation in flow behaviors across all experiments.Additionally,the developed ML model was trained with an abridged training dataset (i.e.,10 % of the original dataset) to create a harsh environment for prediction.To achieve this,the original training dataset was equally divided into ten categories,nine of which were excluded from the subsequent ML process.Table 1 summarizes the prediction conditions used in this study.
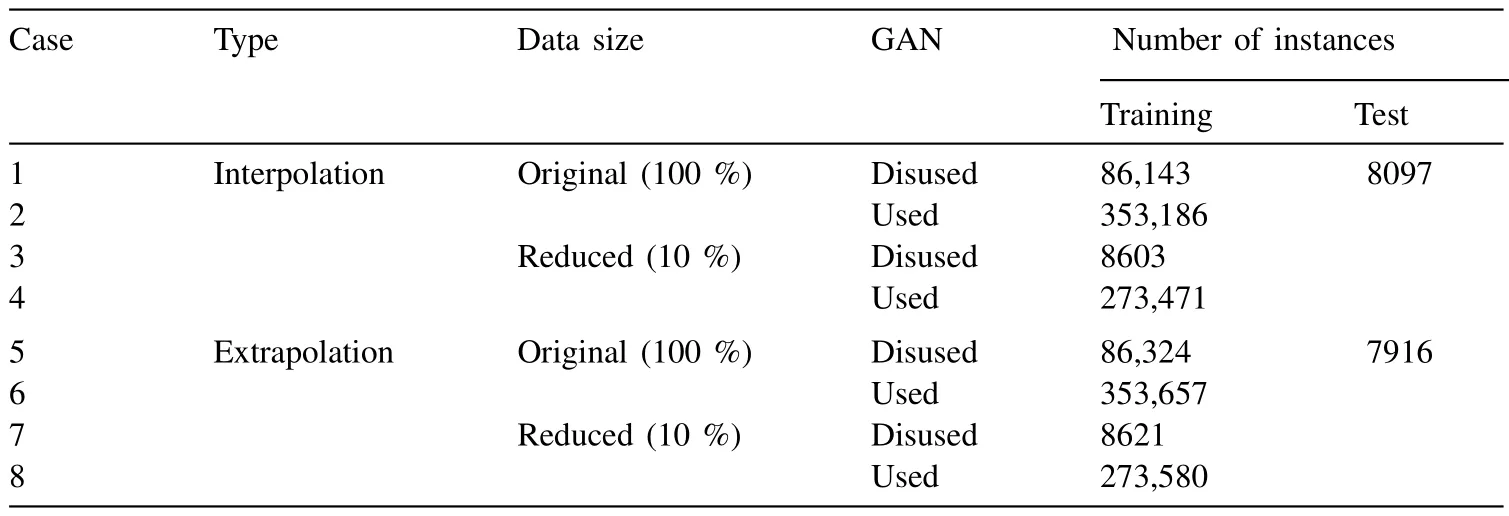
Table 1 Predicting conditions and number of instances used in this study.
3.Machine learning
3.1. Selection of ML models
The authors explored a wide variety of ML models in pursuit of the research objective,including MLR,shallow ANN,DNN,random forest (RF),extreme gradient boosting (XGB),light gradient-boosting machine (LGBM),gated recurrent unit(GRU),and long short-term memory (LSTM).The first three were investigated in our previous work [20]with the conclusion favoring DNN due to its superior predictive performance.As a result,DNN was selected as one of three ML models for this study.Ensemble ML models using a decision tree (e.g.,RF,XGB,and LGBM) are effective for a certain problem.However,they exhibited comparable or even lower performance when applied to predicting sequential data in literature[18,25–29],leading to their exclusion from this research.
RNN represents an advanced ANN architecture designed to perceive sequential data using recurrent connections working as memory [30].LSTM and GRU are the most widely employed RNN models,of which the latter was incorporated into this study due to its faster and superior performance in estimating Al6061 alloy behavior [31].This model resolves the vanishing gradient issue of traditional RNN by adopting gating units to modulate information flow [32].The authors developed an ML model,namely ‘GAN-aided GRU’,by training an optimized GRU model with data augmented through GAN.Hence,this study compares the GAN-aided GRU model with two advanced ML models (i.e.,DNN and GRU) and traditional constitutive approaches.
3.2. ML framework
GAN is a deep-learning architecture that generates synthetic data resembling genuine data [33].It is composed of two competing neural networks,denoted as a generator and a discriminator.False samples are created by the generator and then detected by the discriminator.The repeated opposition improves the overall performance of the GAN model,causing the generated data to be indistinguishable from the original data.
In this study,a GAN was adopted for data augmentation,in which the strain and stress were set as the output variables of the generator and the input variables of the discriminator.Both models have a multilayer perceptron structure with 60 units within a single hidden layer.The leaky rectified linear unit [34]was employed as the activation function for the input and hidden layers,and an exponential linear unit [35]was used for the output layer,based on a preliminary comparative study.Stochastic optimization was performed using the adaptive moment estimation [36].The learning rate was set to be 5×10-4.The dropout method [37]was employed to avoid overfitting.The GAN generated 104instances from the training dataset for each flow curve.The generated data with a strain higher than EL per curve were excluded from the subsequent ML process to increase the prediction accuracy.As a result,the training dataset approximately quadrupled through the data augmentation,with deviations depending on the predicted conditions.The detailed sizes of the training datasets for each condition are listed in Table 1.
The GRU model employed in this study had four input features: the annealing temperature,annealing period,loading direction,and strain.It also exhibits a single output feature of stress.The hyperbolic tangent and adaptive moment estimation were used as the activation function and optimization algorithm,respectively.Meanwhile,the DNN model for comparison underwent optimization in the authors’ previous study[20].It shared the identical input and output features with the GRU model.The rectified linear unit,mean squared error,and adaptive moment estimation were adopted for the activation function,loss function,and optimization,respectively.The dropout routine was omitted in both models because it had marginal impact on enhancing a model performance in initial assessments.The hidden structure and learning rate for each condition were determined through the hyperband optimization [38].
Model accuracy was verified in terms of coefficient of determination (R2) and root mean square error (RMSE),defined as follows:
where,yis an experimental value,is an average value,is an estimation,andnis the total number of instances.The higher model accuracy is indicated by either a higherR2close to 1 or a lower RMSE value.
Finally,this study implemented Shapley additive explanations (SHAP) [39]for detailed analysis.SHAP is an ML method inspired by game theory,which measures the responsibility of a given feature by comparing changes in the model output.The SHAP analysis yields a quantified contribution of individual features to the prediction,termed the SHAP value.The feature information and predicted results were used for SHAP analysis using the deep explainer module.All code was generated using Python ver.3.9 and implemented in Tensor-Flow ver.2.7.0 [40].
4.Results
Fig.2 depicts the flow curves of the caliber-rolled Mg alloy under RD,TD,and ND compressions,which significantly varied.The RD and TD flow curves exhibited a sigmoidal morphology (Fig.2a and b).The strain hardening rate rapidly increased in the early stage of deformation,as characterized by the concave-upward curve,and then decreased on further straining.The RD flow curves showed a larger curvature compared to that of the TD.By contrast,the ND flow curves demonstrated the concave-downward morphology across the entire analysis range,indicating a monotonic reduction of strain hardening rate (Fig.2c).These differences were attributed to the selective activation of deformation mechanisms as discussed in Section 5.1.
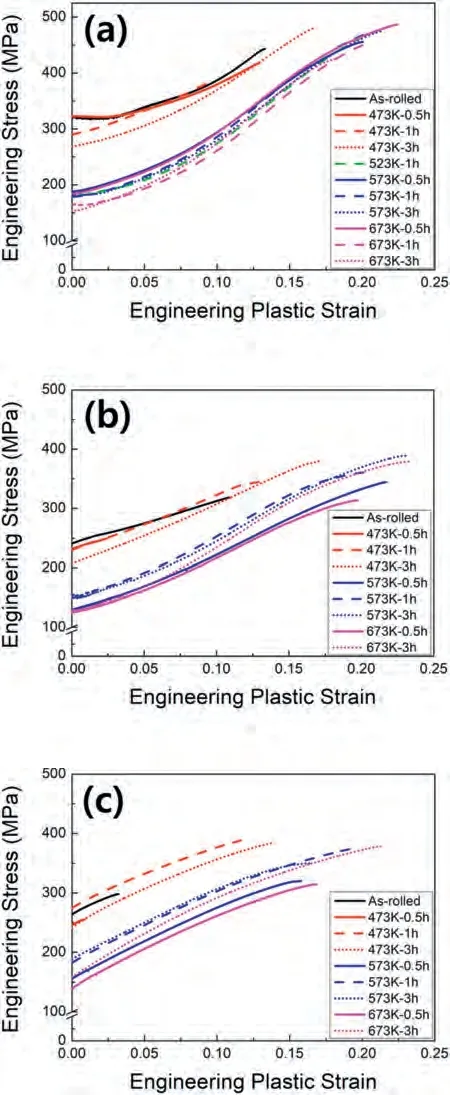
Fig.2.Experimental data used for ML: 29 flow curves of caliber-rolled and annealed ZK60 Mg alloys under compression along (a) RD,(b) TD,and (c)ND.The legends present the annealing temperature and time for each curve.
Fig.3 shows the comparison between the experimental data and the interpolation prediction based on the two methods(i.e.,with and without data augmentation using the GAN).The GRU model without data augmentation presented an accurate prediction of the RD flow curve with a low RMSE(2.97 MPa),whereas the predictivity was degraded for the ND flow curve with a higher RMSE (16.72 MPa).TheR2value for ND (0.91) is significantly lower than that for RD(0.99).These results propose overfitting towards RD compression when the prediction relies on the GRU alone.Notably,integrating a GAN with a GRU resolves the overfitting issue.This GAN-aided GRU model remarkably improved the predictivity for both RD and ND compressions compared to the GRU alone.In particular,RMSE for ND prediction was considerably reduced from 16.72 to 1.60 MPa,whileR2increased from 0.91 to 0.99 (Fig.3b).This improvement is discussed in more detail along with other predictive approaches in Section 5.2.
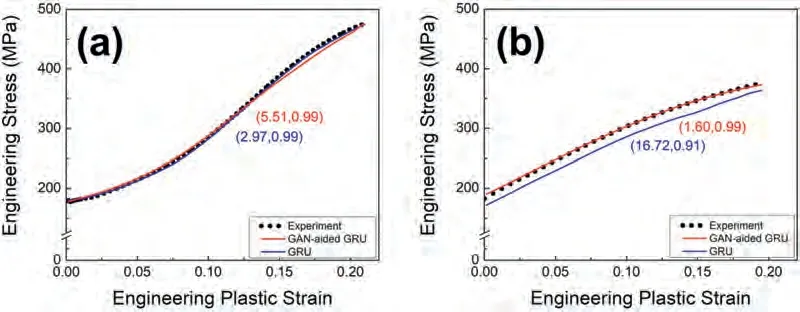
Fig.3.Predicted flow curves in the plastic regime compared with the experimental data obtained from (a) RD and (b) ND compressions.The test dataset corresponds to the interpolating condition (i.e.,annealed at 573 K for 1 h).The numbers in brackets indicate RMSE and R2.
Fig.4 compares the predictivity of the interpolating conditions with the 90 %-reduced training dataset.The predictivity of the RD flow curve was minimally modified by the GAN integration (Fig.4a).Both models provided precise RD predictions,with a significantR2of 0.99.However,they exhibited different predictive abilities for ND compression (Fig.4b).The GRU alone yielded an appreciable error in the ND estimation at plastic strain values higher than 0.12,as indicated by the arrows.RMSE increased from 9.61 to 14.3 MPa when focusing on the region of high plastic strain values.By contrast,the GAN-aided GRU exhibited a consistently precise estimation across the entire strains for ND curve,as characterized by RMSE of 6.65 MPa andR2of 0.99.These results correlate well with the interpolation using the original dataset,as aforementioned (Fig.3b).It is also noted that the 90 %-reduction in the dataset did not cause a significant deterioration in predictivity under the interpolating condition.The estimating errors remained limited to 12.6 and 12.8 MPa in the RD and ND compressions,respectively,based on the GAN-aided GRU model.The results indicate the remarkable performance of ML-based interpolation,even with a smallsized dataset.
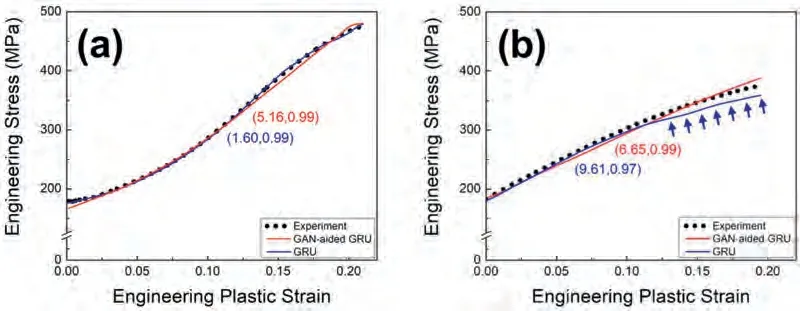
Fig.4.Predicted flow curves in the plastic regime compared with the experimental data obtained from (a) RD and (b) ND compressions.The test dataset corresponds to the interpolating condition (i.e.,annealed at 573 K for 1 h).The training dataset was reduced by 90 % from the original dataset.The numbers in brackets indicate RMSE and R2.The arrows in Fig.4b indicate the significant deviation made by the GRU alone.
Fig.5 shows the results of extrapolating prediction.In general,extrapolation is considered more challenging than interpolation because it estimates values beyond the experimental range.Moreover,extrapolation is more susceptible to errors than interpolation,particularly with a nonlinear relationship among the variables,or with a variation in the relationship out of the experimental range.However,no radical deterioration in predictivity was observed when the developed models were adopted for extrapolation.This satisfactory result could be attributed to the improved predictivity of the GRU algorithm with respect to extrapolation [41].For RD estimation,both approaches yielded similar results up to a plastic strain of approximately 0.09(Fig.5a).The GAN-aided GRU model exhibits a marginally larger error with increased strain.However,it significantly enhanced the predictability of the ND estimation (Fig.5b).It eliminated the large errors (up to 24.8 MPa)generated by the GRU alone in the 0–0.10 strain range,as indicated by the arrows.
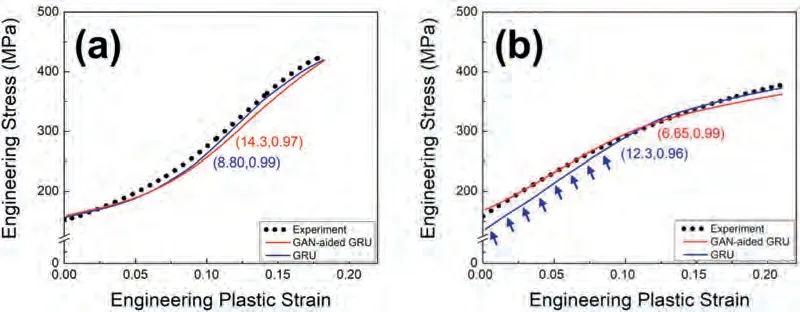
Fig.5.Predicted flow curves in the plastic regime compared with the experimental data obtained from (a) RD and (b) ND compressions.The test dataset corresponds to the extrapolating condition (i.e.,annealed at 673 K for 3 h).The numbers in brackets indicate RMSE and R2.The arrows in Fig.5b indicate the significant deviation made by the GRU alone.
Fig.6 shows the extrapolation results for the reduced training dataset.The predictivity was significantly degraded regardless of data augmentation,owing to the most extreme estimating conditions induced by the combination of data reduction and extrapolation.For RD prediction,the GAN-aided GRU model yielded an increased RMSE (14.2 MPa) and decreasedR2(0.97) compared with the GRU alone (8.49 MPa and 0.99,respectively) (Fig.6a).However,it is not conclusive whether data augmentation was ineffective.The GRU model presented unreasonable fluctuations for the RD prediction,as indicated by the arrows in Fig.6a.The GAN-based data augmentation removed these fluctuations and modified the flow curve to be reasonably smooth,with an error limited to 24.9 MPa,despite a slight increase in the RMSE.In this study,the developed model only failed to estimate the ND extrapolation of the 90 %-reduced training dataset (Fig.6b).These results are discussed in Section 5.3 with the SHAP analysis.Consequently,the GAN-aided GRU model developed in this study provided remarkable predictability for all the investigated conditions except for one.
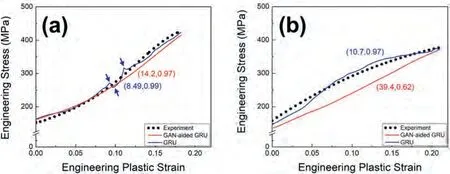
Fig.6.Predicted flow curves in the plastic regime compared with the experimental data obtained from (a) RD and (b) ND compressions.The test dataset corresponds to the extrapolating condition (i.e.,annealed at 673 K for 3 h).The training dataset was reduced by 90 % from the original dataset.The numbers in brackets indicate RMSE and R2.The arrows in Fig.6a indicate the unreasonable fluctuations made by the GRU alone.
5.Discussion
5.1. Anisotropic deformation behaviors induced by the caliber rolling
The distinct flow behaviors depicted in Fig.2 stem from the selective activation of deformation mechanisms depending on the loading direction.This topic has been comprehensively discussed elsewhere [7,22,23]with a microstructural characterization,given its broader scope beyond the present study.This subsection provides a concise summary of the underlying origins of anisotropic flow behaviors based on the authors’previous studies [7,22,23].
A caliber-rolled Mg alloy exhibits a unique basal texture in which the basal poles are split by approximately 30° from the ND to the TD on the cross-section [22].RD compression is perpendicular to most basal poles under such conditions,thereby resulting in the extensive activation of {10-12} extension twinning.This resulted in the formation of a concaveupward morphology of the RD flow curves in the early stage of deformation until extension twinning was depleted.Although TD compression induced a similar onset of {10-12}extension twins,the texture intensity was lower than that of RD compression because of the presence of basal poles against twinning (i.e.,poles close to the TD before compression).This resulted in the TD flow curves having lower curvatures than the RD flow curves.ND compression inhibited {10-12} extension twinning,as most basal poles were aligned with the compressive loading direction,whereas plastic deformation was primarily accommodated by basal slip.This was proven by three factors: (i) the highest Schmid factor for basal slip under the state,(ii) insufficient resolved shear stress for prismatic slip,and (iii) in-grain misorientation axis analysis,confirming that the majority of grains were deformed by basal slip [7].The inhibited {10-12}extension twinning results in a monotonic reduction in the strain-hardening rate of the ND flow curves,as shown in Fig.2c.
5.2. Superior performance of the developed approach
The GAN-aided GRU model successfully estimated the anisotropic flow curves under all conditions(Figs.3,4,5,and 6a),except for the ND extrapolation with a severely reduced training dataset (Fig.6b).Fig.7 depicts the parity plots of the various predictive approaches under interpolating conditions for further comparison.The GAN-aided GRU model provided the best predictivity and superior generalizability (i.e.,resistance to overfitting)among the analyzed approaches.This section explains the reasons for the superior performance of the GAN-aided GRU by comparing it to previous predictive approaches.

Fig.7.Predictions for(a)RD and(b)ND compressions using the GAN-aided GRU,GRU alone,previous ANN model[20],and constitutive equations[10].The numbers in brackets indicate RMSE and R2.
The previous ANN model [20]provided a good ND prediction with a low RMSE (3.28 MPa) and highR2(0.99),although both values were degraded for RD estimation(15.0 MPa and 0.98).This ANN model exploited hyperparameter optimization using the hyperband algorithm [38]and exhibited better predictivity compared to traditional ML methods,such as multiple linear regression and ANN without hyperparameter optimization [20].This finding supports the effectiveness of algorithm-based hyperparameter tuning,which is one of the four strategies involved in the proposed approach.
Another strategy explored in this study was the implementation of the RNN architecture (i.e.,GRU) known for its aptitude in handling sequential data.A few recent studies have investigated RNN’s applicability in predicting mechanical properties [42,43].For instance,LSTM model reduced RMSE by 68 %–80 % compared to the modified Johnson–Cook constitutive equation for estimating a high-temperature deformation behavior of Ni-base superalloy [42].However,these results do not assert the superiority of RNN over other ML approaches.Indeed,in a recent study [44],RNN performed less effectively than ANN in estimating the mechanical strengths of a metallic clad.The current results also corroborate the marginal improvement in predictive performance by substituting ANN with RNN,which is evident in both RMSE andR2.The GRU model enhanced the RD estimation compared to ANN,reducing the RMSE from 15.0 to 2.97 MPa.However,this improvement was attained at the expense of ND prediction with RMSE rising from 3.28 to 16.7 MPa.The imbalance in predictivity between the RD and ND remained unresolved in either case.This is clearly indicated by the deviation from the experimental results in their parity plots,i.e.,RD prediction by the ANN (Fig.7a) and ND prediction by the GRU (Fig.7b).In other words,both models exhibited insufficient generalizability,despite decent predictivity.
The GAN-based data augmentation strategy substantially bolstered the performance of the GAN-aided GRU model,enhancing both predictability and generalizability in comparison to the recurrent connections in the GRU.Expanding the size of the training dataset generally improves a model performance and reduces the expected variance,particularly in nonlinear cases[45].Accordingly,data augmentation has been actively explored to resolve the problem of limited datasets derived from a restricted number of experiments [46,47].The novelty of this study involves leveraging GAN for generating the synthetic flow curves.GAN and its variants have conventionally been utilized to generate synthetic images,rather than sequential mechanical data [48].The mechanical-data augmentation has relied on statistical measures instead.For example,Suh et al.[49]expanded the mechanical-property dataset of Mg alloys by incorporating averages and standard deviations.Although this method achieved favorable predictions under specific conditions,it is unsuitable for the present scenario where acquiring such statistical values is unfeasible.The current study successfully addresses this challenge by pioneering the application of GAN-based data augmentation.The proposed integration of GAN with GRU also sets it apart from a hybrid GAN-GRU model [50].The GRU architecture is implemented for the generator and discriminator of GAN in the hybrid model,whereas the GANaided GRU model innovatively leverages both architectures in parallel.
The constitutive equation is a conventional approach for interpreting the deformation behavior of a material.For the constitutive analysis of the ND estimation,this study adopted the power-law equation,which has been widely used for continuous hardening behavior and is expressed as follows:
where,σis the stress,εis the strain,nis the strain-hardening exponent,andKis a numerical constant.This model exhibited high accuracy with a low RMSE (4.23 MPa) and highR2(0.99),comparable to those of the previous ANN model (Fig.7b),suggesting that a constitutive approach can be as effective as the ML method in a specific case.However,this cannot be generalized to the RD and TD cases because Eq.(3) cannot describe a concave-upward curve because of its nature.
To attain the generalizability,Barnett et al.[10]introduced a constitutive framework incorporating multiple microstructural and mechanical parameters as follows:
where,Xis the volume fraction of grains favorable for{10-12} twinning,βindicates the extent to slip,fis the fraction of twinned area,σsis the slip stress,σTis the twinning stress,σ0tis the stress required to initiate twinning,σ0sis the stress measured when the basal axis was arranged perpendicular to the tensile direction,ξis the ratio of the stresses in the twinned and untwinned areas,Eis the elastic modulus,andεtis the strain caused by twinning.Although this equation provides valuable insights into the physical correlations among the parameters,it has several limitations in practical use.Some parameters (nandσ0s) should be determined from a separate experiment using a single crystal with an orientation unfavorable for {10-12} twinning.The other parameters were determined by assumptions (εt),numerical fitting (ξ),or manual adjustment (β).It should also be noted that this framework requires twinning kinetics (Xandf) with straining,which must be either frequently measured or assumed using another empirical equation.The lack of supplementary experiments resulted in poor predictability (Fig.7a).Other equations [11–15]have similar issues because of the inherent problems in the constitutive approach.The GAN-aided GRU,which combines the ML approach with data augmentation,can partially replace these methods because of its simpler,highly accurate,and generalized estimation with fewer experiments.
5.3. Extrapolation with the reduced training dataset
Upon revisiting Fig.6,the GRU model predicted unreasonable fluctuations,which were improved by integrating the GAN.Fig.8 depicts the estimations compared with the entire set of experimental data to clarify the reasons for the fluctuations.Notably,the RD compression predicted by GRU alone fell within the band composed of the experimental data obtained at 673 K,namely,the kernel training dataset (Fig.8a).Note that abrupt changes in the estimation,as indicated by the arrows in Fig.6a,were perfectly limited within this band.In other words,the model selected a relatively arbitrary value from this band instead of providing an effective prediction owing to the extreme estimating conditions (i.e.,extrapolation with the 90 %-reduced training dataset).The data augmentation with the GAN mitigated such severe prediction conditions by increasing the dataset size,thereby enhancing the predictive performance of the RD flow curve.Furthermore,this improved performance supports the conclusion that poor extrapolation can be attributed to the insufficient size of the training datasets.
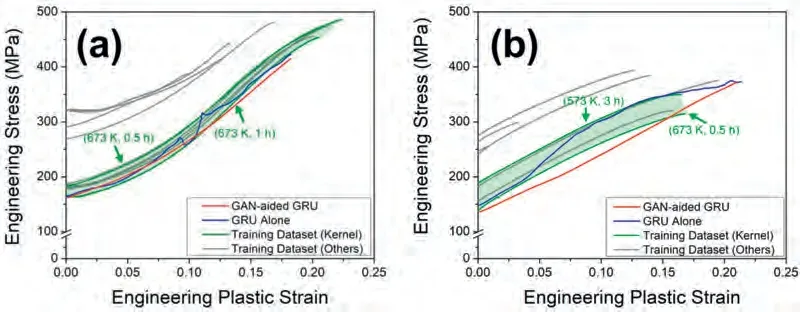
Fig.8.Extrapolating estimations using the 90 %-reduced training dataset shown with the entire experimental data for (a) RD and (b) ND compressions.The annealing conditions in the brackets indicate the kernel training datasets that constitute the band marked by green areas.
The ND flow curve predicted by the GRU alone was also within the band for which the boundaries were created by other flow curves (Fig.8b).In contrast to the RD estimates,neither of the proposed models provided an effective ND prediction.This difference stemmed from the significantly smaller size of the reduced ND training dataset (1982 instances) compared with the RD case (3593 instances).Such an inherent lack of ND dataset was hardly resolved even by integrating the GAN.These results led to two conclusions.First,integrating GAN with GRU can simultaneously improve predictability and generalizability.Second,a dataset threshold size exists for this improvement,below which the GAN becomes ineffective.
The extrapolated test dataset corresponded to the flow curve at 673 K for 3 h.The band for RD compression was formed by the flow curves obtained at 673 K for 0.5 h and 1 h (Fig.8a),whereas those for ND compression were defined by the curves at 673 K for 0.5 h and 573 K for 3 h,respectively (Fig.8b).This difference arose from the absence of ND data at 673 K for 1 h,as depicted in Fig.1.These results imply that the annealing temperature contributed more to the present estimations than the annealing duration.
SHAP provides deeper insights into the priority of features in a black-box ML model.Fig.9 presents the distribution of the SHAP values and their absolute averages with respect to the features.The mean absolute SHAP value of a given feature quantifies its contribution to the predicted output (i.e.,stress),whereas the colors represent the correlation direction(i.e.,positive or negative correlations).In the current prediction,the flow stress correlated with the input features in the following order: strain>temperature ≈direction>duration.Strain exhibited the highest contribution to stress,with a positive correlation,which was understood by the monotonic increase observed in most cases (Fig.2).The annealing temperature showed a negative correlation with the flow stress,although several unusual cases were confirmed,as indicated by the blue dots in the purple area.These unusual cases indicate a high stress after annealing at elevated temperatures owing to a beneficial loading direction,short annealing duration,or both.The loading direction and annealing duration presented an undefined order of feature tendencies,suggesting that the other features contributed more to the estimated flow stress.In particular,the SHAP-based contributions of the annealing temperature and duration are consistent with the above deductions.Therefore,the reduced extrapolation for RD compression was primarily governed by annealing temperatures,whereas that for ND compression was affected by both temperature and duration,owing to insufficient experiments along the ND at a temperature equal to the test dataset.
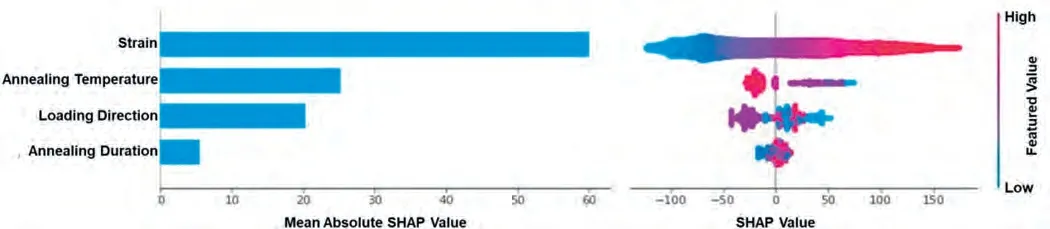
Fig.9.Contribution of each feature to the estimated flow stress based on the SHAP analysis: (a) mean absolute SHAP value and (b) distribution of SHAP values per feature.
5.4. GAN-aided GRU for material design
The developed model precisely predicted the plastic deformation behaviors within specific conditions of subsequent heat treatment while accounting for the significant plastic anisotropy.These factors exert a crucial effect on the mechanical properties of wrought Mg alloys.In specific,the investigated alloy exhibits considerable variations in mechanical properties (i.e.,up to 37 % decrease in tensile strength and 50 % increase in EL) in the processing window of 373–673 K and 10–360 min [23].The trade-off relationship between strength and ductility collapses at elevated temperature exceeding 473 K owing to alterations in microstructural mechanism [23].The plastic anisotropy is also ascribed to varying deformation mechanisms depending on the loading direction,as discussed in Section 5.1.Traditional models struggle to capture these intricate variations as it generally assumes static or linearly changing mechanisms,such as the constant YS-EL balance or homogeneous twin activation.On the other hand,the GAN-aided GRU can provide the enhanced predictability and generalizability due to the inherent strength of ML in handling the nonlinear correlations among various factors.
Finally,it is worth highlighting that the developed model can be easily implemented into finite-element analysis (FEA)to improve a material design due to the FEA-friendly characteristic of ML models [51].Researchers typically incorporate multiple constitutive equations to enable an FEA model to accommodate plastic anisotropy.For example,Trzepieci´nski and Gelgele [52]utilized three constitutive equations along RD,TD,and 45° to RD,respectively,to simulate the FEA of a rectangular deep drawing.Similarly,Kim et al.[53]employed two constitutive equations to model a three-point bending of Mg sheet.The proposed approach is expected not only to streamline the experimentation process but also to simplify the mechanical modeling in FEA by adopting the unified ML-based equation adaptable to various loading conditions.A notable illustration of this capability is seen in the work of Zhao et al.[54]where FEA was employed to analyze a metal-rubber isolator using mechanical properties predicted by ANN subroutine.This simulation not only estimated an elastic modulus of raw material,but also precisely predicted the shock response of the metal-rubber isolator with a complex design.
6.Conclusions
The current study represents the first application of ML techniques,besides the simple ANN,to accurately predict the severe anisotropy of compressive deformation behaviors for the wrought Mg alloys.The unique split texture formed by caliber rolling and subsequent annealing resulted in different compressive deformation behaviors depending on the loading direction.The GAN-aided GRU model demonstrated the remarkable predictivity in most scenarios,irrespective of the estimation type (i.e.,interpolation and extrapolation)and dataset size.It only failed to the ND extrapolation with a 90 %-reduced training dataset owing to acute data limitations.Furthermore,the developed model exhibited the improved generalizability compared to the previous DNN model or GRU alone.The superior predictive performance is ascribed to hyperparameter optimization,GAN-based data augmentation,and the intrinsic extrapolation capability of the GRU architecture.In particular,GAN-based data augmentation plays a profound role in enhancing the model performance.SHAP analysis clarified the higher priority of the annealing temperature than that of the duration,which explained the different kernel datasets between the RD and ND compressions.The developed model is a promising alternative to traditional constitutive approaches with the limitations of numerous assumptions,numerical fittings,and manual adjustments.The implementation of GAN-aided GRU into FEA is expected to enhance the structural design of Mg components.Overall,this study offers a novel perspective for predicting the anisotropic deformation behavior of wrought Mg alloys exploiting ML techniques with data augmentation.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
CRediT authorship contribution statement
Sujeong Byun:Conceptualization,Software,Validation,Visualization,Writing– original draft,Writing– review &editing.Jinyeong Yu:Investigation,Methodology,Validation,Writing– review &editing.Seho Cheon:Data curation,Methodology,Writing– review &editing.Seong Ho Lee:Data curation,Methodology,Writing– review &editing.Sung Hyuk Park:Data curation,Resources,Writing–review&editing,Conceptualization.Taekyung Lee:Conceptualization,Methodology,Project administration,Resources,Software,Supervision,Validation,Visualization,Writing–original draft,Writing– review &editing.
Acknowledgment
This work was supported by Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (Grant No.20214000000140,Graduate School of Convergence for Clean Energy Integrated Power Generation),by Korea Basic Science Institute (National Research Facilities and Equipment Center)grant funded by the Ministry of Education (2021R1A6C101A449),and by the National Research Foundation of Korea grant funded by the Ministry of Science and ICT (2021R1A2C1095139),Republic of Korea.
 Journal of Magnesium and Alloys2024年1期
Journal of Magnesium and Alloys2024年1期
- Journal of Magnesium and Alloys的其它文章
- A comprehensive review on the processing-property relationships of laser strengthened magnesium
- Recent advances in electrochemical performance of Mg-based electrochemical energy storage materials in supercapacitors: Enhancement and mechanism
- Peri-implant gas accumulation in response to magnesium-based musculoskeletal biomaterials: Reframing current evidence for preclinical research and clinical evaluation
- Influence of laser parameters on the microstructures and surface properties in laser surface modification of biomedical magnesium alloys
- Experimental and simulation research on hollow AZ31 magnesium alloy three-channel joint by hot extrusion forming with sand mandrel
- Mg/MgO interfaces as efficient hydrogen evolution cathodes causing accelerated corrosion of additive manufactured Mg alloys: A DFT analysis
