初中数学二次函数动点问题解题方法

郭香

【摘 要】  随着初中数学教学的进程，结合动点问题的二次函数已成为竞赛、中考的核心内容.这类问题强调了函数、动点与其他数学知识的综合运用，展示了初中数学的实际应用价值与其综合性.由于动点问题的求解需要特定的数学技巧和深厚的基础，对此有必要进行系统的研究和探讨.本文通过对二次函数题型的分析，对与动点相关的题型及其解题方法进行了详尽的研究，旨在提供全面的方法论参考，以增强学生的解题能力和优化教学方法.

【关键词】  二次函数；动点问题；题型特点；解题方法

动点与二次函数结合常涉及点的运动路径与其他几何图形或直线的关系，需要学生不仅掌握函数的基本性质，还要灵活运用几何和代数的知识.为此，本文深入探讨几种二次函数的题型，并提出相应的解题策略.希望为教育工作者和学生提供清晰、系统的指导.

1 动点与直线相结合

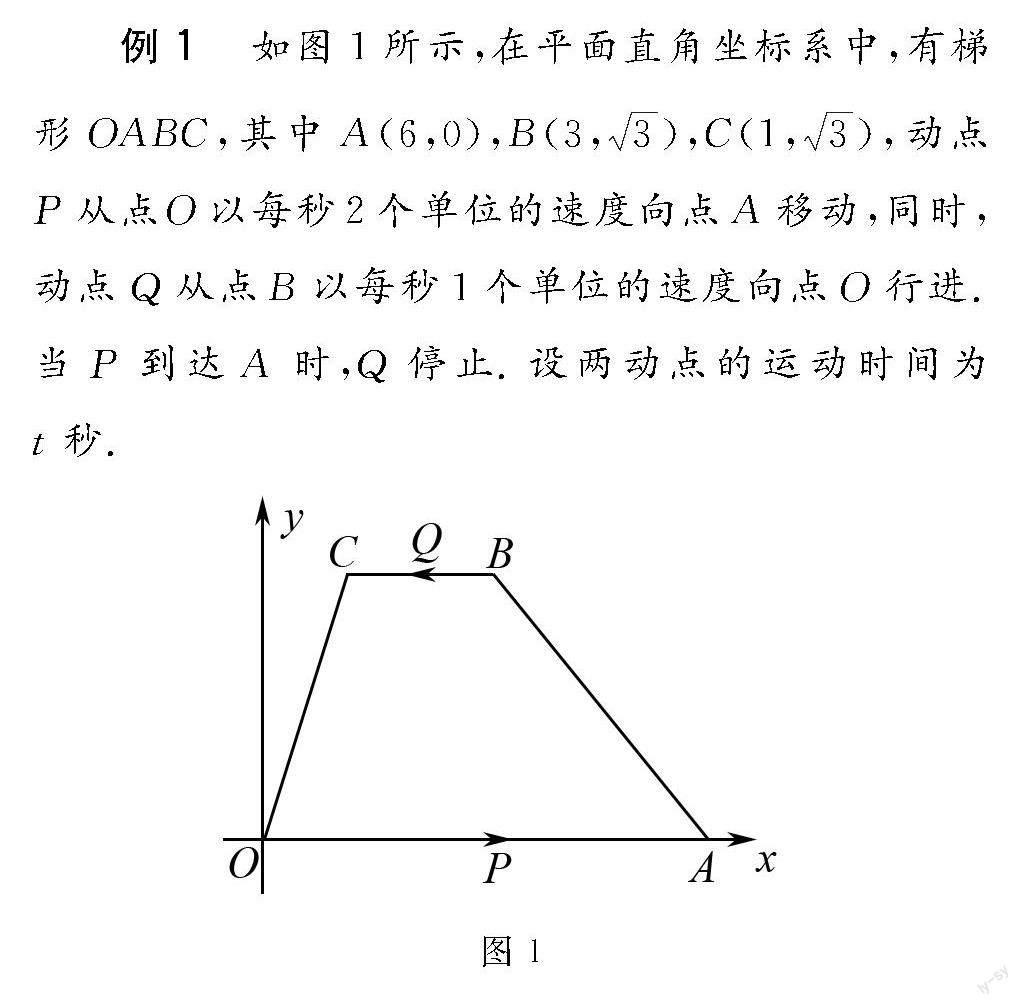
例1  在平面直角坐标系中，有梯形，其中，动点P从以每秒2个单位的速度向A移动，同时，动点Q从点B以每秒1个单位的速度向点O行进.当P到达A时，Q停止.设两动点的运动时间为t秒.

图1 例题图1

（1）求经A、B、C的抛物线方程；

（2）若Q在CO上移动，找出面积S与时间t的关系；

（3）判断以O、P、Q为顶点的三角形是否为直角三角形，并给出t值或原因；

（4）判断经A、B、C的抛物线的对称轴、直线OB和PQ是否交于一点，并给出t值（或范围）或原因.

分析  解题首先需要将动态转化为静态，也就是将动点在某一时间t的状态“固定”下来，从而分析其轨迹，并确定其坐标及变量的取值范围.根据题目所要求的结论，可以运用逆向思维的方法进行探讨.例如，要证明三条线是否交于一点，可以先确定其中两条线的表达式，进而求出它们的交点.将这一交点代入第三条线的方程中，检查其是否满足方程的条件.如满足，即可证明三线交于一点；反之，则证明三线不交于一点.

对于第（4）问，抛物线的对称轴可以由A、B、C三点求得.得到对称轴后，可以求直线OB的方程.设这三条线交于点M.利用抛物线的对称性和直线OB，确定M的坐标.由于P、Q都是动点，通过已知的M和动点P，列出PM的方程.最后，考虑Q的运动情况，代入坐标来验证题目的条件.

2  动点与几何图形相结合

例2  在平面直角坐标系中，抛物线分别与x轴交于点A、B，与y轴交于点C.D是C关于x轴的对称点，P是x轴上的动点，坐标为（m，0）.由P引垂线l与抛物线相交于点Q.

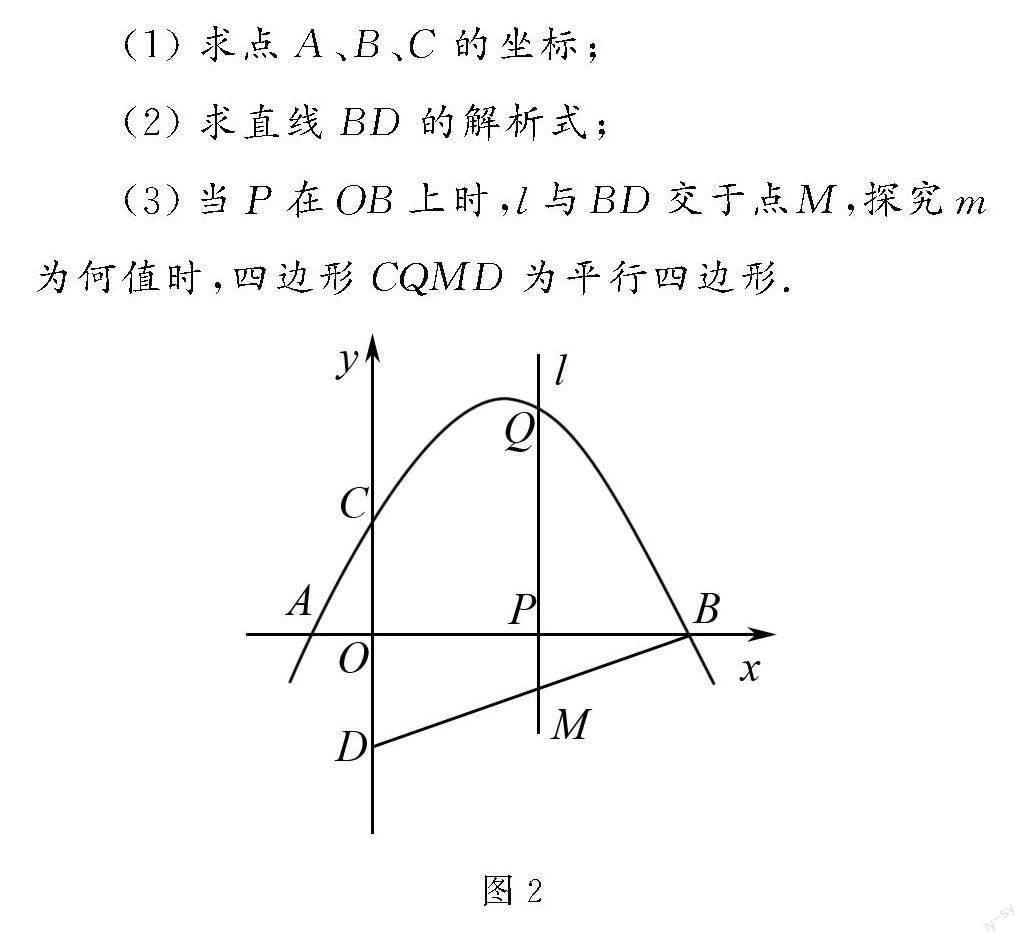
图2 例题图2

（1）求点A，点B，点C的坐标；

（2）求直线BD的解析式；

（3）当P在OB上时，l与BD交于点M，探究m的值使CQMD成为平行四边形；

分析  从静态出发，固定动态的某一状态，明确动点P的坐标为（m，0）后，先解二次方程求出与x轴、y轴交点的坐标，确定A、B、C三点的确切位置.接着，通过点C和x轴的关系，可以轻松确定点D的坐标，并据此得到直线BD的解析式.但解题的关键在于动态与静态的结合[1].当点P在线段OB上运动时，需要确定直线l与直线BD的交点M.这里，学生需要用直线与抛物线的交点公式，结合平行四边形的性质来求解.确定m的取值范围后，便是分析三角形的性质.利用勾股定理，将三边表示为变量，从而判断是否能构成直角三角形，并据此确定Q点的坐标.

3  动点与分类讨论相结合

例3  在四边形OABC中，轴于C，A（1，-1），B（3，-1）.动点P从O出发，沿x轴正方向以2单位/秒速度行进，引PQ⊥OA交于Q.若P点移动时间为t秒，与四边形OABC重叠的面积记作S.

（1）求经O、A、B的抛物线方程并确定顶点M；

（2）用t表示P、Q坐标；

（3）将绕P点逆时针旋转90°，探究是否存在某t使O或Q落在抛物线上，并给出t或理由；

（4）求S关于t的函数.

分析  此题实质是考查学生在动态与静态、几何与代数之间的转换能力，以及对各种几何关系和性质的掌握.基于动点P的运动轨迹，可以确定其在不同时间下的坐标，再据此推导出与P相关的点Q的位置.然后，结合題目所给的几何关系和性质，分析点P和Q的变化如何影响整个四边形OABC或其中的部分形状[2].

对于第（3）问，根据动点P的位置和与之相关的点Q的旋转，分析出O点和Q点与抛物线的位置关系.考虑的旋转后的形状和位置，以及与抛物线的交点情况，从而进行分类讨论.

第（4）问，要研究的是与四边形OABC的重叠面积S与时间t的关系.分析动点P在不同位置时，与四边形OABC的位置和形状关系，以及重叠情况.根据不同的情况，推导出S与t的关系式.

3  结语

综上所述，二次函数的动点问题不仅考验学生的数学基础，更考验其解题技巧.通过对这一题型的深入研究，学生得以更为清晰地理解其特点与挑战，从而找到有效的解题方法.本文的分析与探讨为教育者和学生提供了有价值的参考，期望能够推动初中数学教学的进一步优化.

参考文献：

[1]涂晨.有关初中数学课后习题选配的几点思考——以人教版“二次函数的概念”为例[J].内蒙古师范大学学报（教育科学版），2022，35（02）：136-140.

[2]王茜，林磊.初中数学章起始课教学案例研究——以“二次函数”章起始课教学为例[J].榆林学院学报，2022，32（02）：91-95.