截止节流阀两相流致噪声特性分析

王旭飞，王均宇，戴磊，宋永兴，，于跃平

(1.山东海筑暖通工程有限公司，山东济南 250014；2.山东建筑大学热能工程学院，山东济南 250101；3.压缩机技术国家重点实验室(压缩机技术安徽省实验室)，合肥安徽 230031)

0 前言

节流阀是通过改变节流截面或是节流长度来控制节流流体，在空调中节流阀起到节流降压的作用[1-3]。当具有一定压力势能的流体流到节流阀时，节流面收缩，部分压力势能转变为动能使得流体流速增大；同时压力降低，当压力降低到制冷剂的饱和蒸汽压力时便会产生空泡[4-6]。空泡随流体流动，空泡流出阀门下游，局部压力略有增大，气泡破裂从而形成空化[7-9]。而气泡之间相互碰撞、空泡坍塌等形成空化噪声，这也是节流阀流致噪声的来源之一[10-11]。另外，流体流动不稳定使得流场出现紊流、回流、漩涡等，造成流体动力噪声增大，这是阀门噪声的另一来源之一。在空调系统中，节流阀是重要组成元件之一，同时也是空调噪声的来源之一，故而成为学者们研究的对象。

黄皓[12]通过对不同工况下的电子膨胀阀进行数值计算，发现阀门开度和压差是影响阀门下游噪声的重要因素。ZHANG等[13]通过对不同背压下的锥形电子膨胀阀进行数值计算，发现制冷工况下噪声主要出现在下游区域，且流场中的最大噪声值以及剖面上各个噪声源的强度都随入口压力的增大而增大。王世鹏[14]通过数值计算分析了调节阀内在不同开度和不同出口压力下的流体流动和空化现象，结果发现空化主要出现在阀门出口端的拐角和阀芯窗口。陈修高等[15]通过数值计算对不同进出口压差下的调节阀进行研究，结果发现空化噪声是调节阀噪声的主要来源，且随阀门进出口压差的增大而增大。ARIYADI等[16]使用CFD模拟对电磁阀内部产生的流动特性和空气动力学噪声进行了数值研究，研究结果表明：不同的入口条件会影响局部速度，从而导致不同量级的湍流强度，通过修改出口通道处的流动路径可将空气动力学噪声降低2%～12%。ZHANG等[17]通过实验和仿真方法研究不同开度和进口压力下调节阀的流场分布，并利用在阀芯加沟槽的方式实现了降噪。HAN等[18]分析了提升阀背压对流动特性、空化和流动力的影响，并采用两相混合模型进行计算，结果表明：最大速度随着压降的增加而迅速增加从而导致阀门内部出现更严重的气穴现象。

传统节流元件如毛细管等虽然成本低，但是在工作过程经常出现堵塞、流量受限等问题[19-20]。随着空调技术的发展，新型电子膨胀阀、截止节流阀等逐渐代替毛细管的应用，但在应用过程中同样伴随着空化及噪声的产生。本文作者以截止节流阀为研究对象，通过数值计算对不同入口流量下的截止节流阀进行研究，通过对其内部流场进行分析为其优化降噪提供方向。

1 截止节流阀模型

1.1 物理模型

以某厂家的截止节流阀为研究对象，图1所示是该模型的剖面示意。

图1 截止节流阀模型

截止节流阀主要由固定式阀座、活动式阀芯、两个过滤网组成。作者对制冷工况下的流场进行计算，以R410A制冷剂为介质进行研究。图示制冷剂流向为制冷时的流动方向，当制冷剂左进下出时，活动式阀芯被流体冲击移动到固定式阀座位置，此时阀门处于制冷状态。对该模型进行反向建模得到计算流体域，考虑到阀门实际安装方向和管路连接方式，最终得到的计算流体域如图2所示。

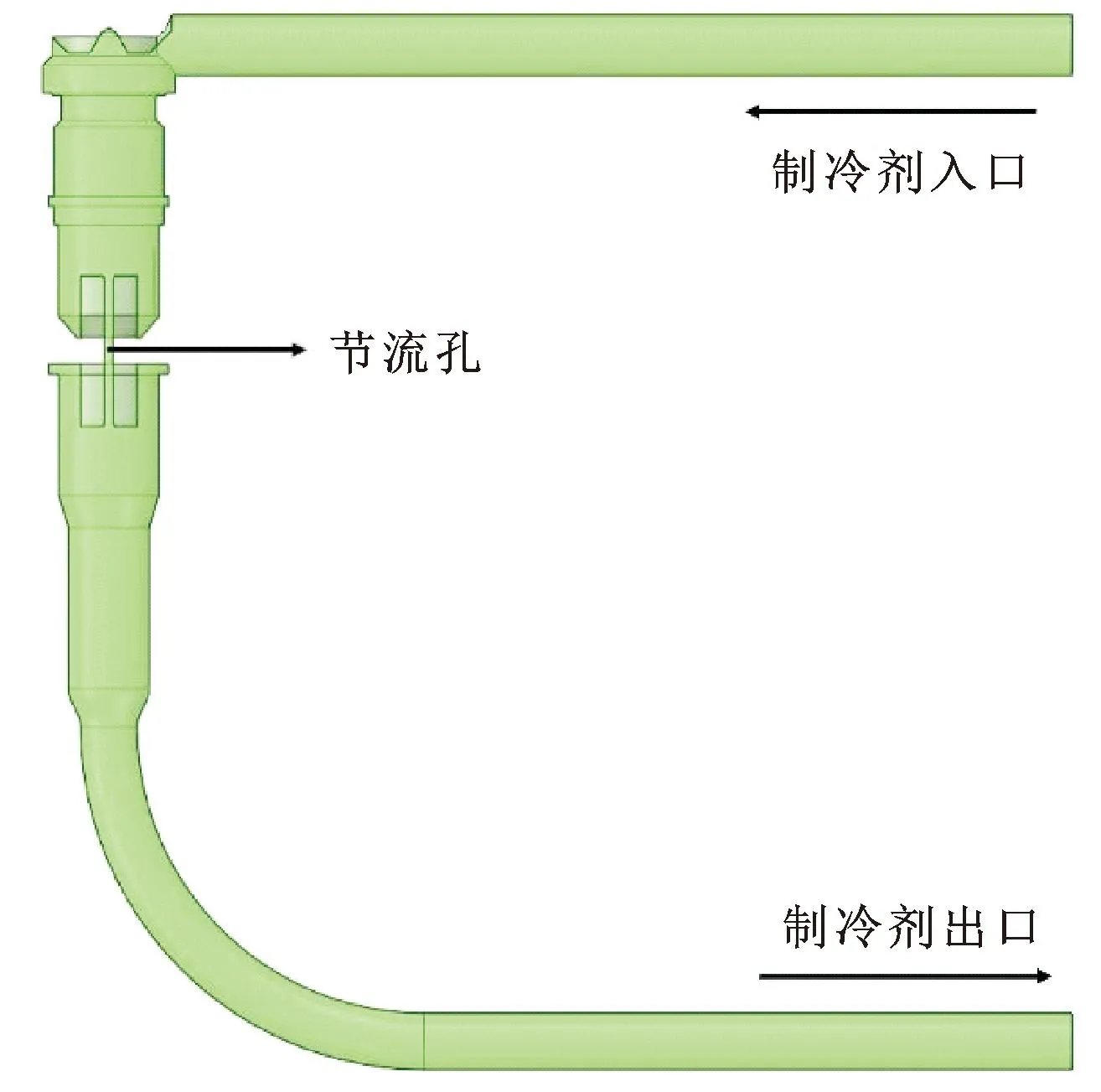
图2 截止节流阀计算流体域

1.2 数学模型

以R410A制冷剂为介质进行研究，设置边界条件为流量入口和压力出口，分别对入口流量为0.014、0.016、0.018、0.020、0.022、0.024 kg/s、出口压力为1.498 MPa工况下的阀门进行数值计算。由于阀门内部流动较为复杂，属于高雷诺数的湍流流动，因此选择Realizableκ-ε湍流模型进行计算。在制冷剂流动过程中，由于阀门节流降压作用，使得阀门出口呈两相流流出，而制冷剂流致噪声又属于宽频噪声，因此选择Zwart-Gerber-Belamri空化模型、VOF多相流模型和Broadband Noise Sources噪声模型进行计算。具体控制方程如下所示：

质量守恒方程：

(1)

能量守恒方程：

(2)

动量守恒方程：

(3)

(4)

(5)

式中：u、v、w是流体速度在x、y、z三个方向的分量，m/s；ρ是流体密度，kg/m3；cp为定压比热容，J/(kg·K)；T为温度，K；k为流体的传热系数，W/(m·K)；v是来流的速度矢量，m/s；ST为流体的内热源及由黏性作用流体机械能的部分；Fbx、Fby、Fbz是单位流体上的质量力在x、y、z方向上的分量，N；pxx、pyx等是流体内应力张量的分量，N。

Broadband Noise Sources噪声模型：

(6)

(7)

(8)

式中：U为湍流速度，m/s；l为湍流特征长度，m；α0为声速，m/s；α为模型常数；Mt为湍流马赫数；n为湍动能，m2/s2；PA为声功率，W/m3。

Zwart-Gerber-Belamri空化模型：

(9)

(10)

式中：pv为液体在相应温度下的饱和蒸汽压力，Pa；αv为气相体积分数；RB为空泡半径，m；ρ为混合相密度，kg/m3；ρ1为液体密度，kg/m3；ρv为气体密度，kg/m3；Re为蒸发相生成率；Rc为凝结相生成率。

2 网格无关性分析

在对截止节流阀内部流场进行分析时，首先要对其进行网格划分。网格数量影响计算速度，而网格质量决定计算的准确性，因而网格数量和质量是决定计算速度和结果准确性的关键因素。图3所示是阀门监测点示意，当以一定质量流量流入阀门时，通过与出口监测点监测到的流量进行对比来确定计算误差是否满足计算要求。

图3 截止节流阀监测点示意

由于阀门上下游结构较为简单，而节流孔区域结构复杂且面积较小，因而对图示节流区域进行加密处理。图4所示是用不同网格尺寸进行加密得到的4种数量的网格模型。以0.02 kg/s的质量流量作为入口边界条件，以相同压力作为出口边界条件分别进行计算，当计算收敛后对出口监测点的流量与所设定的入口流量进行对比，结果如图5所示。可以看出：随着网格数量逐渐增多，阀门出口的流量逐渐接近设定的入口流量值，且进出口误差也随网格数量的增大而减小；但当网格数量增大到一定程度时，对计算误差的影响减弱，同时网格数量的增多也会使计算速度减慢。考虑到网格数量对计算效率和计算准确性的影响，选择65.005 0×104数量的网格进行计算。

图4 节流孔加密网格示意

图5 网格无关性验证

3 仿真结果分析

基于CFD对截止节流阀进行研究，通过对入口流量分别为0.014、0.016、0.018、0.020、0.022、0.024 kg/s和相同压力出口为边界条件的工况进行计算，最终得到其速度场、涡量场、压力场、气相体积分数以及声功率级等特性。

3.1 速度场及涡量特性分析

当制冷剂以一定的流量流入阀门时，在节流前流体的流速较小，而在节流后由于阀门的节流降压作用使得节流孔处流速突增。图6所示是在6种入口流量下的速度场，可以看出：当流体流到节流孔时，流向的突变使得节流孔中心流速较大，而在贴近节流孔壁面上，由于流体的黏性力等使得壁面处的流速较小；随着阀门入口流量的增大，阀门节流孔处的最大速度从44.331 3 m/s增大到77.560 4 m/s，且在阀门下游流速呈喷射状分布。

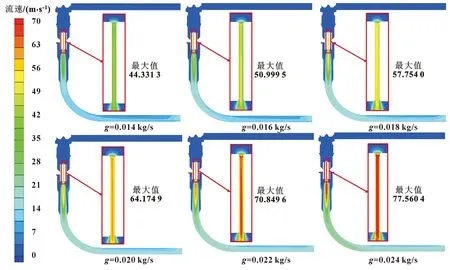
图6 不同入口流量下速度场分布

阀门节流前管道结构简单，流体流动较为稳定，而在节流时流道的突变是引起流动不稳定的因素之一。图7所示是6种工况下的涡量分布。可以看出：涡量主要集中在阀门下游，而最大涡量产生在节流孔区域。在流体流到节流孔时，由于横截面的减小使得流体流速增大，而在靠近节流孔壁面处流速较小，从而形成较大的速度梯度，从而在剪切力的作用下引起流动的不稳定。当流体流出时，阀门下游流道横截面突增，使得具有较大动能的流体以喷射的形式流出，而在速度梯度等的作用下也会与下游流体形成剪切力，因而形成较大的旋涡且呈对称态分布在阀门下游管道区域。

图7 不同流量下涡量分布

3.2 压力场及气相体积分数分布

单相制冷剂以液态的形式流入截止节流阀，在节流降压后以气液两相流流出。图8所示是在不同入口流量下的压力场分布，可以看出：压降主要出现在节流孔位置。当流体流经阀门节流孔时，恒定入口流量下由于管径的突缩使得流体流速增大，动能增加。根据能量守恒定律可知，能量不会无缘无故消失也不会突然出现。当动能增加时，相应的压力势能减小，这也就是截止节流阀的节流降压原理。从图8可以看出：随着阀门入口流量的增大，节流孔处的压降也逐渐增大，且在节流孔入口贴近壁面的拐角处出现压力极小值。这是由于流体流向突然改变时，左右两个方向的流体发生相互作用的抵消力而产生的。当压力小到一定程度时，便会产生气液两相流。

图8 不同流量下压力场分布

图9所示是不同入口压力下的气相体积分数分布，可以看出：节流前制冷剂以单相流流动，经过阀门节流降压作用后下游呈气液两相流流动。当高温高压制冷剂以一定的流速流动时，在阀门节流孔处出现压降，当压力降低到该工况制冷剂的饱和蒸汽压力时，便会产生空泡，由于节流孔的流速较大，气泡不易堆积，因而空泡随流体流到阀门下游形成空化。由于阀门设定的出口压力小于制冷剂的饱和蒸汽压力，因而下游空化相对严重。而在节流孔入口贴近壁面的拐角位置只有少量的空泡堆积。

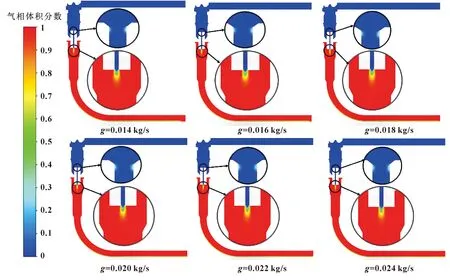
图9 不同流量下气相体积分数分布

3.3 声功率级分布

当制冷剂流入节流孔时，部分压力势能转变为动能，由于节流孔的结构较为复杂，压力势能会有损耗从而转变为声能，同时声能又以辐射的形式表现出来形成噪声。图10所示是不同流量下的噪声分布，局部区域是节流孔入口的噪声分布。可以看出：噪声是从节流孔入口开始产生的。当一定流速的流体流到节流孔时，由于管道横截面减小，管束收缩，节流孔两侧的流体产生相互作用的力，两者相互抵消从而产生噪声。当制冷剂流量逐渐增大时，流体流速增大，同时节流孔入口处噪声也随之增大。

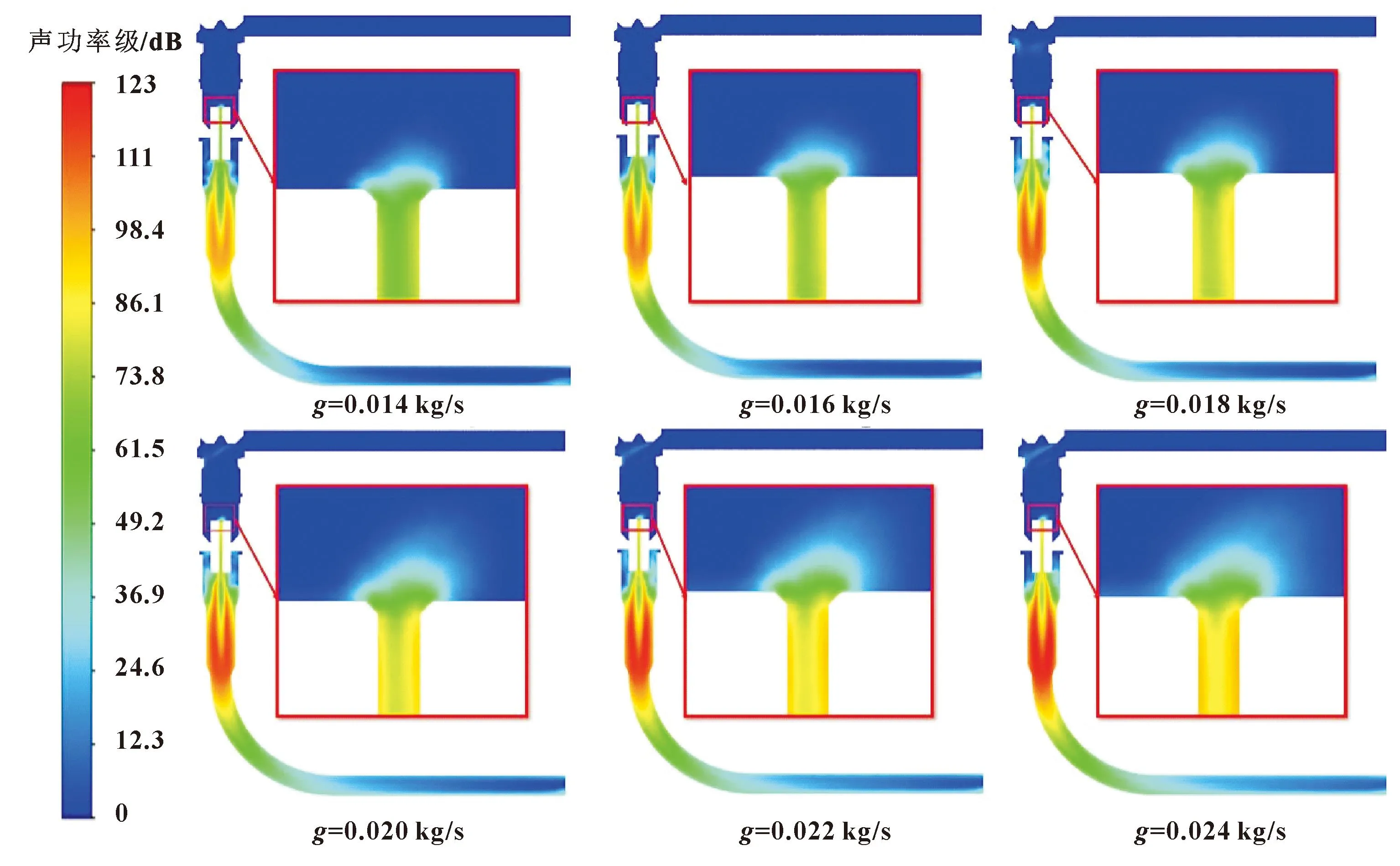
图10 不同流量下噪声分布

制冷剂以液体流入截止节流阀，经过阀门节流降压作用后以两相流流出，因而在流体流动过程中除了流体动力噪声外也伴随着空化噪声的产生。图11所示是不同入口流量下阀门上下游声功率级的分布。可以看出：噪声主要产生在阀门下游，在节流上游拐角位置也有少量噪声产生，这是由流体流向发生改变时流体相互碰撞和流体碰撞阀门产生的。制冷剂在节流孔处由于阀门节流作用而使局部压力减小，当减小到制冷剂饱和蒸汽压力时就会产生空泡，空泡随流体流动到下游，空泡之间相互碰撞产生空化噪声。另一方面，由节流孔射流而出的流体与管壁碰撞，并与贴近壁面处流体形成势差从而形成漩涡，产生较大的流体动力噪声，因而阀门下游噪声较大。从图11可以看出：随着阀门入口流量的增大，阀门下游最大噪声从104.640 2 dB增大到122.751 5 dB。

图11 不同流量下阀门上下游声功率级分布

图12所示分别是流体域Y方向上的坐标以及A-A剖线上的噪声源分布。从图(b)可以看出：节流区域前有少量噪声产生，从节流孔入口开始噪声突增，之后略有减小而后又逐渐增大到最大值再减小。由于流体流束收缩使得流体相互碰撞，因而在节流孔入口出现噪声突增至极大值的现象。在节流孔区域流动逐渐稳定，由流体流动不稳定的作用减弱，因而噪声略有减小。当流体流出节流孔至下游区域，流体动力噪声与空化噪声同时产生，因此出现噪声增大的现象，且该区域引起噪声增大的因素较多，因而伴随着阀门最大噪声的出现。当流体流到下游弯管区域时，流体射流不再明显，由速度梯度引起的涡流及回流等现象减弱，流体动力噪声随之减小，因而弯管处噪声逐渐减小。虽然不同流量下该剖线上的噪声分布趋势相同，但各点噪声源的强度都随着流量的增大而增大。

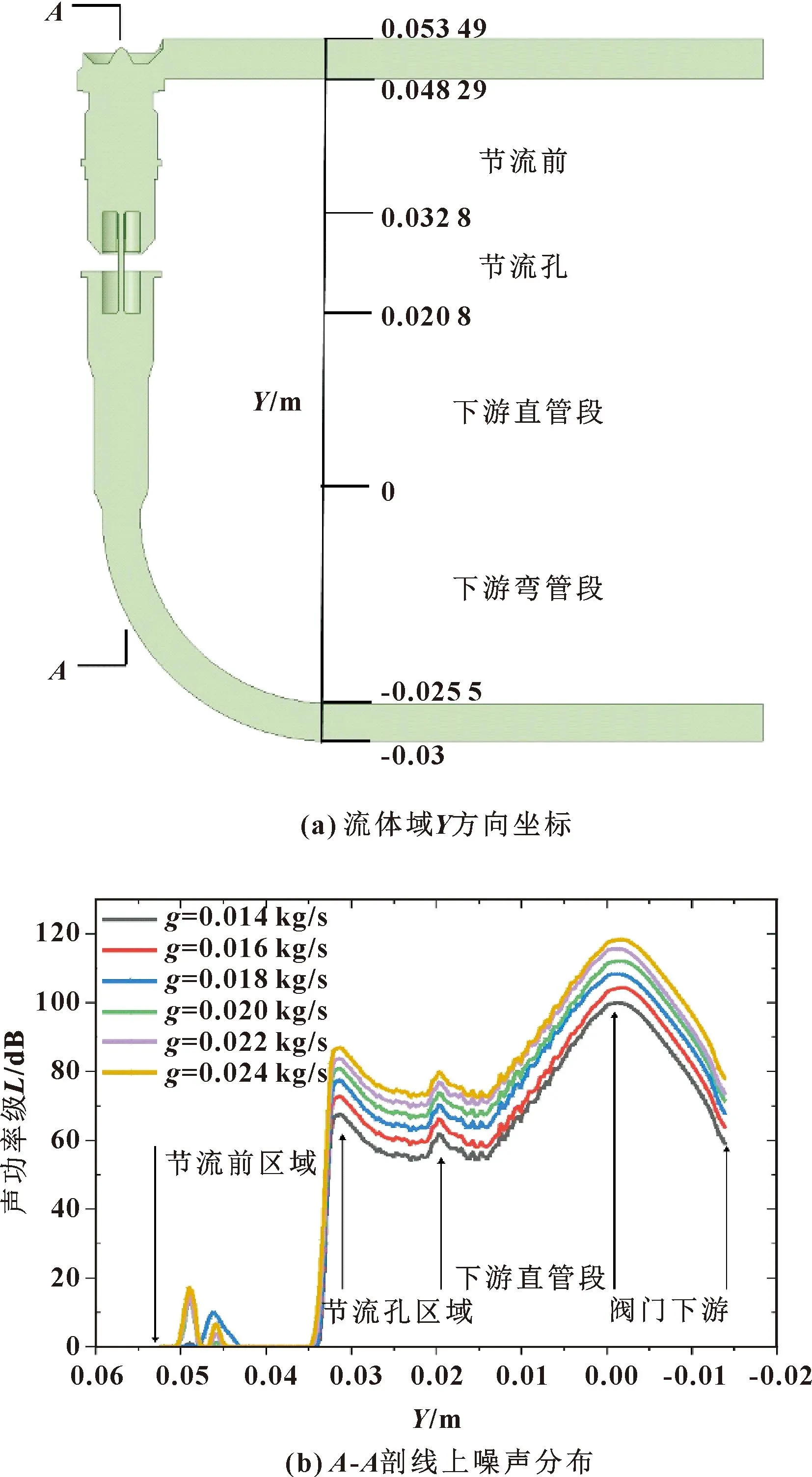
图12 Y方向剖线上噪声源分布

4 结论

通过数值计算对不同入口流量下的流场进行计算，并对其速度场、涡量场、压力场、气相体积分数分布以及噪声等进行分析，最终得出以下结论：

(1)随着阀门入口流量的增大，流场中最大流速也随之增大。阀门节流孔处的最大流速从g=0.014 kg/s时的44.331 3 m/s增大到g=0.024 kg/s时的77.560 4 m/s，且在阀门下游流速呈喷射状分布。

(2)随着阀门入口流量的增大，节流孔处的压降也逐渐增大，且在节流孔入口贴近壁面的拐角处出现压力极小值。

(3)节流前制冷剂以单相流流动，经过阀门节流降压作用后下游呈气液两相流流动。由于阀门设定的出口压力小于制冷剂的饱和蒸汽压力，因而下游空化相对严重。而在节流孔入口贴近壁面的拐角位置只有少量的空泡堆积。

(4)随着阀门入口流量的增大，阀门下游最大噪声从104.640 2 dB增大到122.751 5 dB。节流区域前有少量噪声产生，从节流孔入口开始噪声突增，之后略有减小而后又逐渐增大到最大值再减小。虽然不同流量下阀门中心线上的噪声分布趋势相同，但各点噪声源的强度都随着流量的增大而增大。

(5)在制冷工况下，噪声主要集中在节流孔以及阀门下游，在之后的优化设计中可以针对这两部分的流场流线对阀门结构进行改造以达到降噪的目的。