新型缓冲结构的直线气缸动力学分析与试验研究

钟隆峰，杜群贵

(华南理工大学机械与汽车工程学院，广东广州 510640)

0 前言

现阶段，气动系统中关键元件气缸，被广泛用于各种自动化生产设备中[1- 2]。然而，高速气缸工作过程中无法避免其行程末端的缓冲问题。目前高速气缸缓冲方式主要有内置溢流阀缓冲和外置回路缓冲，内置式缓冲方式由于其结构简单、安装方便且易于更换，有利于节约成本，因此被广泛用于现有的高速气缸产品上。

在缓冲气缸的建模仿真方面，文献[3]对一般的气缸运动过程进行了仿真分析。而针对溢流式缓冲结构，文献[4]建立了动力学模型，分析了溢流阀结构参数对其缓冲性能的影响。在新型结构研究方面，文献[5]提出一种组合阀门式新型缓冲结构，并对其性能进行分析。然而现在新兴的电磁缓冲结构被广泛应用于火炮后座、车架悬座等领域[6]，尚未应用于气缸的缓冲领域。

基于以上原因，本文作者提出一种新型电磁缓冲结构，并通过电磁学理论建立了该缓冲结构的动力学模型，结合气缸工作原理，利用热力学等理论建立新型缓冲结构的直线气缸动力学计算模型，通过试验验证理论计算模型的正确性。并对比分析了溢流阀缓冲、新型电磁缓冲以及两者共同存在时的缓冲效果。

1 新型缓冲结构的建模与分析

研究采用的新型缓冲结构的直线气缸结构如图1所示，其中新型缓冲结构Ⅳ包括动子9、硅钢片10及线圈11。在气缸运行过程中，活塞杆带动动子进入缓冲行程时，动子上的永磁体产生的磁场通过硅钢片产生回路，进而与线圈相互作用，以一定速度切割磁感线，在线圈中产生电流，因而与永磁体相互作用产生电磁阻力。

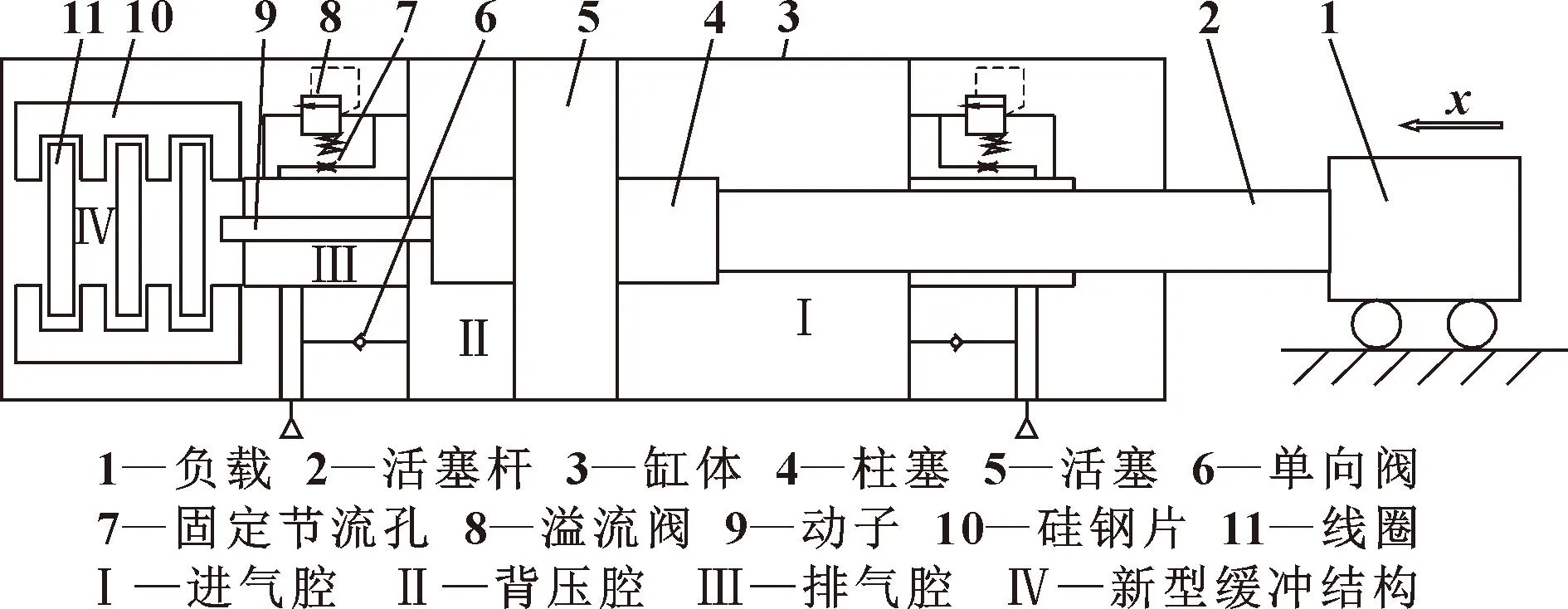
图1 新型缓冲结构的直线气缸结构

针对新型电磁缓冲结构，本文作者首先采用电磁学理论建立磁场分布模型以及电磁力模型。

1.1 磁场分析

新型电磁缓冲结构如图2所示，其中包括定子铁芯、线圈、动子铁芯和永磁体。铁芯一般为硅钢片高导磁材料，而永磁体为轴向充磁的圆环形永磁体，且沿x轴方向周期性分布，交替更换极性方向，在气隙间产生磁场。图中：Rr为动子铁芯外半径；Rm为动子永磁体外半径；Ri为定子线圈内半径；Rs为定子铁芯内半径；hm为永磁体径向厚度；g为气隙长度；τp为永磁体极距；τm为永磁体轴向长度；τs为槽宽；τt为槽距。

图2 新型电磁缓冲结构示意

对于新型电磁缓冲结构而言，矢量磁位与周向位置θ无关，且在气隙区域满足拉普拉斯方程[7]，满足∇2F(x，y)=0，即：

(1)

解上式微分方程可得磁场分布为

(2)

且满足

(3)

(4)

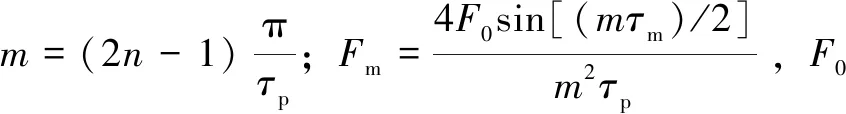
需要指出的是，由电磁理论可知永磁体与线圈相互切割磁感线只与径向分量有关，而与轴向分量无关，因此只求解磁场的y方向分量。磁场分布求解结果如图3所示。由图3(a)可以看出：解析计算与有限元分析结果误差较小，变化规律非常一致。

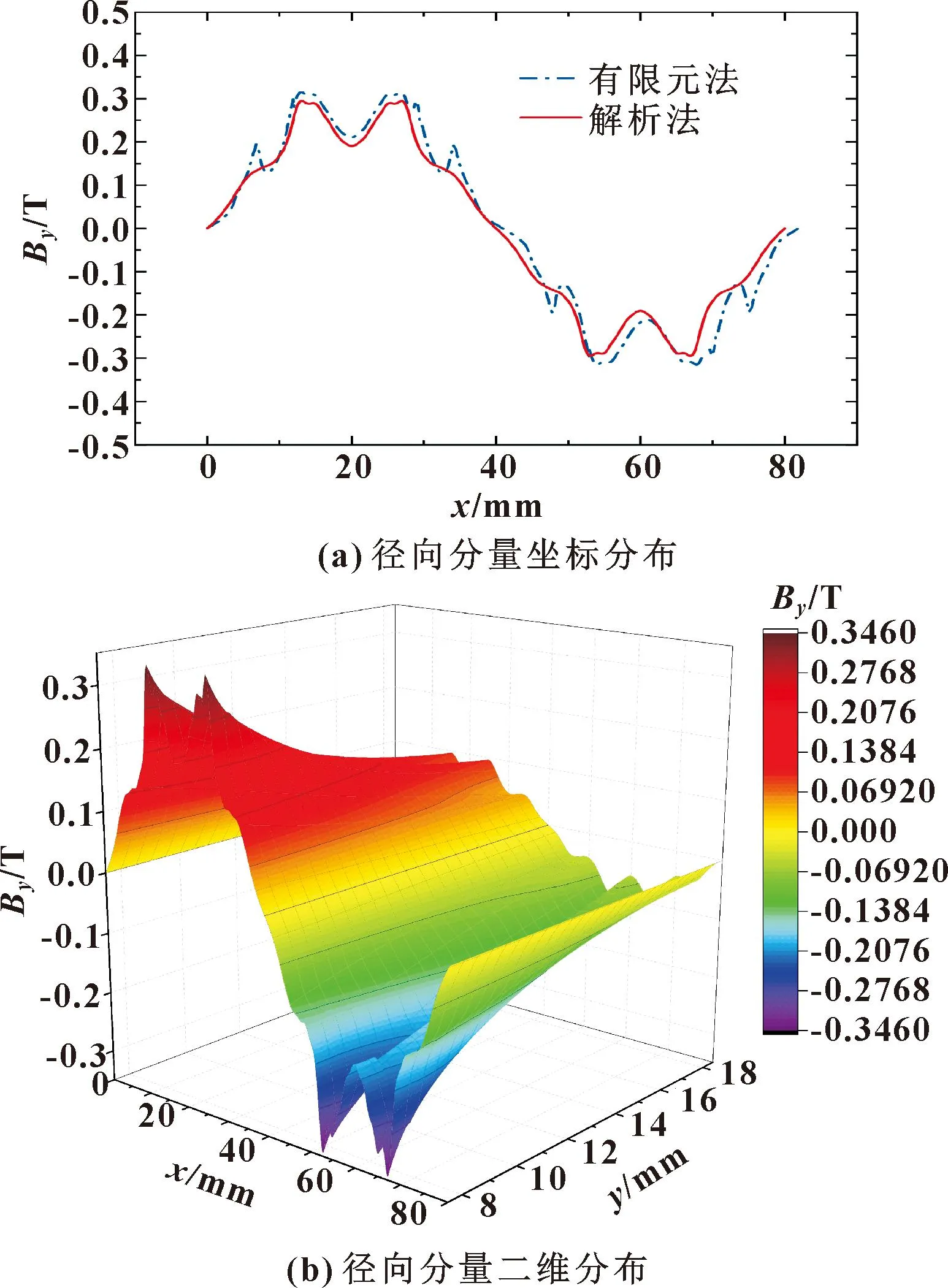
图3 新型电磁缓冲结构的磁通密度分布

1.2 电磁阻力分析

感应电动势可以通过随时间变化的线圈绕组磁链来计算，假设动子产生的位移x0=vt，v为动子运行速度，N为线圈绕组匝数，因此可得

(5)

作用在动子上的电磁阻力由永磁体磁场和绕组线圈电流之间的相互作用产生的。

(6)

将式(5)代入式(6)可得电磁阻力为

(7)

2 直线气缸的动力学模型

气缸工作过程是一个变容积的充放气动态过程。针对新型缓冲结构气缸运动的动力学模型，还需要建立图1中各个腔室的能量方程、温度方程、流量方程及气缸动力学方程。

2.1 气缸各腔室能量方程

根据热力学第一定律可得到进气腔的能量方程为

(8)

V1=A1x+V10

(9)

式中：p1为进气腔压力；k为空气绝热指数；R为气体常数；Ts为气源压力的绝对温度；qm1为流入进气腔的气体质量流量；A1为进气腔气体的有效作用面积；V10为进气腔余隙容积；x为气缸活塞位移；v为气缸活塞运动速度。

对于背压腔而言，在气缸柱塞进入排气腔之前，背压腔和排气腔是完全连通的，因此其气体变化过程与排气腔的状态一致；当气缸进入缓冲阶段之后，背压腔通过溢流阀与固定节流孔将高压气体排出到排气腔，进而排气腔将气体排出，因此整个过程的能量方程为

(10)

(11)

(12)

式中：p2为背压腔压力；T2为背压腔气体的绝对温度；qm2为流出背压腔的气体质量流量；qm3为流出排气腔的气体质量流量；qma为流经溢流阀的气体质量流量；qmb为流经节流孔的气体质量流量；A2为背压腔气体的有效作用面积；A3为排气腔气体的有效作用面积；V20为背压腔余隙容积；V30为排气腔余隙容积；Ls为气缸行程；Lc为缓冲行程。

同时，可得排气腔的能量方程为

(13)

(14)

式中：p3为排气腔压力；T3为排气腔气体的绝对温度。

2.2 温度方程

由于活塞运动速度较高，可将各腔室热力学过程视为绝热充放气过程，因此，由热力学第一定律可得各腔室的温度变化为

Ti=Ts(pi/ps)(k-1)/ki=1，2，3

(15)

式中：Ti为气缸各腔室内的气体绝对温度；pi为气缸各腔室内的气体绝对压力；ps为气源绝对压力。

2.3 流量方程

各气动元件可视为收缩喷嘴或节流小孔的等熵流动，其质量流量可按下式[8]计算：

(16)

(17)

式中：Ae为气动元件有效作用面积；Tu为上游气体温度；pu为上游气体绝对压力；pd为下游气体绝对压力；b为临界压力比。

2.4 气缸动力学方程

气缸运行过程中主要受到各腔室的压力、摩擦力以及电磁阻力作用，根据牛顿第二定律可得气缸的动力学方程如下：

(18)

式中：m为气缸活塞杆、活塞、负载等可移动部件的总质量；Ff为气缸受到的摩擦力。

其中摩擦力模型如下：

(19)

式中：fs为气缸系统受到的静摩擦力；fc为库仑摩擦力；fv为黏性摩擦系数。

3 仿真分析与试验验证

3.1 仿真模型建立

由于前文所推导的动力学方程的非线性的特性，可利用Simulink构建整个动力学计算程序框图并求解。程序框图如图4所示。

图4 Simulink仿真模型框图

整个框图主要包括进气腔模块、背压腔模块、排气腔模块、活塞运动模块等。在仿真模型中，设置活塞行程到达行程终点时立即停止，仿真步长设置为0.000 1 s，采用龙格-库塔法进行求解，即可求解出各腔室气压、活塞速度、位移和加速度等参数的数值解。

3.2 试验测试平台

根据所设计的新型缓冲结构进行设计、加工，并装配到直线气缸中，搭建如图5所示的试验测试平台，包括气动回路、信号采集卡、工控机、传感器等装置。整个测试平台的主要试验设备如表1所示。

表1 直线气缸的缓冲性能测试平台主要实验设备

图5 试验测试平台

3.3 分析与验证

当两种缓冲共同存在时，通过Simulink仿真求解可得在0.5 MPa气源压力下，气缸活塞运动特性曲线如图6所示。可以看出：高速气缸在运行期间，首先加速到1.2 m/s左右，然后基本匀速进入末端缓冲阶段，在新型缓冲结构的作用下，加速度振荡变化，使得速度波动地减至0，从而平稳到达行程终点，达到缓冲效果。

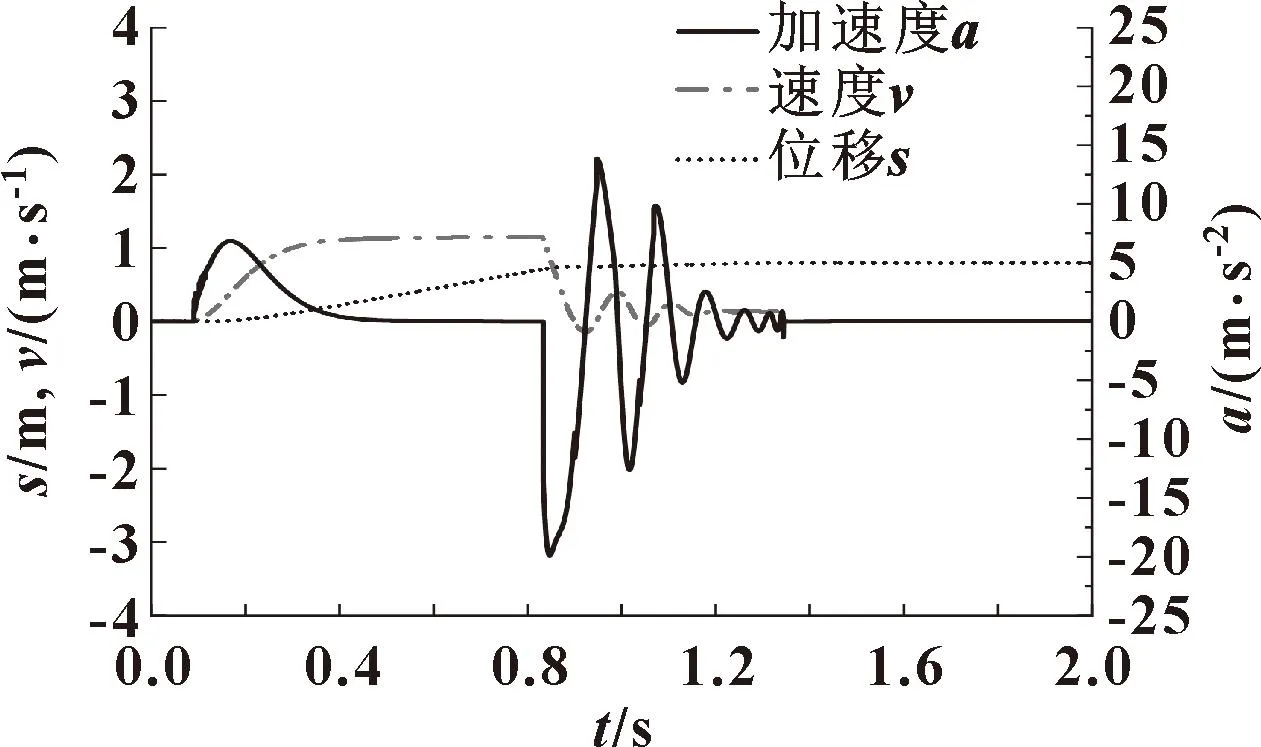
图6 气缸运动特性曲线

图7所示为仿真与试验的动态参数对比，可以看出两种缓冲同时存在时缓冲效果较好，并且从各个状态变量的试验结果以及仿真结果的幅值大小和运行时间对比可以看出，试验曲线与仿真曲线基本吻合，说明所建新型缓冲结构的合理性，以及所建立的高速气缸动力学模型以及仿真模型是正确的。

图7 仿真与试验的动态参数对比

4 不同缓冲结构的对比及分析

针对原有溢流阀缓冲结构以及新型电磁缓冲结构，前文分析了两种缓冲共同存在时的效果，现在针对两种结构分别独立存在时进行对比分析。利用前文所推导的动力学模型，求解得到如图8—10所示的气缸运动特性曲线。

图8 气缸活塞位移对比

图9 气缸活塞速度对比

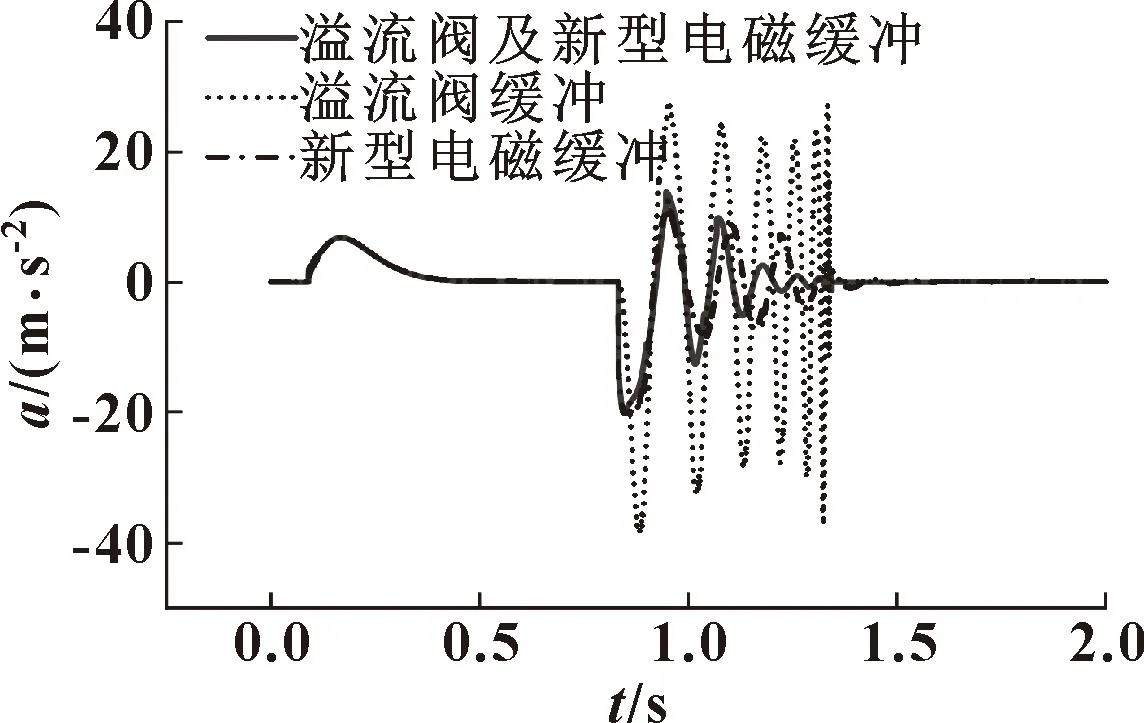
图10 气缸活塞加速度对比

由图8—10可知：两种缓冲共同作用时效果最好，可以使气缸平稳缓冲达到终点；而分别单独作用时，电磁缓冲具有更好的缓冲效果，而气体溢流阀缓冲结构反弹位移、速度、加速度更大，末端冲击大，而且要经过更多次的冲击、反弹循环才能静止下来。

5 结论

本文作者提出一种新型缓冲结构的直线气缸，并通过电磁学理论建立了该缓冲结构的动力学模型。建立新型缓冲结构直线气缸的动力学模型以及仿真计算模型，通过试验数据和仿真结果对比分析，发现两者基本吻合，并且新型缓冲结构使气缸运行到行程末端有较好的缓冲效果，说明所提出的结构的合理性以及动力学模型的正确性。最后对比了溢流阀缓冲、新型电磁缓冲以及两者共同存在时的缓冲效果，发现当两者共同存在时效果最好，新型电磁缓冲次之，传统的溢流阀缓冲效果不理想。文中的研究结果可以为新型气缸的设计提供参考，并且为后续缓冲结构的优化以及能量利用奠定基础。