空间串联机构重力平衡设计方法与仿真分析

胡松华，杨竣皓，孙利雄，李树东

(云南电网有限责任公司保山供电局，云南保山678000)

0 前言

重力平衡又称重力补偿，是指在一定的重力补偿器作用下，某一机构能够在重力环境中保持静态平衡。重力补偿机构广泛应用于机器人中，作为产生反重力和节省能量的被动部件[1]。虽然重力补偿器的设计已经取得了很大的进展，但通常假定重力补偿器的轴线与平衡连杆的轴完全对齐的严格条件，往往在实践中是难以实现的[2]。

在重力补偿机构相关研究中，马保平等[3]研究了手术机器人操作手的定位精度，提出了构件的等效质心位置以实现机械臂的重力补偿，通过有限元对比分析了重力补偿前后的动力学响应特性，验证了重力补偿的有效性。王攀峰等[4]针对丝杆传动并联机构，根据虚功原理提出了含有重力补偿的计算方法，通过反馈力的控制实验验证了重力补偿设计算法的有效性。蒋君侠等[5]针对倒挂式遥控机械手的运动稳定性，提出了重力补偿方法，建立了机械手运动学动力模型，对比分析了各个位姿下的关节轴扭矩情况，表明所提重力补偿算法具有较高的补偿精度。刘岩等人[6]针对机械手负载过程中力传感器的测量，提出了机械手负载端重力补偿策略，建立了重力补偿系统模型，通过MATLAB和有限元联合仿真，分析了所提重力补偿策略的合理性。乔丹等人[7]针对用于人机交互的并联机构，建立了并联机构的动力学模型，在此基础上提出了重力补偿控制器，分析结果表明该机构通过重力补偿后，并联机构的控制精度得到了有效提高。段宇飞等[8]在机器人末端安装了力传感器，在牵引力作用下提出了机器人重力补偿策略，该策略能有效控制误差波动，能够实现力和位移的阶段性变化，提高机器人的控制精度。

使用上述重力平衡机构的机器人，由于重力补偿器的轴线与平衡连杆的轴完全对齐的条件比较苛刻，会导致人机系统过度约束，且容易产生较大的接触力或扭矩，往往在实践中难以实现。本文作者提出一种对被平衡机构旋转中心滑动不敏感的可穿戴式空间重力补偿器的设计方法。该方法不需要将人体关节与补偿器的关节精确对齐，能够兼容因佩戴误差和个体间形态不同而导致的人机关节错位。

1 空间串联连杆的重力等效子系统

图1所示为具有转动关节的连杆空间串联机构示意，其势能Ug[9]可表示为

(1)

图1 空间串联连杆示意

其中：mi表示连杆i的质量；g表示重力加速度；rmi表示连杆i的质心在全局坐标系o-xyz中的坐标。

rmi表示为

(2.1)

(2.2)

(2.3)

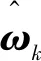
将式(2.1)—(2.3)代入式(1)，得到：

(3)

式(3)表示空间串联机构的重力势能等于n个解耦子系统的重力势能之和，第一项为第n-1个重力等效子系统，第二项为第n个重力等效子系统。重力等效子系统i由连杆i组成，其旋转中心移到全局坐标系o-xyz的原点o，并将从连杆i+1到连杆n的质量之和添加到连杆i的远端，如图2所示。如果每个子系统都是平衡的，即每个子系统的势能保持不变，而不考虑关节的旋转，则串联机构的总势能也保持不变，整个系统是平衡的。而且这些子系统的重力公式是相似的，即它们可以由同一个重力补偿器进行平衡。近端连杆的旋转会影响远端连杆的方向，随着连杆数量的增加，远端连杆的旋转会变得非常复杂。每个子系统都可以看作是一个定点旋转系统，通过分析单连杆定点旋转的重力平衡方法，可以解决各子系统的平衡问题。

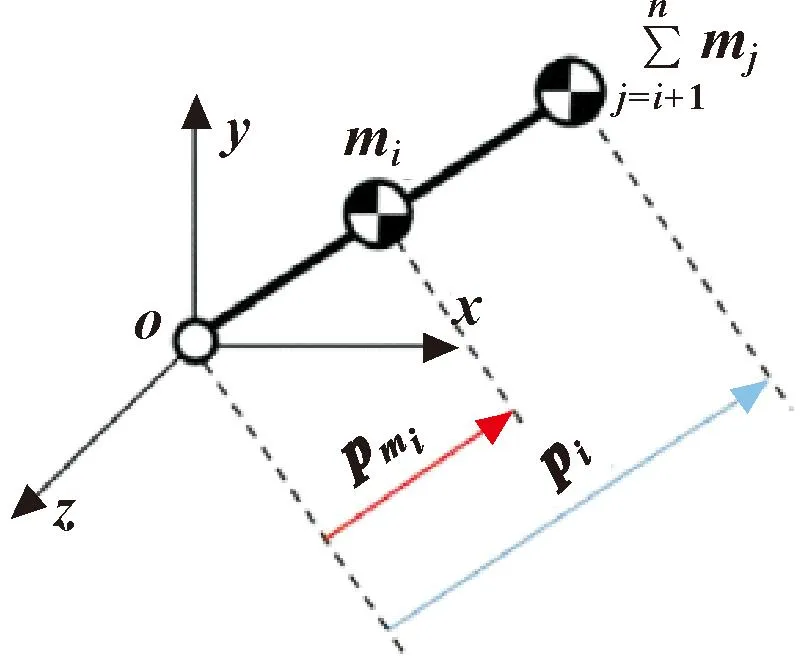
图2 重力等效子系统示意

2 偏航平面单连杆重力补偿器的设计

2.1 单自由度刚体旋转的运动分析

单自由度刚体旋转可分解为耦合的三轴旋转。在确定了连杆的方向后，可以通过逆运动学求解出对应的三轴旋转角[10]，即沿y轴方向的偏航角α、偏航平面中的倾角β和沿连杆纵轴方向的跨度角γ，如图3所示，xy平面为垂直平面，xz平面为水平面，yST平面为偏航平面。如果采用球形关节S连接到基座上的单连杆机构可以平衡，那么其他类型的转动关节也可以平衡。

图3 固定点旋转的运动分解

作者认为只有倾斜角β影响系统的重力势能，忽略角α和γ的影响，分析偏航平面内的平衡条件。系统的重力势能为

Eg=-mglcosβ

(4)

其中：m是平衡连杆的质量；l是旋转中心O到平衡连杆的质心的距离。通过弹簧来平衡系统的重力，弹簧的弹性势能为

Es=1/2kΔx2

(5)

式中：k为弹簧刚度；Δx为弹簧变形。

重力平衡的理想条件是，在任何构型中，重力力矩τg和由关节S处的弹簧力引起的力矩τs之和总是等于零[11]，即：

(6)

式(6)要求Eg和Es与倾角β无关，即Es必须包含cos项来消去Eg的cos项。式(6)成立的充分条件是弹簧变形Δx与倾斜角β之间存在约束，即：

Δx2=c0+c1cosβ

(7)

其中：c0和c1是待定系数。将式(7)代入式(5)，并将得到的Es和式(4)代入式(6)，则有：

c1=2mgl/k

(8)

将式(8)代入式(7)，得到：

Δx2=c0+2mgl/kcosβ

(9)

其中：待定系数c0没有其他约束。实现完美重力平衡的关键是如何物理实现约束方程(9)。

(1)基于余弦公式

根据式(9)，可以通过三角形的余弦定律来实现，即：

Δx2=a2+b2-2abcosβ

(10)

式中：a和b为三角形中偏航角β的相邻边长度；弹簧伸长Δx为偏航角β的对边长度。式(10)的形式与式(9)相同，则有：

c0=a2+b2

(11.1)

k=-mgl/(ab)

(11.2)

(2)基于双角公式

如果将式(9)右侧的项转化为平方函数，则可以简化约束式(9)。cosβ可以通过倍角公式转化为二次型，即：

cosβ=1-2sin2(β/2)

(12)

将式(12)代入式(9)，调整待定系数c0以消除所得方程的常数项，得到：

(13)

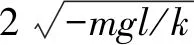
(14.1)

k=-4mgl/r2

(14.2)

2.2 偏航面上连杆的平面重力补偿

基于双角公式的重力补偿器由两个传动子系统组成，即齿轮传动和谐波位移发生器。齿轮传动包括大齿轮(BG)、小齿轮(SG)和耦合器(CP)。BG的节距半径是SG的节距半径的2倍，可知BG始终是齿轮传动的输出环节，它将与谐波位移发生器相连。SG和CP中的一个固定连接到平衡连杆作为输入环节，另一个固定作为底座，由此推导出如图4所示的两种构型。对于串联连杆的重力平衡，构型2更优，因为有足够的轴向空间安装谐波位移发生器[12]，并将用作重力补偿器的部件。

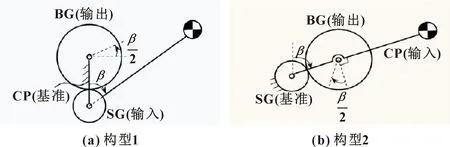
图4 齿轮机构的两种构型

互补谐波位移发生器由两个双滑块机构(DSM)组成，即DSM 1和DSM 2，如图5所示。在每个DSM中，滑块1和滑块2的滑动方向是正交的。在滑块1和滑块2之间设置了一个自由长度为l0的压缩弹簧。互补性是指当一个DSM的压缩弹簧不被压缩时，另一个DSM中的弹簧始终处于压缩状态，这就保证了平衡连杆可以用任何旋转角度进行平衡。在实际应用中，只要BG相对于原始位置的旋转角度ε在一个区间(0，180°)内，即ε∈(0，180°)，则只有DSM 1工作。在接下来的分析和设计中，谐波位移发生器只包含了DSM 1。

图5 互补谐波位移发生器

齿轮传动装置与仅包含DSM1的谐波位移发生器组成平面重力补偿单元，如图6所示。为了使平面重力补偿单元中的弹簧保持压缩状态，即ε∈(0，180°)，CP (平衡连杆)的倾角β应满足约束β∈(0，360°)，即平衡连杆不穿过垂直向上的构型。为简单起见，假设平面重力补偿单元的质心始终在平衡连杆的纵轴上，从旋转中心o到平面重力补偿单元质心的距离lc是恒定的。为了保证完全的重力平衡，包括重力势能和弹性势能在内的势能应该与倾角β无关。根据式(14.2)确定弹簧刚度为

(15)

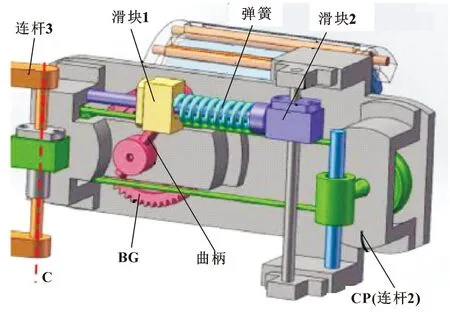
图6 平面重力补偿单元结构示意

其中：lc为旋转中心o到平面重力补偿单元质心的距离；lm为旋转中心o到平衡连杆质心的距离；mc为平面重力补偿单元的质量；m为平衡连杆的质量；r为平面重力补偿单元中的曲柄半径。

3 平面串联机构的重力平衡

为实现n连杆串联平面机构在偏航平面上的完全重力平衡，将同步机构(TBMs)与平面重力补偿单元按传递垂直方向的顺序串联，如图7所示，其中叉(×)表示各部件刚性连接。具体来说，TBMi(i=1,2,…,n-1)由左同步滑轮i(LTPi)、右同步滑轮i(RTPi)和同步带i(TBi)组成，LTPi的角度通过同步带TBi传递给RTPi，LTPi与平衡连杆i的关节Si以及SGi的旋转轴同轴，与SGi固定，RTPi与SGi+1同轴并固定连接。使用Si表示图7中的转动关节i，表示第5节中球形关节i。

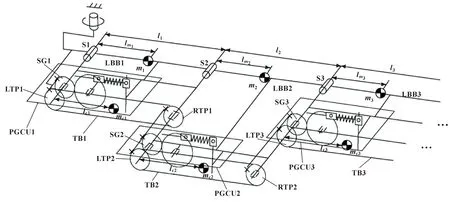
图7 平面串联连杆机构的平面重力补偿机构

由于n个连杆串联机构可视为n个解耦子系统，如果每个子系统都是重力平衡的，那么整个系统的势能将是恒定的，即整个系统的重力平衡就会实现。根据式(3)(15)，平衡子系统i的平面重力补偿单元i的弹簧刚度ki可以确定为

(16)

其中：mi表示平衡连杆i的质量；mci表示平面重力补偿单元i的质量；lmi表示平衡连杆i相对于关节Si的旋转轴的质心；lci表示平面重力补偿单元i相对于关节Si的旋转轴的质心；li表示关节Si轴线到关节Si+1轴线的距离；ri表示平面重力补偿单元i的曲柄半径。

对于一组特殊的空间机构，其近端第一个关节α的旋转轴与重力方向平行，其他所有关节Si垂直于同一偏航面，由于第一关节α不受重力力矩的影响，可以根据所提的平面重力补偿器进行平衡。

4 空间串联连杆的重力平衡

4.1 空间重力补偿单元

具有定点转动的单连杆机构的空间重力补偿单元如图8所示。当平面重力补偿单元以γ角绕其纵轴旋转，且连杆1所在的垂直面可能以相对于原垂直面o-xy的偏航角α转向偏航面时，需对其修改以适应空间固定点旋转。

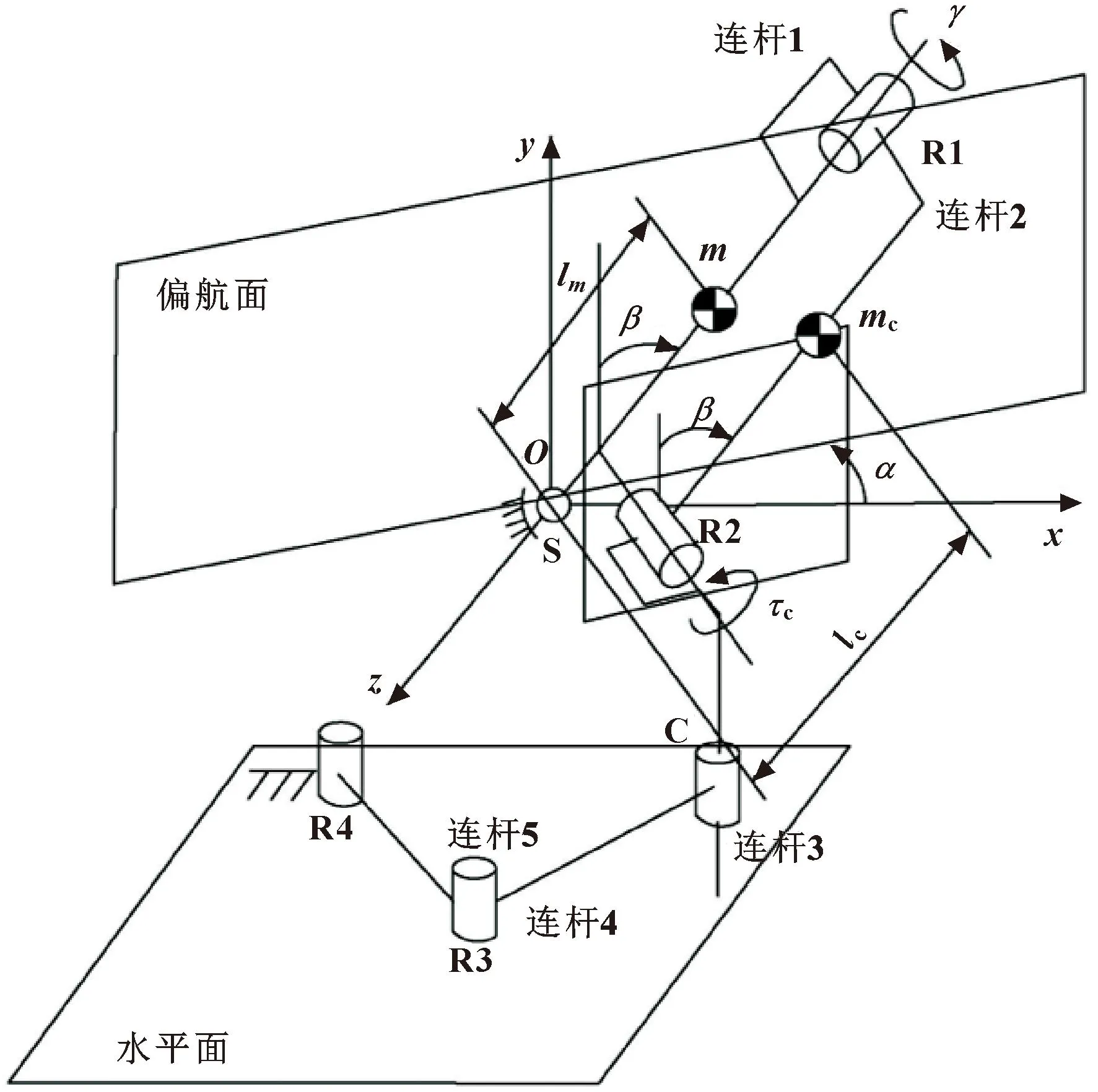
图8 空间重力补偿单元等效原理

对于旋角γ，它对平衡连杆的重力势能没有影响，即自旋运动不应传递到空间重力补偿单元，因此在连杆1与平面重力补偿单元之间的连接处增加了旋转关节R1。对于偏航角α，转动-转动-圆柱链(R4R3C)替换平面重力补偿单元中SG与底座之间的固定连接，连杆3固定在SG上。R4R3C链限制SG的两次旋转，使SG轴保持在一定的水平面内，并阻止SG绕其轴旋转，以传递垂直方向运动或力。在平面重力补偿单元中，SG与底座固定连接，不能绕自身轴旋转。而在空间重力补偿单元中，R4R3C模拟了这种连接，即SG不能绕关节R2旋转，但关节R2可绕垂直方向进行空间平移和旋转，以适应连杆1的偏航运动。平面重力补偿单元替换为关节R2，其轴线与SG的轴线对齐，且有一个等效的扭矩τc由作用在连杆2上的平面重力补偿单元提供，它将最终平衡空间重力补偿单元和平衡连杆的重力。显然，存在一个反力矩-τc作用在连杆3上，连杆1和空间重力补偿单元形成一个由6个关节组成的闭环R4R3CR2R1S。在确定连杆1的方向后，即锁住关节S，空间重力补偿单元应成为具有零自由度的正则构型，即：

(17)

式中：f表示循环的自由度；ci表示关节i的连接数量；d为机构所在空间的维数；l为闭环的个数。

空间重力补偿单元在关节R2处被拆卸分为上、下两部分，如图9所示。下半部分中，R4R3C的3个关节轴是竖直且非共面的，R2的轴线垂直于由连杆3的形状所确定的C轴。这个运动链使连杆3能够在空间中自由平移，并绕垂直轴旋转。关节R2轴线被约束在某个平面1上。上半部分中，关节R1轴线与连杆1的方向HJ重合，经过关节S。关节R2轴线与线HJ垂直，显然四边形IJKL总是一个矩形[13]。关节R2下半部分和上半部分是同一个关节，连接时重叠。关节R2轴线的两个约束，即关节R2轴线在平面1和平面2上，需要同时满足。因此关节R2轴线与连杆1为相互垂直。根据上述几何关系，连杆2与y轴的夹角等于连杆1与y轴的倾角β。

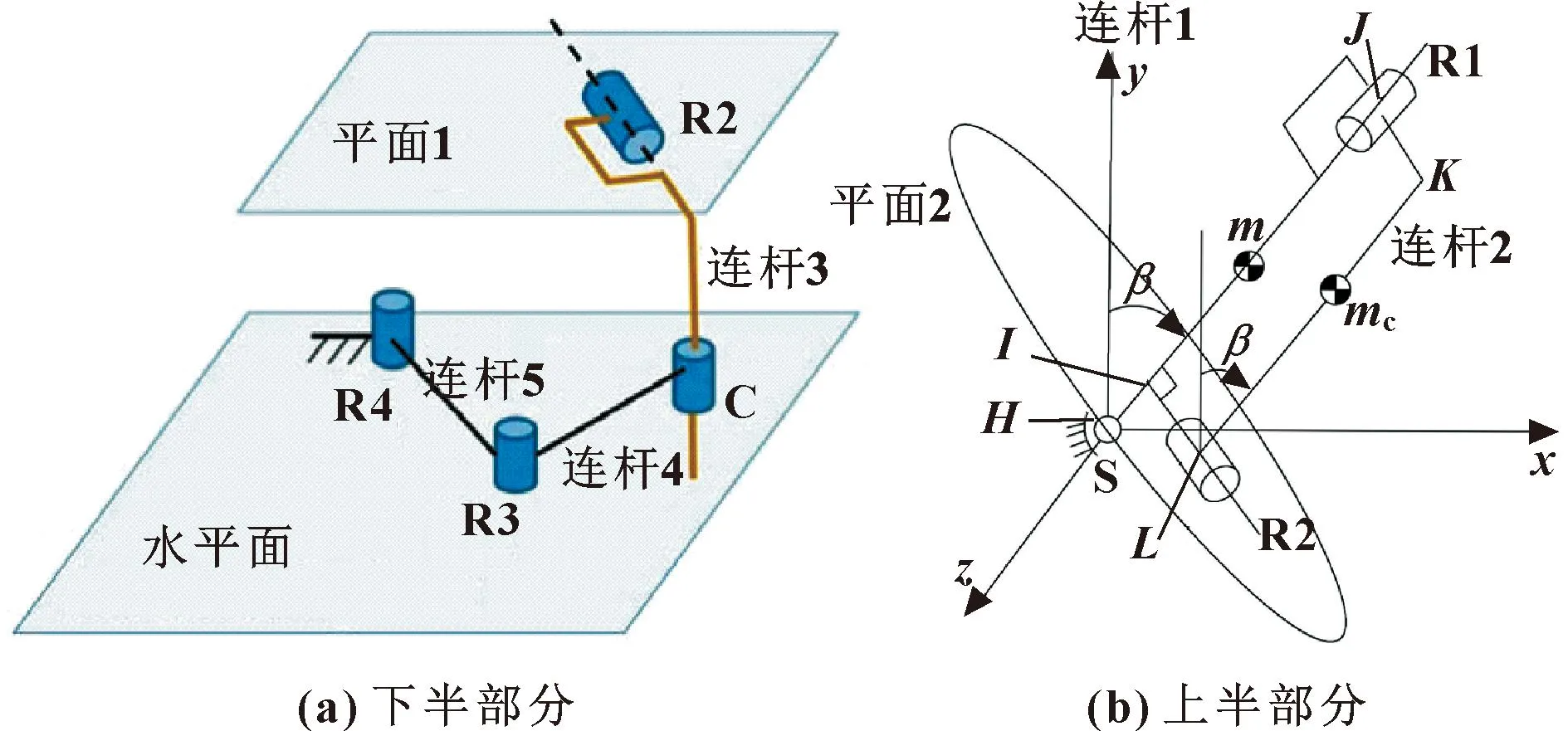
图9 空间重力补偿单元的分解

4.2 空间串联连杆的重力平衡方法

当连杆旋转时，旋转中心往往会漂移[14]，当关节S的中心漂移时，机构不阻止平衡连杆的运动。图10中3种类型关节的不同排列方式导致了不同的重力平衡性能。

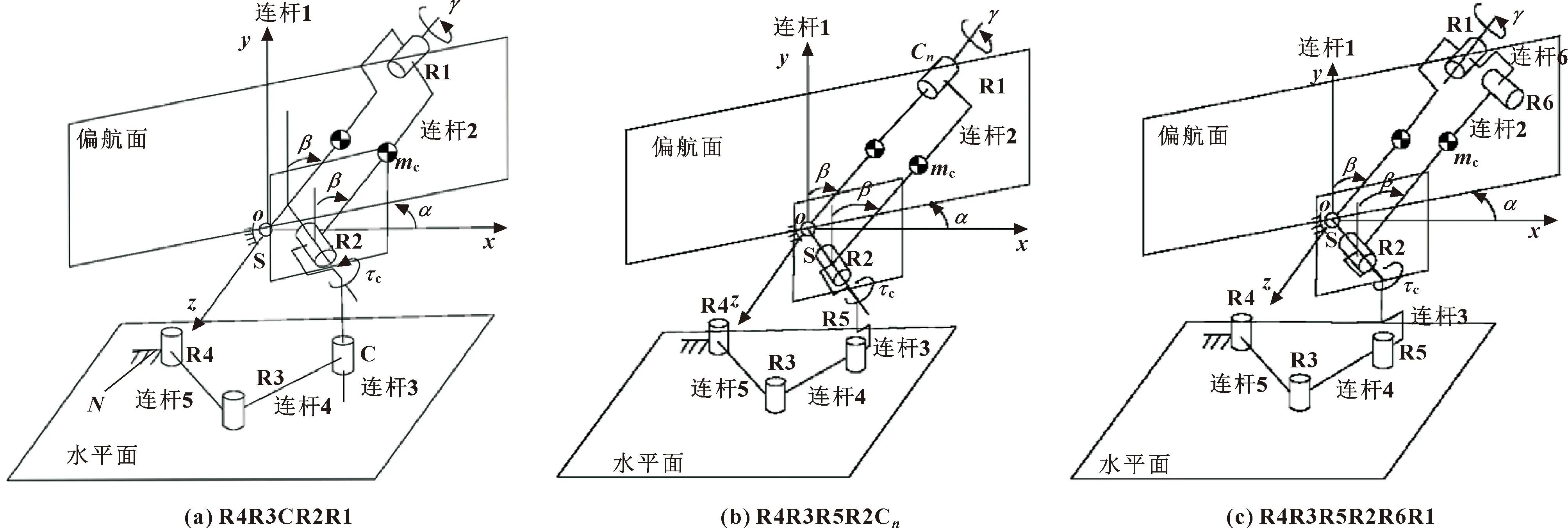
图10 空间重力补偿单元3种类型的静力特性

图10(a)中，关节R2的轴LI不一定要经过关节S的中心H，即机械关节不一定与解剖关节对齐。在连杆1的旋转过程中，始终保留了第4.1节中的运动特性，矩形IJKL的形状没有改变，这使得在按照式(15)确定弹簧刚度时，整个系统的势能保持不变。这样，就实现了完全的引力平衡[15]。当关节S的旋转中心H因人体关节的解剖特征而漂移时，整个机构可视为一个等效系统：关节S的旋转中心H保持静止，但关节R4的旋转中心N沿某一方向具有三维位移。R4R3C链可以完全自行补偿点N的三维位移而不影响其他部位，即关节C以上部位的位姿保持静止，平衡条件成立。R4R3C链的姿态因点N的运动而改变，但对机构的平衡性能没有影响。当关节S的旋转中心H移动时，空间重力补偿单元仍然可以保持完全的重力平衡。

图10(b)中的类型要求关节R2的LI轴精确地通过关节S的中心H，否则当连杆1旋转时，矩形IJKL将不再成立，直线LK与y轴的夹角将不再等于倾斜角β，从而无法实现完全的重力平衡。显然，当关节S的中心H漂移时，就不能满足上述要求，从而无法实现完全的重力平衡。

图10(c)中的类型也需要R2的LI轴通过中心H。其他分析与图10(b)相似。当关节S的中心H漂移时，无法实现完全的重力平衡。

由于篇幅所限，本文作者仅讨论基于空间重力补偿单元型的R4R3CR2R1空间串联连杆的重力平衡方法，重力平衡机构可以通过如图11所示的方法构建。

图11 空间补偿的构建方法

在实际实施中，通过TBM传递垂直方向的方法，关节被平衡地串联在连杆运动过程中，气缸体积较小，不需要较大的空间，且空间重力补偿单元与串联连杆之间能够避免干扰。关节1R4 与底座固定连接，SG1、LTP1和连杆1L3固定连接，RTP1与连杆2L0固定连接。连杆2L3、LTP2和SG2固定连接。

5 机器人重力补偿仿真分析

5.1 仿真设置

文中进行了两次仿真，以验证机器人的重力补偿性能。假设一个人的质量和身高分别为m=70 kg和H=170 cm。根据统计数据，上臂(平衡连杆1)和前臂(平衡连杆2)的长度分别为l1=0.186H=0.316 2 m和l2=0.146H=0.248 2 m，对应质量m1=0.028m=1.96 kg和m2=0.016m=1.12 kg。上臂质心与肩关节S1之间的距离为lm1=0.436l1=0.137 9 m，上臂质心与肘关节S2之间的距离为lm2=0.43l2=0.106 7 m，手被简化为位于前臂远端S3的点质量m3=0.006m=0.42 kg。空间重力补偿单元i的质量为mci(mc1=mc2=1 kg)，空间重力补偿单元i的质心与关节Si轴线之间沿x轴的距离为lci(lc1=lc2=0.06 m)，空间重力补偿单元i的质心相对于肢体o-xy平面的偏移量为loi(lo1=lo2=0.065 m)，空间重力补偿单元i具有半径为ri的曲柄(r1=0.048 m，r2=0.045 m)，根据式(16)确定空间重力补偿单元i的弹簧刚度ki(k1=19 284 N/m，k2= 5 492.8 N/m)。盂肱关节相当于3个转动关节α、β、γ，肘关节简化为关节δ。在后续的两次仿真中，上肢在初始构型中沿x轴的正方向姿势，即点E的初始坐标为rE(0)=(l1+l20 0]T。

(1) 上臂运动的仿真

仿真如图12所示，关节γ、δ被锁定，上肢点E的远端由关节α、β驱动，并在椭球面上做螺旋运动。这个运动在o-zy平面上的投影是一个半径逐渐增大的螺旋，由一个带半轴a和b的椭圆包围，其轨迹表示如下：

(18)

图12 上臂运动的仿真

其中：T为运动的总时间，T∈[0，T]为当前时间；n为T中螺旋的圈数。

从逆运动学分析关节的动作模式，即α(t)和β(t)可以得到解决。在仿真中，T=20 s，n=2，A=(l1+l2)sin80°，B=(l1+l2)sin60°。因此，在仿真过程中，α∈[-80°，80°]，β∈[-60°，60°]。

(2)前臂运动的仿真

仿真如图13所示，在此仿真中，关节α和β始终处于锁定状态。该仿真由两个阶段组成，其对应的运动时间为T1和T2。第一阶段，前臂由关节δ驱动，使远端按五阶多项式定律沿关节E旋转δT1=90°。

(19)

图13 前臂运动的仿真

其中：t∈[0,T1]，五阶多项式施加了约束：δ(0)=δ′(0)=δ′(T1)=δ″(0)=δ″(T1)=0和δ(T1)=δT1。

第二阶段，点E在关节γ和δ的驱动下在椭球面上做螺旋运动。这个运动在o-xy平面上的投影是一个半径逐渐增大的螺旋，被具有半轴a和b的椭圆所限定，轨迹表示为

(20)

其中：t∈[T1,T1+T2]。

从逆运动学分析，在关节的驱动模中式，当t∈[T1,T1+T2]，可以求解γ(t)和δ(t)，在仿真中，T1=5 s，T2=15 s，n=2，A=(l1+l2)sin10°，B=(l1+l2)sin80°。

5.2 仿真结果

在运动学仿真中，外骨骼与上肢之间未发现干扰。仿真1和仿真2的4个关节α、β、γ和δ的扭矩分别如图14和图15所示，比较了上肢佩戴带弹簧(平衡)和不带弹簧(不平衡)的外骨骼时每个关节的期望扭矩，期望扭矩由逆动力学得到。在仿真1中，如图14所示，平衡后β关节内的扭矩降低到非常低的水平(-0.075～0.1 N·m)，平衡前的扭矩为6～14 N·m。由于动作运动较慢，关节α、γ和δ中的扭矩相对较小。

图14 上臂运动平衡前后的关节力矩

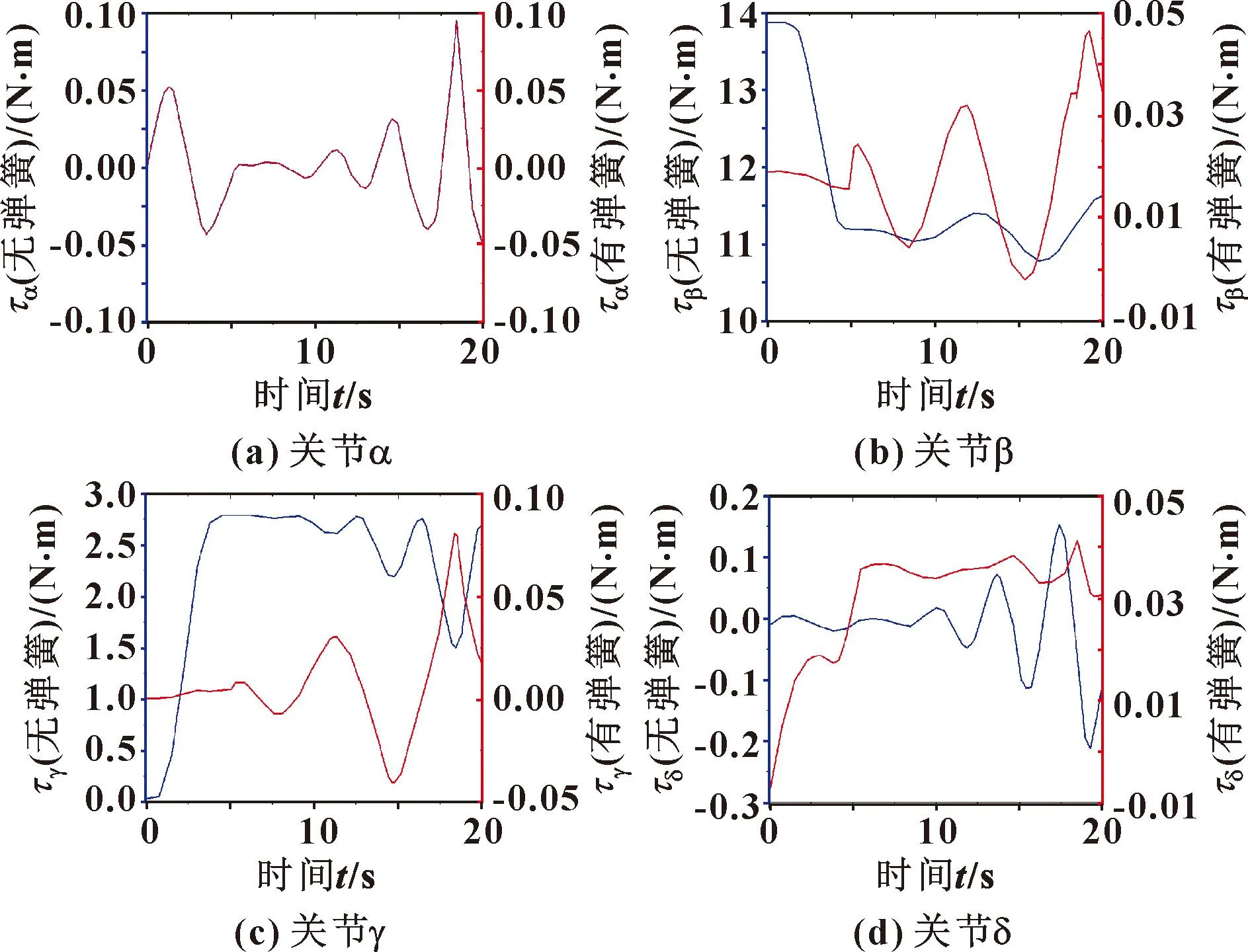
图15 前臂运动平衡前后的关节力矩

在仿真2中，如图15所示，平衡后关节β和γ中的扭矩降低到非常低的水平，分别为0～0.05 N·m和-0.04～0.07 N·m，无弹簧的扭矩分别为10.4～13.8 N·m和0～2.7 N·m。由于动态运动，关节α和δ中的扭矩相对较小。两次仿真的力矩曲线表明：该机构能够很好地平衡自身重力和上肢重力，而不会对其他关节施加其他的力矩，验证了所提机构的重力平衡性能和所提设计方法的有效性。

6 结论

本文作者介绍了一种可穿戴式机器人空间重力平衡机构的设计，可有效避免平衡连杆旋转中心与补偿器轴线不对中的问题。总结如下：

(1)将空间多连杆串联机构的重力势能视为多个子系统的重力势能之和，在平衡连杆的偏航面旋转中，设计了平面重力补偿单元，然后将补偿单元改装成空间重力补偿单元，以适应平衡连杆的一般性旋转。

(2)为平面单连杆设计了重力补偿单元，并推广到通过按顺序组合重力补偿单元和同步带结构来实现平面串联连杆的重力补偿。将RRC和R关节添加到平面重力补偿单元中，从而实现单连杆与空间固定点旋转相平衡。

(3)通过对空间重力补偿的仿真分析，验证了重力平衡性能和所提设计方法的有效性。由于其符合人机耦合系统和重力平衡性能，能在可穿戴式机器人的重力平衡机构中得到有效利用。