基于改进粒子群优化算法的分数阶PID控制器
李小松 孙志敏
摘要:针对控制系统控制性能不稳定的问题,实践中可在控制系统里设定一种分数阶PID控制器。相比于整数阶PID控制器,分数阶PID控制器增加了λ和μ两个控制参数,这样可以让控制器在控制过程中拥有更好的性能,但同时也使得参数整定使用更加困难。为了更容易地求出控制器的参数,需要使用改良过的粒子群(PSO)优化方法来进行整定,将时间误差绝对值(ITAE)准则应用到控制器的控制过程当中,可以快捷地得出分数阶PID控制器的优化参数。通过对常规PID控制器与分数阶PID控制器的仿真结果进行对比,经过优化后的粒子群算法得到的参数在运用到控制系统中时会得到的更好的效果,说明了优化后的分数阶PID控制器的控制效果要优于整数阶PID控制器的控制效果。
关键词:分数阶PID;粒子群算法;参数整定
doi:10.3969/J.ISSN.1672-7274.2024.03.023
中图分类号:TP 273 文献标志码:A 文章编码:1672-7274(2024)03-00-03
随着近年来科技的不断进步,工业和医疗对科技的要求也越来越高。在20世纪90年代Podlubny提出,将传统PID控制器引入微分阶次μ和积分阶次λ,增加了FOPID控制器的控制范围[1-2],控制精度大大提高,在被控对象的控制过程中也可以更加灵活地操作。
相比于传统PID控制器,FOPID控制器增加了两个参数,在参数整定方面,FOPID控制器变得更加复杂。传统控制中采用整数阶PID控制器是因为缺少求解分数阶微分方程的数学工具,FOPID控制器虽然可以解决许多复杂难题,但是参数整定的问题如果不能得到有效解决依然不能得到广泛推广,于是参数整定的问题成为分数阶PID控制的研究热点。相比于常见的频域幅值裕量法和主导极点法,采用优化方法可以缩减很多工作量。优化方法最重要的一环就是获得优化参数,在控制系统的控制过程中正是借用这些参數提升系统性能的,利用粒子群(Particle Swarm Optimization,PSO)优化算法是当下获取参数运用比较广泛的新型算法。
1 分数阶微积分及分数阶PID控制器
1.1 分数阶微积分
整数阶微积分通过延伸的方式推出分数阶微积分,只要不是整数阶次的微积分就可以被定义成分数阶微积分。若想实现多种阶次的微积分也需要依靠分数阶微积分,分数阶微积分的算子能在整数阶微积分算子的基础上拓展得到,表达式如下:
式中,为分数阶微积分算子;下限中积分或微分用a表示;上限中积分或微分用t表示;阶次用表示。下面四个公式是分数阶微积分中使用最多的定义。
(1)Caputo表达式。
式中,α<0。
(2)Cauchy表达式。
式中,C为开区域的光滑曲线。
(3)Grunwald-Letnikov表达式。
式中,为函数的二项式系数;[(t-α)]可以趋向于∞。
(4)Riemann-Liouville表达式。
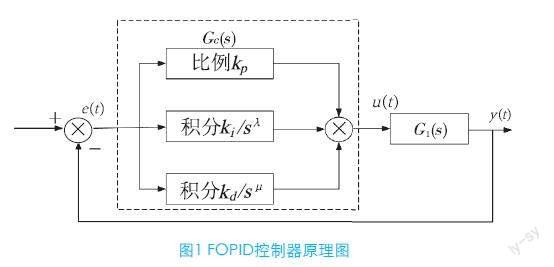
1.2 FOPID控制器
FOPID控制器和传统PID控制器的不同之处就在于FOPID控制器多了两个可以任意调整的参数,其传递函数为
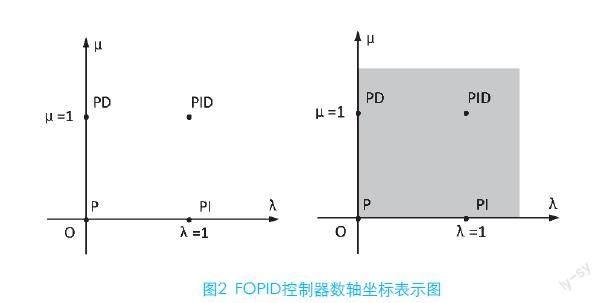
图2是FOPID控制器在数轴坐标下的表示,数轴中用横坐标表示积分阶次,用纵坐标表示微分阶次。通过横纵坐标的改变可以得到常见的PID控制器,在特殊情况下也会得到另外两种控制器。
从图2中得到的信息有很多,例如,图2中的阴影部分涵盖的是λ和μ的所有值,得到PD控制器只需要将λ用0表示μ用1表示,得到PI控制器只需要将λ用1表示μ用0表示。对于整数阶PID控制器我们将λ和μ共同赋予数字1即可得到,由此可见分数阶PID控制器可以变成上述三种控制器。
整数阶PID控制器中的微分环节中有固定的相角超前,通过产生修正信号来改善系统的稳定性,并提高系统的动态性能。但是固定的相角超前可能达不到理想的控制效果,而微分环节在分数阶控制器中可以任意改变μ的值,这样可以使相角超前在0°~180°之间任意改变,直到调节到最适合被控系统的值。大量实验数据结果证明,在震荡频率,控制时间和超调量这些重要数据都受到u值干扰的情况下,u值的选择极其重要并直接决定了系统的各项指标。表示相角滞后的PID控制器,可以提高系统的稳态性能,但也降低了系统的动态性能,可能使系统响应太慢,大大延长了调节时间,从而使得与预期的结果相差甚远。代表在控制器中占有重要意义的积分环节,由于λ可以任意改变其值,所以相角滞后可以在0°~180°之间任意变化,使得调节时间和超调量减小,稳态精度提高,这样可以更好地使系统达到稳定,同时也保证了系统的动态性能和稳态性能。
2 粒子群算法和仿真实验
选取文献[3]中的经典的分数阶被控系统
用粒子群算法对被控系统设计FOPID控制器主要任务是参数的整定,、、、μ、λ这5个参数是需要被整定的。
第一步对粒子群在五维空间中选择最优位置,设定由5个参数的量子位置组成的向量是,,将量子位置转为优化解区域的值来计算量子粒子适应度值,有如下规则:
式中,为第d个参数优化的下限值;为第d个参数优化的上限值;为第k次迭代中第i个量子粒子在第d维中的位置。
表示第i个量子粒子的个体最优位置,表示在位置最优情况下量子粒子群的整体,用以下的公式表示整个演变过程中粒子i坐标和相角的改变轨迹:
设粒子数;最大迭代次数;;,学习因子。
第二步在確定具体哪个函数指标性能较好时,阶跃响应时间同误差绝对积分(ITEA)的结合结果更好,因此在适应度函数的选择上使用了ITEA,即:
取得计算步长,。
其结果函数值大小与控制器的控制性能相关,函数值越小,则整定的参数值越好,控制系统的动态性能也越好。利用上述方法得到一组参数数据:=99.75,=81.34,=92.16,λ=1.09,μ=1.67,得到分数阶控制器:。
比较其他设计方法设计出的FOPID控制器作用在相同被控对象下的情况。
第三步用极点阶数法、差分进化算法和幅值相位裕量法得到4个不同的FOPID控制器。
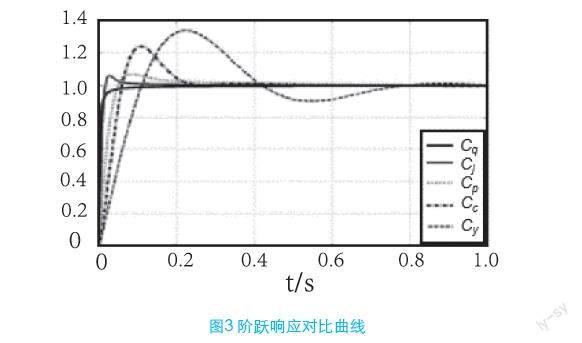
得到的阶跃响应对比曲线如图3所示。可见用粒子群算法得到的FOPID控制器控制的系统调节时间超调量都很小,整个系统的动态特性优于其他方法得到的FOPID控制器。现给一传递函数:
采用ITAE准则指标优化后得到优化后的FOPID控制器参数,,,,,得到FOPID控制器的传递函数,用常规PID控制器设计方法得到。
通过上述仿真结果可知,FOPID控制器的控制性能明显好于一般意义上的PID控制器。将普通的PID控制器与结论推出来的控制器做对比,本文得到的控制器的准确性和快速性更好,稳定后的误差也更小,超调量变小,调节时间也变短,表现出很好的鲁棒性和稳定性。
3 结束语
在确定FOPID参数的实验中,使用了多种不同模式的办法,相比于其他求FOPID控制器参数的算法,采用经过优化后的粒子群算法得到的FOPID控制器效果表现更好。仿真实验也从多个角度证明了分数阶PID控制器和整数阶PID控制器存在本质的区别,在具体实验中也可以看出,优化后的分数阶PID控制器控制效果较好,稳定性得到了明显的改善,超调量更小,调节时间也更短。在稳定性,准确性和快速性方面都取得了更优的效果。
参考文献
[1] 刘璐,单梁,蒋超,等.基于改进粒子群算法的分数阶系统参数辨识(英文)[J].东南大学学报(英文版),2018(1):6-14.
[2] 王心,郭伟,魏妙.基于粒子群优化的分数阶PID滑模控制参数整定[J].测控技术,2017(12):63-66.
[3] Engineering - Mechanical Engineering; Data from Warsaw University of Technology Advance Knowledge in Mechanical Engineering (Plc Based Fractional-order Pid Temperature Control In Pipeline: Design Procedure and Experimental Evaluation)[J]. Journal of Engineering, 2020,67(3):102-106.

