探寻本质 触类旁通*——一道解几中线段比值问题引发的探究

广东省中山市烟洲中学(中山市周建刚名师工作室) (528401) 周建刚 闫 伟

1 试题呈现

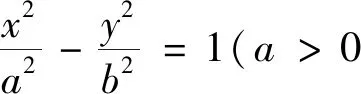
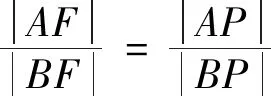
本题为2023年山东省枣庄市3月份高三模拟试题第21题,该题目的命题背景平和,内涵深刻,知识层面主要考查双曲线的标准方程、几何性质、直线与双曲线的位置关系、线段比值问题,是解析几何专题中的常规题目;重点考查学生运用坐标法研究圆锥曲线中的存在性问题,侧重考查学生的数学运算、逻辑推理等素养;试题分两问,第一问结合双曲线的焦点坐标和渐近线方程求标准方程,属于基础题,第二问寻找满足线段比值相等的点P,属于圆锥曲线中探索性的问题,思维难度适中,但运算量较大,需要借助角平分线的性质以及根与系数的关系进行变形转化,对学生的能力要求较高,较好地体现了对直线与圆锥曲线的核心内容和基本思想方法的考查[1].

2 试题推广

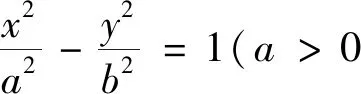
将题目中的右焦点F改为x轴上的任意一点,不包含双曲线的顶点和原点,其他条件不变,是否还存在点P满足上述条件?经探究得到:

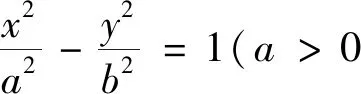
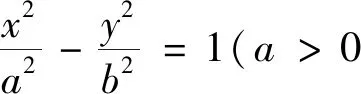
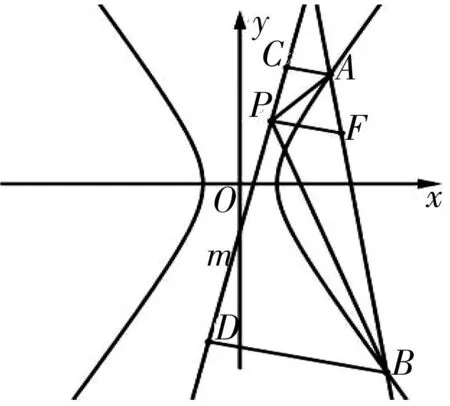
图1

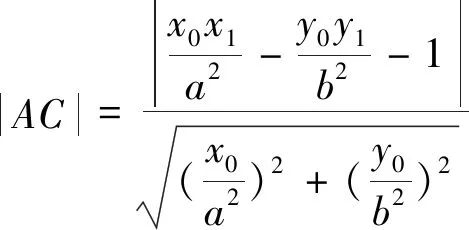
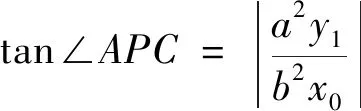
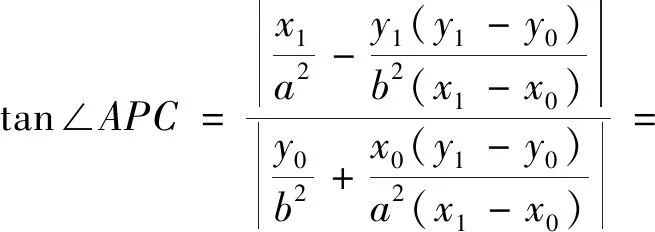
对于直线l与双曲线交于不同支的两点,该结论同样成立,此处不再赘述,留给感兴趣的读者自行证明. 上述性质中F点的纵坐标为零时,就是性质2的结果,即它是性质3的特殊情况.

3 类比探究

将上述性质引申到椭圆和双曲线中,可得到以下性质:

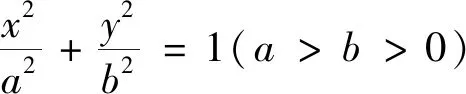
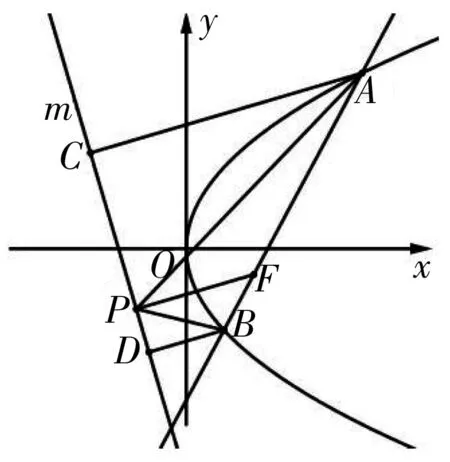
图2

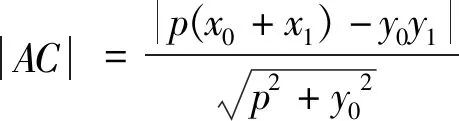
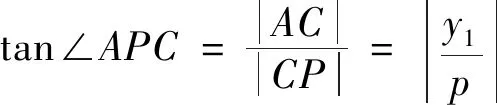
上述结论中,直线m实际是点F关于圆锥曲线对应的极线,因而P点本质上是过F点与其对应极线垂直的垂线与极线的交点,因此本文中的性质3-5可以进一步统一概括为:

极点与极线是解析几何中的一条重要性质,它在圆锥曲线问题的探究中具有十分重要的应用,本文对这一线段比值问题的探究很好地佐证了这一点[2]. 近些年很多高考题和模拟试题都以极点、极线相关结论作为命题的落脚点,在复习备考的过程中,引导学生掌握圆锥曲线的极点极线理论不仅能快速高效地解决与之相关的试题,还能有助于学生更深刻、更全面的把握试题的本质[3].