基于螺旋理论的3 自由度并联机构运动学分析

叶 秋 ，夏宁明 ，宋代平

（重庆大学机械与运载工程学院，重庆 400030）

0 前言

在汽车制造技术中，利用机器人进行协同甚至自主完成加工、美化工作可以大幅度提升加工制造效率[1-2]。现阶段，相关企业主要采用串联机器人协同工作，但此类机器人存在运动刚度低、机构不稳定、承载能力小等不足，因此，亟需设计一款以并联机构为主要执行部件的机器人来解决这些难题。并联机构是将运动平台与静平台通过多个运动支链连接，使得运动平台获得多自由度的机构，其具备刚度高、结构稳定、承载能力大、精度高、响应速度快等诸多优势。近年来，少自由度并联机构研究吸引着许多学者的目光[3-4]，少自由度并联机构相较于6 自由度并联机构而言，其运动空间更理想，定位能力优异、运动学求解过程较简单，在机床加工、零件打磨、手术机器人等使用场景都有参与[5-7]。除此之外，将3 自由度并联机器人与2 自由度机器人串联可进一步扩大其运动范围，提高工作效率，使机构适用于更加繁杂的运动场景。例如，Liu 等[8]以3-SPS-S（S-球副，P-移动副）并联机构为基础设计水下机器人，使得机器人的运动响应和运动精度满足使用要求；Exechon 机器人则以2-UPR-SPR（U-万向副，R-转动副）为基础建立冗余驱动并联机构[9]，使得机器人获取优质的运动特性并满足使用工况要求；Chong 等[10]利用3_PUU并联机构设计涡轮叶片打磨机器人；Zuo 等[11]利用UPU支链构建足弓和脚踝的固定器。

本文以3 自由度并联机器人为研究对象，重点关注该对接机器人的运动学分析，考虑机构寄生运动[12]，运用螺旋理论推导机构运动学方程，利用运动学仿真软件对所设计的机器人进行运动学仿真，验证分析运动学求解的正确性。

1 机器人介绍

本文设计了一款以并联机构为主要执行部件的机器人，用于协助完成汽车车体加工与表面喷漆工作，其整体外观设计如图1 所示。机器人主要由AGV、连接部段、3 自由度并联机构和作业部件组成，AGV 负载运载整体执行部件在厂区内作业；2 自由度连接模块用于实现AGV 与执行部件的连接与供电；3自由度并联机构作为支撑机构，其前端与作业部件串联，实现车体表面加工的同时增加了执行部件的刚度和承载能力等。

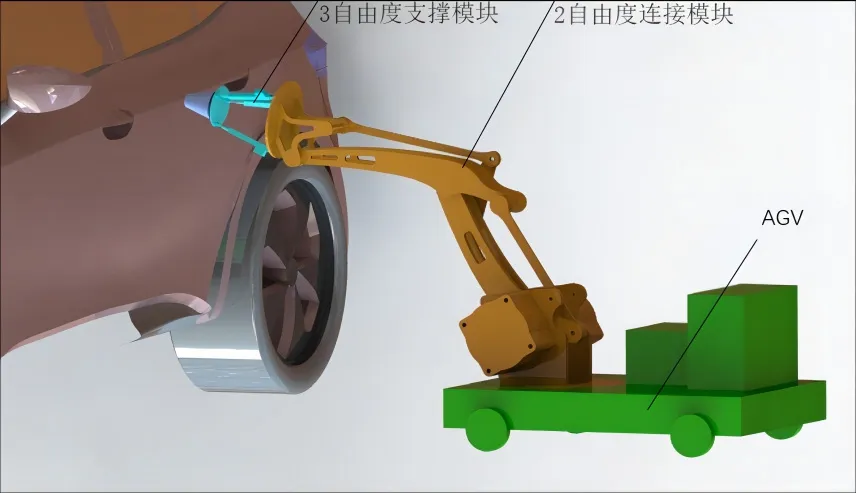
图1 车身加工机器人

所设计的3-RPS 样机如图2（a）所示，并联机构的3 维模型如图2（b）所示，其中，O-XYZ为机构静平台坐标系即全局坐标系，p-uvw是机构的运动坐标系，参考点p位于机构运动平台的中心，u、v、w轴的初始方向与X、Y、Z轴一致；Ai-xiyizi(i=1,2,3)是位于每条运动支链的坐标系，坐标原点Ai与支链中R 副的运动参考点重合。该机构由3条运动副一致的RPS支链组成，整个结构绕Z轴旋转对称布置。

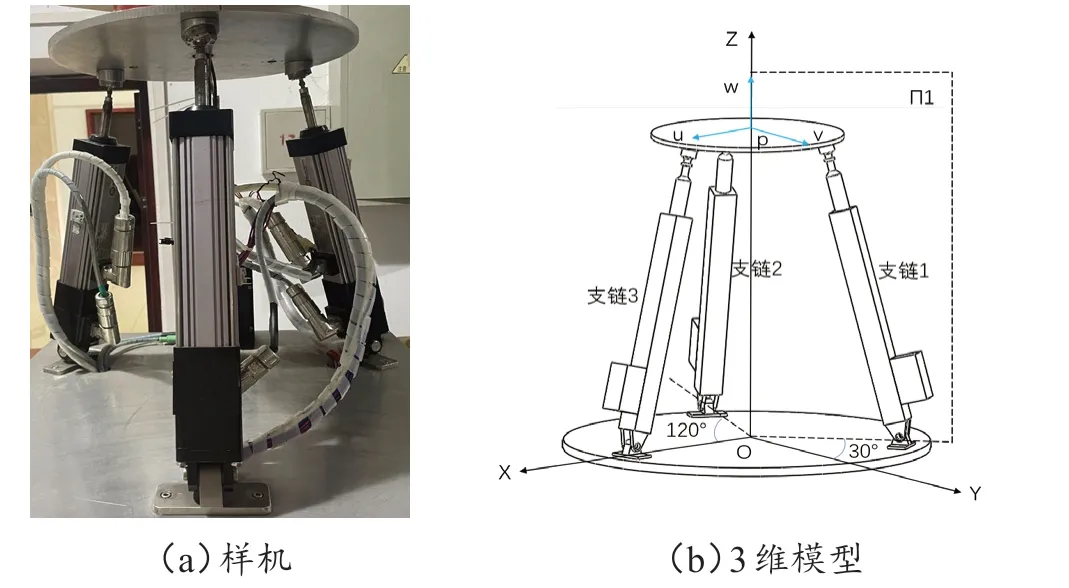
图2 3-RPS 样机模型

以支链1 为例，机构中的支链运动示意图如图3所示，AA´为支链转动副轴线，球铰运动可以看作是绕3 条互相垂直的轴线转动，则设定BB´、CC´、DD´分别是运动支链中球副的转动轴线，为方便计算与求解，将三个轴线的运动方向设置为与支链的坐标系Ai-xiyizi一致，支链1中移动副的运动轴线为EE´。

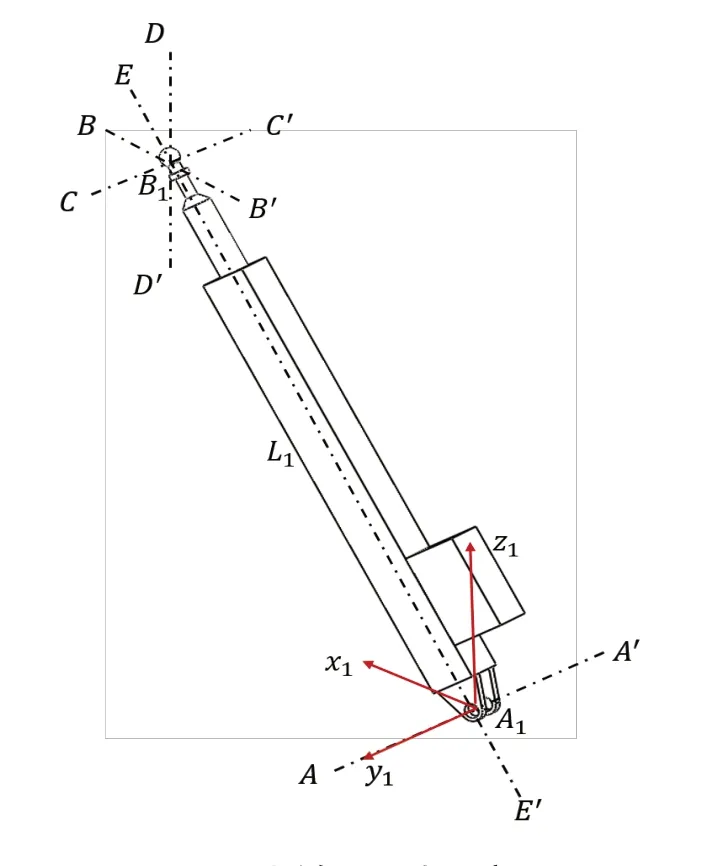
图3 支链1运动示意图

2 自由度分析

鉴于常规G-K 公式计算机构自由度只能获取机构自由度数目却无法得到机构运动种类和运动方向的特点，故采用螺旋理论对机构运动进行分析[13]。刚体运动和受力运动可以采用Plücker 坐标（六维）表示，螺旋的常规表达为$=(s;so)，当$◦$r=0 时，可以判定$r为$的反螺旋，即$、$r互逆。对于机构而言可以得到：以$r为方向的外力加载于刚体的运动$上，此外力不做功，即表示该机构在约束螺旋$r方向的自由度被限制。对于并联机构而言，机构各支链中运动副共同作用形成支链约束螺旋$ri(i=1,2,3)，各约束螺旋沿支链施加于机构末端运动平台。

机构各支链的约束螺旋$ri(i=1,2,3)集合形成的作用即产生对整体机构运动平台的约束，进一步对约束螺旋$r集合求反螺旋，得到并联机构动平台的运动螺旋，即为机构的运动自由度。机构的运动模型简图如图4 所示，动坐标系p-uvw固连于动平台，轴线与基坐标系轴线方向一致，p点作为运动参考点，位于动平台中心，支链坐标系Ai-xiyizi的z轴与基坐标系的Z轴同向，x轴由Ai指向O点，y轴根据右手定则确认，r为运动平台半径，R为机构静平台半径，Li为AiBi的长度，以Li的变化值作为主动件移动副的运动距离。

图4 机构运动简图

由于机构绕Z轴旋转对称布置，故只需要对机构的一条支链进行分析，即可获得普遍性。支链1 的机构运动简图及运动螺旋如图5 所示，由此可以获得支链中各个运动副的运动螺旋。

图5 支链1 运动简图

式中：αi为支链中R 副的转动角度，i=1,2,3；cα与sα分别为cos与sin运算。

进一步在支链运动坐标系Ai-xiyizi下对支链的运动螺旋组求反螺旋，以获取支链运动约束：

支链局部坐标系Ai-xiyizi(i=1,2,3)与基坐标系O-XYZ存在旋转变换矩阵为：

上式即为三条支链对运动平台的约束，将移动副驱动设为定长，即L1=L2=L3=L，转动副R 的转动角度设定为α1=α2=α3=α，对式（5）中的约束螺旋系求解反螺旋，即可得到机构运动平台的运动螺旋：

由式（6）求解的运动螺旋得出机构运动平台具备3 自由度，其中包括沿Z轴的移动自由度和沿X轴、Y轴的转动自由度。

3 运动学求解

机构运动学求解包含机构逆向运动学求解与机构正向运动学求解，逆运动学研究主要解决给定运动机构参考点运动Xp=[Mz,φ,ø]T，通过建立运动学方程求解驱动参数ΔL=[l1,l2,l3]T，（其中，l1,l2,l3分别为机构支链中移动副运动量即Li的变化量）；正运动学则刚好相反，给定支链中主动件的运动值ΔL=[l1,l2,l3]T求解，即可获得机构动平台运动。

3.1 寄生运动分析

由于少自由度并联机构存在寄生运动，即在机构运行过程中，运动参考点会因机构设定自由度运动产生其他自由度方向上的运动（如当本并联机构进行绕X轴转动或绕Y轴转动时，会伴随出现X或Y自由度上的移动）。因此在对机构进行运动学分析前需要先求解机构运动参考点的寄生运动[Mx,My,γ]，为求解机构的寄生运动，将机构出现寄生运动的位姿投影于基坐标系的OXY平面，如图6所示。

图6 OXY 平面投影

图中的OAi、OBi分别表示Ai、Bi在OXY平面的投影，由图可以看出Ai、Bi相交于O点，即：

其中，pRm=Ry(φ)Rx(ϕ)Rz(γ)，为运动参考坐标系相对于基坐标系的变化，p=(Mx,My,Mz)为机构运动平台参考点的位置向量。球铰参考点相对于运动坐标系的位置为：

其中，需满足以下条件：

将所求得的点代入式（8）中，即可获得共线运算方程：

化简后可以得到：

同理，可以获得B2、B3在OXY平面的投影坐标OB2、OB3，代入式（8）求解共线方程：

结合式（15）与式（16），利用消元法获得机构寄生运动Mx,My与ϕ,φ的关系。

将式（20）中求得的Mx,My的值代入，可以求解得到运动平台寄生运动γ值与ϕ,φ的关系。

通过以上分析，能够完整求解出所设计并联机构的所有寄生运动Mx,My,γ，并可进一步写出机构动平台完整的运动位姿Mx,My,Mz,ϕ,φ,γ。

3.2 逆运动学求解

用上一章对于完整寄生运动的求解和机构运动参考点位姿表示，可以建立机构的逆运动学方程，即由参考点位姿获取移动副的运动轨迹。与许多并联机构逆运动学求解过程一样，采用支链封闭解的形式建立逆运动学方程，在已知位姿的情况下，支链球铰运动参考点Bi相对于基坐标系的位置向量为：

式中：Ai为Ai相对于O的位置向量，Li为移动副AiBi的向量。

由式（21）可以计算得到主动件运动距离，即用支链中AiBi的长度减去移动副初始距离L0i：

3.3 正运动学求解

正运动学方程求解同样以前文所提的支链中的几何闭环关系作为出发点，利用机构雅可比矩阵构建机构运动学方程。将式（21）中的闭环关系分别对时间求导得到：

由此，则可以利用̇X=(vp,ωp)T、̇l=(̇l1,̇l2,̇l3)T的形式表示机构动平台运动和主动件运动，故将式（24）改写成机构雅可比运算形式，即：

为获取̇X与̇l的关系，由式（25）的矩阵运算进行求逆变换，可得Ja-1Jp∙̇X=̇l，Ja-1Jp-3×6可进一步得出机构驱动与机构动平台姿态的速度映射关系。但由于上式中的̇X=(vp,ωp)T是六维向量，机构运动自由度为3，则需要将其化简为线性无关的3维向量̇Xp=[̇Mz,̇ϕ,̇φ]T。将Mx,My,γ分别对Mz,ϕ,φ求偏导，得到̇X和̇Xp的关系：

进一步将式（30）代入式（27）中，便得到机构输入、输出方程：

其中，J=Ja-1JpJd-3×3，与其他并联机构正解求解方法相同，利用牛顿迭代法，限制机构运动副范围与运动件行程，即可获得机构运动学解。

根据所列方程与机器人工具箱编写MATLAB 程序，设定机构参数值r=90 mm，R=175 mm，li∈[0，150]，使得机构在不同姿态下运动，如表1 所示，对处于不同运动工况下的机构进行运动学求解。

表1 机构运动工况

本设计采用对称布置，为便于直观进行运动分析，在分析过程中均给予运动参考点正弦运动，通过分析可以得到机构在不同运动姿态下主动件的运动轨迹变化，结果如图7 所示。图7（a）为运动平台Z向移动时移动副的运动轨迹，图7（b）为运动平台绕X轴转动时移动副的运动轨迹，图7（c）为运动平台绕Y轴转动时移动副的运动轨迹，图7（d）为运动平台绕X、Y轴耦合转动时移动副的运动轨迹。

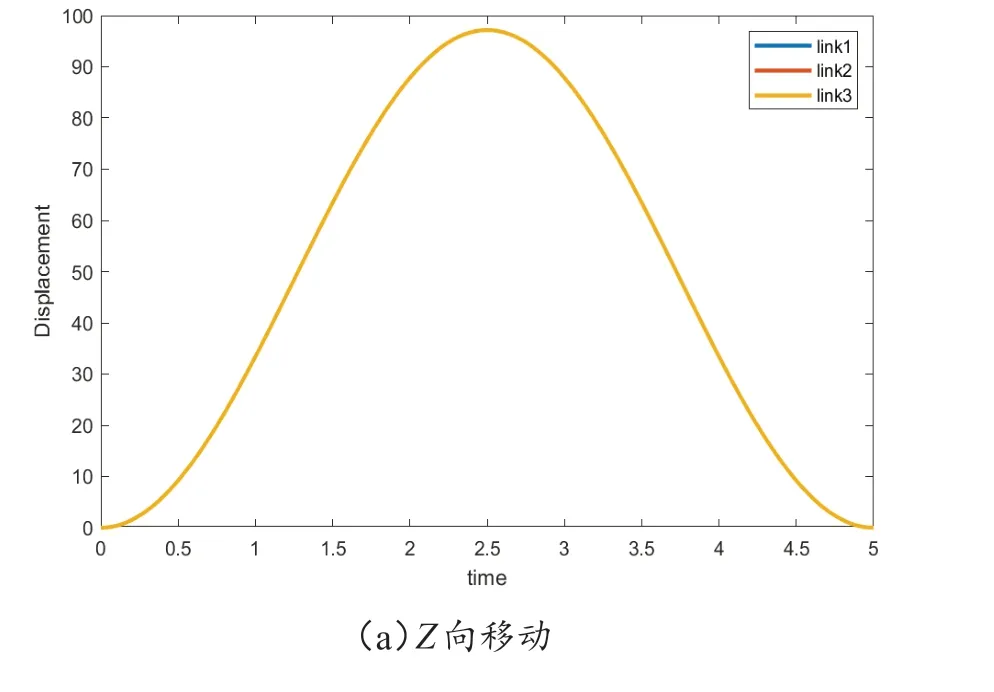
图7 运动分析结果

4 运动仿真

为了进一步验证本设计中机构分析的合理性，将建立好的三维虚拟样机导入Admas View 软件中，设定机构支链中的运动副与运动约束，同样规划如表1所示的正弦运动轨迹与姿态，Z向移动工况仿真设置如图8 所示。由于机构具备寄生运动，在设定运动参数时需要释放寄生运动的3 个自由度给予其自由状态，对其运动学进行仿真分析获取运动结果，如图9所示。图9（a）、图9（b）、图9（c）、图9（d）分别对应表1 中所设定的不同运动工况的Admas 仿真结果，由仿真分析结果得出：仿真值与分析值的误差不到3%，在可忽略范围内，验证了运动学分析过程与结果的正确性，可以利用此结果进行进一步的机器人运动控制设计与相关研究。

图8 Z 向移动工况仿真参数设定

图9 运动仿真结果

5 结论

1）设计了一种采用3-RPS 并联机构作为执行部件支撑件的汽车车身制造与喷漆机器人，对该机器人和所设计的并联机构进行了简要描述，基于螺旋理论分析了机构运动自由度。

2）对机构运动过程中的寄生运动进行了分析，建立了机构寄生运动方程并准确求解出寄生运动表达式，获取了动平台运动的完整位姿，利用机构支链闭环方程建立了整个机构的运动学方程。

3）利用MATLAB 和Admas View 软件分别完成了运动学方程求解和运动学仿真，两者结果误差在3%以内，证明所建立的设计机构运动学方程有效可行，可以进一步用于机器人的控制设计与路径规划。