基于弹性秘密共享的多方洗牌协议
满子琪 张艳硕 严梓洋 罗乐琦 陈 颖
(北京电子科技学院 北京 100070)
数据隐私保护[1]问题已成为学术界关注的热点.洗牌协议[2]是旨在实现安全随机排列的协议,其将输入的数据打乱以保证数据隐私.秘密共享技术[3]是一种秘密保护技术,其将秘密份额分发并设置恢复秘密的门限值.
基于弹性秘密共享的多方洗牌协议的主要思想为:弹性秘密共享技术将数据集拆分成多个份额,洗牌协议对份额混淆处理.只有同时拥有一定份额的参与者才能够还原出原始数据.最后通过隐私交集计算,在参与者拥有数据集的交集达到了门限值后才能完成秘密的恢复.在此过程中,任何参与者都无法得知其他参与者所持有的数据,保证了数据的隐私性.
本文的主要创新点如下:1)引入了弹性秘密共享,增加了洗牌协议的容错性以及抗合谋攻击性;2)设计出一种多方下简单且效率较高的洗牌协议,具有较好的应用性;3)将洗牌协议和隐私集合交集计算技术相结合完成秘密的恢复,提高了恢复过程的隐私性.
1 相关工作
1.1 弹性秘密共享
秘密共享最早由Shamir[4]于1979年提出,并于1986年[5]提出了(t,n)门限方案.Desmedt等人[6]于1991年提出了弹性秘密共享的概念.弹性秘密共享保证了存在一定数量恶意参与者的情况下方案的可靠性.Roy等人[7]于2014年提出了一种防止作弊行为的秘密共享方案.肖健等人[8]于2023年提出了一种基于多答案保护的弹性秘密共享协议.
与秘密共享相比,弹性秘密共享具有可恢复性强、安全性好、可扩展性强等优点.因此,本文创新地在洗牌协议中引入了弹性秘密共享,较之传统的基于秘密共享的洗牌协议,本文协议具有更高的安全性与可扩展性.
1.2 洗牌协议
洗牌协议主要用于对数据进行随机排序,最初由Chaum[9]于1981年提出.Chen等人[10]于2020年提出了一种基于秘密共享和洗牌的数据发布协议.Melissa等人[11]于2020年提出将加密的元素和位向量进行洗牌.粟勇等人[12]于2022年提出了一种基于安全洗牌和差分隐私的联邦学习模型安全防护方法.
洗牌的特点在于其随机性.数据集中的每组数据在洗牌后都等概率地出现在空间的各个位置,有效地降低了攻击者找到某一特定元素进而展开攻击的风险.
1.3 基于秘密共享的洗牌协议
2000年,Cramer等人[13]提出将洗牌协议和秘密共享相结合,但并未给出详细的过程.2001年,Damgard等人[14]提出一种基于秘密共享的洗牌协议,主要特点是能够实现公开验证和保密性.但是,其对参与者的诚实性有较高要求.Pinkas等人[15]于2012年提出一种基于洗牌协议的安全多方计算协议,并提高了计算的效率和可扩展性.Kong等人[16]于2021年提出一种随机化洗牌技术,用于保护参与者在协作学习过程中的隐私.
1.4 隐私集合交集计算
隐私集合交集计算[17]能够在计算参与者私有数据集交集的同时,不泄露除交集以外的其他信息.
Meadows[18]于1986年提出首个隐私集合交集计算协议.随后,Huberman等人[19]于1999年对Meadows[18]的方案作出了细致的描述.Freedman等人[20]于2004年基于不经意多项式求值构造了隐私集合交集计算协议.申立艳等人[21]于2017年对两方隐私集合交集计算协议进行了简要总结.高莹等人[22]于2023年对基于多个参与者的隐私集合交集进行了综述.
1.5 布隆过滤器
布隆过滤器是一种集合元素查询工具[23],用来确定一个元素是否为集合的成员.Bloom[24]于1970年首次提出布隆过滤器,其主要功能是查询元素是否属于某集合.布隆过滤器可以看作将元素编码在一个长度为m的数组中.通过使用哈希函数和位向量,对元素的哈希映射位置来间接存储元素.
2 基于弹性秘密共享的多方洗牌协议的设计
2.1 整体思路
弹性秘密共享算法可以保证数据的机密性,确保数据不被恶意泄露.洗牌协议可以对数据进行重新排列,从而保护数据的隐私.
数据拥有者可以使用弹性秘密共享算法对数据进行共享,然后使用洗牌协议对数据进行重新排列,即使参与者窃取了部分密文也无法推断出原始数据的内容.因此,将弹性秘密共享和洗牌协议相结合可以在保护数据隐私的同时保证数据的机密性和完整性.
2.2 详细步骤
本文提出了一种基于弹性秘密共享的多方洗牌协议.假设本文采用的弹性秘密共享技术基于(t,n)门限,协议参与方的个数为n,参与方拥有的集合为X,每个集合的比特长度为a.本文所用的相关符号如表1所示:

表1 相关符号说明
该协议的具体流程如下:
1) 秘密份额的生成算法.
分发者选定一个秘密s,随机性地选择n个不同的索引作为相应的自变量{a1,a2,…,an}.
根据这些索引选择一个最高次幂为t-1的秘密多项式f(x),满足条件f(0)=s.
秘密份额的集合为{s1,s2,…,sn},且满足条件si=f(ai).
2) 数据集的洗牌.
生成秘密份额后将这些秘密份额打乱顺序,将秘密份额看作元素,并将这些元素组成长度为N×n的数组.
从末端元素开始向前遍历数组.
直到第2个元素,对于每个位置i,随机生成一个范围在[0,i]之间的整数j.
接着将第i个位置的元素与第j个位置的元素交换.
然后继续向前遍历数组,重复前2段步骤,直到遍历到第1个元素为止.
最后,打乱后的数组即为随机打乱后的顺序.
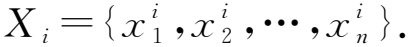
每个参与者只能看到自己所持有的数据部分,而无法看到其他参与者的数据.每个参与者可按照上述对其所持有的秘密共享数据部分进行洗牌.
3) 布隆过滤器生成算法.
假设一共有k个哈希函数.任意选择1个参与方,如P1.P1用自己的份额构造长度为m的布隆过滤器.具体算法如下:
首先P1用哈希函数将自己的每个元素都进行仿射变换,得到n个因变量.
然后将这n个因变量作为布隆过滤器数组的自变量,并为每个因变量赋相应的随机种子,这样就实现了将弹性秘密共享生成的秘密份额分别放在自己集合元素映射到布隆过滤器位置的过程.
当插入1个元素到布隆过滤器中时,k个不同的哈希函数分别对该元素进行映射,所得到的k个结果的异或仍然为该元素.
同时,P1将该混淆布隆过滤器分解为n-1个子混淆布隆过滤器,满足分解后的n-1个子混淆布隆过滤器的异或为原混淆布隆管理器.
随后P1将n-1个子混淆布隆过滤器发给其余的参与方P2.
4) 份额收发.
在份额收发阶段,参与者之间需要相互交换它们的份额,以便进行后续的计算操作.
通过异或秘密共享方案隐藏各个参与方的混淆布隆过滤器.
具体为:P2,P3,…,Pn运行1个异或秘密共享方案,并公开各自的秘密份额异或后的结果.每个参与方根据自己的秘密份额生成自己的布隆过滤器,并由此构造混淆布隆过滤器.
5) 交集计算.
利用弹性秘密共享能否重构出秘密判断交集基数是否达到门限值.如果能达到重构值,即:交集数量达到门限值,则能够输出共享的秘密;否则,可以推断出交集数量没有达到门限值,协议终止.具体算法流程如下:
3 基于弹性秘密共享的多方洗牌协议的分析
3.1 正确性分析
如果交集数量达到门限值则能够输出共享的秘密;否则,可以推断出交集数量没有达到门限值,协议终止.
定理1.本文协议采用的弹性秘密共享满足正确性.
当参与方P1,P2,…,Pn交集数量达到门限值t时,可以获得足够多的正确份额重构秘密s.弹性秘密共享能够重构秘密需要满足如下条件:
参与方元素的交集≥t+(n+d-t)/2.
这里的d为冗余码的数量,n为参与方的集合元素的大小.引入冗余码后,需要满足
t+d=t+(n+d-t)/2,
因此d≥n+t.
因此协议的离线阶段通过相同的随机种子生成n-t个相同的伪元素.
当1个元素x是交集中的元素时P1通过元素x查询混淆布隆过滤器可以得到.
因此,当交集数量达到门限值t时,可以获得足够多的秘密份额重构秘密s.本文提出的协议可以保证正确性.
定理2.本文协议采用的洗牌算法满足正确性.
证明.洗牌算法的方法是通过数学归纳法,考虑洗牌算法在每次迭代中是否能够产生1个等概率的排列.
假设在第i步之前已经产生了1个等概率的排列.
在第i步中,从剩余的元素中随机选择1个元素,并将其与第i个元素交换.这将生成另一个等概率的排列,因为每个元素都有相同的概率成为第i个元素.
当算法完成时将得到一个由原序列中的元素组成的等概率排列,因为每次都是从剩余的元素中随机选择1个元素来交换,而不是从已经交换过的元素中选择.
因此,该洗牌算法的正确性可以得到证明:如果使用一个公平的随机数生成器,那么该算法将产生一个等概率的排列.
证毕.
定理3.本文协议采用的布隆过滤器假阳性可能性很低,其潜在的误差可以忽略不计.
假设需要处理的集合为{x1,x2,…,xn},存在k个m位的哈希函数.哈希函数将每个元素独立且均匀地映射为随机数.这是一个乐观的假设,适合于实际实现.在这个假设下,在s的所有元素被散列到布隆过滤器后,某个特定位仍然为0的概率:
p′=(1-1/m)kn≈e-kn/m,
所以为了方便性,可以用p=e-kn/m来代替p′,则在p的前提条件下,假阳性的概率f为
f=(1-p)k≈(1-p′)k=(1-e-kn/m)k,
这个概率是很小的,故本文协议采用的布隆过滤器假阳性可能性很低,其潜在的误差可忽略不计.
3.2 安全性分析
定理4.本文协议在半诚实模型中是安全的,可以抵抗合谋攻击.
假设参与方pk是攻击者,那么其进行如下攻击操作:
首先选择一个随机值rand1和2n-t个自变量a1,a2,…,a2n-t,结合相应的因变量计算布隆过滤器Bk,并将其拆分为n-1份.
然后攻击者Pk根据布隆过滤器Bk和交集I随机且独立地对布隆过滤器SBk进行采样.最终,攻击者Pk可以得到的信息为攻击者Pk享有的秘密份额xk、交集I以及布隆过滤器SBk.
然而攻击者Pk无法计算其余参与方的布隆过滤器,因为没有其余参与方的秘密份额,同时也无法区别真实执行的和随机生成的布隆过滤器.
在合谋攻击中,攻击者企图获取秘密s.诚实的参与者发送布隆过滤器给攻击方后.布隆过滤器SBi是参与者Pi通过对布隆过滤器Bi和随机数异或得到的.
由于秘密共享保证了随机数和布隆过滤器的安全性.攻击者无法区别真实执行的和随机生成的布隆过滤器.所以攻击者无法得到其余参与者的隐私信息,也无法确定协议真实的算法.故本文协议可以抵御合谋攻击.
3.3 对比分析
本文协议还与其他基于秘密共享的洗牌协议进行了对比,具体如表2所示.

表2 本文协议与其他方案对比
本文协议所采用的洗牌算法的基本思想是从数组中随机选择1个元素,然后将它与数组的最后1个元素交换位置,依此类推,直到数组的第1个元素.因此洗牌算法的计算复杂度是线性的,即O(n).本文协议在生成布隆过滤器时的计算复杂度为O(nk),各方计算其布隆过滤器的计算复杂度与布隆过滤器的长度相关,为O(m).在秘密共享的重构阶段,计算复杂度为O(nlogn).总体来说,本文协议的计算复杂度为O(n+nk+m+nlogn).
Cristofaro[26]提出了一种基于秘密共享的洗牌协议.该协议确保在洗牌过程中每个服务器和客户端都只了解到洗牌结果的一部分.该方案具有较高的效率,但不能较好地抵御合谋攻击.其构建哈希链的时间复杂度O(n),其中n是原始数据的大小.而哈希函数近似于O(1)的计算复杂度.故哈希链洗牌的计算复杂度为O(n+1).
Huang等人[25]提出了一种基于安全多方计算的洗牌协议.该协议允许参与方将其私有数据进行洗牌,可以抗合谋攻击,但是在参与方数量增加时,计算复杂度会大幅度增加.该协议采用的洗牌算法的计算复杂度为O(n2),因为每次选择和移除元素都需要线性时间.此外,该方法通常需要额外的空间存储新的随机排列数组.
4 应用前景分析
4.1 具体应用
本文提出的基于弹性秘密共享的洗牌协议在数据隐私保护方面具有一定的实用性,包括但不限于如下方面:
1) 弹性秘密共享和洗牌双重保护数据共享.秘密共享协议将秘密分配给不同的参与方,洗牌协议随机重组数据,以保护数据的隐私.解密需要各方协同重组消息.这种方案在医疗、金融等领域得到广泛应用.
2) 协议支持多方下的安全计算.将参与方的数据进行随机混淆和重组,并使用秘密共享协议将其分配给不同的参与方.最后,各方协同解密并重组数据.这种协议广泛应用于机器学习等领域.
3) 协议应用于检索和排序.将检索和排序任务分配给多个参与方,各方将其拥有的数据进行洗牌处理,并使用秘密共享协议将其分配给其他参与方.
4.2 存在的问题
本文协议目前存在的一些问题主要有:
1) 秘密共享的计算复杂度略高.协议需要对数据进行多次处理,因此会增加数据处理的时间成本.
2) 隐私交集计算的通信开销可进一步降低.洗牌协议和秘密共享需要对数据进行多次传输,因此会增加数据通信开销.
3) 协议应用受到参与方个数的限制.洗牌协议和秘密共享需要多个参与方进行协同处理,因此会限制其在大规模数据处理中的应用.
5 结 语
本文提出一种基于弹性秘密共享的多方洗牌协议,充分利用了弹性秘密共享、洗牌协议等相关的密码学技术.通过与相关协议对比,本文协议兼具实用性和安全性等特点,能够很好地保护用户数据隐私,有较好的应用前景.

