基于科技项目评审专家异质性的共识测度方法

李 山，王 俊，赵旭东

（1.华东交通大学经济管理学院，江西南昌 330013；2.江西新型智库数据中心，江西南昌 330013）

0 引言

现行同行评议制度下，非共识项目由于其风险性与同行评议制度的不相适应，导致此类项目大量落选［1-2］。非共识项目所蕴含的重大创新是现代科学发展所必需的元素，近现代科学许多重大发现与突破都发源于蕴藏着潜在机遇的非共识项目［3］。因此非共识项目的再挖掘就显得尤为重要［4］。对于非共识项目的再挖掘，首先就是推荐合适的专家组［5］，若仅依据现有专家推荐要素即专家研究方向、学术关系等遴选专家［6-7］，专家的评审认知依旧可能会导致非共识现象大量存在［8］。共识度反映的是专家组评审总体认知，共识度越高，越利于非共识项目的再挖掘［9］，因此，若要为非共识项目的再挖掘推荐合适的专家组，有必要引入评审专家群体共识度测算。国内外共识度的相关研究倾向于偏好相似程度的度量和集结［10］，集中于OWA 算子、模糊语义量化等方法［11］。在项目评审领域，暂未出现专家评审共识度计算的相关文献，因此本文利用科技项目同行评议数据，结合历史评审数据与专家知识计算共识度，充分考虑专家历史信息与当下信息，在保证相对客观的同时，也能反映专家的主观偏好信息。本文提出的共识度测算方法具体过程是以2020 年某科研类科技项目评审数据为研究对象，评审专家有着丰富的学术背景，存在大量公开发表的论文等数据可以作为专家知识度量的依据。因此，首先通过这些学术型评审专家历史评审数据［12］构建的专家先验权重，结合反映专家异质性的主题覆盖度和权威度［13］确定的专家后验权重，得到最终的专家权重，再利用互反矩阵共识决策算法［14］11计算专家评审结果的共识方案排序，并利用排名偏差重叠计算每位专家的评审共识度。

1 文献综述

大群体决策共识过程是指决策群体通过讨论或其他方式协调不同意见与看法，达成某种意义上的一致，最终做出决策［15］，此过程主要包含群体共识度的测度以及非共识的修正两个步骤［16-17］。科技项目评审亦属群体决策，对于难以做出决策的非共识项目，则需要为其推荐合适的专家组对其进行再挖掘［18-19］。现有专家遴选标准主要包括专家权威度、专家知识结构、主题匹配度、专家学术关系网等［20］，若依旧按照现有标准遴选专家，评审专家的主观认知和偏好依旧会导致非共识现象的产生［21］。共识度反映的是专家组评审偏好的一致性，共识度越高，越利于挖掘出有价值的非共识项目［9］，因此针对非共识项目的评审专家推荐，需要引入反映专家评审偏好的共识度。但由于群体内的异质性难以量化，共识度的难以测度直接对决策环境的共识进程产生影响，因此，共识度的测度一直是研究热点［22］。现有研究主要集中于偏好相似程度的度量和集结中［10］。在偏好相似程度的度量方面，Liu 等［23］依据曼哈顿距离计算偏好相似度；Wu 等［24］提出度量偏好相似程度的重要依据之一是个体评价的传递性特征；王运等［25］融合用户与物品之间关系提出了偏好相似度的概率矩阵分解推荐算法；Wang 等［26］和Zhang等［27］都利用了规划模型测度并改进个体评价中的偏好相似程度。在偏好关系的集结方面，OWA 算子是最经典的集结模型［28］；Liu 等［11］依据决策者自信程度集结偏好关系；罗世华等［29］提出一种改进的Choquet Bonferroni 算子，将偏好关系转化为决策者权重后再集结；Del 等［30］通过测算不同集结方式对群体共识度的影响，提出了基于有序集结算子的集结模型。根据上述研究，发现群体共识度测算存在以下不足：一方面，现有文献对科技项目评审共识度的关注较少；另一方面，专家的异质性在测算中并未得以区分，如专家研究方向、权威度的差异极易导致共识度的计算产生偏差，且未考虑专家历史评审偏好。基于以上考虑，本文提出了一种结合历史信息与当下信息的共识度测算方法，选择某次科技项目专家评审数据为研究对象，结合此次评审专家的历史评审数据测度历史评审偏好，并结合专家研究背景知识计算此次评审活动的群体共识度。

在方法的选择上，群体共识是现代决策科学的重要组成部分，是目前决策领域的研究热点之一，国内外在共识模型、算法及其应用等方面具有深度研究［31］。吴志彬［14］11在《群体共识决策理论与方法》中阐述的基于互反矩阵的群体共识决策方法，不仅考虑了个体理性和群体理性，而且分别给出了个体一致性改进和群体共识达成的算法，具有良好的可调节性。因此本文选择互反矩阵共识决策用以计算依据专家评审数据达成的共识决策方案，但此方法在专家权重确定时主观赋予每位专家相同权重，专家的异质性并未得以体现。权重作为专家异质性的一种重要表达方式，一直都是群体决策领域的重点研究问题［32］，学者从很多方面对该问题展开了研究。易平涛等［12］根据数据聚类思想及信息集结方法、时间权向量的求解思路，给出了一种兼顾专家先验权重和后验权重的权重确定方法；赵千等［13］提出融合主题覆盖度和专家权威度的专家推荐框架，综合考虑覆盖度和权威度两种因素作为专家权重。本文为计算专家的异质性，首先借助易平涛等［12］人的研究提出的先验权重确定方法，以专家历史评审数据确定专家历史评审偏好作为先验权重；其次参考赵千等［13］人的研究提出的专家权重确定方法，结合专家研究方向与项目内容的相似度、权威度作为后验权重；最后结合先验权重与后验权重得到最终专家权重。此权重确定方法同时兼顾专家历史信息和当下信息，并考虑了专家研究方向、权威度等极易导致共识度产生偏差的指标。由于后验权重的计算依赖于专家公开发文数据作为基础，因此本次研究对象针对的是科研类科技项目评审专家，这些专家均有丰富的学术背景，有着大量公开发表的论文，可以用于测度专家知识。确定专家权重后，以互反矩阵共识决策计算本次评审活动的共识决策方案，再利用Chen 等［33］提出的排名偏差重叠计算每位专家与共识决策方案的相似程度得到群体共识度。

2 问题描述与条件假设

本文要解决的问题是：一是决策者异质性权重的获取。在过往共识度的计算中，决策者异质性一直是难点之一，本文利用决策者背景数据，通过Word2Vec 词向量模型、Critic 法等方法测度异质性权重。二是共识度的获取。借助客观数据，通过互反矩阵共识决策模型获取共识决策方案，并对比各决策者方案，通过排名偏差重叠计算得到共识度。为了更准确地说明问题，现给出2 个假设：

（1）决策者均为本次评价活动专业相关领域的专家；

（2）各位专家的判断具有一定的稳定性。

3 基础知识

3.1 互反矩阵

3.2 个体一致性度量

根据吴志彬等［14］12关于个体一致性的度量标准，给出以下的定义。

则称A为具有满意一致性的互反矩阵。

3.3 共识程度度量

定义5：令A1,A2,,Am为m个互反矩阵。假设是由几何平均算子集结得到的群体互反矩阵。的群体共识一致性指标定义为

4 方法与基本原理

4.1 决策者权重的确定

m个决策者针对n个项目做决策，在决策过程中由于决策者之间研究方向、判断水平等知识存在差异，每位决策者以不同的方式解释评价指标，导致决策者最终决策未能达成共识。

4.1.1 决策者先验权重

通过历史评审数据来反映决策者的历史评审水平，并与最终评审结果对比［12］。具体过程如下：

（1）收集每位决策者历史评审数据，将每位决策者评审数据处理为表1 形式。

表1 决策者历史评审信息

（2）决策者历史序值相关系数的计算。本文采用斯皮尔曼等级相关系数对决策者在不同时期内的评审结果进行序值的相关系数计算，其计算公式为：

式（6）中：d表示序值之间的差距，j表示等级个数，序值一致性越高r越大。

（3）运用指数平滑推测本次评审中决策者的序值相关系数。一次指数平滑的公式为：

4.1.2 决策者后验权重

在评审过程中，由于决策者研究方向的影响，决策者对与自己研究方向相近的评审项目会有更清晰的判断，因此以主题覆盖度来反映该影响因素。同时，决策者权威度会导致决策的可信度产生偏差，因此选择将主题覆盖度与决策者权威度同时纳入专家权重的计算，并称之为后验权重。

（1）主题覆盖度。

利用决策者发文摘要与项目研究内容，通过Word2vec 词向量模型输出摘要-研究内容词对，计算余弦相似度，以此反映决策者研究方向与评审项目研究内容的相关程度，即主题覆盖度。具体步骤如下：

①将决策者发文摘要与评审项目研究内容去除停用词，切分成词的形式并导入语料库，处理成Word2vec 模型的训练格式。

②建立所有决策者的发文摘要与所有评审项目研究内容的Word2vec 词向量模型。

③通过余弦相似度对训练得到的摘要—研究内容词向量计算决策者发文摘要与评审项目研究内容的相似程度。余弦相似度的计算公式为：

④主题覆盖度权重计算公式为：

（2）决策者权威度。

决策者权威度的计算需要利用决策者论文发表量、h 指数、被引量等指标信息，通过critic 权重法对决策者权重进行计算。具体步骤如下：

①获取决策者论文发表量、h 指数、被引量等指标信息，并处理为critic 权重法所需的数据类型。

②对各指标归一化处理。正向指标的做法为：

负向指标的做法为：

③变异性的处理。在critic 权重法中利用标准差表示变异性，变异性较大的决策者信息，反映出更多信息，应赋予更高的权重。变异性的计算公式为：

④冲突性。决策者之间的相关系数越大，冲突性就越小，权重也越小。critic 权重法中使用相关系数的形式反映相关性，计算公式为：

⑤信息量越大的决策者应被赋予更高的权重，信息量的计算公式为：

⑥权重的确定。

（3）后验权重的确定

第q位决策者后验权重为：

4.1.3 决策者最终权重

在本次评审中，决策者最终权重为

4.2 互反矩阵共识决策

互反矩阵共识决策是在同时考虑个体理性与群体理性的情况下，给出个体一致性改进和群体共识达成的算法，一共分为个体一致性控制阶段、共识达成阶段、方案排序阶段3 个阶段［14］14。

4.2.1 个体一致性控制算法

算法1：互反矩阵的个体一致性改进。

个体一致性控制阶段的具体过程。

（1）根据定义1，从各决策者对项目的决策数据中，提取出m位决策者初始偏好信息A1,A2,,Am；

4.2.2 共识达成算法

算法2：基于互反矩阵的共识达成过程。

个体一致性控制阶段实现后，共识达成阶段的过程如下：

4.2.3 方案排序

4.3 共识程度的获取

获取排序列表后，借助排名偏差重叠（rank biased overlap，RBO）计算每个决策个体的排序列表与群体的共识程度［33］，计算步骤如下：

假设S为决策个体的排序列表，T为群体互反矩阵对应的排序列表。为列表S的第i个元素，表示列表中从位置c到位置d所有元素组成的集合。在深度为d时，列表S和T的交集为：

交集的元素个数相对于深度d的比值称为列表S和T的一致度，再赋予每个深度的一致度权重,得到相似度：

因此，设定参数p，排名偏差重叠（RBO）距离度量方法可以简化为

RBO 指标范围在［0,1］之间，值越接近1 表示列表之间共识程度越高。

5 应用算例

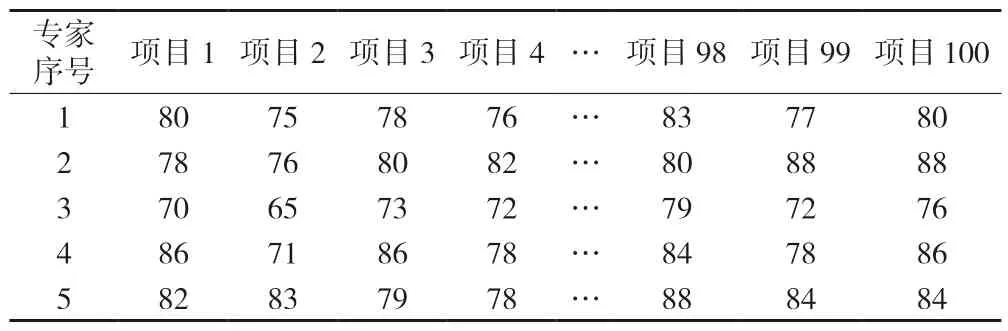
表2 专家评分 单位：分

5.1 专家权重的确定

5.1.1 专家先验权重的确定

5 位学术型专家的先验权重计算结果为

表3 专家评审数据 单位：分

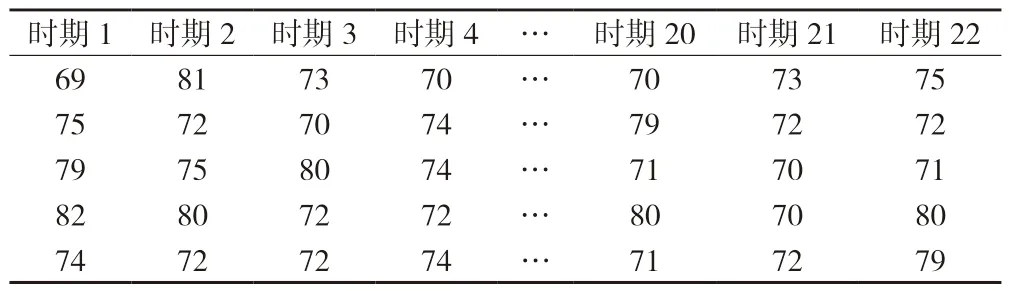
表3 专家评审数据 单位：分

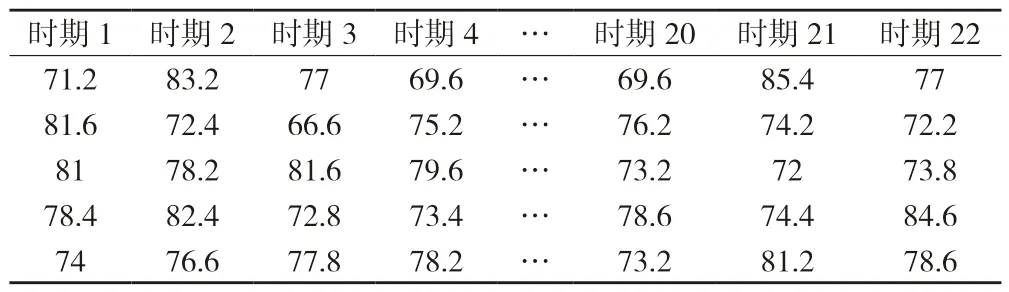
表4 专家群最终评审数据 单位：分

表5 专家序值信息

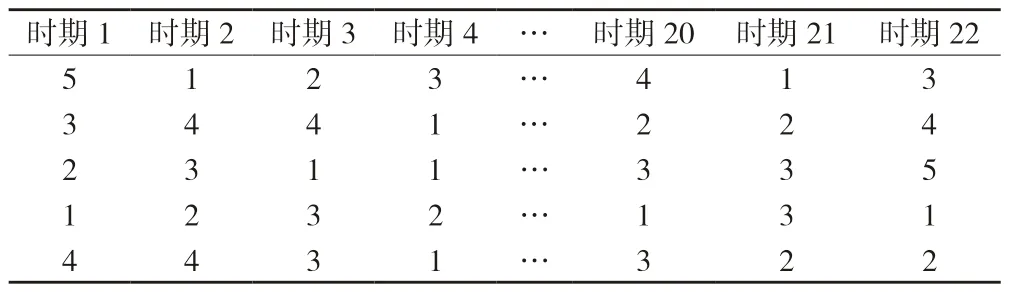
表5 专家序值信息

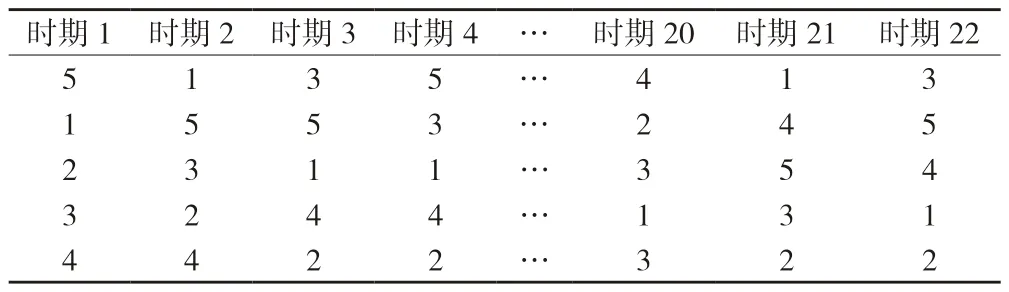
表6 专家群序值信息

表7 专家序值相关系数表

表7 专家序值相关系数表

5.1.2 专家后验权重的确定

（1）主题覆盖度

主题覆盖度反映的是每位学术型专家所有发文摘要与评审项目研究内容的余弦相似度，根据4.1.2主题覆盖度的计算过程所述得到结果为

计算过程如下：

①收集每位专家所有发文摘要与评审项目的研究主题，利用Python 的jieba 库将其分词后，再加载停用词，去除停用词后导入语料库中。

②利用每位专家发文摘要的语料库，结合评审项目研究主题的语料库训练Word2vec 模型，训练出5 位专家的Word2vec 词向量模型。

③定义余弦相似度求取函数，并利用5 位专家的Word2vec 词向量模型求取每位专家的余弦相似度，结果为

④主题覆盖度权重的确定。5 位学术型专家主题覆盖度权重为

（2）专家权威度

专家判断的差异对于项目评审的影响是毋庸置疑的，本文利用学术型专家权威度反映专家判断水平，所使用的指标包括专家学位、评审年份、参与评审的课题、论文发表量、著作数量、h 指数、被引量等指标数据，通过critic 权重法对学术型专家赋权，根据4.1.2 决策者权威度的计算过程所述得到结果为

计算步骤如下：

①获取5 位学术型专家学位、评审年份、参与评审的课题、论文发表量、著作数量、h 指数、被引量等指标信息，并将其处理为critic 权重法所需的数据类型。

②由于指标特征值都有含义，因此不需要对负向指标、正向指标标准化，每位专家的变异性为

③计算冲突性。冲突性相关系数为

④计算信息载量。5 位专家的信息载量是

⑤根据信息载量获得5 位专家权威度权重分别为

（3）后验权重的确定

根据公式（18），由于主题覆盖度与专家权威度对项目评审的影响都不可忽视，因此本次取0.5，最后求得专家后验权重为

5.1.3 专家最终权重

5.2 互反矩阵共识决策

确定专家权重后，为方便进行基于互反矩阵的共识决策，需要将每位专家当期100 个评审项目的评分数据转化为互反矩阵。本文将每位专家评分的极差九等分，得到定义1 中的互反矩阵，根据专家一的评分数据转化为的互反矩阵如表8 所示。得到5 位专家的互反矩阵后，即可按照基于互反矩阵的决策支持模型来获取专家决策共识情况。

表8 专家一互反矩阵

表8 专家一互反矩阵

5.2.1 个体一致性控制阶段

计算5 位专家的初始一致性指标，由于数据量较大，计算过程均通过Python 实现，此处仅列出计算结果。步骤如下：

（1）群体互反矩阵Ac的构造。根据5 位专家的权重

结合定义2 构造的群体互反矩阵如表9 所示。

表9 群体互反矩阵

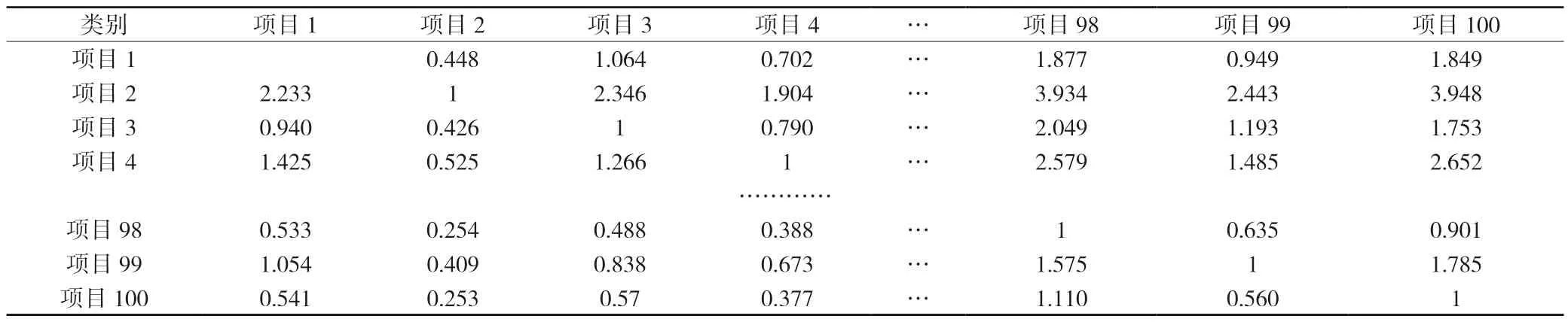
表9 群体互反矩阵

（2）一致性指标矩阵的构造。根据定义3，对5 位专家的互反矩阵A1,A2,A3,A4,A5以及Ac分别构造出含一致性指标的矩阵，根据专家一互反矩阵构造的如表10 所示。

表10 矩阵

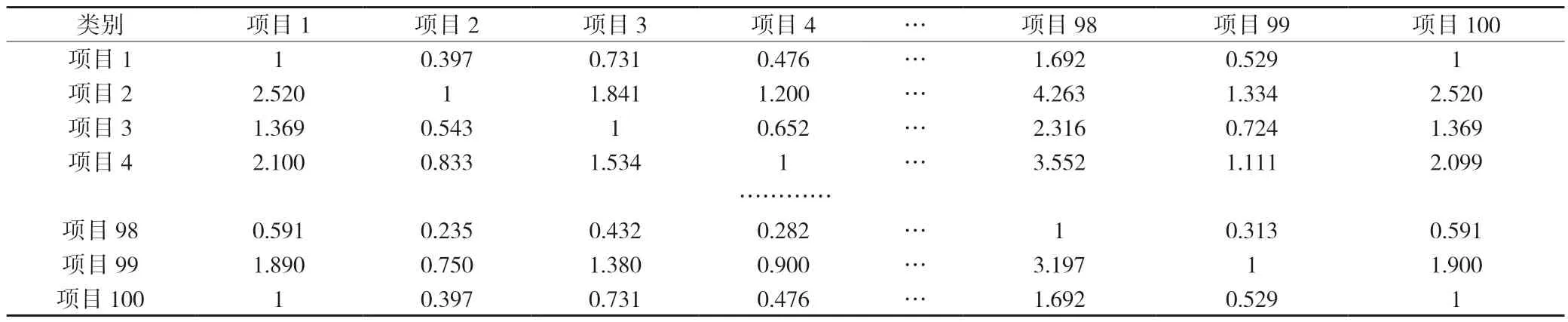
表10 矩阵

5.2.2 共识达成阶段

每位专家的共识一致性指标值的计算及修正步骤如下：

（1）群体共识指标GCIH(A)的计算。根据定义5，5 位专家的互反矩阵A1,A2,A3,A4,A5结合群体互反矩阵得到群体共识指标为

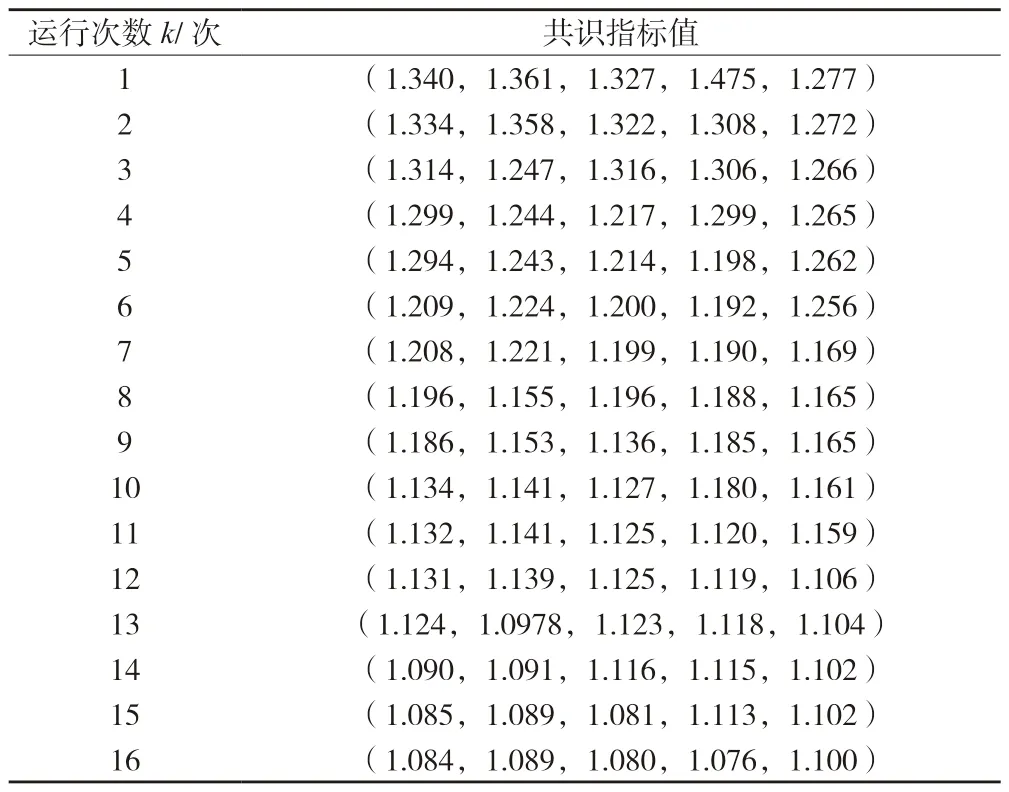
表11 共识指标修正过程

表12 处理后的群体互反矩阵

表12 处理后的群体互反矩阵

经过17 次迭代之后，修正后的群体一致性指标值为

5.2.3 方案排序阶段

图1 的排序

图2 专家的排序

图3 专家的排序

图4 专家的排序

图5 专家A4的排序

图6 专家的排序

5.3 共识度计算

得到排序列表后，将每位专家的排序列表与共识达成后的排序列表进行对比，设置p值为0.9，按照RBO 算法计算得到共识度为

5.4 对比分析

为展示本文方法的可行性与合理性，本文选择基于决策者一致性水平、群体共识度水平两方面数据与传统共识决策模型进行效果对比，具体过程是用传统共识决策模型计算本文案例的共识决策方案。

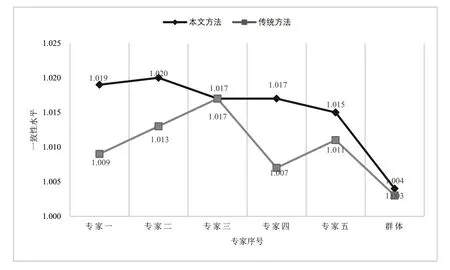
图7 决策者性水平对比

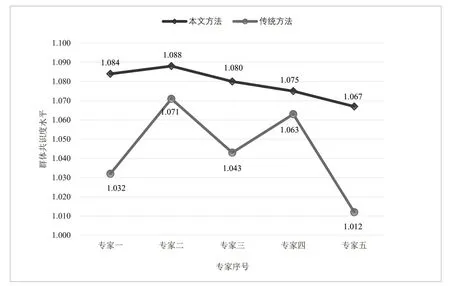
图8 群体共识度水平对比

综上所述，本文对于科研类科技项目评审的学术型专家共识测度方法充分考虑了历史信息和当下信息，充分挖掘了专家异质性的测度，计算过程中加入专家历史评审偏好、主题覆盖度、专家权威度等易对共识度计算产生影响的异质性指标，均以客观数据信息为依据，减少了主观信息的影响，使得整体结果在个体一致性水平和群体共识度水平上均有一定程度的提升，相比传统的共识决策模型有更好的适用性和灵活性。

6 结论

迄今，已有研究证明可对偏好相似程度进行度量和集结，但对于专家之间的异质性考虑较少，且鲜见利用评审数据测度专家共识的文献。本文提出的专家共识测度方法特点是利用科技项目评审数据、专家知识，考虑专家历史评审偏好的差异，结合主题覆盖度与专家权威度体现专家之间的异质性，进而通过互反矩阵共识决策模型计算专家共识度。从问题解决效果来看，本文设计的研究思路及决策步骤，充分考虑了影响决策进程达成共识的因素——专家异质性，解决了科技评审专家的共识测度问题，为非共识项目的再挖掘做好了铺垫。由于本次研究对象主要是科研类科技项目的评审，评审专家学术背景丰富，均有发文作为数据分析的基础，忽略了缺少研究论文数据支持的技术型专家的共识测度问题，从而使得本研究存在一定的局限性。但这也是下一步研究工作的重点，即将非科研类科技项目评审专家间的共识度纳入评审专家推荐模型中，为非共识项目推荐合适的专家组进行再挖掘，以此提升科技项目评审的准确性与整体质量，推动科技项目研究水平的稳步发展。