如何解答高中数学立体几何题
徐璐


【摘要】数学作为高中阶段的一门基础学科,学习难度大,具有抽象性强的特点,要求学生具备较强的逻辑思维能力.立体几何是高中数学中的重要知识内容,是高考中的必考知识点.立体几何题目具有灵活性和多变性的特点.在解题过程中,不仅需要学生掌握好基础知识,还需要学生掌握一定的解题方法与技巧,快速找出解题思路,提高解题效率.本文分析高中数学立体几何解题策略.
【关键词】高中数学;立体几何;解题策略
立体几何是高中数学学习中的难点与重点,在立体几何问题解题中,需要具有较强的空间想象能力以及逻辑思维能力,因此,大多数学生认为立体几何问题比较难.在实际的立体几何解题中,有着很多的解题方法和技巧,能够帮助学生少走弯路,提高学生解题能力.作为数学教师,应当结合例题讲解解题方法,让学生掌握解题方法的具体应用.
1 利用分类讨论方法解题
在立体几何解题中,需要认真分析题目,理解出题目的,结合题意画出草图,利用分类讨论方法,保证问题解答的全面性.
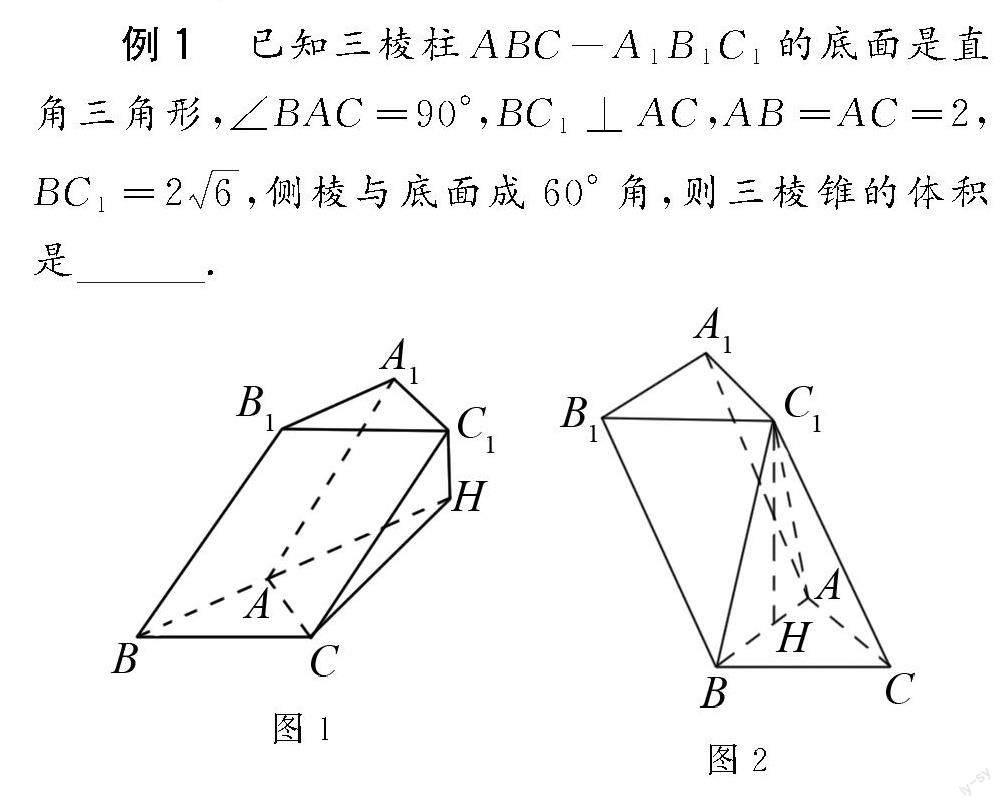
例1 已知三棱柱ABC-A1B1C1的底面是直角三角形,∠BAC=90°,BC1⊥AC,AB=AC=2,BC1=26,侧棱与底面成60°角,则三棱锥的体积是.
解 因为∠BAC=90°,
所以AC⊥AB,
因为BC1⊥AC,且AB与BC1存在共同点B,
所以AC⊥平面ABC1,所以平面ABC⊥平面ABC1.
因此,点C1在平面ABC上的射影在直线AB上,
过C1作C1H⊥AB,交点是H,设G1H=x,
(1)若点H在线段BA的延长线上,连接CH,
所以∠C1CH=60°,CH=33x,
在Rt△ACH中,AH=13x2-4,
在Rt△BC1H中,根据勾股定理解得x=15,
所以三棱柱的体积是15×12×2×2=215.
(2)若点H在线段AB上,在△BC1H中,根据勾股定理,x=26,即点H与点B重合,所以三棱柱的体积是46.
(3)若点H在线段AB的延长线上,在Rt△BC1H中,根据勾股定理解得x=26,不符合题意.
综上可知,三棱柱ABC-A1B1C1的体积是215或46.
2 利用向量法解答问题
在立体几何解题中,向量法是一种常用的解题方式.利用向量法构建相应的空间直角坐标系,将几何问题转化成代数问题,减少复杂的计算过程,帮助学生快速解决立体几何问题[1].
例2 如图3所示,立体图形ABCD-A1B1C1D1是一个底面为矩形的四棱台,平面AA1D1D⊥平面CC1D1D,且CC1=CD=D1D=12C1D1=1.
(1)证明:AD⊥平面CC1D1D;
(2)如果A1C与平面CC1D1D成的角是π3,求解二面角C-AA1-D的余弦值.
解 (1)如图4,作DH⊥C1D1于H,连接DC1,
因为CC1=CD=D1D=12C1D1=1,
所以D1H=12,则∠D1DH=30°,
所以DH=D1D·cos30°=32,
因为HC1=32,
所以DC1=DH2+HC21=3.
在△D1DC1中,因为D1D2+DC12=D1C21,
所以△D1DC1是直角三角形,且DC1⊥D1D,
因为平面AA1D1D⊥平面CC1D1D,且两个平面的交线为D1D,
所以DC1⊥平面AA1D1D,
因为AD平面AA1D1D,则AD⊥DC1,
因为AD⊥CD,DC∩DC1=D,
所以AD⊥平面CC1D1D.
(2)连接A1C1,以D1作为坐标原点,构建如图5所示的空间直角坐标系.
图5
因为A1D1⊥平面CC1D1D.
所以A1C1在平面CC1D1D的射影为D1C,
因为A1C与平面CC1D1D成的角是∠A1CD1=π3,
在Rt△A1CD1中,A1D1=3,
所以D1(0,0,0),A1(3,0,0),C0,32,32,
D0,12,32,C1=(0,2,0),
所以D1D=0,12, 32,D1A1=(3,0,0),
A1C1=(-3,2,0),
A1C=-3,32, 32,
设平面AA1D1D的法向量为m=(x,y,z),
所以m·D1D=0,m·D1A1=0,
所以12y+32z=0,3x=0,
令y=3,所以m=(0,3,-3).
设平面AA1C1C的法向量是n=(a,b,c),
所以n·A1C1=0,n·A1C=0,
所以-3a+2b=0,-3a+32b+32c=0,
令a=2,所以n=(2,3,3),
根据图5分析,二面角C-AA1-D是锐二面角,
所以cos
所以二面角C-AA1-D的余弦值是34.
3 结语
高中数学立体几何解题中,解题的方法有很多,需要學生掌握并且灵活利用,作为教师,讲解解题方法的同时,要求学生进行课堂总结,结合自身情况进行训练,体会解题方法的具体应用,从而提高学生的解题水平.
参考文献:
[1]王晨.高中数学立体几何高考试题解题分析[J].高中数理化,2019(16):1-2.
[2]王巧锋.浅谈高考数学中立体几何题的解题分析[J].中学数学(高中版),2021(03):79-80.
[3]王幼兰.高中数学立体几何高考试题分析与教学策略研究[J].考试周刊,2023(23):89-93.

