侧式进/出水口偏流出流下的大涡模拟
郭港归 刘亚坤 魏杰 曹泽 张帝
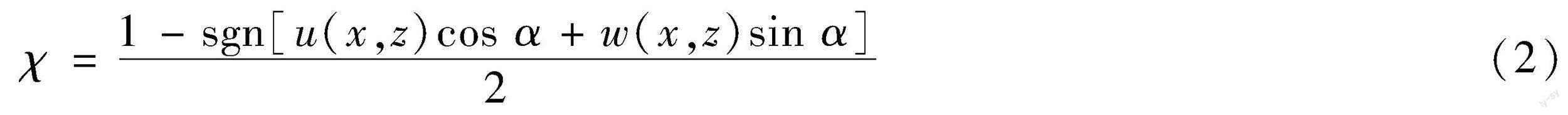
摘要:实际工程中受地形地质条件影响,引水洞在水平上存在转角,导致出流工况来流不均,进/出水口内部紊流特性的复杂程度显著提升。利用大涡模拟对某带水平弯段抽水蓄能电站侧式进/出水口进行数值计算,其流速、概率密度分布与模型试验吻合较好。结果表明:偏流出流下进/出水口各流道分流比分别为0.64、0.81、1.26和1.29,水平方向流速分布极为不均;垂直方向主流靠近中下部,垂向雷诺切应力在扩散段内呈一正一负峰值分布,该现象主要由中上部的流动分离和底部的壁面剪切造成;两中间流道的回流区高度大于两边流道,导致中间流道的拦污栅更易受到反向流速影响;流动分离使拦污栅附近存在三轴漩滚,靠近过水断面中上部和底部产生2处能量集中的低频脉动,且各流道在偏流条件下的紊动强度相比均匀来流的紊动强度分别提高11%、25%、29%、3%,不利的水流流态和较高的紊动强度可能对拦污栅造成威胁。
关键词:侧式进/出水口;偏流出流;雷诺切应力;流动分离;低频脉动
中图分类号:TV135 文献标志码:A 文章编号:1001-6791(2024)01-0132-13
抽水蓄能电站是一种清洁、环保、可持续的储能发电方式,目前在中国“双碳”的战略背景下迅速发展。进/出水口是抽水蓄能电站引水系统中的重要组成部分,其几何结构存在水平、垂直双向扩散,造成2个方向上均发生流动分离,三维流动特性明显,内部流场结构复杂、紊乱,需要重点关注。孙双科等[1]对抽水蓄能电站进/出水口进行模型试验,研究了不同断面的流速分布,发现隧洞坡度是造成各断面流速分布不佳的主要原因;王晨茜等[2]利用Realizable k-ε模型对进/出水口进行数值模拟,分析垂直扩散角对扩散段流动分离的影响,发现当垂直扩散角逐渐减小,流动分离减弱,该角度小于2°时,无明显流动分离现象;高学平等[3]利用粒子图像测速技术(PIV)对进/出水口出流工况内部流场进行测量,发现扩散段存在流动分离,顶部存在反向流速;朱洪涛等[4]采用激光多普勒流速仪得到隧洞段、扩散段、调整段和防涡梁段的紊动强度,发现紊动强度沿程先增大后减小;Ye等[5]采用数值模拟方法对进/出水口出流工况进行模拟,发现扩散段顶部出现大范围的回流区,其主要原因是主流在横向上扩散。大部分文献主要针对引水洞段为直线管道的进/出水口水力特性研究[6-7],而实际工程中由于地形地质的原因需要将引水洞设计为垂直或水平方向上偏转的体型。张兰丁[8]对带上弯段引水洞的响水涧抽水蓄能电站进/出水口进行试验研究,发现弯道效应将水流推向边壁;当过渡段长达到5倍隧洞洞径时,流速分布符合直管流动特性,弯道效应消失。张从联等[9]对惠州抽水蓄能電站进行模型试验研究,发现进/出水口与水平弯段之间直线洞段的长度需要大于40倍引水洞洞径才能满足各流道均匀分流的要求。实际上,水平弯段会使进/出水口在出流工况下的流道流量分配极为不均、流量偏向一侧,同时考虑扩散段造成水平和垂直方向上的流动分离,极可能使流道内部的流场更加紊乱,加剧水体质点的脉动。
由于国内缺乏对带水平弯段的侧式进/出水口紊流特性研究,且尤为关注偏流出流情况下拦污栅段的流场结构。本文以带水平弯段的某抽水蓄能电站上库侧式进/出水口为研究对象,利用大涡模拟方法对进/出水口进行模拟,分析水平及垂直方向的流速、雷诺切应力分布和进/出水口顶部回流区高度,并进一步研究拦污栅段的流场结构;从紊动能的角度分析进/出水口水头损失产生的源头,研究偏流出流下各流道不同断面的紊动强度分布并与均匀来流进行对比;对进/出水口各流道不同断面的流速测点做功率谱密度分析(PSD),研究流场涡旋结构在时间尺度上的分布。
1 研究方法
1.1 几何模型
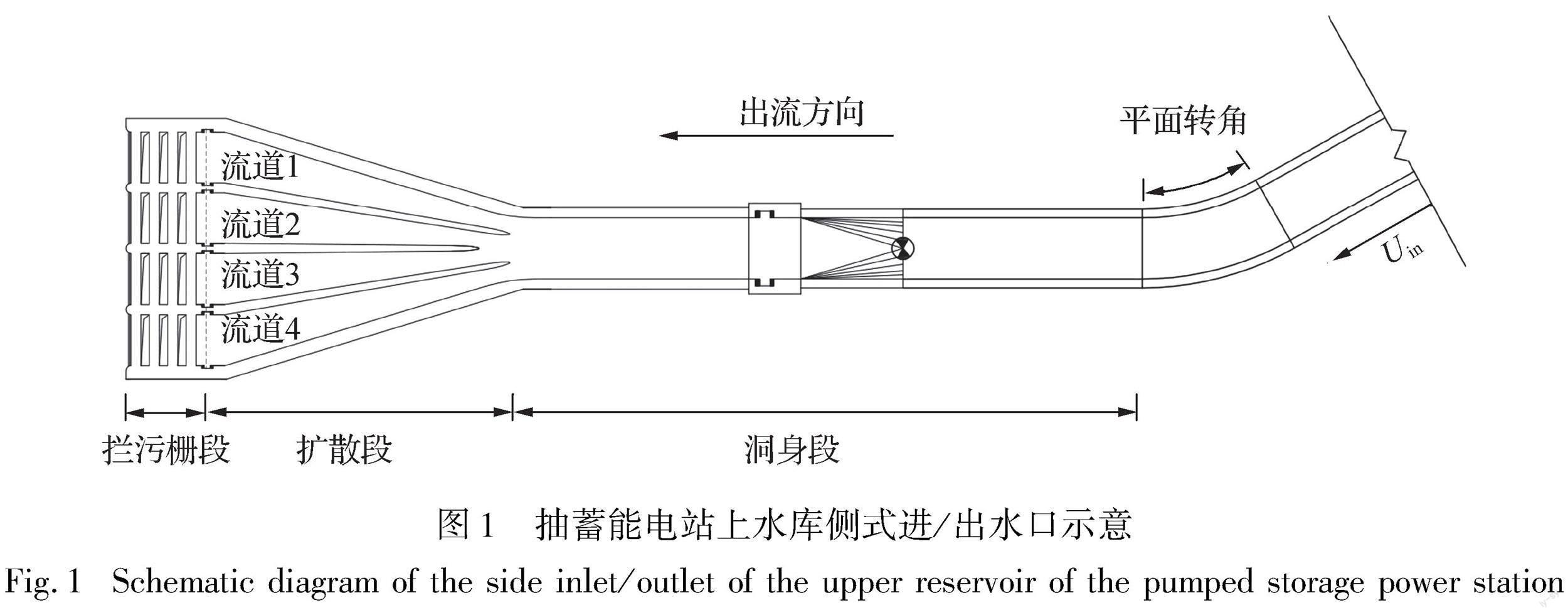
某抽水蓄能电站上水库侧式进/出水口模型试验示意如图1所示,采用三墩四流道布置,水平、垂向扩散角分别为33.774°、6.12°,Uin为隧洞断面的进口流速。在引水洞段存在平面偏转角,转角为29.27°,洞径为9 m,直线洞身段长约为洞径的17倍。模型试验比尺采用1∶40,进/出水口采用有机玻璃制作,4台机满发出流工况下流量为262 m3/s,各流道流速测点采用声学多普勒三维点式流速仪量测。
进/出水口网格如图2所示,采用混合网格计算,在扩散段和拦污栅段局部加密,第一层边界层为0.000 125 m,壁面处的y+(用于衡量近壁处湍流计算的精度是否足够)约1.0~3.5;内部水体为均匀的正方体网格,尺寸约0.004 m,边界层网格和正方体网格之间采用六棱柱网格过渡,尺寸与正方体网格一致,总网格量为600万。引水洞段采用结构化网格,总网格量约130万。
采用大涡模拟的方法[10-12]对进/出水口4台机组满发死水位出流工况进行模拟,隧洞断面采用流速进口边界,依据流量按平均流速给出,库区为压力出口边界,依据库水位按静压给出,库区顶部和检修门槽顶部为压力进口边界。亚格子模型为Smagorinsky-Lilly[13-14],并以动态计算[15]的方法调整Smagorinsky常数,压力耦合采用算子分裂的压力隐式算法(PISO算法),时间离散为有界二阶隐格式,空间离散采用二阶迎风格式,时间步长取0.005 s。
1.2 量纲一化处理与监测点布置
坐标、压强、流速以及流场二阶指标都经过量纲一化处理,从以往的研究[16-18]发现流速和长度分别以扩散段进口处时均流速(Ub)和宽度(H)进行量纲一化处理,本文Ub和H分别为3.22 m/s和9 m。坐标的量纲一化均以扩散段进口处的坐标为基准,以z方向为例,进/出水口各点的高程减去扩散段进口处底板的高程,再除以H,得到量纲一化的高程。
为获取水平、垂直方向的流速分布,沿水流方向取8个断面,x/H分别为-1.33、-2.06、-3.00、-4.40、-5.06、-5.44、-5.60、-6.10,称DM1—DM8。在每个流道中,沿8个断面中垂线上取垂向监测点,每条垂线布置11个监测点,如图3(a)所示,因此4个流道共32条监测线,总计352个垂向监测点;同理,在z/H=0.5的位置处取水平剖面,对8个断面沿水平方向取10个监测点,如图3(b)所示,总计320个监测点。最后,为了与模型试验流场进行对比,在拦污栅断面,即x/H=-5.6处,每个流道的左、中、右处分别布置5个监测点,4个流道总计60个监测点,用于验证数值模型结果的准确性。以上共732个监测点,每个监测点的采样频率为100 Hz。
1.3 模型验证
为了验证数值模型的有效性,对比了数值模型与物理模型的时均流场。表1为拦污栅断面中垂线处的流速分布,数值模型和物理模型在拦污栅断面时均流速分布较为接近,流道1—流道4的平均相对误差分别为10.9%、11.6%、4.0%和10.6%。
除了验证数值模型的时均流场外,还需要验证瞬时流场的准确性。湍流的主要特征是不规则性,其流速、压强的时间序列呈现不规则的振荡运动,属于随机过程,而在随机过程中,概率密度包含随机变量的全部统计信息[19]。因此,判断数值模型和物理模型的瞬时场是否一致可以通过验证某点瞬时流速的概率密度实现。取每个流道中垂线上的第3个测点进行概率密度验证,如图4所示,横坐标u+为标准化后的瞬时流速,发现各测点的物理模型和数值模型的概率密度较为接近,且基本符合标准正态分布;数值模型和物理模型的概率密度在峰值和均值存在一定差异,其主要原因是试验采用的测量仪器可能干扰内部流场,数值模型网格解析度不足造成脉动流速与实际存在差异。数值模型各测点的偏态系数(Cs)为0.44~0.70,峰态系数(Ce)为2.70~3.34。综上所述,本数值模型计算结果能够反映模型试验的时均和瞬时流场。
2 结果及分析
2.1 偏流出流下的流场分布
2.1.1 横向紊流结构
根据进/出水口的平面时均流速分布(图5)可知,偏流出流下流量主要集中在流道3、流道4,各流道分流比分別为0.64、0.81、1.26和1.29,流量分配极为不均;而均匀来流时流道2、流道3流量较大,各流道分流比分别为0.90、1.09、1.12和0.87。各流道主流核心区均靠近分流墩内壁,边流道和中间流道分别在x/H为-1、-2时出现流动分离。
图6为水平断面各流道的时均流速分布,横坐标代表在平面上该点与壁面的量纲一距离(L为沿y方向不同截面处的流道宽度)。均匀来流的水平流场结构与偏流来流下的结构相似,因此仅展现偏流的结果。图6中发现,各流道DM1的主流集中、流速达到最大,到DM3流动分离最明显,主流偏向内侧,在DM4之后流动分离减弱,流速分布逐渐均匀。除偏流出流下流道3的流速在DM4—DM8呈双峰分布以外,其他各流道断面流速分布均呈单峰分布,仅在流速的数值上存在差异。
雷诺切应力是一个重要的紊流指标,代表了流体质点的脉动动量通量,它将动能从高流速区再分配到低流速区域,实现动量交换[20],其公式如下:
式中:ρ为水的密度;u′、v′和w′分别为x、y和z方向的脉动流速。偏流出流和均匀出流下大部分流道的水平方向雷诺切应力分布相似,只有偏流出流下流道3的雷诺切应力分布存在差异,因此为避免重复仅展示偏流出流下流道3、流道4的雷诺切应力分布。如图7所示,DM1位于分流墩处,流道面积收缩,水流质点受到挤压,此时该断面各点的雷诺切应力几乎为0,流层之间脉动动量交换极少;沿着水流方向,在扩散角的影响下发生流动分离,雷诺切应力逐渐增大,在DM3达到最大;DM4之后的雷诺切应力沿程逐渐降低。与其他流道雷诺切应力呈单峰值相比,偏流出流下流道3的雷诺切应力分布在DM4—DM8呈现出一正一负双峰值分布,在文献[12]中的有压扩散器也发现类似的现象。流道3的水平流场远比有压扩散器复杂,偏流对其流场结构影响较大,此外还受到分流墩和垂直扩散角的约束,造成该流道DM4之后两侧的流速高、中间低,从而在高流速和低流速区的相互剪切下导致流道3在y/L=0.2~0.8之间形成一正一负的雷诺切应力分布。
2.1.2 垂向紊流结构
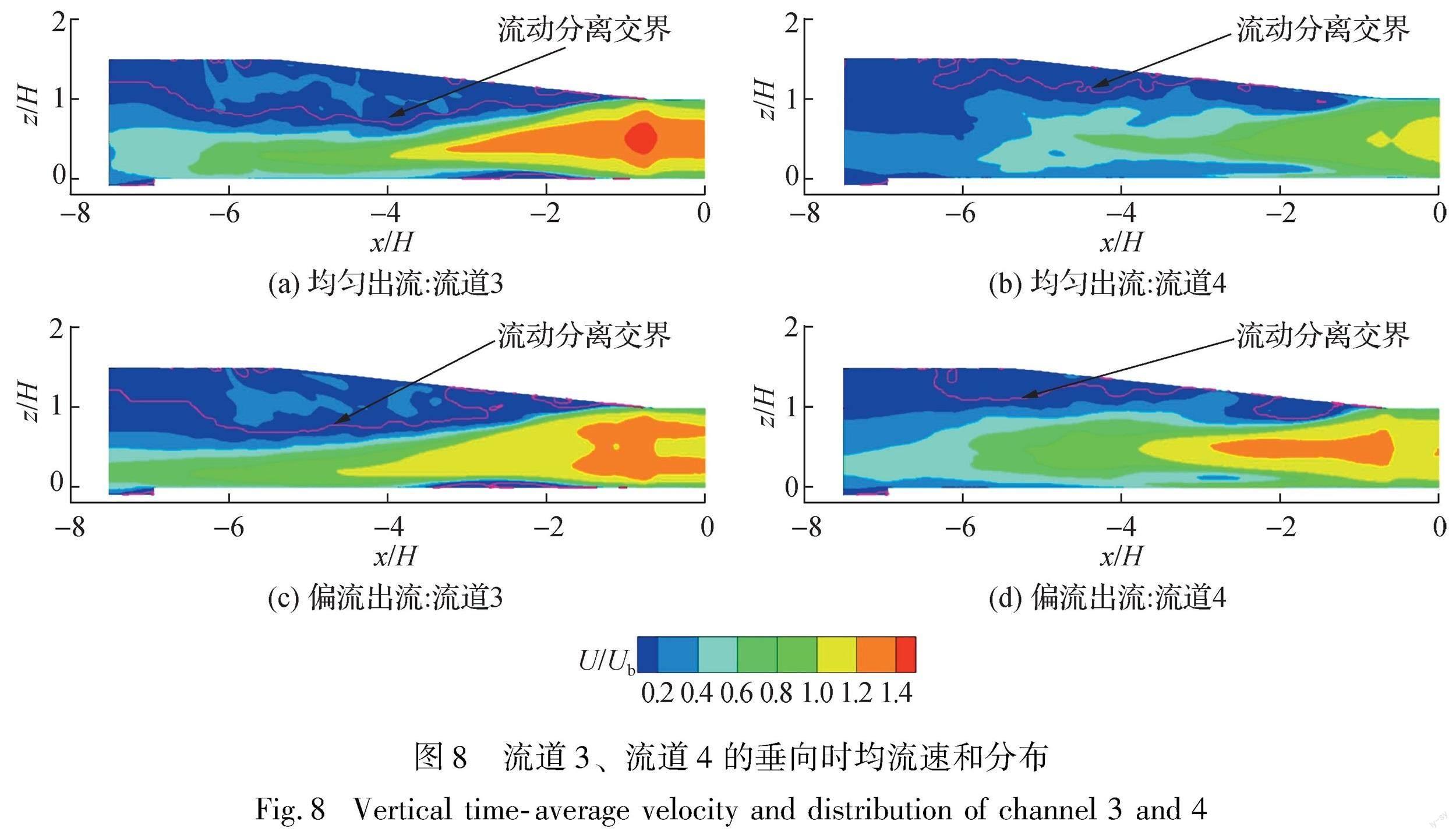
图8展示了流道3、流道4在偏流和均匀来流下的垂向时均流速分布,流道1、流道2的几何结构分别与流道3、流道4一致,计算结果接近不再重复展示。分流墩墩头处水流流速达到最大,经过垂向扩散,在x/H=-1.1发生流动分离,主流核心区靠近中下部,顶部为反向流速;沿着水流方向,主流区高度受回流的挤压而逐渐变窄。
进/出水口顶板反向流速容易造成拦污栅处流态欠佳,值得重点关注。受垂向扩散角造成流动分离的影响,扩散段顶部形成回流,通过回流系数(χ)定义,回流系数计算公式如下:
式中:u(x,z)和w(x,z)分别为x和z方向的时均流速;α为垂向扩散角。通过计算发现曲线以上的水体均为反方向流速,曲线以下的水体为正方向流速,该曲线可以视作流动分离交界。如图8所示,当水流经过垂向扩散后发生流动分离,各流道回流区的高度迅速增加,到达调整段后逐渐降低,两边流道在距离扩散段末端约1倍进口宽度的位置,即x/H=6.4,回流区高度降低为0,实现水流再附着。Tornblom等[18]通过对8.5°平面扩散器进行风洞试验,在距扩散段末端约5倍进口宽度流体重新附着,该附着现象与本文结果较为接近。两中间流道的回流面积均远大于两边流道,几乎占据扩散段面积的1/3,因此位于流道2、流道3的拦污栅更容易受到反向流速的影响。
图9为各流道断面的垂向流速分布,发现均匀来流和偏流出流下边流道1、流道4的流速分布接近且中间流道2、流道3的流速分布接近。与边流道相比,中间流道在顶部反向流速范围大,受回流区挤压造成中下部主流流速大、产生较大的逆压梯度,各流道垂向流速分布与Tornblom等试验所测流速分布相似[18,21]。如图10所示,均匀来流和偏离条件下的雷诺切应力分布相似,因此仅展示偏流出流的垂向雷诺切应力分布。在DM1处,水体质点受分流墩的影响,各流层间的动量交换较少,雷诺切应力几乎为0,此处与Tornblom等[18]试验中进口的切应力分布不同,其有压扩散器的上游为均匀槽道流衔接且紊流已充分发展,靠近两侧壁面的雷诺切应力较大而中间较小。到DM3时,流动分离显著,流层间相互混掺,在垂向上存在一正一负的峰值。DM3之后,其正向峰值逐渐降低直至为0而负向峰值逐渐减少,到扩散段末端后仅存在单个峰值,切应力分布特征与Tornblom试验结果基本一致。
2.1.3 拦污栅处流场分布
据现有文献[22-23],拦污栅处的漩滚、不利流态是造成其发生破坏的主要诱因之一。实际上,沿水流方向拦污栅刚度大,而横向的拦污栅腹板由于厚度薄更容易受到漩滚造成的疲劳破坏[6,24-25],因此拦污栅段的水流流态是重点关注的区域。如图11所示,各流道在流动分离交界处产生横轴漩涡,靠近主流区域流速和流速梯度较大,流线严重弯曲。相比边流道,中间流道的漩滚范围更大,几乎一半以上的拦污栅条处于横轴漩滚中,进一步说明中间流道容易产生疲劳破坏的风险。拦污栅横断面时均流速矢量图如图12所示,各流道在中部和底部均存在纵轴漩滚,前者由流动分离造成,后者由主流与壁面的剪切产生。为避免该区域的三轴漩滚,应严格控制垂向、横向扩散角,防止流动分离带来大面积的漩涡。
2.2 偏流出流下的紊动能和紊动强度
进/出水口水头损失关乎到水轮机的发电效益,是工程中关注的重点。前人[7]已研究各种几何因素对进/出水口水头损失的影响,计算水头损失的方法主要通过能量方程,而对进/出水口内部的水头损失分布研究较少。紊动能(K)代表脉动流速的能量,紊动能较大的区域紊流混掺剧烈,造成水流的能量损耗,反映水体质点的水头损失[6,18,26-27],其公式如下:
垂向紊动能分布如图13(a)所示,紊动能主要集中在流动分离交界,交界以上流速较小而交界以下流速较大造成能量的再分配,同时产生水头损失。从平面紊动能分布图13(b)发现,当x/H<-1.5时,紊動能主要是水平和垂直方向的流动分离造成;而当-1.5≤x/H≤-0.75时,在分流墩壁面附近发现紊动能较大的区域,造成这一现象的主要因素可能有以下2点:其一是分流墩壁面的强剪切作用,其二是分流墩附近的流动分离。
紊动强度(Tu)是影响拦污栅结构安全性的重要因素,较大的紊动强度可能会破坏拦污栅条、主次梁焊缝等结构薄弱位置[6],其公式如下:
图14为各流道不同断面的紊动强度垂向分布,紊动强度较大的区域分布在中上部和底部的流动分离交界,而位于主流核心区的紊动强度较小。DM1、DM2在主流区的紊动强度几乎为0,DM3之后主流区紊动强度缓慢增加但始终小于中上部和底部的紊动强度,该结果与Hajaali等[21]在横纵向双向扩散器的风洞试验中紊动强度垂向分布一致。因此,在拦污栅断面,流动分离交界不仅紊动强度较大,而且该区域存在三轴漩滚,流态欠佳,从而更容易造成拦污栅的破坏。
图15为对8个断面上测点的紊动强度取平均,得到8个断面的平均紊动强度。结果表明,各流道平均紊动强度沿断面分布相似,从DM1—DM8呈现出先剧增后缓慢降低的趋势,且流道1、流道2略大于流道3、流道4的紊动强度。与均匀来流相比,偏流出流下各流道在DM7(拦污栅断面)的紊动强度均较大,从流道1—流道4的紊动强度分别提高11%、25%、29%、3%。
2.3 偏流出流下的频谱分析
为了研究进/出水口的脉动动能在垂向上时间尺度的分布,对8个断面上流道中监测点的时间序列做PSD。结果如图16所示,横坐标为与底板相隔的垂直距离,纵坐标为频率。各断面的上下两侧产生能量集中的低频脉动,主频约0.02 Hz左右,与文献[28]进/出水口水流频率一致。DM1的主频位于z/H=0.9和z/H=0.1处,也是流动分离交界,远离主频区域的能量逐渐降低;到DM3时,主频幅值达到峰值,脉动动能最大,此时受顶部反向流速的影响,主频的位置发生变化,底部主频上升至z/H=0.25,顶部主频下降至z/H=0.78;DM4之后,主频位置基本不发生变化,其幅值逐渐降低。
本试验拦污栅断面水流的主频约0.02 Hz,因此由紊流作用在栅条上的力为低频脉动荷载,王光纶等[29]利用试验发现栅条固有频率为113 Hz,申永康等[30]通过对拦污栅进行模态分析得到整个栅架的一阶固有频率约14.98 Hz,均远大于紊流脉动压强的频率,因此,紊流脉动不会对拦污栅产生共振破坏。但是,鉴于主频区域的能量较大、紊动强度高,拦污栅与横梁、次梁相交的焊缝区域仍存在静疲劳破坏的风险。
3 结 论
本文利用大涡模拟方法对带水平弯段引水洞的抽水蓄能电站侧式进/出水口进行三维数值模拟,深入研究了其内部流场规律。主要结论如下:
(1) 偏流出流下,进出水口各流道水平流速分布极不均匀,主流偏向一侧,造成该侧流道的流速显著增加。在垂直方向上,主流核心区靠近过水断面中下部,扩散段垂向雷诺切应力呈一正一负峰值分布,两峰值分别源自流动分离和底部壁面剪切作用。中间流道回流区高度大于两边流道,几乎占据扩散段的1/3,因此,中间流道拦污栅更容易受到反向流速影响。
(2) 由水平、垂直扩散角引起的流动分离,是造成拦污栅处三轴漩滚的主要原因,且中间流道漩滚区域面积大于两边流道;同时在流动分离交界处的紊动强度较为集中,与均匀来流相比,偏流出流下拦污栅断面的紊动强度有明显的增加。已有工程实例表明不利的水流流态和较高的紊动强度是造成拦污栅损害的主要诱因之一,因此应重点关注处于偏流出流下流动分离交界处的拦污栅条。
(3) 进/出水口的分流墩壁面和流动分离交界处存在较大的水头损失;且其内部的流动分离造成靠近断面中上部和底部2处出现比较集中的低频脉动,主频约0.02 Hz,不会对拦污栅造成共振破坏,沿水流方向脉动的能量先增大后降低。
参考文献:
[1]孙双科,柳海涛,李振中,等.抽水蓄能电站侧式进/出水口拦污栅断面的流速分布研究[J].水利学报,2007,38(11):1329-1335.(SUN S K,LIU H T,LI Z Z,et al.Study on velocity distribution behind the trashrack in lateral intake/outlet of pumped storage power station[J].Journal of Hydraulic Engineering,2007,38(11):1329-1335.(in Chinese))
[2]王晨茜,张晨,张翰,等.侧式进/出水口流动分离现象研究[J].水力发电学报,2017,36(11):73-81.(WANG C X,ZHANG C,ZHANG H,et al.Flow separation in side inlets/outlets of pumped storage power stations[J].Journal of Hydroelectric Engineering,2017,36(11):73-81.(in Chinese))
[3]高学平,朱洪涛,刘殷竹,等.进/出水口双向流动结构流速分布与脉动规律研究[J].水利学报,2022,53(6):722-732.(GAO X P,ZHU H T,LIU Y Z,et al.Research on velocity distribution and fluctuation law of bidirectional flow structure of inlet/outlet[J].Journal of Hydraulic Engineering,2022,53(6):722-732.(in Chinese))
[4]朱洪涛,高学平,刘殷竹.进/出水口出流扩散脉动流速规律试验研究[J].水力发电学报,2022,41(7):129-139.(ZHU H T,GAO X P,LIU Y Z.Experimental study of velocity fluctuations in inlet/outlet under outflow diffusion[J].Journal of Hydroelectric Engineering,2022,41(7):129-139.(in Chinese))
[5]YE F,GAO X P.Numerical simulations of the hydraulic characteristics of side inlet/outlets[J].Journal of Hydrodynamics:Ser B,2011,23(1):48-54.
[6]高学平,刘永朋,孙博闻,等.侧式进/出水口扩散出流紊动强度变化规律研究[J].水利水电技术,2020,51(3):91-100.(GAO X P,LIU Y P,SUN B W,et al.Study on variation law of turbulence intensity of diffused outflow at lateral inlet/outlet[J].Water Resources and Hydropower Engineering,2020,51(3):91-100.(in Chinese))
[7]徐准,吴时强.抽水蓄能电站侧式进/出水口隔墩布置对水力特性的影响[J].水利水电科技进展,2020,40(3):21-27,67.(XU Z,WU S Q.Influence of arrangement of division piers in lateral inlet and outlet of pumped storage plants on hydraulic characteristics[J].Advances in Science and Technology of Water Resources,2020,40(3):21-27,67.(in Chinese))
[8]张兰丁.响水涧抽水蓄能电站上、下库进(出)水口分流特性研究[J].水利水电科技进展,2010,30(6):48-52.(ZHANG L D.Flow-dividing characteristics of intakes/outlets in upper and lower reservoirs of Xiangshuijian pumped storage station[J].Advances in Science and Technology of Water Resources,2010,30(6):48-52.(in Chinese))
[9]張从联,朱红华,钟伟强,等.惠州抽水蓄能电站下库进出水口水工模型试验研究[J].人民珠江,2003,24(6):10-14.(ZHANG C L,ZHU H H,ZHONG W Q,et al.Hydraulic modelling of inlet/outlet of lower reservoir for Huizhou pump storage plant[J].Pearl River,2003,24(6):10-14.(in Chinese))
[10]丁全林,汪德爟,王玲玲.基于LBGK方法的粘性流体晃动问题大涡模拟[J].水科学进展,2009,20(5):652-657.(DING Q L,WANG D G,WANG L L.LES of viscous liquid sloshing problem based on the LBGK method[J].Advances in Water Science,2009,20(5):652-657.(in Chinese))
[11]王文全,张立翔,郭亚昆,等.弯曲槽道边壁振动情况下湍流特性的大涡模拟[J].水科学进展,2008,19(5):618-623.(WANG W Q,ZHANG L X,GUO Y K,et al.LES of turbulent flow in a vibrating curved-wall channel[J].Advances in Water Science,2008,19(5):618-623.(in Chinese))
[12]徐振山,陈永平,张长宽.波流环境中垂向圆管射流三维运动和稀释过程模拟[J].水科学进展,2017,28(2):265-275.(XU Z S,CHEN Y P,ZHANG C K.Study on three-dimensional movement and dilution of a vertical round jet under the wave-current effect[J].Advances in Water Science,2017,28(2):265-275.(in Chinese))
[13]SMAGORINSKY J.General circulation experiments with the primitive equations:I:the basic experiment[J].Monthly Weather Review,1963,91(3):99-164.
[14]徐振山,陈永平,张长宽,等.波流环境中射流的大涡数值模拟[J].水科学进展,2014,25(2):239-245.(XU Z S,CHEN Y P,ZHANG C K,et al.Large eddy simulation of a jet in wave-current environment[J].Advances in Water Science,2014,25(2):239-245.(in Chinese))
[15]LILLY D K.A proposed modification of the Germano subgrid‐scale closure method[J].Physics of Fluids A:Fluid Dynamics,1992,4(3):633-635.
[16]HERBST A H,SCHLATTER P,HENNINGSON D S.Simulations of turbulent flow in a plane asymmetric diffuser[J].Flow,Turbulence and Combustion,2007,79(3):275-306.
[17]OBI S,NIKAIDO H,MASUDA S.Reynolds number effect on the turbulent separating flow in an asymmetric plane diffuser[C]∥Proceedings of the ASME/JSMR Fluids Engineering Division Summer Meeting.New York:American Society of Mechanical Engineers,1999.
[18]TRNBLOM O,LINDGREN B,JOHANSSON A V.The separating flow in a plane asymmetric diffuser with 8.5° opening angle:mean flow and turbulence statistics,temporal behaviour and flow structures[J].Journal of Fluid Mechanics,2009,636:337-370.
[19]張兆顺,崔桂香,许春晓.湍流理论与模拟[M].北京:清华大学出版社,2005.(ZHANG Z S,CUI G X,XU C X.Theory and modeling of turbulence[M].Beijing:Tsinghua University Press,2005.(in Chinese))
[20]王文娥,廖伟,漆力健.宽窄相间河道水流紊动特性试验研究[J].水科学进展,2020,31(3):394-403.(WANG W E,LIAO W,QI L J.Experiment of turbulent characteristics of flow in wide-and-narrow channels[J].Advances in Water Science,2020,31(3):394-403.(in Chinese))
[21]HAJAALI A,STOESSER T.Flow separation dynamics in three-dimensional asymmetric diffusers[J].Flow,Turbulence and Combustion,2022,108(4):973-999.
[22]皮仙槎.抽水蓄能电站拦污栅的设计[J].水力发电学报,1990,9(4):86-93.(PI X C.Design of trash rack in pumped storage power station[J].Journal of Hydroelectric Engineering,1990,9(4):86-93.(in Chinese))
[23]XUE B,MAO Y P,ZHANG C H,et al.Nonlinear fluid-induced vibro-impact analysis on the fatigue failure pattern of a large-scale trashrack with a reduced-order model[J].Structures,2023,49:467-478.
[24]潘钦.抽水蓄能电站拦污栅流激振动研究[D].大连:大连理工大学,2007.(PAN Q.Study on flow-induced vibration of trash racks of pumped-storage hydroelectric plants[D].Dalian:Dalian University of Technology,2007.(in Chinese))
[25]钟耀.基于试验的拦污栅的激振分析及体型优化研究[D].大连:大连理工大学,2008.(ZHONG Y.Research on flow-induced vibration and body type optimization of trashracks based on test[D].Dalian:Dalian University of Technology,2008.(in Chinese))
[26]陳启刚,钟强.明渠紊流中涡结构的运动规律[J].水科学进展,2017,28(4):579-587.(CHEN Q G,ZHONG Q.Experimental study on the movement of vortices in turbulent open-channel flows[J].Advances in Water Science,2017,28(4):579-587.(in Chinese))
[27]廖伟,张维乐,王文娥,等.臂坡对堰槽组合设施紊流结构影响试验研究[J].水科学进展,2023,34(3):465-479.(LIAO W,ZHANG W L,WANG W E,et al.Experimental study on the effect of arm slope on turbulent structure of weir-flume combination[J].Advances in Water Science,2023,34(3):465-479.(in Chinese))
[28]高学平,袁野,刘殷竹,等.拦污栅结构对进出水口水力特性影响试验研究[J].水力发电学报,2023,42(2):74-86.(GAO X P,YUAN Y,LIU Y Z,et al.Experimental study on effect of trash rack structure on hydraulic characteristics of inlet and outlet[J].Journal of Hydroelectric Engineering,2023,42(2):74-86.(in Chinese))
[29]王光纶,张文翠,李未显.抽水蓄能电站拦污栅结构振动特性模型试验研究[J].清华大学学报(自然科学版),2001,41(2):114-118.(WANG G L,ZHANG W C,LI W X.Experimental study of the free vibration characteristics of the trashrack of the Tianhuangping pumped storage station[J].Journal of Tsinghua University (Science and Technology),2001,41(2):114-118.(in Chinese))
[30]申永康,方寒梅,赵春龙,等.大型拦污栅结构液固耦合流激振动分析[J].振动与冲击,2014,33(21):137-141.(SHEN Y K,FANG H M,ZHAO C L,et al.Flow-induced vibration of large trash-racks considering fluid-structure interaction[J].Journal of Vibration and Shock,2014,33(21):137-141.(in Chinese))
Study on large eddy simulation of lateral inlet/outlet under bending outflow
Abstract:Due to the influence of topography and geology in actual engineering projects,water tunnels often have horizontal bends.These bends result in non-uniform inflow conditions,complicating the turbulence characteristics at the inlet and outlet compared to straight-line tunnels.This study employs Large Eddy Simulation to analyze a real engineering problem.The calculated results are compared with experimental data,revealing close agreement in flow velocity and probability density distribution.The findings show that under outflow conditions,the flow-split ratios for each channel are 0.64,0.81,1.26,and 1.29,indicating a highly non-uniform horizontal velocity distribution.In the vertical direction,the main flow occurred primarily in the lower middle section,and the vertical Reynolds shear stress in the diffusion segment exhibits a distinctive pattern with alternating positive and negative peaks.This phenomenon is primarily attributed to flow separation in the upper middle area and wall shearing near the bottom.The recirculation region′s height in the two middle channels was found to be greater than that in the side channels,indicating that trash racks in the central channels are more susceptible to reverse flow velocities.Additionally,flow separation near the trash rack gives rise to a three-axis vortex,while two energy-concentrated pulsations occur in the upper middle section and near the bottom.Moreover,under bending flow conditions,turbulence intensities in different channels increase by 11%,25%,29%,and 3%,respectively,compared to those in uniform flow situations.Consequently,the unfavorable flow regime and high turbulence intensity associated with bending flow pose a threat to the trash rack.
Key words:lateral inlet/outlet;bending flow;Reynolds shear stress;flow separation;low frequency pulsation

