复杂载荷下的核管路支架智能布置
孙宇翔 陈丽 龙波 王艳苹 刘诗华 贾坤

摘要 :当前,核电管路支架布置通过人工试算反复迭代来实现,存在劳动强度大、设计周期长、成本高等缺点。借助管路有限元力学分析,提出一种基于粒子群 遗传混合算法的三维空间核电管路支架智能布置方法。布置示例表明,所提方法可在管路的三维全局空间内自动布置不同功能的多个支架,在满足《压水堆核岛机械设备设计和建造规则》设计规范的同时减小了工作量。
关键词 :核电管路;支架布置;智能布置;粒子群 遗传混合算法
中图分类号 :TM623.2
DOI:10.3969/j.issn.1004-132X.2024.02.016
开放科学(资源服务)标识码(OSID):
Intelligent Layout for Pipeline Supports of Nuclear Power Plant under
Complex Load
SUN Yuxiang 1 CHEN Li 2 LONG Bo 2 WANG Yanping 2 LIU Shihua 2 JIA Kun 1
1.State Key Laboratory for Strength and Vibration of Mechanical Structures,Xian Jiaotong
University,Xian,710049
2.Center of Mechanics,China Nuclear Power Engineering Co.,Ltd.,Beijing,100840
Abstract : Nowadays, the arrangement of pipeline supports for nuclear power plants is achieved by iterative manual calculations, which had many drawbacks such as high labour intensity, long design cycles, and high costs. An intelligent layout method for three-dimensional nuclear power pipeline supports was proposed based on particle swarm optimization-genetic algorithm hybrid algorithm and finite element mechanics analysis. The examples of intelligent arrangement of pipeline supports for typical nuclear pipelines show that the proposed method may automatically arrange multiple supports of different types in the global space of the pipeline to meet the Design and Construction Rules for Mechanical Equipment of Nuclear Island of Nuclear Power Plants, and greatly reduce workload.
Key words : nuclear power pipeline; pipeline support arrangement; intelligent layout; particle swarm optimization-genetic algorithm hybrid algorithm
0 引言
支架作为固定、支撑及准确定位核电管路的重要设施,是确保管路及其连接设备运行安全稳定的重要屏障。支架布置需保证管路在温度、地震、自重等复杂条件下满足力学性能要求 [1-3] 。随着“华龙一号”商业运营的不断推广,以往的参考设计难以满足核电自主设计的需求。人工反复调整支架位置和功能的布置策略存在劳动强度大、设计周期长、成本高的缺点,且性能难以达到最优。因此,借助人工智能领域的最新成果来发展核电管路支架的自动布置方法是提高设计效率和经济性的有效途径,并对提高核电自主设计能力和技术创新具有重要作用。
近年来,国内外学者在非核级管路支架的智能布局优化方面取得了一定成果。为减少流动和振动载荷产生的过高应力导致的管路故障、破坏及寿命损失,粒子群算法、遗传算法、灰狼算法等智能方法 [4-5] 被用于管路支架的优化,以实现对管路基频、振动响应等目标的控制。采用伪密度变量技术可将支架布局问题转化为以固有频率最大为目标的连续体拓扑优化问题 [6-9] 。LIU等 [10] 针对航空发动机管路布局与支架排布的耦合问题, 提出一种管路布局和支架排布的集成优化方法,引入Levy飞行策略对MOALO(multiobjective ant lion optimizer)算法进行改进,在保证管路和支架之间装配约束的前提下, 实现了管路支架系统的总体布局优化。GAO等 [11] 为减小振动对管路系统的影响,通过神经网络建立优化输入与输出关系的代理模型,利用遗传算法对支架位置进行优化。
核级管路设计需考虑高温、高压、自重、冲击和地震等极端工况,因此非核级管路支架智能布置的研究成果难以直接应用。已有研究多着眼于核级管路的自动化排布 [12-13] ,仅有少数学者考虑力学性能对核管路支架位置进行优化。姜圣翰等 [14] 先对管路进行预处理,再使用支持向量机进行合格节点分类,最后使用穷举法、云计算找出支架的最优排布。该方法充分利用了云计算的计算效能,但不具备智能化设计特征,且前处理阶段较为复杂、智能化程度较低、专业知识门槛较高,通用性不足。白晓明等 [15] 在总结人工试算方法的基础上,开发了基于遗传算法的核级管路优化布置方法,即将管路上支架的局部位置和功能作为优化变量,以多种工况下管路的最大应力与许用应力之比作为优化目标,使用遗传算法寻找支架的优化布置方案。该方法对支架可布置范围进行了限定,單个支架只能在某段管路上移动,无法实现三维管路的全局寻优。此外,该方法仅约束了管道的最大应力与许用应力之比,未考虑《压水堆核岛机械设备设计和建造规则》对阀门加速度的要求,无法直接用于复杂载荷下三维空间管路支架位置的工程设计。
為满足工程设计需求,本文提出一种复杂载荷下三维空间核管路支架的智能布置方法,以管路的有限元力学分析为基础,利用粒子群 遗传(particle swarm optimization-genetic algorithm, PSO-GA)混合算法在整条管路对应的空间坐标中选择每个支架的最优位置,解决遗传算法收敛慢的问题。该方法依据《压水堆核岛机械设备设计和建造规则》(RCC-M),以设计工况、正常工况、异常工况、事故工况下的管路最大应力与许用应力之比总和最小为优化目标,同时施加力学约束条件(4种工况下的最大应力与许用应力之比均小于1,地震荷载SL-1、SL-2作用下的阀门加速度分别小于4.8 g 和6.0 g ),通过PSO-GA混合算法自动迭代获取最优的管路支架布置方案。
1 核级管路支架布置的要求
1.1 支架布置规则
管路支架根据约束自由度的多少可分为滑动支架、导向支架、固定支架;根据反作用力形式可分为弹簧支架、刚性支架、恒力支架。滑动支架仅约束管路的径向位移,而允许管路沿轴向移动,主要用于限制管路重力方向移动产生的脱节。导向支架牵引管路沿特定方向移动,避免偏离指定方向。限位支架限制管路从某个方向或几个方向的线位移或角位移。弹簧支架允许管路自由移动,并能有效承载管路负荷、应对热膨胀。刚性支架将荷载传递到主体结构。 恒力支架是管路产生热位移较大时采用的一种支架。
支架位置、形式和数量的选取直接影响管路的应力分布。支架位置选取的传统方法主要根据设计准则及经验控制支架间距,避免管路因复杂荷载产生过大的应力,水平方向的管路支架设置尤其要避免弯曲产生过大的正应力、剪应力和挠度。从工程角度出发,在满足设计要求的前提下,应采用安装简单、成本较低的支架,并尽量减少支架的种类和数目。
1.2 复杂载荷下的应力准则
核管路的安全性评价一般通过管路的应力分析与计算来实现。核管路的支架首先应能承受管路及在线设备的静荷载(包括压力、自重和热膨胀载荷),保证管路自身应力小于许用值。某型核管路系统工作时,管路内流体的温度超过300℃ [16] ,因此支吊架布置需考虑管路的热胀冷缩问题,以免管路膨胀后的热应力导致管路应力超出材料的许用极限。其次,还需考虑动荷载和偶然荷载的作用,保证管路在地震作用下的应力不超过许用极限,仍能够正常发挥作用。
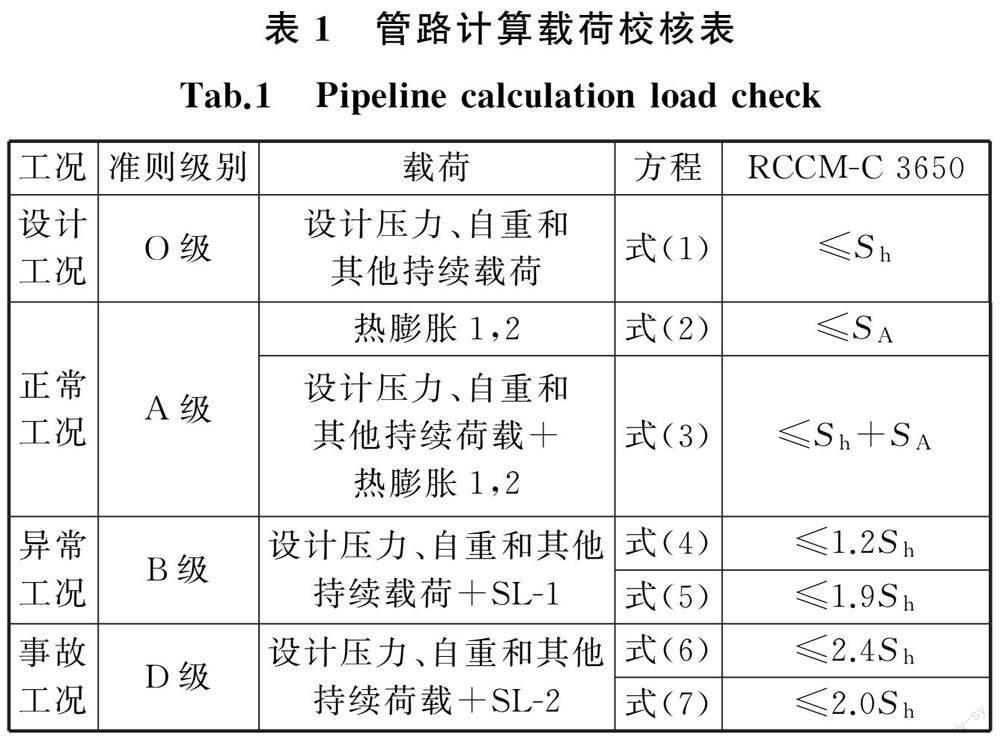
合格的管路支架布置应使整个管路系统的应力满足相应规范的要求,通常要保证核管路在设计工况(压力、自重和持续载荷),正常工况(压力、自重、持续载荷和热膨胀),异常工况(压力、自重、持续载荷和运行基准地震载荷),以及事故工况(压力、自重、持续载荷和安全停堆地震载荷)下都满足相应的评定准则。因此,本文采用RCC-M设计规范中不同工况下的核管路许用应力及计算方法 [17] 。表1中,正常工况下,热膨胀1的载荷为温度80 ℃、压力0.2 MPa,热膨胀2的载荷为温度40 ℃、压力0.2 MPa;异常和事故工况下运行基准地震载荷SL-1、安全停堆地震载荷SL-2的地震谱分别如图1所示。SL-1、SL-2地震谱引起的荷载施加在管路1.25 m高位置,阻尼比设置 为3%。
(1)O级准则要求:管道中应力满足
S SL = pD o 4t n +0.75i M A Z ≤S h (1)
式中,S SL 为 O 级准则应力计算值;p为设计压力;D o 为管道外径;t n 为公称壁厚;M A 为由重量和其他持续荷载引起的合力矩;Z为管道载面模量;i为应力增强系数;S h 为设计温度下材料的基本许用应力。
(2) A 级准则要求:热膨胀应力超过 RCCM-C 3650 给定的许用变化范围S A 时,若不满足
S E = iM c Z ≤S A (2)
式中,M c 为热膨胀产生力矩的变化范围;S E 为 A 级准则的热膨胀应力计算值。
的要求,则可用下式
S TE = pD o 4t n + i Z (0.75M A +M c )≤S h +S A (3)
式中,S TE 为 A 级准则中考虑持续载荷和热载荷的应力计算值。
继续校核,若式(3)得到满足,则此工况热膨胀应力符合 RCC-M 设计规范要求。
(3) B 级准则要求:
S a,B = p max D o 4t n + 0.75i Z (M A +M B )≤1.2S h (4)
式中,p max 为考虑工况下的最大压力;M B 为偶然载荷产生的合力矩;S a,B 为 B 级准则中考虑持续载荷和偶然载荷的应力计算值。
(4) D 级准则要求:
S a,D = p max D o 4t n + 0.75i Z (M A +M B )≤2.4S h (5)
如果 p max D 0 2t n ≤S h ,则只需管路应力满足如下条件:
S′ a,D = 0.75i Z (M A +M B )≤1.9S h (6)
此外,在仅考虑内部压力时,管路应力应满足如下条件:
S″ a,D = p max D o 2t n ≤2S h (7)
式中,S a,D 为 D 级准则中考虑持续载荷和偶然载荷的应力计算值;S′ a,D 为 D 级准则中不考虑内压、仅考虑其他持续载荷和偶然载荷下计算所得应力;S″ a,D 为 D 级准则中仅考虑内压时计算所得的应力。
除此之外,特殊管路还需要考虑管路阀门的加速度、接口复杂载荷等情况。
2 基于 PSO-GA 混合算法的支架智能 布置
在载荷环境、管路布置及支架种类数目确定的情况下,支架位置是决定管路应力的唯一因素。管路构型复杂,无法建立最大应力的解析表达式,也难以得到支架位置与管路应力间关系的代理模型。为此,本文以有限元管路应力分析为基础,通过PSO-GA混合算法对随机生成的初始支架位置进行优化。PSO-GA混合算法将遗传算法的种群多样性、全局随机搜索能力与粒子群算法的个体记忆、收敛快等特性相结合,可有效提高迭代速率,增强寻优能力,从而克服遗传算法收敛慢的缺点。对于管路支架優化,PSO-GA混合算法通过粒子群算法生成当代最优个体(当代最优的支架布置信息),并使用遗传算法对个体种群(支架布置信息集)进行交叉、变异、精英种群选取,反复迭代得到最优解(最优的支架布置信息),并保证管路最大应力与许用应力之比、阀门加速度满足RCC-M准则。
优化目标设计为管路系统4种工况下的最大应力与许用应力之比的总和最小。设置约束条件:地震荷载SL-1、SL-2作用下的阀门加速度分别小于4.8 g 和6.0 g ;4种工况的最大应力与许用应力之比均小于1。优化数学模型为
min ( S SL S h + max ( S E S A , S TE S h +S A )+ S a,B S h +
max ( S a,D 2.4S h , S′ a,D 1.9S h , S″ a,D 2S h ))
s.t. S SL S h ≤1
max ( S E S A , S TE S h +S A )≤1
S a,B S h ≤1
max ( S a,D 2.4S h , S′ a,D 1.9S h , S″ a,D
2S h )≤1 (8)
基于 PSO-GA 混合算法的支架位置智能布置流程如图2所示。以支架位置、种类为优化变量,首先生成包含支架位置信息的粒子种群,使用 PIPESTRESS 软件并基于梁单元对初始粒子种群个体构建力学模型。根据约束条件、优化目标,计算粒子个体的适应度、极值,以及种群极值。根据个体极值与种群极值对粒子种群的速度、位置进行更新,随后对更新后粒子的个体适应度、个体极值、种群极值进行更新。 最后判断是否满足终止条件,若不满足则将该种群作为父代种群进行交叉、变异,得到子代种群,父代与子代种群合并通过精英种群策略筛选,最终得到关于支架位置信息的下一代粒子种群。反复迭代,直至某一支架位置布置的管路力学模型计算结果符合力学评定准则或达到终止迭代次数,输出当前支架的位置信息。
3 智能布置算例
针对图3所示的核电站一回路典型管路,以本文方法对管路支架进行智能布置。为展现 PSO-GA混合算法的优势,对比分析了本文算法和非支配排序遗传算法(NSGA) [15] 的布置效果。取A点为笛卡儿坐标系原点,管路中任意节点位置可用空间坐标(x,y,z)表示。管路外径 273.1 mm,壁厚9.27 mm,线密度60.31 kg/m,抗震等级为1F。阀门长度为600 mm,重心位于(400 mm,0,0),质量为250 kg,抗震等级为1A。考虑的工况包括设计工况、正常工况、异常工况、事故工况。本文的智能布置方法不仅能保证管路在上述4种工况下满足力学约束条件,还可使管路在上述4种工况下的最大应力与许用应力之比总和最小。
3.1 支架布置预处理
使用PIPESTRESS有限元软件构建管路模型,其中,TANG单元模拟直管,BRAD单元模拟弯管,VALV单元模拟阀门。考虑到管路总长36.98 m,为平衡计算效率与优化效果,采取等间距0.1 m划分节点,并对节点位置进行编号,以确定节点位置信息,管路节点编号见图4。阀门仅考虑集中质量并加载于管路节点上,管路支架布置在管路的节点位置。
阀门、三通管、弯管附近不布置支架。作为实例,共选用5个支架,其中,2个为只约束管路平动侧向和竖向的 GL 支架,2个为约束Z向平动的 BV 支架,1个为固定约束的 CB 支架,支架刚度100 MN/m。
3.2 支架智能布置过程
3.2.1 初始粒子种群的产生
设置管路支架最大可调控的空间位置信息为控制变量的上限X ub ,最小可调控的空间位置信息为控制变量的下限X lb ,在上限与下限之间取任意的整数作为支架的落点位置X,则有X lb ≤X≤X ub 。设定种群的个体数量为50,随机生成包含多个随机初始支架位置信息的初始粒子种群。根据初始支架位置信息建立 PIPESTRESS 软件的力学模型。
3.2.2 个体适应度的产生
每种支架位置信息对应4种工况下的最大应力与许用应力之比的总和。以最大应力与许用应力之比的总和的倒数作为 PSO-GA 混合算法中个体的适应度F:
F=[ S SL S h + max ( S E S A , S TE S h +S A )+ S a,B S h + max ( S a,D 2.4S h , S′ a,D 1.9S h , S″ a,D 2S h )] -1 (9)
若個体不满足约束条件,则适应度为0。
3.2.3 粒子种群位置与速度的更新
设置算法中最优解(极值)为4种工况下最大应力与许用应力之比的总和最小,最大迭代次数G max 为20。为达到所有粒子向最优解靠拢的目的,位置、速度迭代公式为
v id =wv id +c 1r 1(P id -X id ) + c 2r 2(P ig -X id ) (10)
X i+1 =X i+v i+1
c 1=c 1s +(c 1e -c 1s )G max /i
c 2=c 2s +(c 2e -c 2s )G max /i
式中,v id 为第i次迭代第d个粒子的速度;w为惯性因子;c 1、c 2分别为个体学习因子和全局学习因子;r 1、r 2为0~1的随机数;P id 为第i次迭代后第d个粒子个体的最优解位置;P ig 为第i次迭代后,全局最优解的粒子位置;X i+1 、X i 分别为第i+1次迭代和第i次迭代的粒子位置;c 1 s 、c 1 e 分别为初始个体学习因子和最终个体学习因子,c 1 s = 2.75, c 1 e =1.25;c 2 s 、c 2 e 分别为初始社会学习因子和最终社会学习因子,c 2 s =0.50, c 2 e =2.25。
本文使用非对称学习因子 [18] ,以使 PSO-GA 混合算法迭代前期的全局搜索能力强,迭代后期的局部搜索能力变强,惯性因子线性迭代公式为
w=w s -(w s -w e )(i/G max ) 2 (11)
式中,w s 、w e 分别为初始权重和最终权重,w s =0.9, w e =0.4。
3.2.4 迭代寻优
比较不同粒子个体的适应度,将适应度较高的个体作为精英粒子种群个体保留遗传到下一代。粒子位置都是整数,因此将粒子种群个体信息进行二进制编码(图5),通过交叉变异生成新的粒子种群个体,解码后根据位置速度迭代公式更新粒子位置与速度,重复上述步骤直至满足终止条件,输出当前结果。此外,考虑到算法中参数的设定值会直接影响算法的高效性与稳定性,本文通过对交叉参数、变异算子进行敏感性分析,发现交叉参数对优化目标影响最敏感。为此,重点调试交叉参数值,观察不同参数值对优化效果的影响,最终选择优化效果最佳的参数值:随机片段交叉参数为0.7,随机点位变异参数为0.3。
3.3 智能布置结果
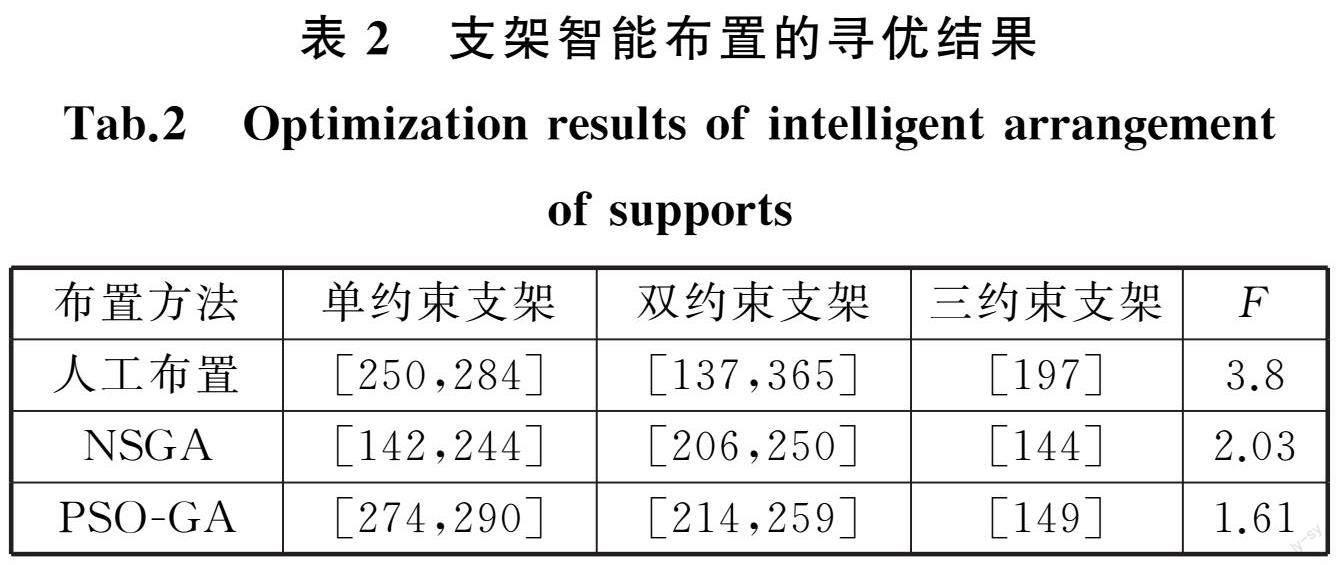
表2给出了人工布置、NSGA算法迭代20次、PSO-GA混合算法迭代20次后,4种工况下最大应力与许用应力之比的总和 F 最优的支架 位置。图6~图8分别为人工布置、NSGA算法迭代20次、PSO-GA混合算法迭代20次后的应力比云图。由图6可以看出,人工支架布置不满足RCC-M设计规范,NSGA算法和PSO-GA混合算法皆能满足RCC-M规范。
NSGA算法与PSO-GA混合算法不同迭代次数的最大应力与许用应力之比的总和见图9。PSO-GA混合算法克服了NSGA算法前期收敛较慢的缺点,具有更好的寻优效果。如图10所示,相较于手动调试、NSGA算法,PSO-GA混合算法的优化效果更为显著,更好满足设计要求。正常工况下,PSO-GA混合算法的最大应力与许用应力之比仅为0.2,远低于RCC-M设计规范的许用值。
PSO-GA混合算法迭代20次后, 管路中2個阀门在地震荷载SL-1下的合加速度分别为1.32 g 和2.02 g ,在地震荷载SL-2下的合加速度分别为1.92 g 和 2.91 g ,满足阀门加速度的约束条件。综合考虑计算效率和优化效果,将PSO-GA混合算法迭代20次的管路支架位置作为最优支架布置方案,如图11所示,其中,单约束支架位于274节点、290节点,双约束支架位于214节点、259节点,三约束支架位于149节点。
4 结论
本文提出了一种基于PSO-GA混合算法的核电管路支架智能布置方法。算例表明该方法适用于复杂载荷下三维核管路的支架智能布置,能在管路对应的全局空间内通过支架位置迭代找到功能支架的最优位置。所得支架布置下,管路4种工况的最大应力与许用应力之比的总和为 1.61。 同时,4种工况下最大应力与许用应力之比均小于1,地震荷载SL-1下管路中两个阀门的合加速度分别为1.32 g 和2.02 g ,地震荷载SL-2下管路中两个阀门的合加速度分别为1.92 g 和 2.91 g ,远低于RCC-M规范中的许用值。本文提出的方法充分考虑了核电管路工程设计的实际要求,相比于传统的手动调试,本文方法在满足设计需求的同时极大减少了工作量。
参考文献 :
[1] 王新军,卢喜丰,艾红雷,等.核级高能管道系统优化分析[J].核动力工程,2014,35(4):114-118.
WANG Xinjun, LU Xifeng, AI Honglei, et al. Optimization Analysis of Nuclear Grade High Energy Pipeline System[J]. Nuclear Power Engineering, 2014,35(4):114-118.
[2] 陈敏,张周红.复杂管道应力分析中的支吊架布置方法[J].压力容器,2009,26(3):21-25.
CHEN Min, ZHANG Zhouhong. Arrangement Method of Support and Hanger in Stress Analysis of Complex Pipeline[J]. Pressure Vessel, 2009, 26(3):21-25.
[3] 白晓明,郑连纲,王新军,等.基于遗传算法的核级管道力学性能优化研究[J].核动力工程,2017,38(S2):46-49.
BAI Xiaoming, ZHENG Liangang, WANG Xinjun,et al. Research on Mechanical Performance Optimization of Nuclear-level Pipeline Based on Genetic Algorithm[J]. Nuclear Power Engineering, 2017, 38(S2):46-49.
[4] MENDOZA F, BERNAL-AGUSTIN J L, DOMINGUEZ-NAVARRO J A. NSGA and SPEA Applied to Multi-objective Design of Power Distribution Systems[J]. IEEE Transactions on Power Systems, 2006, 21:1938-1945.
[5] GOLDBERG D E. Genetic Algorithm in Search, Optimization, and Machine Learning[M]. Hoboken:Addison Wesley Pub. Co., 1989.
[6] 徐培原,刘伟.发动机外部管路系统的卡箍布局多目标优化[J].航空发动机,2020,46(6):46-52.
XU Peiyuan, LIU Wei. Multi-objective Optimization of Clamp Layout of Engine External Piping System[J]. Aero Engine, 2020, 46(6):46-52.
[7] 柳强, 焦国帅. 基于Kriging模型和NSGA-Ⅱ的航空发动机管路卡箍布局优化[J]. 智能系统学报, 2019, 14(2):281-287.
LIU Qiang, JIAO Guoshuai. Layout Optimization of Aero-engine Piping Clamps Based on Kriging Model and NSGA-Ⅱ[J]. Journal of Intelligent Systems, 2019, 14(2):281-287.
[8] 刘旭东, 孙伟. 多卡箍支撑的管路系统振动特性半析建模及支撑位置优化[J]. 振动与冲击, 2021, 40(9):32-40.
LIU Xudong, SUN Wei. Semi-analytical Modeling of Vibration Characteristics of Pipeline System Supported by Multiple Clamps and Optimization of Support Position[J]. Vibration and Shock, 2021, 40(19):32-40.
[9] 赵红飞,柳强. 考虑装配约束的航空发动机卡箍布局GWO优化[J]. 辽宁石油化工大学学报, 2022, 42(1):92-96.
ZHAO Hongfei, LIU Qiang. GWO Optimization of Aero-engine Clamp Layout Considering Assembly Constraints[J]. Journal of Liaoning Petrochemical University, 2022, 42(1):92-96.
[10] LIU Qiang, TANG Zhi, LIU Huijuan, et al. Integrated Optimization of Pipe Routing and Clamp Layout for Aeroengine Using Improved MOALO[J]. International Journal of Aerospace Engineering, 2021, 2021:6681322.
[11] GAO Peixin, LI Jinwu, ZHAI Jingyu, et al. A Novel Optimization Layout Method for Clamps in a Pipeline System[J]. Applied Sciences, 2020, 10(1):1-16.
[12] GONG Xiaocheng, JIN Xianjing, ZHANG Yu. Research and Application of Automatic Modeling Technology for Mechanical Analysis of Nuclear Power Pipelines Based on PepS[C]∥Proceedings of the 29th International Conference on Nuclear Engineering. Beijing, 2022:V012T12A013.
[13] ZHANG Jie, WU Liangjun, HU Jiakun, et al. Research and Application of Intelligent Layout Design Algorithm for 3D Pipeline of Nuclear Power Plant[J]. Mathematical Problems in Engineering, 2022, 2022:5198724.
[14] 姜圣翰,范凯,王用超,等.云计算在核级管道应力分析与优化设计中的应用研究[J].核動力工程, 2021, 42(S2):150-153.
JIANG Shenghan, FAN Kai, WANG Yongchao, et al. Application of Cloud Computing in Stress Analysis and Optimal Design of Nuclear Grade Pipelines[J]. Nuclear Power Engineering, 2021,42 (S2):150-153.
[15] 白晓明,王新军,张锐,等.智能优化算法在华龙一号核级管道布置优化中的应用[J].核动力工程, 2019, 40(S1):41-44.
BAI Xiaoming, WANG Xinjun, ZHANG Rui, et al. Application of Intelligent Optimization Algorithm in Layout Optimization of Hua Long No.1 Nuclear Pipeline[J]. Nuclear Power Engineering, 2019, 40(S1):41-44.
[16] 蒲小芬,王俭.秦山核电二期工程主管道的设计和安装[J].核动力工程,2003(S1):185-187.
PU Xiaofen, WANG Jian. Design and Installation of the Main Pipeline of Qinshan Nuclear Power PhaseII Project[J]. Nuclear Power Engineering, 2003(S1) :185-187.
[17] AFCEN. Design and Construction Rules for Mechanical Components of PWR Nuclear Islands, RCC-M Section I:Subsection C-2002[S]. Shanghai:Shanghai Scientific and Technological Literature Press, 2010:149-151.
[18] 毛开富,包广清,徐驰.基于非对称学习因子调节的粒子群优化算法[J].计算机工程,2010,36(19):182-184.
MAO Kaifu, BAO Guangqing, XU Chi. Particle Swarm Optimization Algorithm Based on Asymmetric Learning Factor Adjustment[J]. Computer Engineering, 2010,36 (19):182-184.
( 编辑 张 洋 )
作者简介 :
孙宇翔 ,男,2000年生,博士研究生。研究方向为管路智能优化。E-mail:yuxiangsun@stu.xjtu.edu.cn。
贾 坤 (通信作者),男,1986年生,副教授、博士研究生导师。研究方向为核工程力学。发表论文30余篇。E-mail:kunjia@mail.xjtu.edu.cn.

