基于孪生人工蜂鸟算法的多作业模式半导体封测环节调度
王洪 吴立辉 陈达 张洁
摘要 :针对多作业模式的半导体封装测试环节调度问题,以最小化最大完工时间为目标,提出了孪生人工蜂鸟算法。设计了孪生种群机制,通过构建双解码、孪生种群生成与协作方法,扩大解的搜索空间,提高初始解的质量,增加优化过程中解的多样性,进而提高求解精度。通过双向引导觅食策略,平衡算法多样性与收敛性,增强算法稳定性。通过构建四邻域搜索策略,增强算法局部优化能力。实验结果表明,该方法能有效缩短半导体封测环节的最大完工时间。
关键词 :生产调度;半导体封装测试;多作业模式;孪生人工蜂鸟算法
中图分类号 :TP18
DOI:10.3969/j.issn.1004-132X.2024.02.010
开放科学(资源服务)标识码(OSID):
Scheduling in SAT in Multi-operation Mode Based on Artificial
Hummingbird Algorithm with Twin Population
WANG Hong 1,2 WU Lihui 3 CHEN Da 1,2 ZHANG Jie 2
1.College of Mechanical Engineering,Donghua University,Shanghai,201620
2.Institute of Artificial Intelligence,Donghua University,Shanghai,201620
3.College of Mechanical Engineering,Shanghai Institute of Technology,Shanghai,201418
Abstract : In order to solve the scheduling problem of SAT in multi-operation mode, an artificial hummingbird algorithm with twin population was proposed with the goal of minimizing the maximum completion time. The twin population mechanism was designed to improve the solution accuracy. By double decoding, twin population generation and cooperation methods, the searching space for solutions was expanded, the quality of the initial population solution was improved, and the diversity of population solutions was increased in optimization processes. By the bidirectional-guiding foraging strategy, the relationship between algorithm diversity and convergence was balanced, and algorithm stability was enhanced. By the strategy of four-variable neighbor searching, the local optimization ability of the algorithm was enhanced. The test results show that the proposed method may effectively shorten the maximum completion time of the SAT.
Key words : production scheduling;semiconductor assembly and test(SAT);multi-operation mode;artificial hummingbird algorithm with twin population(AHA-TP)
0 引言
半导体封装测试(semiconductor assembly and test, SAT)是半导体生产的重要环节,然而现阶段的SAT生产组织主要依赖调度人员的经验,具有较大局限性,因此急需兼顾求解时间与求解质量的方法,缩短SAT环节的加工周期,提高企业生产效益。对SAT的4道关键工序(贴片/装片、引线键合、塑封、电镀)的调度进行研究后,发现该调度问题具有多作业模式、设备工艺能力差异化、大规模等特点。SAT环节存在单机加工(引线键合)、批准备单处理加工(电镀)、批准备批处理加工(贴片/装片、塑封)三种作业模式,具有多作业模式的特点。引线键合与电镀工序中,各设备组均只能加工特定工艺范围的芯片且加工速度不一致,具有明显的工艺能力差异特点。SAT加工车间通常具有上千台加工设备,同时处理数十种产品、数百批芯片弹夹,具有大规模特点。多作业模式、设备工艺能力差异大、大规模等特点使SAT调度问题具有大规模解空间、可行解域扭曲畸形等特性,导致SAT调度问题优化困难。
SAT车间调度问题是典型的NP-hard问题 [1] ,国内外学者对其进行大量研究,提出了启发式规则方法、整数规划方法与智能优化方法。
姚丽丽等 [2] 提出一種结合逻辑约束与启发式调度规则的方法,实现了SAT产线调度问题的优化求解。CHEN等 [3] 设计了一种调度规则自动生成框架,解决了不同生产扰动下的调度问题。ZHANG等 [4] 利用调度规则解决了智能作业车间调度问题。以上启发式规则方法具有求解快的优点,但调度解的质量欠佳。
APPELO等 [5] 将混合整数规划方法用于半导体测试工序的调度优化。MENG等 [6] 提出一种新的混合整数规划模型用于解决分布式混合流水车间调度问题。QIU等 [7] 提出一种统一的混合整数线性规划(MILP)求解框架用于电力调度。以上整数规划方法虽能得到最优解,但求解较大规模问题的时间过长。
为解决求解质量欠佳与求解较慢的问题,借鉴自然界优化规律的智能优化算法被大量研究。WANG等 [8] 将合作迭代贪婪算法(CIG)用于解决分布式流水车间群的调度问题。WANG等 [9] 提出一种多子种群并行计算遗传算法(MSPCGA)来解决实际生产约束下的SAT调度问题。CHIU等 [10] 提出一种进化优化算法来解决SAT环节中具有灵活拆分规则的订单分配问题。牛昊一等 [11] 利用自适应樽海鞘群算法解决了柔性作业车间的调度问题。梁望等 [12] 通过两阶段智能优化算法解决了紧凑型带钢生产热轧调度问题。然而,现有面向SAT调度的智能优化算法具有求解效率不高等问题。
人工蜂鸟算法(artificial hummingbird algorithm, AHA)具有搜索效率高的特点,且该方法的寻优效率与优化效果优于遗传算法、粒子群算法、海鞘群算法等群智能优化算法 [13] 。然而,针对具有解空间规模大、可行解域扭曲畸形等特征的SAT调度问题,该方法存在收敛慢、易于陷入局部最优等 不足。
本文提出一种孪生人工蜂鸟算法(artificial hummingbird algorithm with twin population, AHA-TP)來解决SAT环节调度问题。首先,通过设计孪生种群机制,构建双解码、孪生种群生成与协作方法,提高蜂鸟种群初始解的质量,增加优化过程中种群解的多样性,提高求解精度。其次,通过构建双向引导觅食策略,加快孪生蜂鸟种群的收敛,平衡算法多样性与收敛性的关系。最后,设计四邻域搜索策略,避免孪生蜂鸟种群陷入局部最优搜索的瓶颈,提高算法的局部搜索优化能力,实现SAT问题的高效优化求解。
1 问题描述与建模
1.1 问题描述
SAT 环节的实际生产中, Lot 常作为调度的基本单元。本文所提多作业模式下的 SAT 调度问题描述如下:n个 Lot (工件)经过K个阶段的加工,每个 Lot 在不同阶段的作业模式不同,阶段k(k=1,2,…,K)有m k台设备。本文以最小化最大完工时间C max 为调度目标,作出以下假设: ①Lot在不同设备上的加工时间已知;②初始时刻,所有Lot与设备均准备就绪;③加工顺序固定,即所有Lot需按同一顺序加工;④每一阶段存在多台非等效的并行机,同一Lot在每阶段不同设备上的加工时间不同;⑤各个加工阶段中,Lot只能在一台设备上加工;⑥任何时刻,一个Lot只能在一台设备上加工;⑦加工一旦开始就不能 中断。
1.2 问题建模
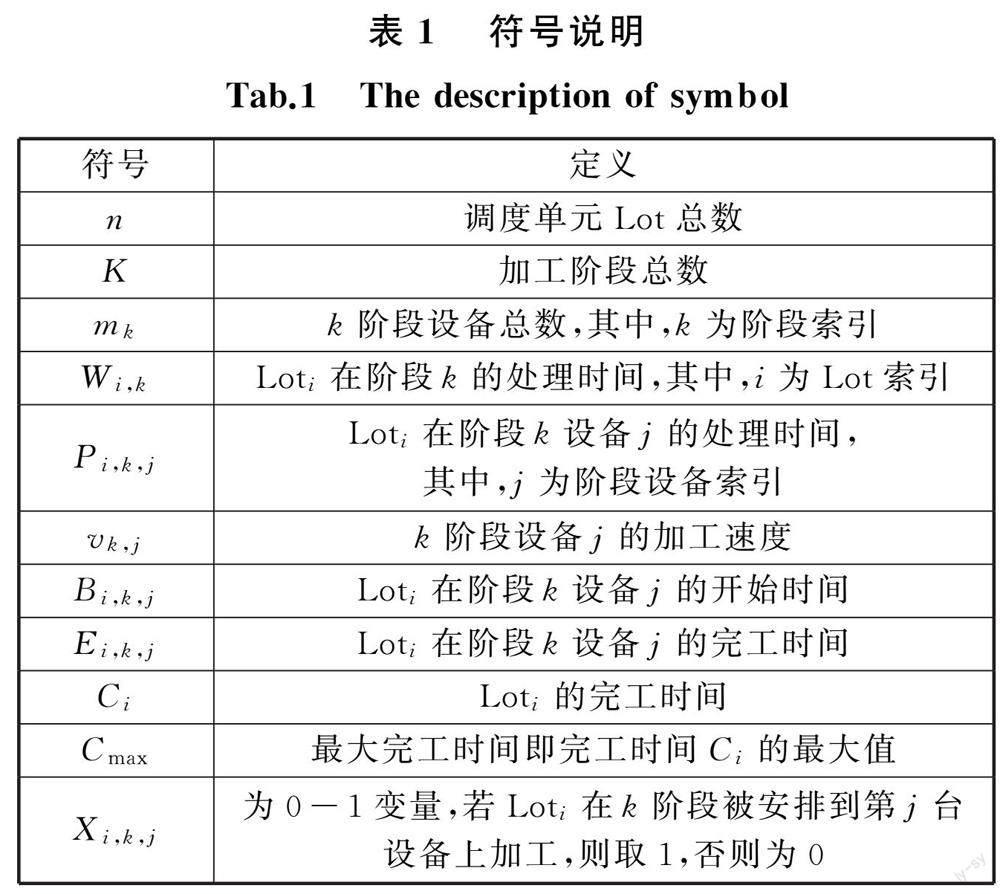
为数学描述 SAT 车间调度问题,定义表1所示的参数符号。
SAT 调度模型目标函数为
min C max = min ( max (C 1,C 2,…,C n)) (1)
模型约束条件如下:
E i,k,j ≤B i,k+1,j (2)
∑ m k j=1 X i,k,j =1 (3)
P i,k,j =∑ m k j=1 X i,k,j W i,k,j v k,j (4)
E i,k,j =B i,k,j +P i,k,j (5)
B i+1,k,j =E i,k,j (6)
式(1)为目标函数即最小化最大加工时间;式(2)表示 Lot i当前工序的开始时间在上道工序之后;式(3)表示 Lot i每阶段仅在一台设备上加工;式(4)表示 Lot i在各工序中的完工时间;式(5)表示 Lot i的完工时间为该 Lot i开始加工时间与该阶段处理时间之和;式(6)表示在k阶段设备j上的 Lot i加工结束时间为 Lot i+1 加工开始 时间。
2 基于AHA-TP的SAT调度方法
2.1 人工蜂鸟算法
人工蜂鸟算法模拟蜂鸟群在多维搜索空间的飞行,寻找待优化问题的最优解 [13] 。人工蜂鸟算法设计了“蜂鸟”的3种飞行方式(一维、多维和全维度的搜索),3种觅食方式(引导觅食、领域觅食、迁移觅食),以及访问表。引导觅食和领域觅食时,“蜂鸟”选择一种飞行方式来改变自身位置,从而获得新解,并根据新解的优劣情况更新原“蜂鸟”代表的解。迁徙觅食时,随机生成新解替换掉原“蜂鸟”种群中适应值最差的解。访问表用于指导“蜂鸟”在引导觅食过程中选择候选食物源,若迭代过程中寻找到更优秀的解,则“蜂鸟”在访问表中的被访问值会成为最大值,并在下次引导觅食过程中优先引导“蜂鸟”。每次觅食结束后,访问表会根据觅食类型与当前“蜂鸟”位置是否变得更优,进行不同方式的更新。
人工蜂鸟算法的流程如图1所示,具体步骤如下:
(1)种群初始化,即通过随机生成的方式得到初始种群。
(2) 种群个体随机进行引导觅食或领域觅食。
(3)若迭代次数为迁移系数MC的倍数,则进入步骤(4),否则进入步骤(5);
(4) “蜂鸟”种群进行迁徙觅食。
(5)若达到最大迭代次数,则结束迭代并输出最优解,否则进入步骤(2)。
2.2 AHA-TP算法框架
为对SAT调度问题进行高效求解,本文对AHA进行改进,提出了AHA-TP。AHA-TP的主要改进措施包括:①引入孪生种群机制,通过双解码、孪生种群生成与协作方法增大解的搜索空间,提高种群初始解的质量,增加优化过程中种群解的多样性,提高算法的求解精度;②实施双向引导觅食策略,通过设计最优引导觅食与访问引导觅食,平衡种群解的多样性与收敛性,增强算法的稳定性;③运用四邻域搜索策略,通过设计的4种邻域搜索方式增强算法的局部优化能力,加快算法收敛。AHA-TP的流程如图2所示,具体步骤如下:
(1)令迭代次数为I total ,种群数量为P size ,基于双解码策略生成孪生种群,完成种群初始化。
(2) “蜂鸟”个体基于双向引导觅食策略进行觅食。迭代次数I≤I total /2时,“蜂鸟”个体进行访问引导觅食,否则进行最优引导觅食。
(3)若迭代次数为P size /2的倍数,则进入步骤(4),否则进入步骤(5)。
(4)对孪生种群进行四邻域搜索。
(5)若迭代次数为P size 的倍数,则进入步骤(6),否则进入步骤(7)。
(6)对孪生种群进行孪生种群协作。
(7)若达到最大迭代次数,则结束迭代并输出最优解,否则进入步骤(2)。
2.3 编码
本文采用基于操作的编码方式 [14] ,将所有Lot的一种排序作为一个“蜂鸟”个体,Lot在“蜂鸟”个体中的位置序号为该Lot的加工顺序。
2.4 孪生种群机制
为扩大解搜索空间,提高种群初始解的质量与种群解在增加优化过程中的多样性,设计了双解码、孪生种群生成与协作方法,形成孪生种群 机制。
2.4.1 孪生种群双解码
本文设计的双解码策略包括正向解码与反向解码。
正解码从第一道工序开始,解码过程考虑2个子问题:①Lot在每阶段的加工顺序;②Lot在每阶段的设备分配。对于Lot加工顺序,解码采用“先进先出”(first in first out, FIFO)规则完成Lot序列的分配。对于设备分配,采取最先加工结束设备优先的原则即选择min( E i,K,j )对应的设备 j ,当存在多个相等的min( E i,K,j )时,正向解码选择序号更小的设备。
反向解码从第四道工序开始,解码过程与正解码方式相似,但有两点不同:①反向解码过程中,可将第四工序(该工序为批准备单处理加工模式)按照单机加工模式进行解码,调度结果依旧满足批准备单处理加工模式的约束;②对于设备分配,当存在多个相等的min( E i,K,j )时,反向解码选择序号更大的设备。图3为编码{2,7,8,3,4,6,9,10,5,1}采用两种解码方式得到的甘特图。
2.4.2 孪生种群生成
本文结合双解码提出一种基于孪生种群的初始化方法,如图4所示,图中,上标p表示正向解码,n表示反向解码。首先,基于随机数方式生成 P size 个“蜂鸟”个体;其次,对所有初始化个体进行正解码,并按照适应值排序;然后,通过间隔筛选个体的方式,抽取出排序靠前的若干个体构建正孪生种群。同理,对随机种群进行反解码,按适应度值进行排序,并通过间隔筛选获得反孪生种群。最后,合并正反孪生种群,得到孿生种群。
2.4.3 孪生种群协作
为增加种群解在优化过程中的多样性,算法设计了孪生种群协作策略。如图5所示,该策略包括孪生种群解码逆序、临时种群解码适应值排序、交叉协作等,具体步骤如下。
(1)孪生种群解码逆序。先对正孪生种群P p 0、反孪生种群P n 0进行适应值排序,再对排序后的种群个体进行解码,并对得到的编码进行逆序操作,获得末阶段、初阶段的 Lot 编码,形成临时反孪生种群P n 1、正孪生种群P p 1。
(2) 临时种群解码适应值排序。对P p 1、P n 1分别进行正反解码,并根据适应度值大小进行排序。
(3)交叉协作。从P p 1中选出排序前α的个体替换掉P p 0中排序后α的个体,从P n 1中选出排序前α的个体替换掉P n 0中排序后α的个体,形成新的正孪生种群P p 2、反孪生种群P n 2。
2.5 双向引导觅食策略
为平衡种群的多样性与收敛性,并增强算法的稳定性,本文设计了双向引导觅食策略,包括访问引导觅食与最优引导觅食。当迭代次数I≤I total /2时,“蜂鸟”个体B 0进行访问引导觅食,由访问表中最大引导值对应的“蜂鸟”B G 进行引导;当迭代次数I>I total /2时,进行最优引导觅食,即让当前适应值最小的“蜂鸟”个体B mfit 引导“蜂鸟”个体B 0。觅食结束后,生成新的“蜂鸟”个体B 1与B 2,比较B 0、B 1与B 2的适应值,将适应值最小的“蜂鸟”个体替换B 0,并更新访问表。访问表更新规则参考文献[13]。3种飞行方式对应的引导觅食如图6所示。
2.6 四邻域搜索策略
为增强算法的局部优化能力,本文设计了四邻域搜索策略,即每经过P size /2次迭代,对正反孪生种群适应值排序前N S 的个体进行变邻域搜索,每种邻域搜索方式针对种群个体进行N nb 次搜索。
变邻域搜索按照搜索范围从大到小的顺序,依次进行多点互换、反转逆序、插入与两点互换。多点互换:选择3~n个位置的编码进行随机排序。反转逆序:随机取出一段编码进行逆序。插入:随机取两个位置,将后一位置的编码插入至前一位置的编码所在位置,原编码依次后退一位。两点互换:随机抽取两个位置更换编码。四邻域搜索策略如图7所示。
3 实验验证
为验证AHA-TP求解多作业模式下SAT调度问题的有效性,基于某半导体封测企业数据,设计了验证案例进行实验。实验验证分为实验设计、算法参数实验、算法改进有效性实验和案例测试四个环节。
3.1 实验设计
根据某半导体封测工厂实际生产数据,设计了三种规模的案例,如表2所示,其中,J i、M i分别为 Lot 数量和四阶段(贴片/装片、引线键合、塑封和电镀)设备数量。考虑贴片/装片、塑封批处理加工特性,设定两阶段加工时间为W 1=60,W 3=120,相对加工速度为v 1,v 3=1.00(W 1、W 3分别为第一阶段与第三阶段的加工时间,v 1、v 3分别为第一阶段与第三阶段的相对加工速度);考虑引线键合、电镀单处理加工特性,设定第二阶段与第四阶段的加工时间为W 2∈[60,90],W 4∈[45,60],相对加工速度v 2,v 4∈{1.00,1.25, 1.50}, 具体的加工时间和相对加工速度为区间或集合内均匀分布的随机数。 实验环境为Win10系统,CPU为i5-12400f、内存为16GB,采用python3.6编程,编译器为PyCharm2021。
3.2 算法参数实验
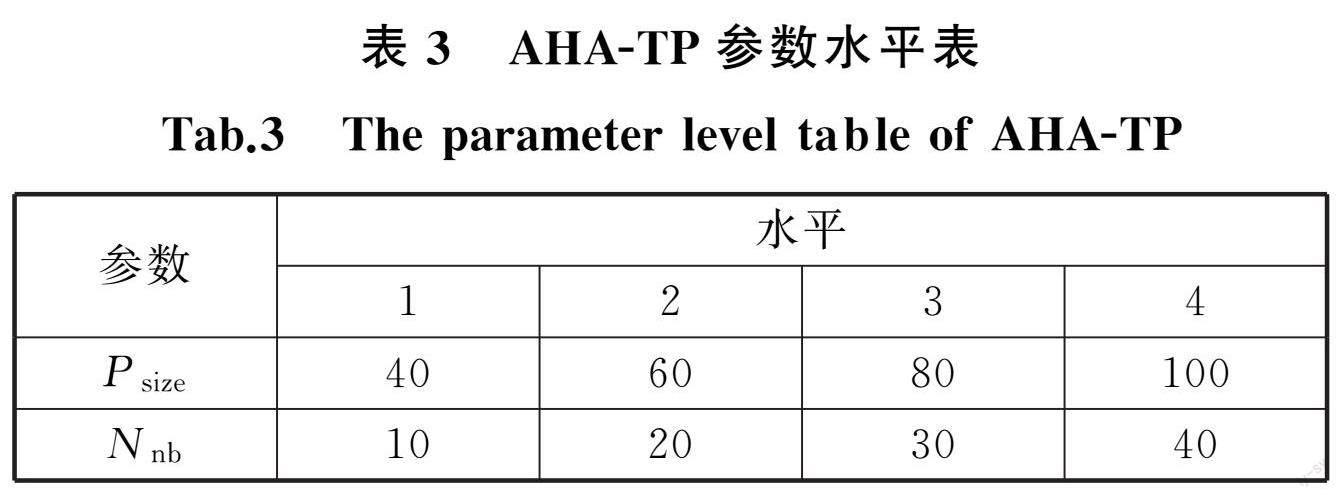
参数设置会对 AHA-TP 性能产生较大影响,其中的关键参数为种群数量P size 和变邻域搜索的次数N nb 。 AHA-TP 参数水平的取值见表3。基于中规模案例数据确定P size 与N nb ,该案例中的 Lot 数量为30,四阶段设备数量{3,6,6,6}。对每一组参数组合独立运行算法10次,每次进行2000次迭代,以最小适应值的均值为评价指标。
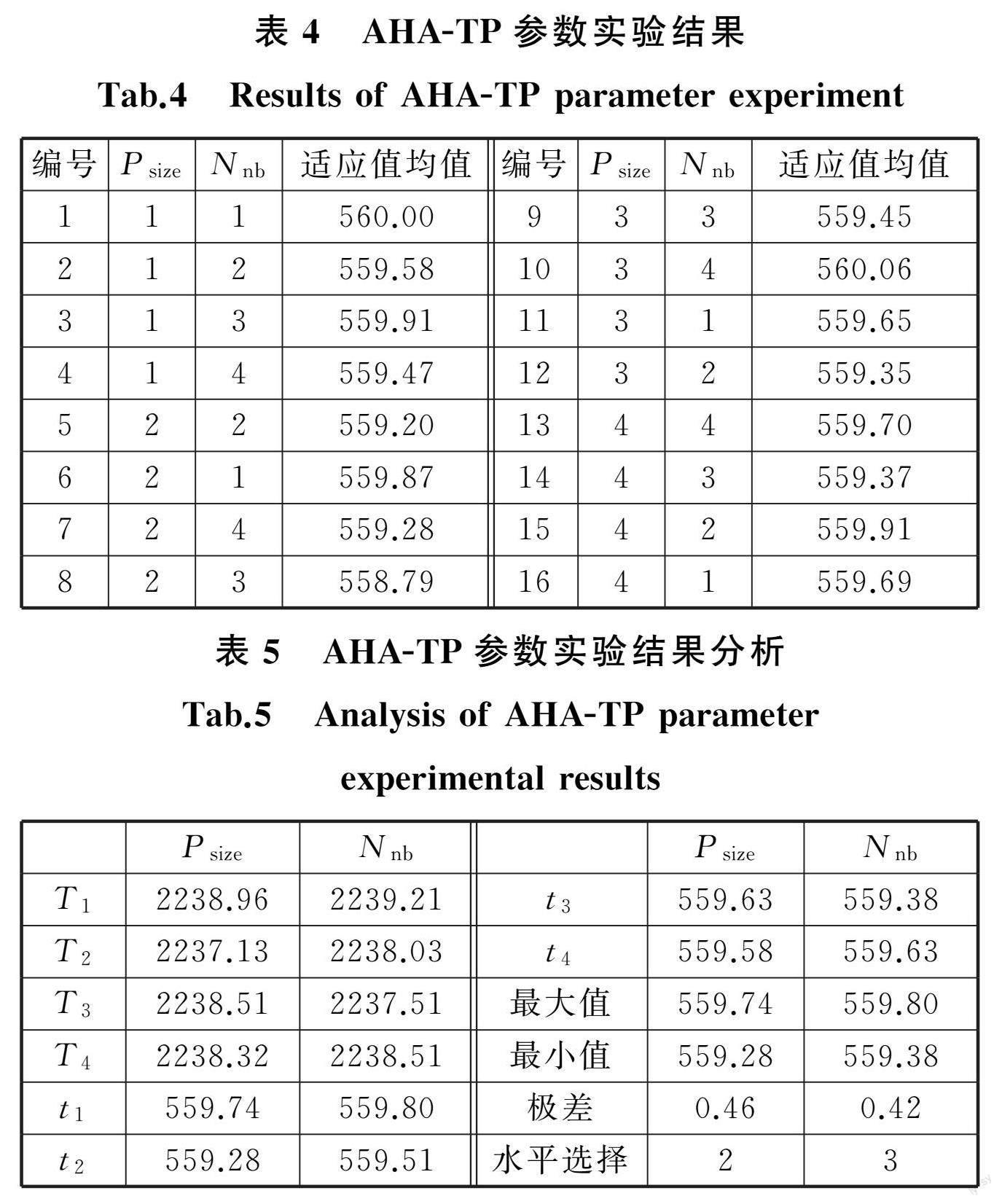
AHA-TP 参数实验的结果如表4所示,对实验结果进行分析处理,得到表5所示的分析结果。表5中,T 1~T 4为两参数对应水平的适应值均值之和,t 1~t 4为两参数对应水平的适应值均值的平均值。 对比表5中的极差可知,P size 对算法效果的影响程度大于N nb 的影响。由表5可得,P size 为水平2、N nb 为水平3时, AHA-TP 的效果最好,即 AHA-TP 设定的最佳参数为P size =60,N nb =30。
3.3 算法改进有效性实验
为验证AHA-TP改进策略的有效性,基于中等规模算例将AHA-TP与AHA-1、AHA-2、AHA-3、AHA-4进行对比,其中,AHA-1为AHA-TP去掉孪生种群机制中的孪生种群生成方法的优化算法,AHA-2为AHA-TP去掉孪生种群机制中的孪生种群协作方法的优化算法,AHA-3为AHA-TP去掉双向引导策略的优化算法,AHA-4为AHA-TP去掉四邻域搜索策略的优化算法。
由表6可得如下结果:①AHA-TP与AHA-1的比较结果表明,孪生种群生成方法使适应值的均值差(均值与已发现最小值531.00之差)减小84%,标准差减小60%,增大了搜索空间,提高了算法求解精度;②AHA-TP与AHA-2的比较结果表明,孪生种群协作方法使适应值均值减小37%,标准差减小41%,增加了优化过程中种群解的多样性,避免算法陷入局部最优;③AHA-TP与AHA-3的比较结果表明,双向引導觅食策略设计使适应值均值减小32%,标准差减小49%,平衡了算法的收敛性与多样性,增强了算法的稳定性;④AHA-TP与AHA-4的比较结果表明,四邻域搜索策略设计使适应值均值减小72%,标准差减小60%,最优值迭代数的均值减小17%,增强了算法的局部优化能力。
3.4 案例测试
为验证AHA-TP在多作业模式下SAT调度问题上的有效性,将其与AHA和改进遗传算法(improved genetic algorithm, IGA)进行比较。对比指标包括最大加工完工时间(适应值)的最小值、均值、均值差(均值与最小值之差)、最大值、最大值差(最大值与最小值之差)、标准差。为减小随机性对实验的影响,3个算法在每个案例上运行15次,迭代次数为2000。为保证实验的有效性,AHA和IGA的种群规模与AHA-TP一致,均为60。IGA的交叉概率和变异概率分别设为0.9和0.1,采用随机多点交叉操作和两点交换变异操作。AHA与IGA采用正向解码,通过随机数的方式生成初始种群。实验结果如表7、表8所示。
由表7、表8可知:①AHA-TP在小规模案例中的最小值、均值与最大值的平均值分别为 546.86、 546.88、547.20,在中规模案例中的最小值、均值与最大值的平均值分别为538.56、 540.43、 542.74,在大规模案例中的最小值、均值与最大值的平均值分别为594.44、596.50、 598.60, 均优于AHA与IGA,说明AHA-TP的求解精度优于AHA与IGA;②AHA-TP在小规模案例中的均值差与最大值差的平均值分别为 0.02、 0.34,在中规模案例中的均值差与最大值差的平均值分别为1.87、4.18,在大规模案例中的均值差与最大值差的平均值分别为2.06、4.16,均优于AHA与IGA;③AHA-TP在小、中、大规模案例中的标准差平均值为0.08、1.09、1.12,在中规模、大规模案例中优于AHA,而稍逊于IGA,说明AHA-TP的稳定性优于AHA,而稍逊于IGA。图8中,AHA-TP与AHA的箱型图中位线均低于IGA, 且相对于AHA,AHA-TP解的最大值与最小值之差更小, 即算法求解精度与稳定性得到提高。综上所述,AHA-TP在解决SAT调度问题上具有良好优化效果,能有效最大完工时间。
4 結语
本文研究了以最小化最大完工时间为目标的多作业模式下SAT调度问题,提出了基于AHA-TP的SAT调度方法。该方法主要改进如下:①设计了孪生种群机制策略,完成AHA-TP种群的初始化,扩大了解的搜索空间,提高了初始种群解的质量,在优化过程中增加了解的多样性;②改进了AHA-TP中的双向引导觅食寻优策略,平衡了算法多样性与收敛性,增强了算法的稳定性;③AHA-TP增加了四邻域搜索策略,增强了算法局部优化能力。案例实验结果证明了AHA-TP的性能,可有效缩短SAT调度问题的最大完工时间。在SAT调度实际应用中,AHA-TP可与半导体封测车间MES系统紧密结合,从MES获取数据,计算并反馈优化结果给MES,实现生产线的调度优化。
在未来研究中,为贴近实际生产情况,可考虑包括换机时间、资源约束等更多约束,以及总拖期时间、总能耗、总排放等其他性能指标。
参考文献 :
[1] CHEN Jianbin, PENG Jiayu, LIN D K J. A Statistical Perspective on Non-deterministic Polynomial-time Hard Ordering Rroblems:Making Use of Design for Order-of-addition Experiments[J]. Computers & Industrial Engineering, 2021, 162:107773.
[2] 姚丽丽,史海波,刘昶. 半导体封装测试生产线排产研究[J]. 自动化学报, 2014(5):892-900.
YAO Lili, SHI Haibo, LIU Xu. Research on Scheduling in Semiconductor Assembly and Test Manufacturing[J]. Acta Automatica Sinica, 2014(5):892-900.
[3] CHEN Xiaowu, JIANG Guozhang, XIAO Yongmao, et al. A Hyper Heuristic Algorithm Based Genetic Programming for Steel Production Scheduling of Cyber-physical System-oriented[J]. Mathematics, 2021, 9(18):2256.
[4] ZHANG Liping, HU Yifan, WANG Chuangjian, et al. Effective Dispatching Rules Mining Based on Near-optimal Schedules in Intelligent Job Shop Environment[J]. Journal of Manufacturing Systems, 2022, 63:424-438.
[5] APPELLO D, LAURINO M, PRANZO M. A Mathematical Model to Assess the Influence of Parallelism in a Semiconductor Back-end Test Floor[C]∥2017 International Test Conference in Asia (ITC-Asia). Taipei, 2017:138-143.
[6] MENG Leilei, GAO Kaizhou, REN Yaping, et al. Novel MILP and CP Models for Distributed Hybrid Flowshop Scheduling Problem with Sequence- dependent Setup Times[J]. Swarm and Evolutionary Computation, 2022, 71:101058.
[7] QIU Haifeng, GOOI H B. A Unified MILP Solution Framework for Adaptive Robust Scheduling Problems with Mixed-Integer Recourse Objective[J]. IEEE Transactions on Power Systems, 2022, 38(1):952-955.
[8] WANG Yuhang, HAN Yuyan, WANG Yuting, et al. Intelligent Optimization under the Makespan Constraint:Rapid Evaluation Mechanisms Based on the Critical Machine for the Distributed Flowshop Group Scheduling Problem[J/OL]. European Journal of Operational Research, 2023[2023-10-23]. https:∥doi.org/10.1016/j.ejor.2023.05.010.
[9] WANG H K, LIN Y C, LIANG C J, et al. Multi-subpopulation Parallel Computing Genetic Algorithm for the Semiconductor Packaging Scheduling Problem with Auxiliary Resource Constraints[J]. Applied Soft Computing, 2023, 142:110349.
[10] CHIU C C, LAI C M, CHEN C M. An Evolutionary Simulation-optimization Approach for the Problem of Order Allocation with Flexible Splitting Rule in Semiconductor Assembly[J]. Applied Intelligence, 2023, 53(3):2593-2615.
[11] 牛昊一,吴维敏,章庭棋, 等.自适应樽海鞘群算法求解考虑运输时间的柔性作业车间调度[J].浙江大学学报(工学版),2023,57(7):1267-1277.
NIU Haoyi, WU Weimin, ZHANG Tingqi, et al. Adaptive Zunhei Scabbard Swarm Algorithm for Flexible Job Shop Scheduling Considering Transportation Time[J]. Journal of Zhejiang University (Engineering Edition), 2023,57(7):1267-1277.
[12] 梁望,钱斌,胡蓉, 等.两阶段智能优化算法求解紧凑型带钢生产热轧调度问题[J/OL].计算机集成制造系统, 2023[2023-10-23]. http:∥kns.cnki.net/kcms/detail/11.5946.TP.20230801.1648.007.html.
LIANG Wang, QIAN Bin, HU Rong et al. A Two-stage Intelligent Optimization Algorithm for Solving the Hot Rolling Scheduling Problem of Compact Strip Production[J/OL]. Computer Integrated Manufacturing System, 2023[2023-10-23]. http:∥kns.cnki.net/kcms/detail/11.5946.TP.20230801.1648.007.html.
[13] ZHAO Weiguo, Wang Liying, MIRJALILI S. Artificial Hummingbird Algorithm:a New Bio-inspired Optimizer with Its Engineering Applications[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 388:114194.
[14] 崔琪,吴秀丽,余建军. 变邻域改进遗传算法求解混合流水车间调度问题[J]. 计算机集成制造系统, 2017, 23(9):1917-1927.
CUI Qi, WU Xiuli, YU Jianjun. Improved Genetic Algorithm Variable Neighborhood Search for Solving Hybrid Flow Shop Scheduling Problem[J]. Computer Integrated Manufacturing System, 2017, 23(9):1917-1927.
( 編辑 张 洋 )
作者简介 :
王 洪 ,男,2000年生,硕士研究生。研究方向为复杂制造系统调度、制造大数据分析。E-mail:2221044@mail.dhu.edu.cn。
张 洁 (通信作者),女,1963 年生,教授、博士研究生导师。研究方向为大数据驱动的智能制造系统、制造系统的建模仿真调度,发表论文100余篇。E-mail:mezhangjie@dhu.edu.cn。

