测量噪声下的高超声速飞行器组合观测鲁棒控制

张睿，李世华，魏振岩，许斌

（1.东南大学自动化学院，南京 210096；2.西北工业大学自动化学院，西安 710129；3.北京机电工程研究所，北京 100074）

0 引言

高超声速飞行器（Hypersonic flight vehicle，HFV）能够以马赫数超过5 的高速度巡航飞行，在民用和军事领域发挥着至关重要的作用，越来越受到人们的重视。当前已经成功进行了X-43A、X-51A 和猎鹰HTV-2 等型号的试飞验证。HFV 的机身与推力系统设计呈现高度一体化，机身外形纤细，材料轻薄，气动、推力、弹性三者之间的耦合突出。文献［1-2］分别给出了HFV 锥体加速器模型和曲线拟合得到的面向控制模型。考虑到飞行环境、气动参数和外界扰动的大范围变化，HFV 控制过程中存在扰动和噪声干扰。

为了使HFV 在各种干扰下获得良好的跟踪性能，已有大量的先进控制方案研究。文献［3-4］将面向控制的HFV 纵向通道模型分解为速度子系统和高度子系统，分别设计控制器实现参考轨迹跟踪。其中，针对速度子系统，设计了鲁棒自适应控制器。针对高度子系统，提出了动态逆控制，避免了传统反步控制的“计算爆炸”问题。文献［5］在反馈线性化控制的框架下，采用滑模控制来提高HFV控制系统的鲁棒性。文献［6］分别设计了有限时间终端滑模控制和高阶滑模控制以获得更快的跟踪误差收敛速度和更高的控制精度。考虑HFV 大包络飞行时复杂飞行环境导致的系统未知动力学，文献［7-9］分别采用神经网络对未知非线性动力学进行逼近，并将逼近结果进一步前馈到控制器中，以获得更高的跟踪控制精度。考虑风等外部干扰引起的扰动，当扰动存在上界时，文献［10］设计了扰动观测器。然而，上述研究忽略了实际HFV 系统中攻角、航迹角等系统状态难以测量的问题，所设计的控制器难以工程实现。针对这一问题，文献［11］同时考虑无法测量的状态和干扰，将不确定性和外部干扰视为一个新的系统状态，与原有系统状态方程联立，设计扩张状态观测器（Extended state observer，ESO）同时对不可测系统状态、不确定和干扰构成的集总不确定进行估计。文献［12-13］在此基础上进一步面向HFV 控制系统提出了高增益观测器和变增益观测器，以提高ESO 的收敛速度和估计精度。文献［14］研究了有限时间观测器，以实现更快的状态估计。

值得注意的是，在上述工作中，HFV 控制器都是在假设系统无噪声的情况下设计的。这种假设是不现实的。由于模型构建误差、极端飞行环境以及飞行器超高速飞行产生的电磁干扰等因素将影响传感器的测量精度，系统状态中必然存在测量噪声。如果将被噪声污染的系统状态直接应用到控制器设计中，会导致跟踪性能下降，甚至失控。因此，必须在控制器设计中降低噪声的影响。文献［15］利用二阶命令滤波器来处理系统噪声。文献［16］提出了线性高斯二次型（Linear quadratic Gaussian，LQG）/回路传递恢复（Loop transfer recovery，LTR）控制器，实现噪声影响下的HFV 高精度全通道姿态控制。然而，上述HFV 控制研究虽然在控制器设计中增加了噪声处理环节，却忽略了外部干扰的影响，导致控制系统抗噪能力增强，抗扰能力有限。同时考虑噪声和外部干扰的影响，文献［17］面向线性系统提出了ESO和Kalman滤波的组合观测策略，但是该方法不仅要求被控对象为线性系统，更要求传感器测量噪声的统计特性提前已知，这一点实际工程中难以保证，在呈现非线性且面临复杂多变飞行环境的HFV 控制系统中更是完全不能实现。如何获取不受干扰和测量噪声影响的系统状态，并基于该系统状态设计HFV 控制器实现对高度参考信号和速度参考信号的高精度鲁棒跟踪仍待解决。

针对HFV 大包络飞行时，飞行器模型和传感器测量受风干扰和噪声影响，导致控制系统性能变差甚至失稳的问题，本文提出了一种基于状态观测的鲁棒控制策略。首先，采用小扰动线性化理论，推导HFV 的线性纵向通道模型；其次，基于该模型设计“AKF+ESO”组合状态观测器，在未知测量噪声及外部干扰的影响下准确重构系统状态；再次，基于“AKF+ESO”估计的系统状态，设计LQG控制器实现HFV 对高度参考信号和速度参考信号的高精度跟踪；最后，仿真验证本文HFV 组合观测控制策略的有效性。

1 高超声速飞行器动力学模型

1.1 高超声速飞行器的纵向通道模型

考虑风场干扰的影响，HFV 的纵向通道动力学模型为［3-4］：

式中：V，h，γ，α，q分别为速度、高度、航迹角、攻角、俯仰角速率；m为飞行器质量；g为重力加速度；Myy，Iyy分别为俯仰转动力矩和俯仰转动惯量；dγ(t)，dq(t)为风场造成的外部干扰；T，D，L分别为飞行器发动机推力、阻力、升力，并且满足：

1.2 动力学模型线性化

采用小扰动线性化理论线性化动力学模型（1）。在平衡点(Ψ0，u0)处进行泰勒展开，保留泰勒展开一次项，忽略高阶项，动力学模型（1）可改写为如下线性时不变状态方程，即：

式（5）和式（6）中，系统状态向量选取为平衡点处的系统状态Ψ0，系统输入选取为平衡点处的输入量u0，且：

模型（3）的其他参数为：

假设采样时间为Ts，采用zero-order-hold（ZOH）方法对HFV 线性动力学模型（3）进行离散化处理。记Ψk=Ψ(kTs)，uk=u(kTs)，ξk=ξ(kTs)，yk=y(kTs)，=(kTs)，k为当前时刻，动力学模型（3）离散化后得：

式中：A=I5×5+AΨTs，B=BΨTs，Bξ=BξdTs。

考虑测量噪声的影响，离散动力学模型（9）可重新写为：

式中：ωk∈R5为测量噪声。

假设2.定义ωk为高斯白噪声，定义扰动估计误差为过程噪声vk=Bξξk-，且vk为高斯白噪声，满足：

注1.线性动力学模型（3）中的矩阵AΨ和BΨ为非线性动力学函数fi在平衡点(Ψ0，u0)处的雅可比矩阵，均为时不变的常值矩阵。这种在平衡点处展开的HFV 小扰动线性化方法在文献［16］中得到了详细论证。

2 基于AKF和ESO的状态组合观测

考虑被噪声污染的测量信号如果直接用于HFV 控制可能激发执行器额外的高频控制量，降低控制性能甚至导致系统失控，必须在控制器设计中使用不受噪声和干扰影响的系统状态。本节提出了“AKF+ESO”的状态组合观测方法，在统计特性未知的测量噪声和外部干扰影响下获取准确的系统状态估计。

面向HFV 离散动力学模型中统计特性未知的测量噪声，设计AKF 实时估计噪声的统计特性并获取不受噪声影响的系统状态，随后将降噪后的系统状态输入ESO 实现对外部干扰的估计。值得注意的是，ESO估计的外部干扰又被引入了AKF，以提升AKF 的抗干扰能力。这种自增强拓扑使组合观测结构能够在外部干扰、噪声并存的环境下精确地重构系统状态。

考虑系统（10），设计AKF为：

基于扩张状态方程（11），设计ESO为：

为了提升ESO 的抗噪能力，将式（17）中的yk替换为AKF 估计预测的系统输出，因此，式（17）可重新写为：

定义AKF估计误差为：

定义ESO估计误差为：

进一步计算可得：

在假设1情形下，存在正常数Δm使得‖Δk‖≤Δm。

注2.选取合适的平衡点(Ψ0，u0)，使得(A，B)可控，(A，C)可观，则可推导得到()可观。此时，通过调整增益Kk和Ks可以实现Ηk的任意极点配置，使得状态估计误差有界。

注3.式（16）同时给出了和的更新律。然而，在实际系统中难以同时实现两者的在线估计，通常仅更新其中一个噪声统计特性。

注4.本文设计的“AKF+ESO”组合观测结构可在测量噪声及外部干扰存在的情形下，准确重构不可测系统状态。已有AKF和ESO与“AKF+ESO”相比，其缺陷在于：AKF 虽能降低噪声影响，但受外部干扰影响不能准确重构系统状态；传统ESO 可重构系统状态，但为了获取更快收敛速率，必须设置极大的观测增益，这导致测量噪声被放大，系统状态估计精度降低。

3 LQG控制器设计

基于“AKF+ESO”组合观测的系统状态，本节设计LQG 控制器实现对高度参考信号和速度参考信号的鲁棒跟踪，具体方案如图1所示。

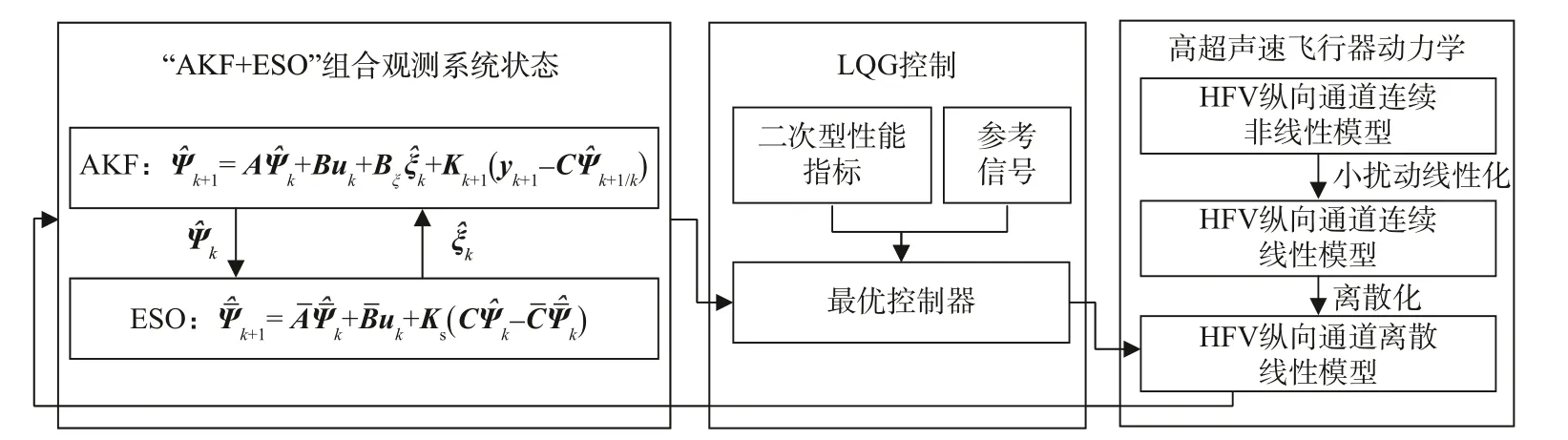
图1 基于“AKF+ESO”组合观测的HFV鲁棒控制策略Fig.1 Robust control strategy of HFV based on AKF+ESO combined observation

定义有限时域二次型性能指标为

式 中：FL=02×2；QL∈R2和RL∈R2为正定对称矩阵。

使目标函数J取最小值的最优控制器设计为：

式中：控制增益KΨ设计为

其中，PL通过计算如下黎卡提矩阵方程可得：

θk设计为

式中：Φk设计为

Kξ设计为

将控制器（32）代入动力学方程（10），得：

联立式（34）和式（23）可得增广矩阵方程为

注5.由于“AKF+ESO”的干扰估计误差有界，且Δk在假设1 下有界，给定参考信号和参数矩阵B，QL和RL后，Ξk有界。

注6.A，B，QL和RL给定后，控制增益KΨ为式（27）计算得到的定常矩阵，系统（36）的极点随之确定。根据文献［18］可知，由于QL和RL为正定对阵矩阵，系统（36）渐近稳定。

注7.控制增益KΨ的设计与QL和RL取值有关。QL和RL的选取对系统动态性能有影响。QL越大，系统跟踪精度越高；RL越大，uk越平稳。

4 仿真分析

记本文提出的基于“AKF+ESO”组合观测的LQG 控制方法为“本文方法”，为了验证其抗噪抗干扰能力，将之与文献［19］提出的LQR 控制（记为“对比方法”）在仿真中作对比。

选取HFV 的初始配平状态为Ψ0=[V0，h0，γ0，α0，q0]T，其中V0=2 392.68 m/s，h0=26.212 km，γ0=0°，α0=3.69°，q0=0（°）/s；u0=[γΦ0，δe0]T且γΦ0=0.1，δe0=0.1。忽略极小量，计算配平状态下HFV线性动力学模型（3）的参数为：

选取外 部干扰为dγ(t)=-10-3，dq(t)=-10-5。AKF 和ESO 的系统初始状态初值与配平状态选取一致。设置AKF 参数为b=0.998。选取AKF 噪声相关矩阵的初值为：

设置ESO增益为：

高度和速度参考信号分别增加152.4 m 和30.48 m/s 的阶跃信号，且该阶跃信号通过以下滤波器：

式中：ωh1=0.5；ωh2=0.1；ωV1=0.3；ωV2=0.2；ςh=0.7；ςV=0.7。

设置二次型性能指标函数的参数为FL=02×2，QL=diag(1，1)，RL=diag(1，0.01)。

仿真结果如图2～4所示。图2和图3分别给出了两种鲁棒控制策略下的高度、速度跟踪曲线及跟踪误差曲线，由图可知相较于文献［19］提出的LQR控制，本文提出的方法不仅具有良好的抗噪能力，且跟踪精度更高。这是由于“AKF+ESO”组合观测结构结合了Kalman 滤波器和ESO 的优点，Kalman滤波器具有抗噪能力，而ESO 具有干扰估计能力。图4 给出了“AKF+ESO”组合观测系统状态的误差，包括速度估计误差、高度估计误差、航迹角估计误差、攻角估计误差、俯仰角速率估计误差。由图4可知，在外部干扰和噪声影响下，系统状态得到了有效估计。由此可证，本文提出的HFV 组合观测控制策略可在噪声及外部干扰影响下实现准确的系统状态估计，进而实现对参考速度和参考高度信号的鲁棒跟踪。

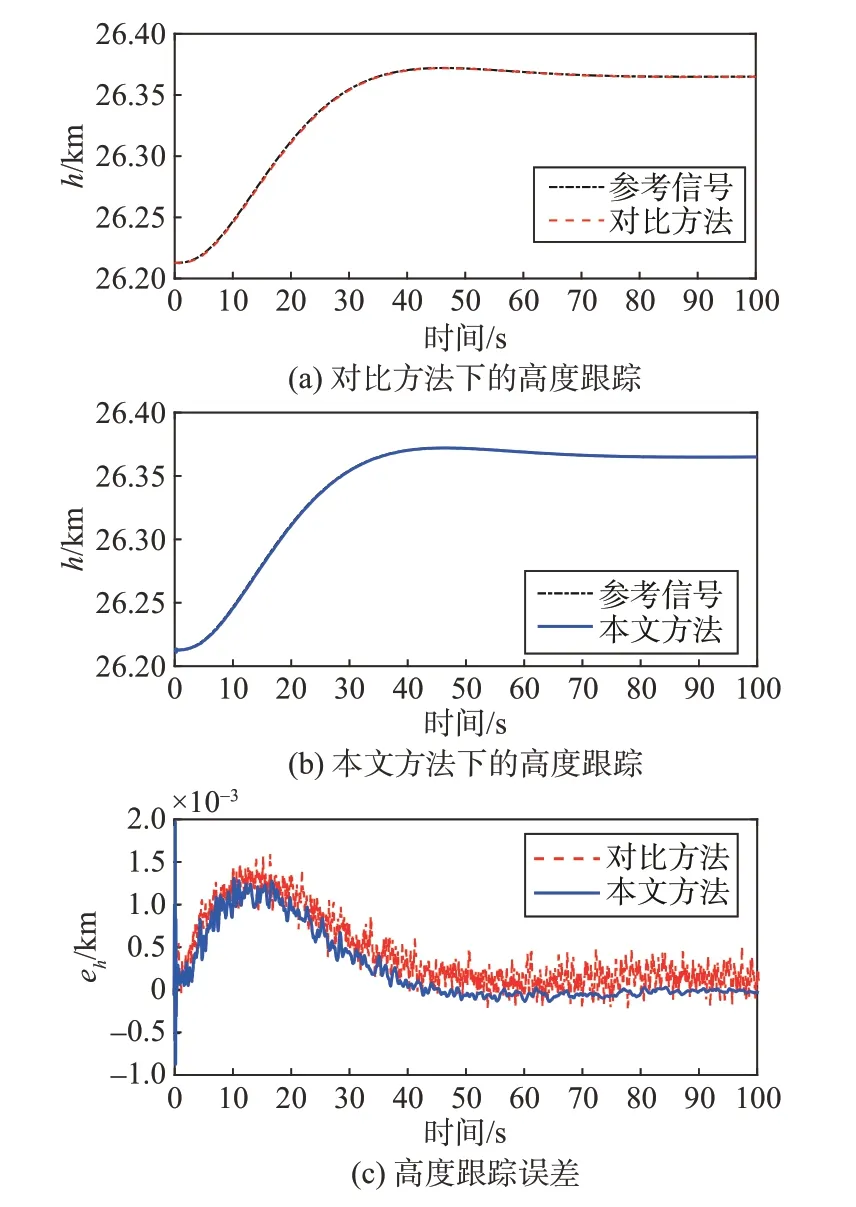
图2 高度跟踪Fig.2 Altitude tracking

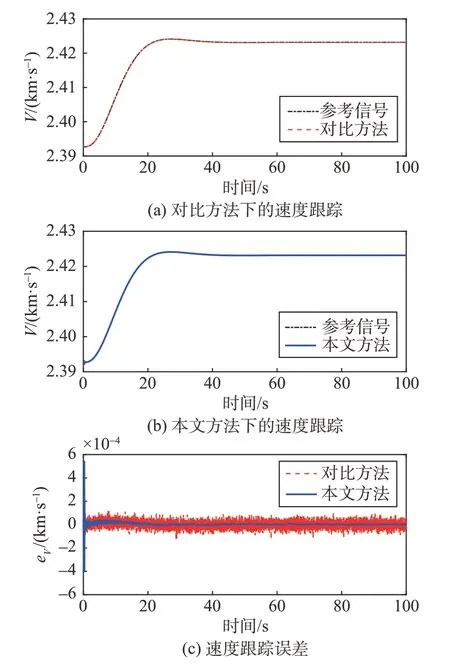
图3 速度跟踪Fig.3 Velocity tracking

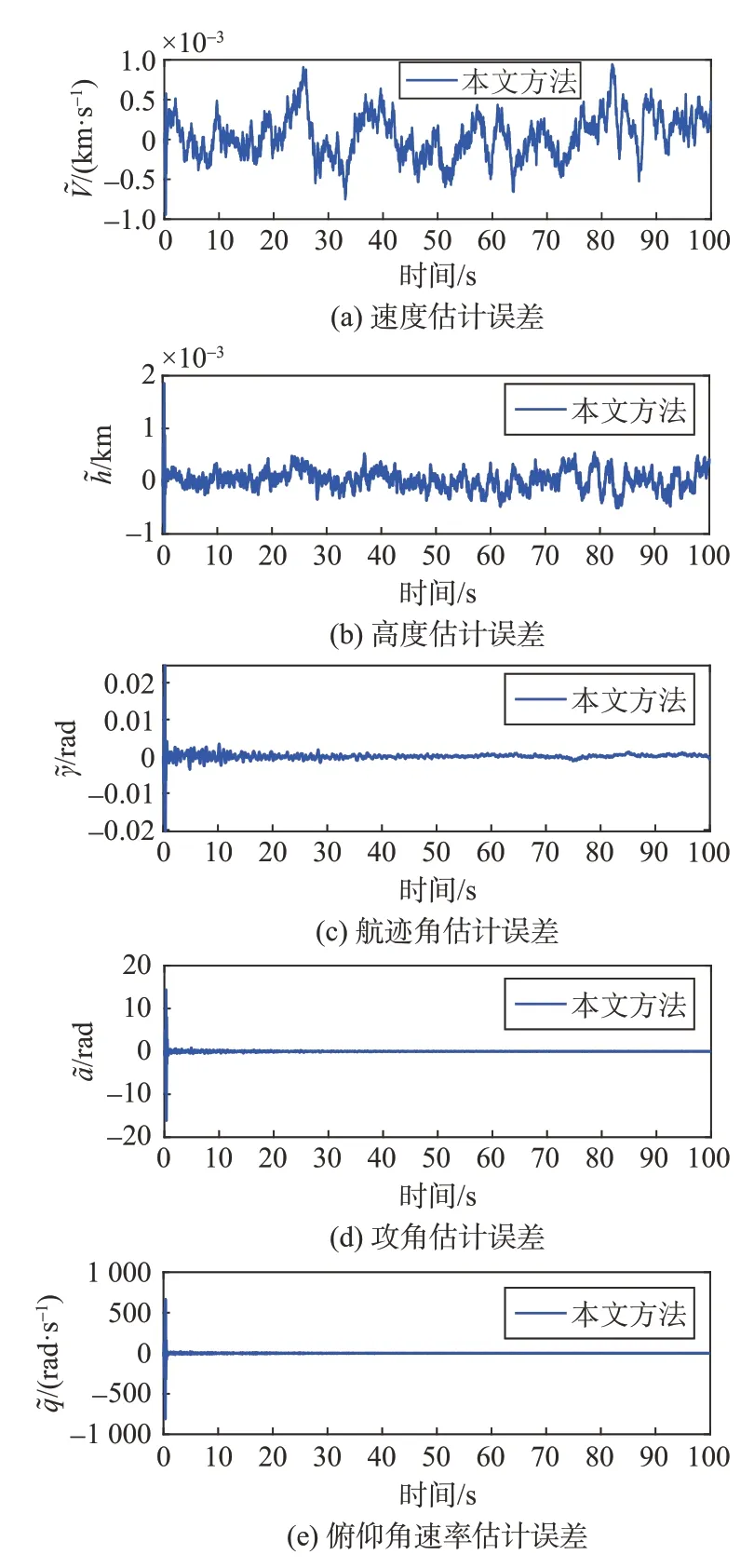
图4 “AKF+ESO”组合观测的系统状态Fig.4 Combined observation of system states under “AKF+ESO”

5 结论

本文针对系统状态受测量噪声和风场等外部干扰影响导致控制性能衰减的问题，提出基于“AKF+ESO”组合观测的LQG 控制策略。综合利用AKF 降噪和ESO 估计外部干扰，通过自增强拓扑结构精确重构系统状态，提升HFV 鲁棒控制精度。文中给出的仿真实例说明了该方法的有效性。