面向动态禁飞区的自适应触角探测机动制导方法

杨浩东，王剑颖，吴志刚，刘佳琪，梁海朝

（1.中山大学航空航天学院，深圳 518106；2.北京航天长征飞行器研究所，北京 100076）

0 引言

高超声速飞行器再入过程具有强耦合、非线性、快时变的动力学特征［1-2］，为了使高超声速飞行器能够按预定任务精确到达目标再入点，近年来针对高超声速飞行器制导方法的研究已经成为领域内的学术热点。经典的再入制导重点考虑在动压、过载和热流约束下，确保高超声速飞行器顺利抵达目标点，其核心在于通过设计飞行器再入走廊，同时将再入约束转化为走廊上下界，再通过飞行走廊内的轨迹规划［3-5］及预测校正［6-8］实现由初始再入点到目标点的再入制导。

随着高超声速飞行器作战任务的多元化和复杂化，考虑由于地形、地缘政治、防空拦截等产生的禁飞区域约束，面向禁飞区规避的高超声速飞行器再入制导方法已成为高超声速技术发展的重要趋势。学者们在已有的高超声速飞行器横向制导的基础上进行改进，提出了动态方位角偏差走廊制导方法［9-12］，如文献［11］将禁飞区边界与飞行器的连线引入航向角偏差走廊，形成新的航向角约束，引导飞行器规避禁飞区。但是该类方法一次只能处理一个禁飞区，比较适用于单个或多个相距较远的禁飞区情况。此外，还有大量研究从标准轨迹着手，将带禁飞区约束的轨迹规划问题转化非线性规划问题，再基于伪谱法等直接法完成问题求解［13-16］。如文献［17］将禁飞区约束转化为不等式约束，进而通过基于网格自适应的多分辨率技术进行优化求解，但这类方法本质上还是迭代求解的思路，在面对多个复杂禁飞区约束时解算速度较慢。针对复杂约束下轨迹解算速度较慢的问题，Zhang等［18］、Li等［19］、Hu等［20］提出基于人工势场法来解决禁飞区规避制导问题，通过构建引力场、斥力场来表示目标和禁飞区的作用，并寻找综合势场中的最小负梯度方向，使得飞行器能在避开障碍的同时到达目标点。该方法具有规划求解速度快的特点，但是需要提前获取禁飞区的精确信息。文献［21］中提出一种包含了路径规划的双层轨迹规划方法，通过上层路径规划提供路径点导引信息避免轨迹陷入局部最优解，但是该方法同样需要事先获取禁飞区的准确信息。针对复杂形状的固定禁飞区轨迹规避问题，文献［22］基于模型预测控制方法，首次提出一种基于触角探测的高超声速飞行器制导方法用以进行禁飞区规避制导，该方法通过两条固定触角向两端的探测，实现了对禁飞区的规避制导，该方法的突出优势在于，不需要禁飞区的先验信息，同时还能适用于复杂形状的禁飞区。随后学者高杨在基于触角探测的制导方法上进行了更深入的探索［23-25］，文献［24］在双触角探测的基础上增加了第三条触角，用以探测飞行器正前方区域，避免了飞行器在无需机动时由于双触角探测产生的反复倾斜转弯从而造成机动能力的浪费。文献［25］中更进一步提出一种少触角和多触角的组合探测方法，先通过少触角进行粗略探测定点，再通过多触角进行精细探测，在提高了探测效率的同时还降低了计算压力。

需要指出的是，上述研究均是针对固定的禁飞区约束，禁飞区被简化为大小固定的区域，一般为禁飞圆（圆柱体或半球体），即给定禁飞区的圆心位置以及圆半径，以此构建的固定禁飞区约束是一个完全独立的再入约束，不会随着外界条件的变换而改变。通常而言，这种简化处理对于地缘政治禁飞区是合理的，但是对基于雷达探测产生的禁飞区难以适用。在实际飞行任务过程中，雷达探测距离取决于飞行器本身的雷达散射截面（RCS）［26］，而飞行器RCS 主要由本身的姿态以及其与雷达的相对位置所决定，因此基于雷达探测产生的禁飞区与飞行器状态之间存在动态耦合，对于这种动态耦合关系的建模与分析是轨迹与制导算法的精细设计的重要支撑，而目前尚未有对于动态禁飞区耦合特性建模的文献报道。因此，针对动态耦合禁飞区规避问题，本文将建立基于雷达探测产生的动态耦合禁飞区模型，提出采用触角探测反馈的制导方法进行解耦协调，通过飞行器发出的若干条触角对未来的路况信息进行预警探测，获取动态禁飞区信息，并以此为基础进行规避制导。且由于目前触角探测制导策略本质上都是固定触角探测方法，在面对动态耦合禁飞区时无法根据具体情形得到针对性触角探测策略，本文通过模糊数学和模糊逻辑将抽象的、模糊的触角探测规则具象化，从而面向复杂约束情况实时演变触角探测方法，提出基于模糊理论的自适应触角探测机动制导策略。

综上所述，考虑到由于雷达探测产生的动态禁飞区约束，本文重点研究面向动态禁飞区规避的高超声速飞行器再入机动制导问题，提出一种在不需要先验信息情况下的自适应触角探测机动制导方法。

1 高超声速滑翔飞行器再入建模

1.1 再入动力学模型

本文以无动力高超声速飞行器为研究对象，考虑地球为一均质圆球，忽略地球自转的影响，飞行器再入过程采用倾斜转弯模式，建立如下动力学方程：

式中：r为飞行器的地心距；λ为飞行器所在经度；ϕ为飞行器所在纬度；V为飞行器速度；θ为飞行器速度倾角；ψ为飞行器速度偏角；σ为飞行器倾侧角；g为重力加速度；m为飞行器质量；L为升力；D为阻力；且：

式中：CL为升力系数；CD为阻力系数；S为特征面积；ρ为大气密度。

1.2 再入约束模型

为保证再入飞行过程的顺利进行，飞行器一般需要满足特定的约束条件，主要包括热流、动压、过载约束等。其具体表达如下：

式中：k=7.97 × 10-8;，qmax，nmax分别为最大驻点热流、动压和过载。

2 动态禁飞区建模与耦合特性分析

2.1 动态禁飞区建模

面向基于雷达探测产生的动态禁飞区，其范围是雷达探测能力和飞行器RCS 耦合作用结果。由于飞行器不同入射角下的RCS 不同，因此对于任意一部雷达而言，雷达探测距离取决于雷达在飞行器体系下的视线角。而雷达视线角主要由飞行器本身地理位置和姿态决定。一方面飞行器的姿态变化会改变电磁波入射角度，另一方面，飞行器本身地理位置的改变会造成飞行器、雷达的相对位置变化。基于此，本文将对基于雷达探测产生的动态禁飞区约束进行精细化建模。

式中：

且αo为初始方位角；ϕ0为发射点纬度；λ0为发射点经度。

因此，雷达在飞行器体系下的相对位置为：

式中：

且γ为滚转角；Ψ为偏航角；φ为俯仰角。

由此可得雷达在体坐标系中的视线角：

式中：φr为雷达方向角；θr为雷达俯仰角。确定了雷达视线角后即可根据飞行器RCS 表格插值获取对应视线角的飞行器RCS值。

考虑目标单位RCS 值为σ0=1 m2，此时雷达在σ0下的标准探测距离为R0，则对任意RCS为σ(m2)的飞行器，雷达实际探测距离为：

本文的禁飞区主要指雷达扫描区域，将其表示为基于雷达有效探测半径的无限高圆柱形禁飞区，通过多个禁飞区的组合构成整体禁飞区约束模型。在禁飞区建模时，假设地球为圆球，并考虑雷达仰角、地球曲率对雷达探测半径的影响，将雷达实际探测距离Ractual转化为雷达有效探测距离Reffective。以地球表面上某一位置坐标(r0，λ0，ϕ0)作为当前飞行器位置，令第i个禁飞区的位置坐标为(ri，λi，ϕi)，其半径为Ri，由此可以将禁飞区约束表示为：

2.2 动态禁飞区耦合特性分析

由上一节的建模可知，飞行器的RCS 主要通过雷达在飞行器体坐标系中的视线角计算得到，而该视线角受多方面的影响，包括飞行器的状态、控制量、雷达位置等。为了明晰飞行器与雷达禁飞区间的耦合关系，禁飞区动态耦合特性数学描述如下：

根据坐标转换关系可得：

式中：BV=M3(α)M2(β)；VG=M1(σ)M3BG=M1(γ)M2(Ψ)M3(φ)；B，V，G分别表示飞行器体坐标系、速度坐标系和发射坐标系；分别为相对初始发射水平面的速度倾角和相对发射方向的速度偏角，其与θ，ψ可以通过射程角和初始方位角进行转换。

由此可得：

考虑倾斜转弯的飞行器，其侧滑角β始终为零，α，均为小量，所以由式（11）、（12）可得：

即：

在式（4）中α0，ϕ0，λ0，h0为已知常量，即可以表示为(λ，ϕ，r)的形式；且ϕr，λr为已知雷达坐标，即为已知常量。

所以雷达在体系下的坐标式可以表示为：

由式（15）和式（8）可知，雷达在体坐标系中的视线角可以表示为飞行器状态量(θ，ψ，λ，ϕ，r)和控制量(α，σ)的函数，即雷达视线角取决于飞行状态量和控制量。而雷达视线角又直接影响飞行器的RCS，结合式（9），飞行器RCS 的变化将导致雷达实际探测距离的改变，从而改变当前的禁飞区域。因此，基于雷达探测产生的禁飞区实质上是由飞行器状态量和控制量耦合作用的结果。

本文以某高超声速飞行器为研究对象，其在不同雷达视线角下的RCS 变化如图1 所示，其中给出了几个具体雷达俯仰角下雷达方向角从-180°到180°时飞行器RCS 的分贝数变化，分贝平方米和平方米RCS的转换如下：

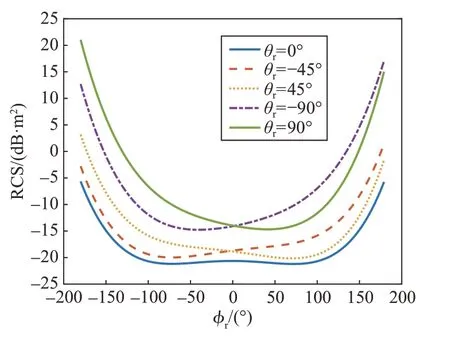
图1 不同雷达视线角下飞行器RCS变化Fig.1 The variation of RCS of an aircraft at different radar viewing angles

从中可以看出飞行器RCS 大小、正负都受雷达视线角影响较大。基于第4节的雷达部署条件和飞行器飞行条件，以雷达1探测距离为例，最大探测距离为486.26 km，最小探测距离为301.72 km，相差184.54 km，以最小探测距离作为基准，雷达的探测距离变化幅度最大超过60%，且全程波动较为剧烈。因此考虑雷达实时探测距离的改变，飞行过程中的禁飞区也是随之动态变化的。

由上述动态耦合特性分析可知，基于雷达探测产生的禁飞区约束相比于简化的固定禁飞区约束，其中存在着飞行器状态、控制的耦合项和非线性项α，σ，θ，ψ，λ，ϕ，r)。制导律决定了飞行器的各项参数变化，各参数变化又与雷达探测禁飞区密切相关，而禁飞区约束又直接影响制导律的选取，这使得飞行器本就强非线性和强耦合性的再入过程在考虑了动态耦合禁飞区约束后更为复杂。因此基于动态耦合禁飞区约束的高超声速飞行器再入机动制导方法研究具有重要意义。

3 模糊自适应触角探测制导方法

基于动态耦合禁飞区的规避制导并不是一个单纯的多可变禁飞区覆盖范围优化问题，由于禁飞区与飞行器状态量、控制量的耦合，当禁飞区的综合覆盖范围最小时，飞行器可能是指向禁飞区中心的，则此时禁飞区的覆盖范围大小并无意义。因此动态禁飞区规避制导问题的核心在于寻找一条可行路径，使得飞行器能够在复杂约束条件下规避所有动态禁飞区到达目标点。鉴于飞行器与雷达探测禁飞区之间存在的强耦合性，本文提出基于模糊理论的自适应触角探测制导策略（Fuzzy adaptive tentacle-based guidance，FATBG）来解决动态禁飞区耦合问题，通过飞行器向前方发出若干条触角并根据耦合禁飞区建模实时分析路况信息，然后结合触角反馈决定制导策略。

针对动态禁飞区的自适应规避机动制导问题，提出FATBG 方法框架，如图2 所示，主要包括动态禁飞区模块、自适应触角模块、动力学及轨迹跟踪模块3大部分。动态禁飞区模块综合飞行器状态信息以及雷达所在位置计算飞行器RCS 并建立动态禁飞区域，并将动态禁飞区实时信息传输给自适应触角模块和动力学模块；自适应触角模块包括触角生成、终止、信息综合并将探测信息结合模糊理论实时生成触角探测方案，最终制导方案传递给动力学模块；动力学模块包括飞行器动力学系统及其纵向轨迹跟踪两部分。

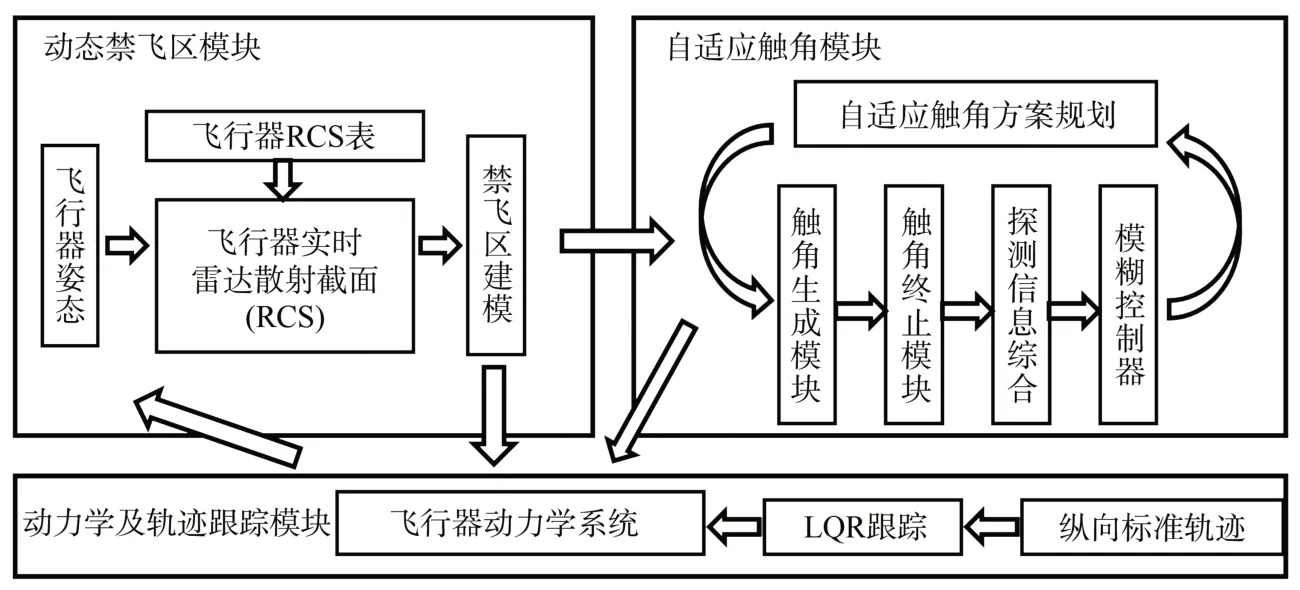
图2 FATBG方法框架Fig.2 FATBG method framework

3.1 触角模型

本文通过飞行器向前方发射出若干条触角来对飞行过程中的禁飞区进行探测，由于触角本身的探测特性，触角在延伸的过程中实时位置、姿态、控制量的改变都会对飞行器RCS 产生影响，从而在探测过程中获取雷达实际探测半径，即触角的生成过程中考虑了雷达探测范围变化的影响，通过一定数量的触角探测可以有效的获取实时雷达信息，实现对动态耦合禁飞区的规避。

每个触角产生之后都有独立的终止判定，相应终止条件如下：

C1：触角抵达任务终点，优先级为1。

C2：触角探测时间超过界限，优先级为2。

C3：触角超出方位角走廊界限，优先级为3。

C4：触角进入禁飞区域内，优先级为4。

触角终止条件的优先级代表着对于触角终止原因的可接受程度，当每条触角终止时会同时返回对应的终止条件因素。

3.2 基于模糊理论的自适应触角探测制导策略

飞行过程中由于各种因素的扰动以及实际飞行中控制量的变化，需要设计对应的标准轨迹控制律来跟踪纵向标准轨迹。本文选取线性二次型调节器（Linear Quadratic Regulator，LQR）［27］作为纵向标准轨迹的跟踪控制律：

式中：x=[ΔrΔVΔθ]T，u=Kx。

3.2.1 安全度设计

为了能够更好的适应且判断多动态耦合禁飞区的情况，本文基于飞行时间、剩余距离、触角停止原因和上一时刻触角的惯性设置了触角判断的安全度P：

式中：kCi是终止条件系数，由当前触角的终止条件决定；kSi是待飞距离系数，由触角与终点的剩余路程决定；kσi是触角惯性惩罚系数；tiFly是触角飞行时间；dσi反应了触角改变量。

安全度的设置需要考虑多方面的影响，首先就是安全飞行时间，这是决定飞行器安全性的核心；其次，还需要考虑到控制频繁大幅变造成的控制压力，所以设置飞行器的惯性参考量，作为对于飞行器控制量变化的一种阻抗，用来避免在微小改变下的控制量频繁切换；同时飞行器触角的不同终止原因对于飞行器的影响也有所不；最后考虑到不同飞行任务下各个因素的影响比重不同，需进行针对性权重分析。触角的安全度解决了面对多个触角时的选择问题，同时可以协同触角终止条件形成新的触角探测方案。

3.2.2 模糊触角规划

触角探测制导在触角探测过程中已考虑禁飞区实时动态耦合变化的影响，但是为进一步提升触角探测效率和结果，在诸如能量损失、控制量瞬变以及规避效果等方面针对不同情况设定不同的触角探测方案有望能够展现出更好的探测效果。结合飞行状况与触角探测的信息，本文提出如下模糊触角规划方法：

1) 模糊化接口

取系统的反馈量安全度和终止条件作为模糊控制器的两个输入，在P，C的论域上定义语言变量为“安全度P”、“终止条件C”；在控制量Tn的论域上定义语言变量“控制量Tn”；为便于规则实现，将P，C，Tn划分为｛“大（B）”，“中（M）”，“小（S）”｝三档。

安全度P的取值范围为［0，1 000］，超出1 000的同样记为1 000，其中B，S的隶属度函数选为广义钟型隶属函数，M的隶属度函数选为三角形；终止条件C的取值范围为Ci（i=1，2，3，4），其隶属度函数都选为高斯型隶属函数；控制律Tn取值范围为［0，9］，其中S，B的隶属度函数为梯形，M的隶属度函数选为三角形。

2) 规则库

本文采用根据过程的模糊模型生成控制规则，即通过用模糊语言描述被控过程的输入输出关系来得到过程的模糊模型，进而得到控制器的控制规则，具体推理规则如表1所示：

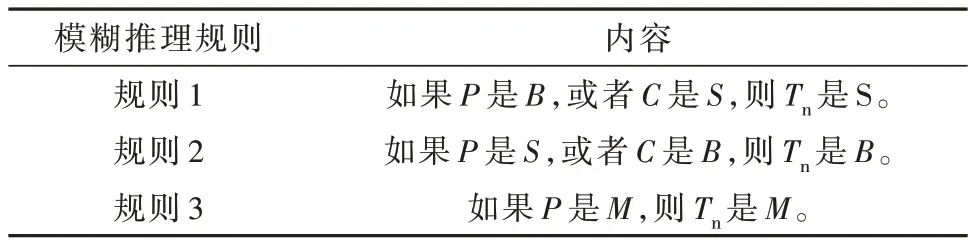
表1 模糊推理规则Table 1 Fuzzy inference rules

3) 模糊推理

根据模糊输入和推理规则库中蕴含的输入输出关系，可以得到如下的模糊控制器输出模糊值：

4) 清晰化接口

根据加权平均法（重心法）来进行反模糊化，该方法对模糊输出量中各个元素及其对应的隶属度求加权平均值，并进行四舍五入取整，来得到精确输出控制量。

式中：U*推表示输出控制量；符号表示四舍五入取整操作。

3.2.3 FATBG方法

为了明确触角的主要探测方向，基于上一时刻的触角，设计了触角比Ra，其表达式如下：

式中：b1、b2、b3、b4是待设计参数。

根据上一时刻的触角探测结果，即可计算得到对应的Tn和Ra，设上一时刻的触角倾侧角值为σ，最大倾侧角值为Mσ，以上一时刻的倾侧角为中心，下一次的触角分别向左右两侧发散。由此可以得到下一步的触角探测方案：

1) 触角探测范围：

2) 触角探测上下限：

3) 左右两侧触角分配：

式中：ceil 函数将输入舍入到大于或等于该输入的最接近整数。

4) 具体触角方案：

FATBG 通过所设计的触角反馈量实时判断飞行器可能的路况信息并形成安全度反馈信息作为下一次触角探测方案的参考之一，结合此前飞行器信息生成具体触角范围、分布安排。面对雷达探测多动态耦合禁飞区的复杂约束情况，本文所提出的自适应触角探测制导方法高效的利用了飞行器的触角反馈及此前的飞行数据，并以此为基础生成适应于当前及对未来路况信息判断的制导方法，使飞行器能够根据禁飞区的动态变化实现自适应制导。

4 数值仿真与分析

考虑一类具有较好气动外形和电磁散射特性的高超声速飞行器X-38 对所提出的FATBG 策略进行验证，飞行器总质量为2 400 kg，参考面积为0.4 m2，最大驻点热流为3 000 kW/m2，最大动压为100 kPa，最大过载为5。

飞行器初始位置为（110°，19°），终点位置为（154°，23°），初始高度为40 km，初始速度为4 800 m/s，初始速度倾角为0°，初始速度偏角为90°。禁飞区设置为4个雷达构成的探测区域，4个雷达位置分别为（120°，23°）、（135°，23°）、（128°，15°）、（140°，16°），雷达在目标单位雷达散射截面积情况下的探测距离为1 200 km，雷达存在3°仰角，同时考虑地球曲率对于雷达探测的影响，构成最终的禁飞区域。在实际仿真过程中，飞行器没有提前获取禁飞区的信息，依靠触角探测进行实时的禁飞区规避机动制导。

4.1 FATBG有效性仿真

本节根据此前所给出的飞行器数据以及禁飞区约束条件进行仿真，通过FATBG 策略获得飞行轨迹及制导指令，图3～5 为FATBG 制导策略的仿真结果，飞行全过程符合约束条件。

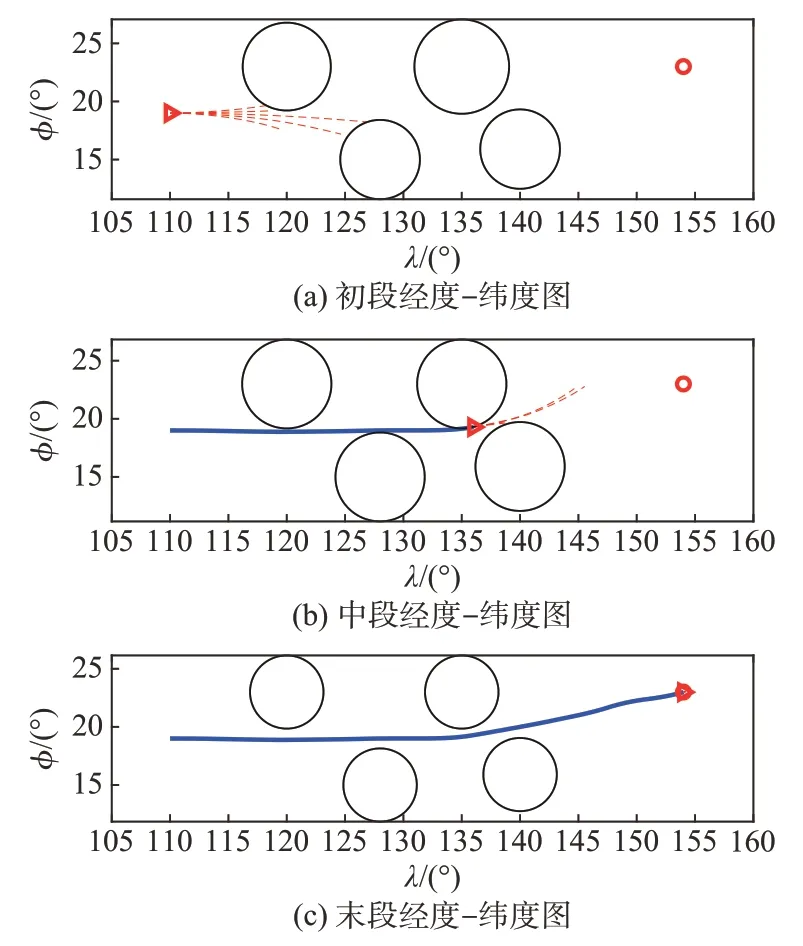
图3 全程经度-纬度图（FATBG方法）Fig.3 Longitude and latitude map（by FATBG）

图3给出了飞行器在给定四个雷达禁飞区约束条件下的平面经纬度飞行轨迹图，图中红色箭头为飞行器当前位置，红色虚线为探测触角，4 个黑色圆圈为所设置的雷达探测禁飞区，从图中可以看出4 个雷达禁飞区在不同的时间节点由于飞行器的位置、姿态的不同覆盖区域都有所变化，体现出飞行器与雷达探测禁飞区之间的耦合关系。

图4中给出了飞行器在飞行过程中的实时控制量倾侧角和攻角。从倾侧角曲线图中可以看出，基于FATBG 方法，其倾侧角的值并不是在几个固定的值上选取，而是根据触角探测的结果自适应进行调整以获取一个更适合当前飞行器位置及未来路况的制导指令。

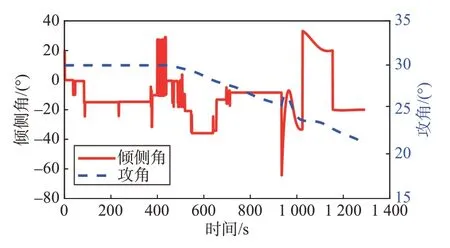
图4 控制量（FATBG方法）Fig.4 Control variables（by FATBG）

在图5的禁飞区规避情况中，4个图分别代表着1到4号雷达，图中蓝线为飞行器与各自雷达的实时距离，红色虚线代表着雷达的实时探测距离，当同一纵轴上蓝线位于红线之上时证明飞行器未进入禁飞区域。可以看出，基于本文所提出的自适应触角探测方法，飞行器实现了对雷达探测禁飞区的动态规避，同时还能顺利抵达所设置的目标点。

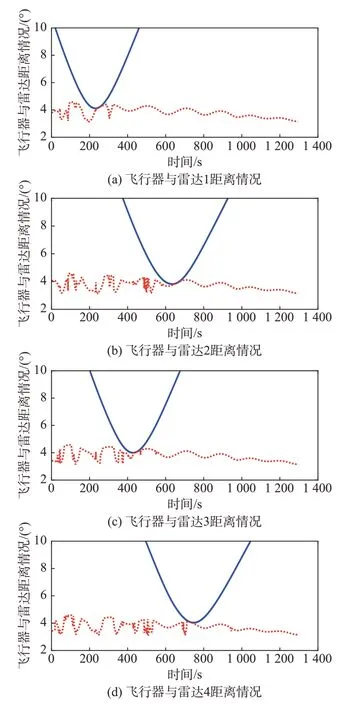
图5 禁飞区规避情况（FATBG方法）Fig.5 Avoidance of no-fly zones（by FATBG）

4.2 FATBG性能仿真分析

为了进行制导性能分析，本节将在相同的飞行条件情况下对于固定触角探测制导进行仿真试验并与FATBG 仿真相对比，图6～图8 为对比仿真结果，固定触角飞行全程满足路径约束条件。

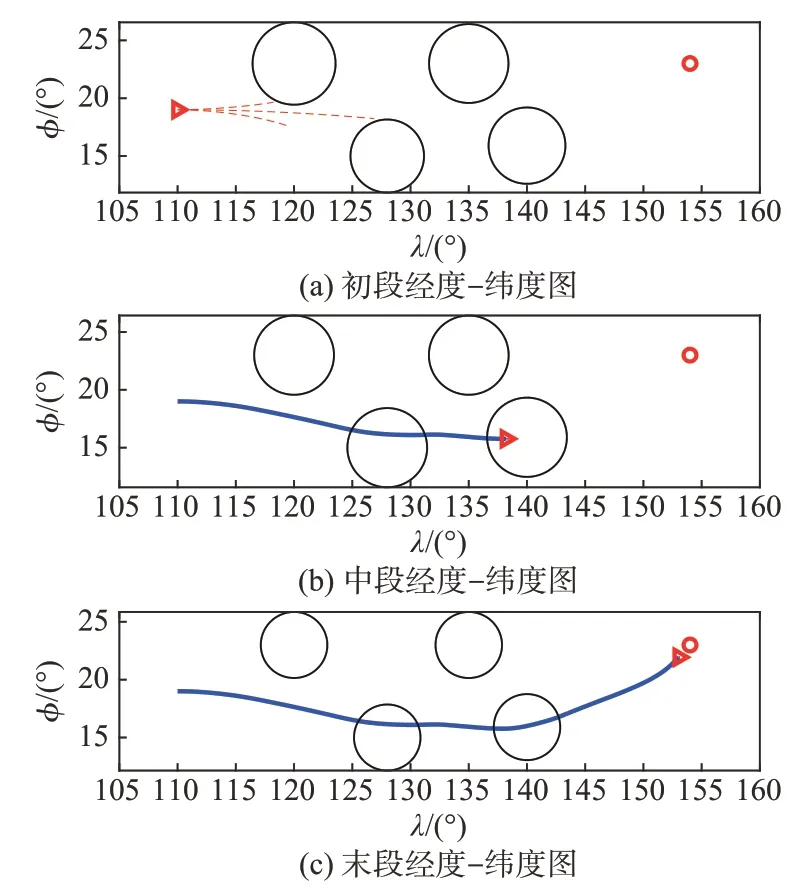
图6 全程经度-纬度图（固定触角）Fig.6 Longitude-latitude map（with fixed angles）

图6 给出了基于固定触角探测的平面经纬图，在经纬图中基于固定触角的机动制导方法下飞行器受限于飞行能力限制，最终并未能到达目标点。在相同初始条件下，一类飞行器应具有相同的飞行能力，固定触角方法对于飞行器能量的利用效率不高，而FATBG方法更能节省飞行器的能量。

图7 中给出了固定触角方法下的倾侧角控制量，从图中可以看出飞行器的倾侧角控制量始终是维持在几个固定的取值上，这使得飞行器无法针对面对的不同飞行状况做出针对性调整，只能选择固定的触角角度进行探测并反馈。同时频繁出现的大角度瞬变，加剧了飞行器控制系统的压力，也对飞行器的机动能力造成较大的浪费，最终导致飞行器由于飞行能力的不足无法抵达目标点。

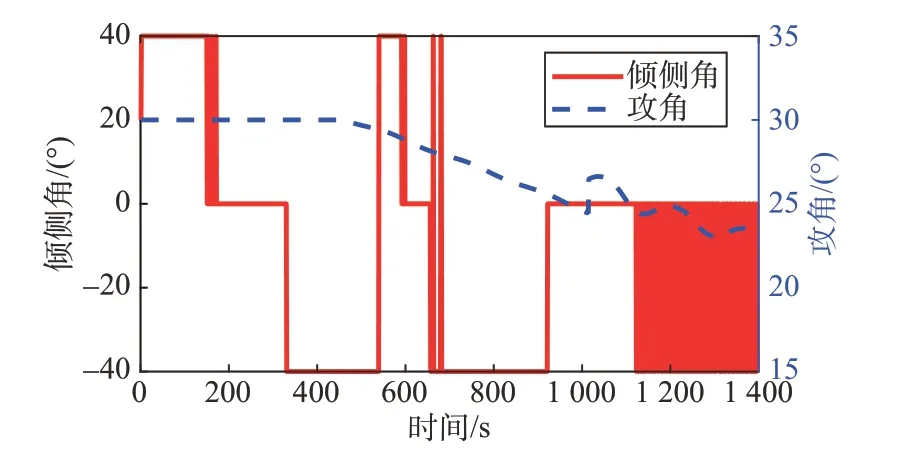
图7 控制量（固定触角）Fig.7 Control variable（with fixed angles）

图8 规避情况中可以看出，飞行器并未能够完全避开所有雷达的探测。进一步分析可知，这是由于飞行器在对1、2号禁飞区进行规避的时候产生了过度机动，比如对于2 号禁飞区始终维持了一个较大的禁飞区边缘距离，从而使得飞行器在3、4 号禁飞区时机动能力不足以进行完美规避。由于不能针对探测结果进行相应调整，使得飞行器机动能力的分配不够合理，面对复杂约束条件下的动态禁飞区机动制导，固定触角探测方法在机动能力分配和规避效果上仍然有进一步优化空间。

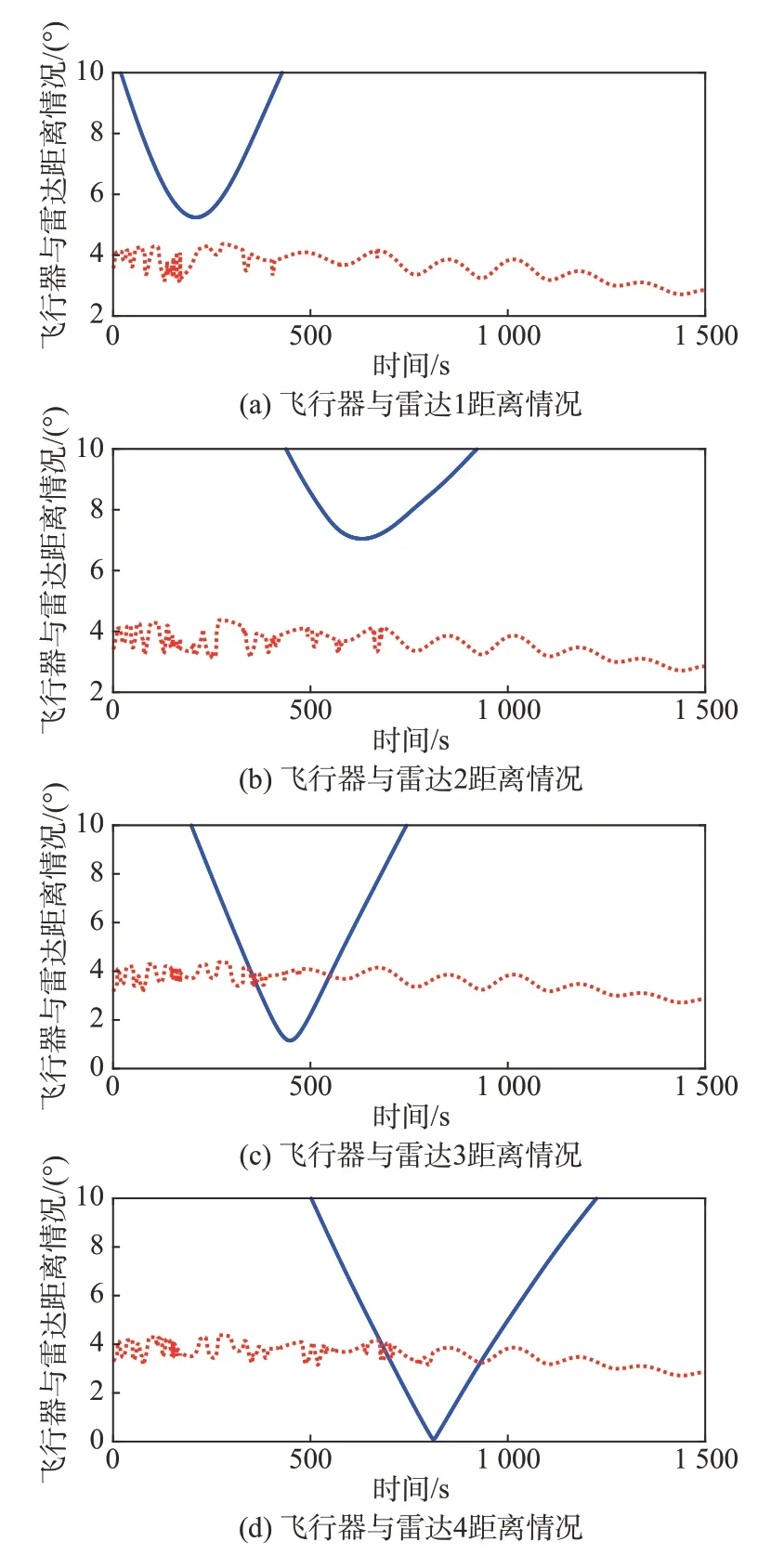
图8 规避情况（固定触角）Fig.8 Avoidance situation（with fixed angles）

通过与固定触角探测方法的仿真进行对比分析，本文所提出的FATBG 方法能够有效实现动态耦合禁飞区规避制导，对于1～4号动态禁飞区在飞行全过程中均能实现规避，而固定触角探测方法分别在3、4 号禁飞区中被探测到了191 s 和241 s。同时FATBG 方法的终端航程偏差为1.46 km，固定触角探测方法由于过度机动导致不足以飞抵目标，终端航程偏差为157.42 km。将飞行过程中倾侧角的变化幅度进行累加，可以作为衡量飞行器控制压力的指标之一，FATBG 方法为29.91，固定触角探测方法为118.68，是FATBG 的3.97 倍，这给飞行器的控制器带来了更大的压力。

最后为了检验FATBG 方法在计算时间上的实时性，在FATBG 方法仿真中记录每次模糊自适应触角规划的时间，仿真所用电脑处理器为11th Gen Intel（R）Core（TM）i7-1165G7@2.80 GHz，所用软件为MATLAB2023a，结果如图9 所示，从图中可以看出，在仿真过程中FATBG 方法的模糊规划时间均较短，平均单次规划用时5.88×10-4s，符合制导实时性要求。

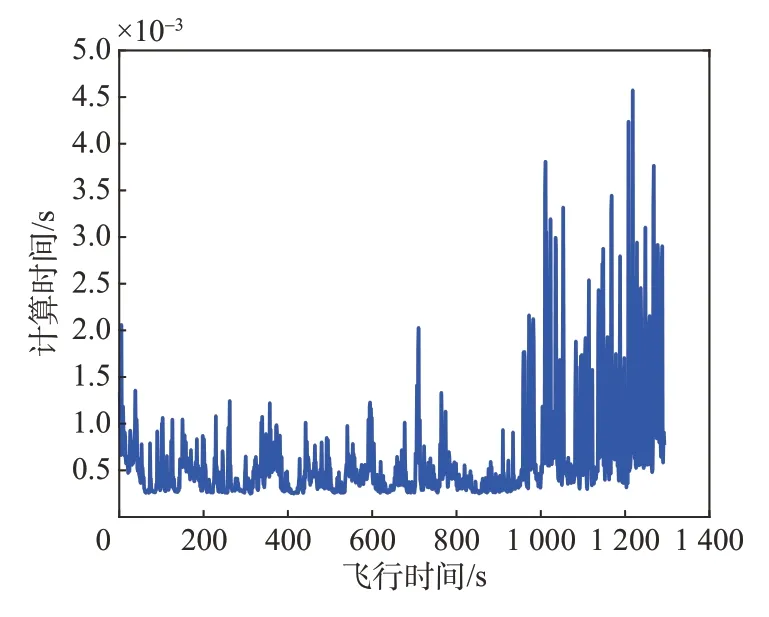
图9 FATBG-模糊触角规划时间Fig.9 FATBG-Fuzzy tentacle planning time

综上所示，FATBG 方法在飞行器机动能力分配、节省飞行能量、动态耦合禁飞区规避效果、降低飞行器控制压力等几个方面都有着更良好的表现。

5 结论

针对面向雷达探测产生的动态耦合禁飞区再入机动制导问题，本文提出一种基于模糊理论的自适应触角探测机动制导方法。首先建立动态耦合禁飞区，并利用触角探测未知的路况信息，以此实现对动态禁飞区的规避绕飞。然后提出自适应触角探测制导策略，根据反馈结果构建针对性触角探测方案。最后仿真结果表明所提方法能够实现动态禁飞区规避绕飞，并在节省飞行能量、提高机动能力、降低控制压力等方面均有良好表现。