采用利希滕贝格图的高超声速飞行器轨迹优化
张笑妍,程昊宇,韩博,闫杰
(1.西北工业大学无人系统技术研究院,西安 710072;2.中国人民解放军93525部队,日喀则 857000)
0 引言
高超声速飞行器(Hypersonic flight vehicle,HFV)由于具备快速的全球打击能力和灵活的机动性等特点,受到研究人员的广泛关注[1-2]。HFV一般在距地表约100~120 km 的高度进入大气层,整个弹道通常在约20~30 km 的高度扩散到终端区域[3]。再入轨迹的优化在HFV 性能中起着重要作用,其产生的控制指令能够引导飞行器从初始状态飞向特定的终端状态,确保HFV 能够精确和快速地到达目标点[4]。
HFV 再入段有大包线、多约束飞行等特点,使得再入参考轨迹的设计优化尤其具有挑战性。HFV除了会在复杂环境中受到大量约束,如终端条件约束、状态边界约束、热流速率约束、动压约束以及法向过载约束等[5],其再入轨迹优化还需要根据任务要求满足终端时间最短、能量最小或终端速度误差最小等性能指标。因此,再入轨迹优化实际上是一个多约束优化问题[6]。在现有文献中,求解高超声速飞行器再入轨迹优化问题的方法一般可分为2 大类:数值方法和启发式优化算法。近年,学者通过数值法中的直接方法对作为最优控制问题的HFV 的再入轨迹优化进行了大量研究[7]。直接方法,特别是伪谱法,可以将高超声速飞行器轨迹优化问题转化为非线性规划(Nonlinear programming problem,NLP)问题,直接通过传统方法解决,而不需要推导出一阶必要条件。相较于其他直接方法,伪谱法求解速度快且求解精度高,被广泛应用于复杂多约束优化问题的求解中。Patterson 提出了高斯伪谱法(Gauss pseudospectral method,GPM),用于解决多阶段最优控制问题[8]。利用GPM 解决HFV 再入段轨迹优化问题,可以快速获得满足约束条件的轨迹。但实际解决HFV 再入段轨迹优化问题时,约束条件多、优化问题的复杂性强,由于GPM 全局搜索能力差,其性能对初始估计值的依赖性会增强[9]。初始值选择不当会造成算法陷入局部最优,甚至发散,这一缺点使得调参难度大,轨迹优化结果受设计者经验影响。
针对以上问题,广大学者利用启发式智能优化算法简单、灵活、全局搜索能力强等优点,开展轨迹优化算法研究,以克服GPM 算法过于依赖初始值、全局搜索能力不足的缺点。对于复杂优化问题,启发式算法在全局搜索方面具有显著优势,但在全局最优附近的收敛速度和收敛精度相对于数值方法较差[10-11]。为了充分发挥数值方法和启发式优化算法各自的优点,大量学者对混合算法进行了研究。文献[12]将鲸鱼优化算法和高斯伪谱法相结合,为伪谱法提供更好的初值。文献[13]改进了麻雀优化算法并结合控制变量参数化方法设计混合算法,应用于高超声速飞行器的轨迹优化。上述方法在处理约束时均将约束转化为惩罚函数的形式,参数复杂、对研究人员的经验依赖性强,且上层中算法为GPM 提供的初始解效能较差,使混合算法收敛精度不足,鲁棒性不强。
基于扩散限制聚集理论,可将利希滕贝格图(Lichtenberg figure,LF)[14]应用于利希滕贝格算法(Lichtenberg algorithm,LA)中。与许多文献中的算法不同,LA 是一种成功地利用了分形的混合算法,它由基于群体和轨迹的搜索方法组成,这种组成模式能够提高迭代过程的稳定性,在探索和利用之间产生良好的平衡,具有更高的收敛精度和鲁棒性。该算法在复杂多约束优化问题中具有优越的求解性能[15],适合应用在高超声速飞行器再入轨迹优化问题中。
为提升高超声速飞行器再入轨迹优化问题的求解效率和精度,本文首先提出了一种自适应分段利希滕贝格算法(Adaptive piecewise Lichtenberg algorithm,APLA),其在解决带约束的优化问题方面具有明显优势。算法针对所解决问题的特点,基于拉丁超立方抽样(Latin hypercube sampling,LHS)[16]改进了初始化方法,最大化提高算法前期收敛速度和全局搜索能力。在迭代阶段采用了全局至局部的自适应分层策略分阶段维护多样性,提升搜索精度。提出的策略使APLA 在保证收敛速度的前提下提升算法的全局搜索能力。接着,将APLA 和GPM结合提出再入轨迹优化混合算法即APLA_GPM 算法,有效减少了参数的数目,降低了参数的调节难度,提高了算法的收敛速度、求解精度以及鲁棒性。首先,利用GPM 算法将轨迹优化问题转化为NLP 问题,继而利用具备较好全局搜索能力的APLA 算法作为初始化搜索器,求出再入过程的近似最优解序列。最后,将前一搜索阶段中,APLA 获得的近似最优解作为GPM 中NLP 求解器的初始解。利用GPM优越的收敛速度和更高的搜索精度,在近似最优解附近寻找精确的最优解。
1 高超声速飞行器再入轨迹优化问题建模
1.1 高超声速飞行器动力学与约束
考虑高超声速飞行器再入段动力学模型:
式 中:状态量x=[r,ϕ,θ,v,γ,ψ]T;控制量u=[α,σ]T;t表示时间;m是飞行器的质量;g为引力常量;r为地心距离;γ为航迹倾角;v为速率;ϕ为经度;θ为纬度;ψ为方位角;α为攻角;σ为倾侧角;D和L分别是气动阻力和升力大小,可以表示为:
式中:ρ为大气密度;ρ0为海平面空气密度;Re代表地球半径;hd是大气密度标高;CD和CL分别为阻力系数和升力系数;M是马赫数;S是HFV的参考面积。
式中:kQ是一个常数,与HFV的结构特性相关。
在建立HFV 模型的基础上,选取攻角α及倾侧角σ作为控制量即u=[α,σ]T,需要满足控制约束(式(5))。状态量x=[r,ϕ,θ,v,γ,ψ]T需满足边界约束、初值约束和终端约束(式(6)):
式中:“≤”表示每个对应元素都满足“≤”关系;Umin=[αmin,σmin]T和Umax=[αmax,σmax]T分别代表控制量的下边界和上边界;x0=[r0,ϕ0,θ0,v0,γ0,ψ0]T为状态量的初值;xf=[rf,ϕf,θf,vf,γf,ψf]T为状态的终值;Xmin和Xmax分别为状态的下边界和上边界;t0和tf分别表示初始时间和终端时间。
1.2 高超声速飞行器再入任务代价函数
考虑如下高超声速飞行器再入段轨迹优化问题,将最大化纵程轨迹及轨迹平滑作为任务,则可将问题转化为如下所示的NLP问题:
式中:τ为权重因子;Gmax=[,Pmax,Nmax]T为约束量的上边界矩阵;Gmin=[,Pmin,Nmin]T为约束量的下边界矩阵;g(x)=[,Pd(x),nL(x)]T。
2 自适应分段利希滕贝格算法
2.1 利希滕贝格算法
LF 以矩阵F的形式表示。在LA 中构建LF 需要3个重要的参数,粒子数量Np、粘性系数Sp和创建半径Rc。其中Rc决定矩阵的行列。粒子在整个矩阵中随机释放,将其行走随机地、径向地绘制出来。集群中的每个粒子都可以转化为笛卡尔平面上的位置,并将位置四舍五入为一个具有行号和列号的矩阵元素。Sp对图的密度有很大影响,Sp越小,粒子粘在某个集群上的概率越小,集群的密度就会增加。
LA用有限数量的点来映射搜索空间,以便在目标函数中进行评估。其中,前一次迭代的最佳点Pb总是当前迭代的触发点Xs,但它不一定是要再次评估的点。在第一次迭代中,它是随机选择的LF点中的一个。每次迭代时在整个LF 中选择代表群体的LF 特征点,称为利希滕贝格点(Lichtenberg point,LP),并保证这些LP 一定在规定的搜索空间内。这种形式使LA 兼备群体和轨迹2种搜索方式,成为一种混合算法。LP的生成公式如下所示:
2.2 改进利希滕贝格算法
LA算法存在两方面缺点,一方面是算法初始化阶段粒子在空间内分布不均匀,导致全局搜索能力差且收敛速度慢。另一方面是迭代搜索过程中,算法前期全局搜索能力强但收敛速率慢,后期粒子多样性差,全局搜索性能降低。针对LA 算法的不足,及高超声速飞行器再入轨迹优化问题多约束、强耦合的特点对LA 算法进行了改进,提出了APLA 算法。通过优化初始解的效能加速算法前期的收敛速度并提高前期全局搜索能力。高超声速飞行器再入轨迹优化问题约束多且复杂性较高,算法易陷入局部最优,使求解精度降低。本文提出了全局-局部交叉自适应更新方法,在保证算法全局搜索性能的前提下,提高算法收敛速度。
图1 是APLA 算法的流程。其中,行向量LjP为矩阵LP的第j行;Pb(i)为第i次迭代中的最优位置。
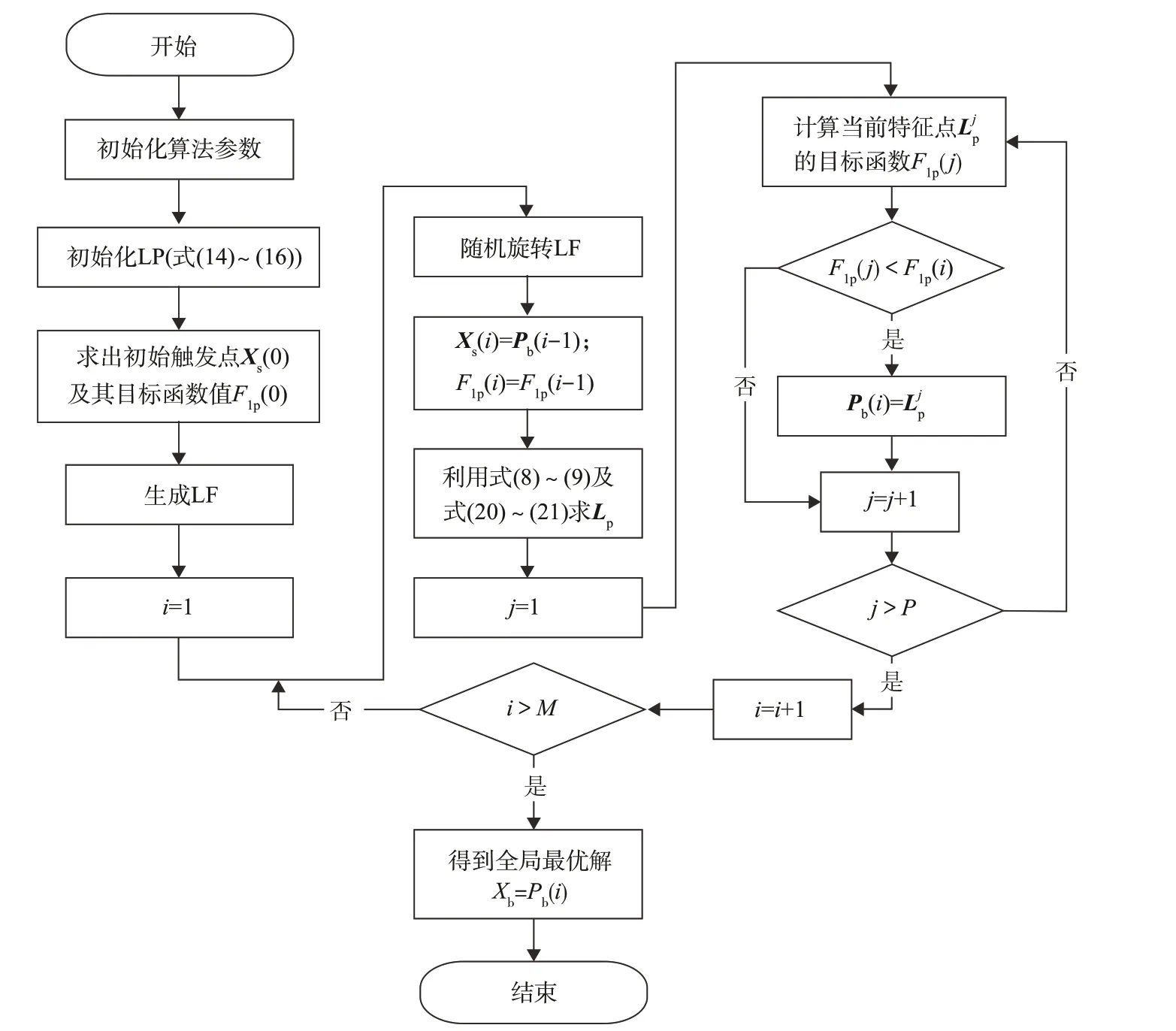
图1 APLA流程图Fig.1 APLA flowchart
2.2.1 拉丁超立方抽样初始化
初始触发点需要在算法迭代前选出,它的质量影响着APLA 后续迭代的效率。良好的初始触发点能够加速算法收敛,提升算法前期解的质量。本文通过引入LHS 改进粒子位置初始化,如式(14)~(16)所示,提升触发点备选解在搜索空间中分布的均匀性,从而提升初始触发点的全局优越性。LHS是一种分层抽样技术,它使用多变量参数分布的近似随机抽样方法来创建初始位置,适用于本文研究的高超声速飞行器再入轨迹优化问题。
2.2.2 全局——局部交叉自适应更新
在保证算法全局搜索效率的同时,为了加快算法的收敛速度,设计自适应参数,收缩率ξ∈[0,1],用以加速局部搜索。通过ξ创建副图,其与主图具有相同的触发点,使算法能够在一个较小的局部区间内快速搜索寻优,从而加速算法的收敛。为了在提高收敛速率的基础上防止算法早熟,在迭代在前期ξ是一个较大的值,后期粒子分布较集中,收缩率将随着迭代的进行不断减小,增加主图所占比例。ξ的更新公式如下所示:
式中:M表示算法最大迭代次数;i表示当前迭代数;Δ ∈(0,0.2)是正常数,根据实际问题设置。
在算法迭代的过程中,用于计算目标函数的粒子由取自主图的粒子(LPG)和取自副图的粒子(LPL)组成。LPG 主要用于提升粒子多样性,防止算法陷入局部最优。LPL用于在当前最优点附近搜索,加速算法收敛。前期多样性较为丰富且ξ较大,LPL 应占主导地位。后期粒子多样性减少,应增加LPG 所占比例。综上,需要对2 类粒子的数量进行设计:
式中:Pg为从主图选取的粒子数;i表示当前迭代数;τ∈[1,1.7]是正常数,根据实际问题设置。
综上,经过改进的粒子更新公式如下所示:
图2为APLA迭代中粒子分布示意图,x1,x2为粒子在分布空间中的坐标分量。对比图2(a)与图2(b)可知:算法前期局部LF 占比大,LP 在空间中分布均匀,算法全局搜索能力强;后期局部LF 占比逐渐缩小,增强算法局部搜索能力并加快收敛,LP 分布在全局LF 中的比例增加,保证种群多样性,防止算法陷入局部最优。
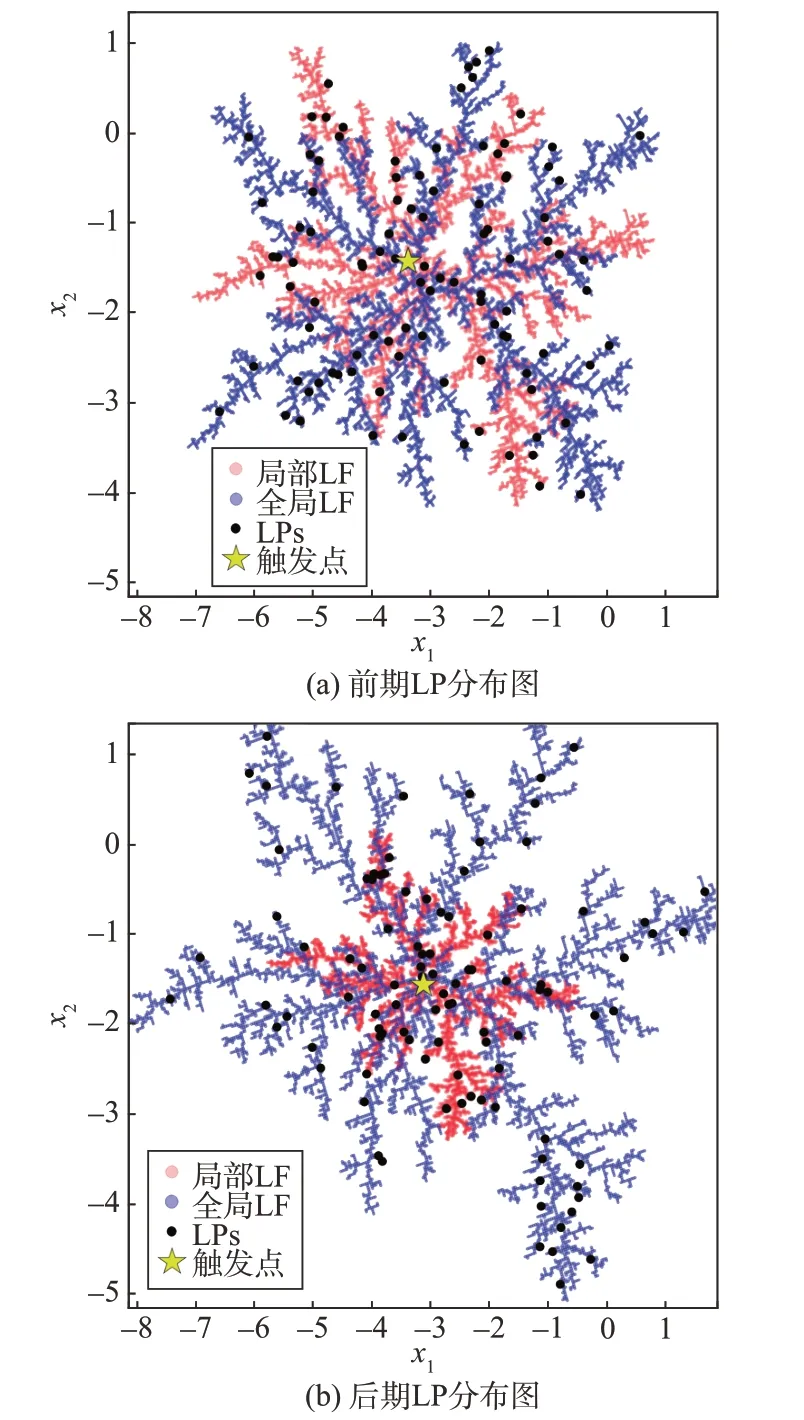
图2 利希滕贝格图中的LP分布Fig.2 LP distribution in the Lichtenberg figures
3 APLA_GPM 高超声速飞行器再入轨迹优化方法
3.1 高斯伪谱法
本文通过GPM[17]将时间区间为[t0,tf]的高超声速飞行器再入轨迹优化问题(式(1)~(7))转化为NLP 问题进行求解,首先需要将其时间区间转化到GPM的时间区间[-1,1]上:
进而,微分状态为:
式中:D∈R(N-1)×N为微分矩阵,k=1,2,…,N-1。
将原问题的动力学微分约束转换为在配点上完全等价的代数约束:
利用高斯积分近似离散化的终端状态及代价函数得到:
另外,终端约束条件及路径约束条件分别表示为式(28)~(29):
综上,GPM 将高超声速飞行器再入轨迹优化问题转化为如式(26)~(29)所示的NLP问题。
3.2 APLA约束处理
经典LA 算法最初提出的目的即求解多约束优化问题,因此它是求解具有线性和非线性约束实际问题的强大工具。APLA 在经典LA 对约束的处理方法的基础上,根据高超声速飞行器再入轨迹优化问题的特点优化处理参数,提升算法针对本问题的求解效能。转化后高超声速飞行器再入轨迹优化的目标函数为:
式中:k为不等式约束的总数;Hi(x)表示第i个不等式的被约束量的值;Bi为当前约束的边界值;λ=10为惩罚因子;εi为惩罚标记,当不满足当前约束时εi=1,满足约束则εi=0。
3.3 APLA_GPM优化方法
本文将高超声速飞行器再入轨迹优化问题转化为NLP 问题。GPM 由于具备求解精度高和搜索速度快等卓越性能,被广泛用于求解NLP 问题。但其对初始值的依赖性强,调试难度大,容易陷入局部最优甚至发散无法求解。针对这一缺点,提出APLA_GPM,利用APLA 算法强大的全局搜索能力及优秀的收敛速度为GPM 提供良好的初始解,而GPM 则弥补了APLA 在最优解附近求解精度较低的缺点。将两种算法的优点结合,极大地增强了问题的求解效率。图3 为APLA_GPM 轨迹优化算法框架,详细过程如下:
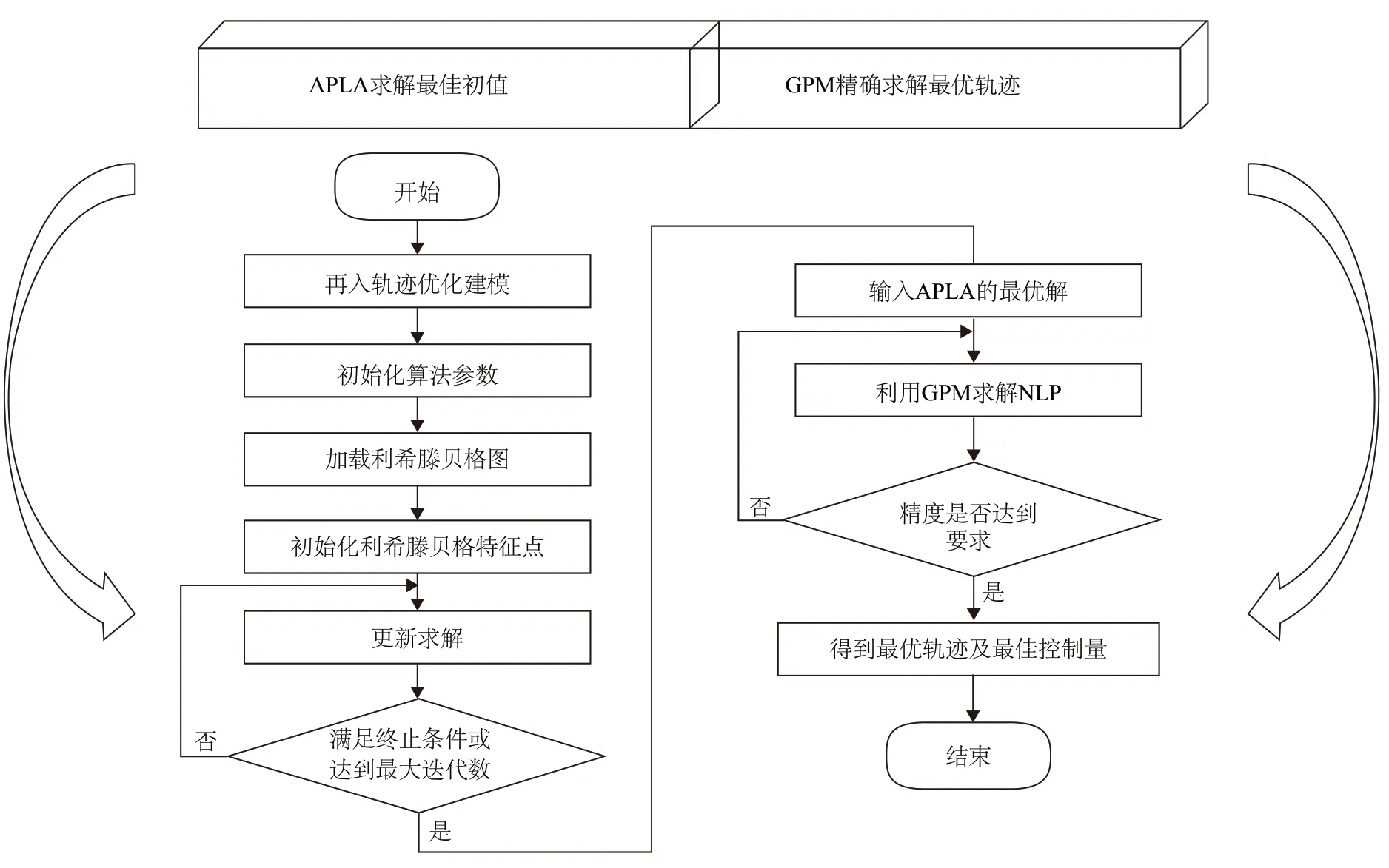
图3 轨迹优化算法框架Fig.3 Framework of trajectory optimization algorithm
1) 高超声速飞行器再入轨迹优化问题建模(式(1)~(7));
2) 设置APLA 所需的参数,包括Np、Sp、Rc、p、M以及优化误差eA;
3) 初始化LPs求出初始触发点,并生成LF;
4) 执行APLA 更新LPs 得到当前时刻下的最佳控制量;
5) 保存当前状态量及控制量并判断当前状态是否满足‖x(t) -xf‖2 6) 以APLA 获取的最优解序列作为GPM 的初始解; 7) 利用GPM 的NLP 求解器在初始解附近搜索最佳解,若NLP求解精度达到eG,终止GPM; 8) 输出最优状态量及控制量,完成高超声速飞行器再入轨迹优化。 利用5 个带约束基准优化问题(G3 函数(F1)、Martin 和Gaddy 函数(F2)、用立方体和直线约束的Rosenbrock 函 数(F3)、Bird 函 数(F4)、G2 函 数(F5))[18]以及焊接梁问题(F6)[19]进行数值测试,将APLA 的性能与WOA[20]、SSA[21]、PSO[22]以及LA 的性能进行对比分析,以验证本研究提出算法优越的全局搜索能力与收敛精度。APLA中τ越大,Pg的初始值和最大值越大,Pg变化越平缓,Pg的变化范围越小,本文中τ=1.3,M=100,p=10d。图4 为各算法应用于相应测试函数的收敛曲线。表1为将上述算法应用于各个测试函数并进行蒙特卡洛仿真的结果,其中最优解、平均最优解和标准差为各算法独立运行1 500次得出的解所求。 表1 算法应用于各测试函数中的结果Table 1 Results of the algorithm applied to each test function 图4 算法在各测试函数上的收敛曲线对比Fig.4 Comparison of convergence curves of algorithms on various test functions 如图4 所示,对比5 种算法在各带约束问题中的收敛曲线,可以得出:APLA 具有良好的初始解,加速了算法的收敛过程。采用全局-局部交叉自适应更新策略,使得APLA 不仅以更小的迭代次数收敛至最优解,且全局搜索性能明显强于WOA、SSA、PSO以及LA。 进一步,通过分析表1中的数据可以看出,本文所提算法在测试实例中的最优解和平均最优解均优于其他算法,且标准差很小。这一结果证明了APLA 鲁棒性强且收敛精度高,适合解决带约束的优化问题。 本节通过将APLA_GPM与传统GPM、WOAGPM、SSAGPM 以及LAGPM 进行对比,验证本文所提方法在解决高超声速飞行器再入轨迹优化问题上的优越性。 在当前高超声速飞行器再入轨迹优化问题中,算法参数设置为τ=1.3,Δ=0.06,M=100,p=100。控制量的上限和下限分别设置为Umin=[10,-70]T,Umax=[20,70]T。路径约束中Qmax=3 000 kW/m2,Pmax=75 kPa,Nmax=2.5 g。高超声速飞行器再入轨迹参数设置见表2,飞行器初始条件与终端条件如表3所示。 表2 高超声速飞行器再入轨迹参数Table 2 Re-entry trajectory parameters of hypersonic vehicle 表3 飞行器初始和终端条件设置Table 3 Initial and terminal condition setting of vehicle 图5给出了高超声速飞行器初始化过程中的收敛曲线。可以看出,APLA 可以用更少的迭代次数获得更小的适应度值。这一结果表明相对于其他算法,APLA 可以用更少的时间完成上层中的初始化搜索阶段,并切换到下层,为APLA_GPM 提供了寻找全局最优解的最佳初始解集。 图5 再入轨迹优化初始化收敛曲线Fig.5 Convergence curves of initialization for the re-entry trajectory optimization 图6为各算法求解高超声速飞行器再入轨迹优化问题的对比仿真结果。可以看出,GPM、WOAGPM、SSAGPM、LAGPM 以及APLA_GPM 5 种算法所求得的解均满足高度、速度、航迹倾角和方位角终端约束。 图6 再入轨迹优化结果对比Fig.6 Re-entry trajectory optimization results comparison 进一步由图6(b)可知,GPM 算法优化得到的纵程轨迹最短,而由APLA_GPM 算法求解得到的纵程轨迹最长,LAGPM 次之。证明APLA_GPM 在最大化纵程轨迹任务中表现优越。观察图6(d)可得,由APLA_GPM 算法求解的航迹倾角随时间的变化曲线波动最小,最为平滑,而由WOAGPM 和SSAGPM等算法求解的航迹倾角随时间的变化曲线波动剧烈,观察地心距离、速度以及方位角随时间的变化曲线得到的结论相同。 通过以上分析可以得出如下结论:相同条件下,由APLA_GPM 求得的解,在平滑度、精度上都优于GPM、WOAGPM、SSAGPM 以 及LAGPM 所 得的解。 为进一步验证本文提出算法的优越性,对GPM、WOAGPM、SSAGPM、LAGPM 以及APLA_GPM进行了蒙特卡罗仿真。每个算法独立运行1 000次。为了表征各算法所求解的平滑度、精度以及算法的求解速度,统计各算法所得高度、速度、航迹倾角以及方位角随时间变化函数的导数(r′,v′,γ′和ψ′)的标准差平均值、终端经度平均值、目标函数的平均值和最优值以及算法平均运行时间,统计数据如表4所示。 表4 蒙特卡洛仿真数据统计Table 4 Monte Carlo simulation data statistics 分析数据,可知APLA_GPM 所解得的高度、速度、航迹倾角以及方位角函数导数的标准差均小于其他方法,证明其所得轨迹更加平滑。从各个算法所求得的终端经度平均值可得出,本研究提出的算法纵程轨迹最大化能力优于其他算法。最后,APLA_GPM 目标函数的平均值最小且平均运行时间最短,证明其不仅在优化精确性和鲁棒性方面的表现明显优于GPM、WOAGPM、SSAGPM、LAGPM,且在收敛速度方面也优于其他算法。 综上,通过仿真分析得出,APLA_GPM 算法用于解决本文中提出的高超声速飞行器再入轨迹优化问题具有优越性。 针对具有复杂约束的高超声速飞行器再入轨迹优化问题,本文提出了APLA_GPM 混合方法。该方法利用APLA 快速生成最佳初始解,结合GPM 强大的局部搜索能力和优越的收敛速度在初始解周围搜索最优解。数值仿真分析结果表明,APLA 算法不仅收敛速度快且具有优越的全局搜索性能,弥补了传统伪谱法对初值的依赖性强以及全局搜索性能差的缺点。高超声速飞行器再入轨迹优化仿真结果表明,APLA_GPM 以更高的搜索精度、更快的搜索速度完成优化指标且鲁棒性优于其他算法,解得的轨迹更平滑且纵程轨迹更长。4 仿真校验
4.1 APLA数值测试分析
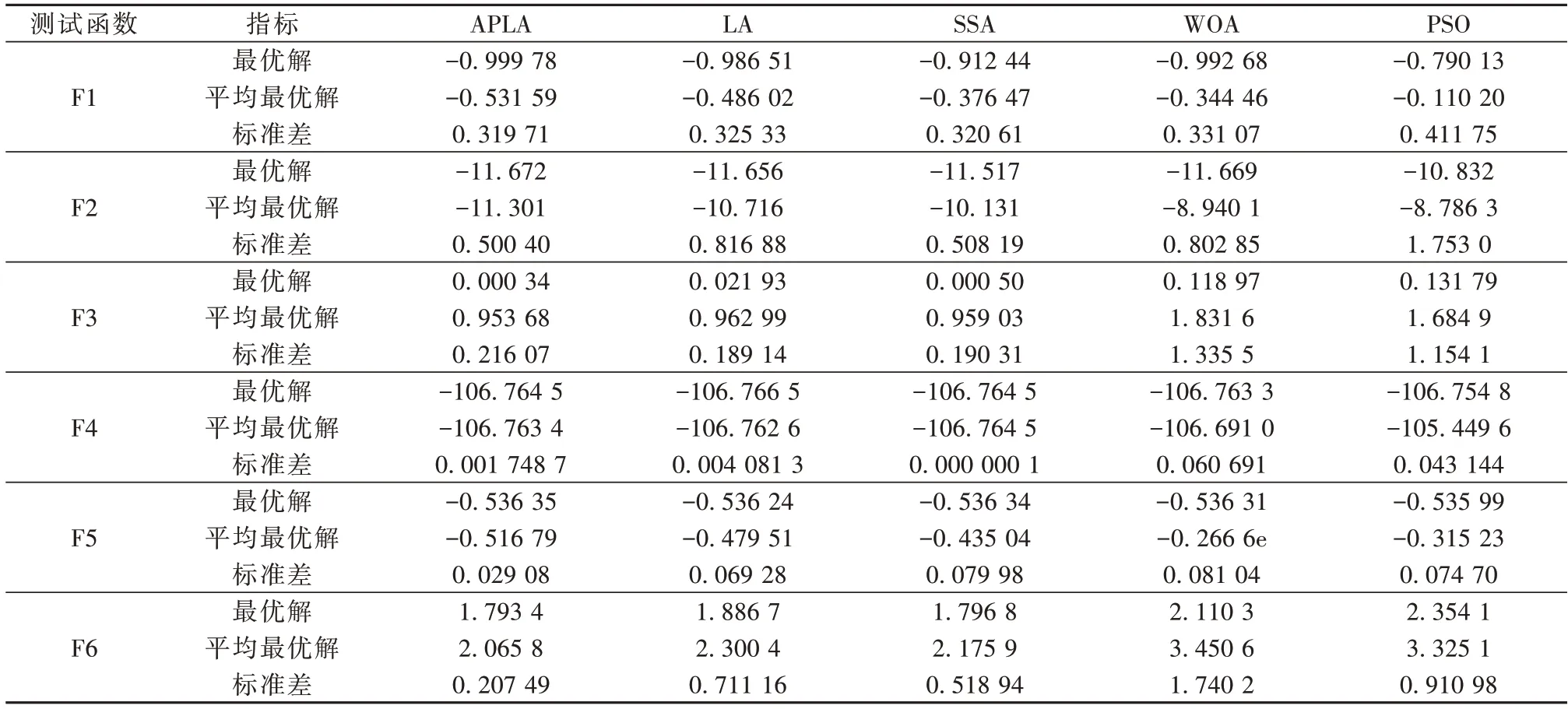
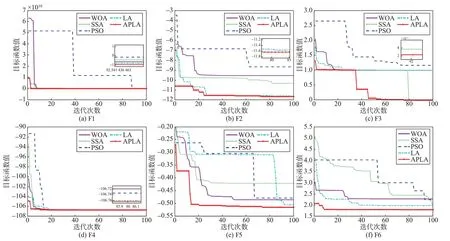
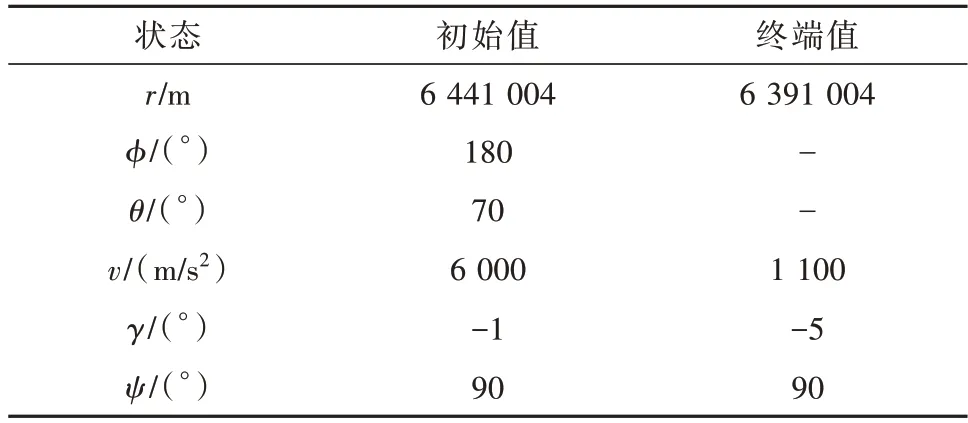
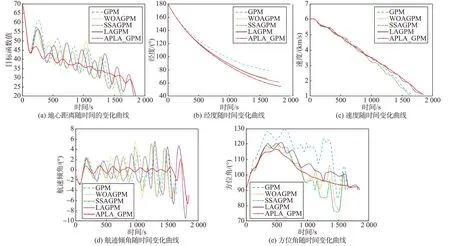
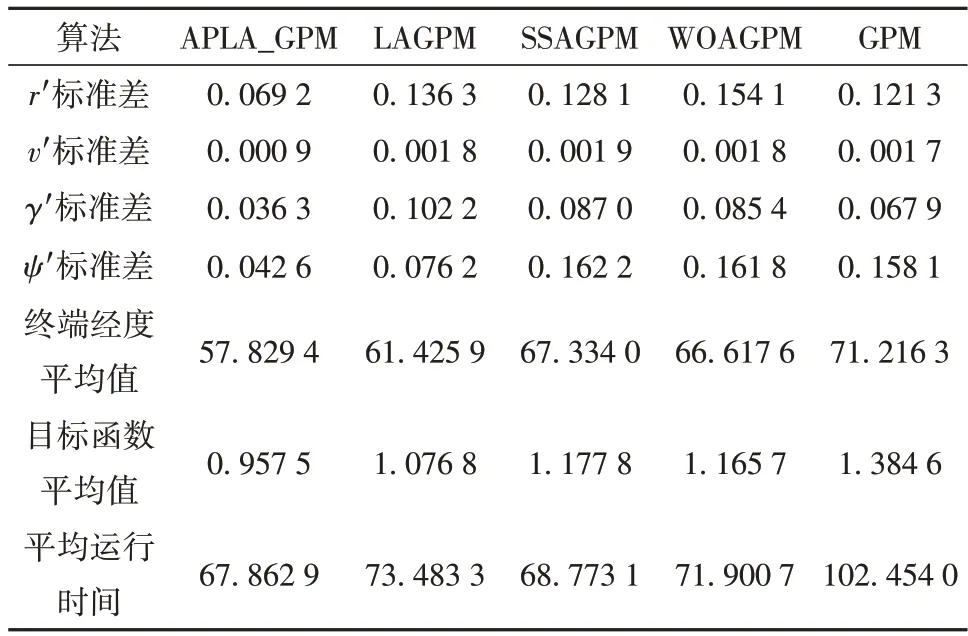
4.2 APLA_GPM仿真分析


5 结论

