面向高超声速滑翔目标的多模型多意图融合轨迹预测

李佳丽，郭杰，唐胜景

（1.北京理工大学宇航学院，北京 100081；2.飞行器动力学与控制教育部重点实验室（北京理工大学），北京 100081）

0 引言

高超声速滑翔飞行器指飞行马赫数超过5的飞行器，主要在距离海平面20～100 km 的临近空间飞行。它具有飞行速度快、作战范围广、机动能力强等特点，因而与传统目标相比，其轨迹可预测性大大降低，轨迹预测难度显著增加［1-2］。根据目标潜在信息挖掘利用方式的不同，可将轨迹预测方法分为基于统计分析的轨迹预测、基于运动机理的轨迹预测与基于意图推断的轨迹预测3类。

基于统计分析的轨迹预测方法通过目标历史信息分析，获取飞行轨迹的统计学特征，并据此预测未来轨迹。韩春耀等［1］将轨迹序列分解为趋势项、周期项与随机项，通过加法或乘法模型集成获取预测轨迹。Li等［2］通过Hough变换将目标横向、纵向轨迹分别描述为二次函数与复合函数（线性项+周期项）进行预测。张博伦等［3］将侧向加速度拟合为三次函数，假定其他方向加速度为常值，通过数值积分解算预测轨迹。随着机器学习技术的发展，部分学者将神经网络应用于轨迹预测领域。Xie等［4］将轨迹预测考虑为多元时间序列预测问题，构造包含非线性模式与线性模式的双通道双向神经网络挖掘轨迹规律。类似地，杨春伟等［5］利用长短期记忆网络解决序列预测问题，基于注意力机制构建序列到序列预测模型。Sun等［6］在无跟踪误差的假设下推导了预测模型，并利用长短期记忆网络估计参数范围，实现飞行管道预测。

基于运动机理的轨迹预测方法通过挖掘和利用目标的运动机理信息解算预测轨迹。李世杰等［7］将控制变量拟合为多项式和三角函数的复合函数，将其代入动力学模型积分得到预测轨迹。Moon等［8］采用多模型交互算法估计目标状态，通过正则化线性回归、支持向量回归和高斯过程回归等方法实现弹道系数预测。Li等［9］利用经验模态分解方法对气动加速度的多个子项进行分解与聚合，通过先验基函数对聚类数据进行拟合实现轨迹预测。程云鹏等［10］对高超声速滑翔飞行器的纵向、侧向典型机动模式进行标定，利用支持向量机进行模式识别从而实现轨迹预测。张君彪等［11］与李明杰等［12-13］利用长短期记忆神经网络对再入滑翔目标控制参数进行预测与重构，代入动力学模型解算预测轨迹。Zhang等［14］通过经验小波变换与灰色关联度对控制参数进行去噪处理，利用注意力卷积长短期记忆网络进行轨迹预测。

基于统计分析与基于运动机理的预测方法均依赖目标历史信息，一旦目标在预测过程中发生机动，预测精度便会大大降低，且预测窗口非常有限，无法满足高超声速滑翔目标防御作战需求。基于意图推断的轨迹预测方法通过挖掘攻防博弈过程中的目标意图信息，能够提高目标运动趋势预测的可靠度，提高长时轨迹预测精度，被视为高超声速滑翔目标轨迹预测的有效手段。张凯等［15］对传统轨迹预测方法与高超声速滑翔飞行器特点进行了分析，从预测模型、预测误差、制导规律和意图信息4 个角度探讨了长时轨迹预测关键技术，并阐述了目标状态与其意图推断相结合的轨迹预测思路。基于此思路，王开园等［16］在确定攻击某意图的前提下，通过离散化设计H-V 剖面二次项系数、升阻比与终端需求速度构建机动模型集，利用跟踪阶段获取的模型概率生成预测轨迹簇。张凯等［17］通过意图代价函数与贝叶斯理论推断机动模式，利用蒙特卡洛采样近似飞行器状态后验概率分布实现轨迹预测。Hu等［18］假设高度与弹道倾角为常值简化动力学模型，快速解算可达区并离散化，基于贝叶斯理论与蒙特卡洛采样实现轨迹预测，但是该文献将参数概率转化为区域概率估计问题，未考虑状态转移的动力学约束。

目前基于意图推断的轨迹预测方法研究成果较少，且已有方法中，多采用蒙特卡洛方法，导致预测模型误差大，计算复杂。为进一步提高强机动目标轨迹预测精度，满足长时轨迹预测需求，本文提出了一种基于贝叶斯理论的多模型多意图融合轨迹预测方法。首先，根据典型控制规律分析，以升力参数、阻力参数、倾侧角幅值与倾侧角符号为特征参数设计纵向、侧向预测模型，综合构成时变预测模型集，模型集根据目标历史运动规律、典型动作与任务环境实时更新，提高了未知机动适应能力。然后综合攻击意图与行为意图设计意图代价函数，在此基础上，通过贝叶斯理论推导机动模式与攻击意图的后验概率，并据此对多模型、多意图进行融合实现轨迹预测，提高了轨迹预测准确性与鲁棒性。

1 高超声速滑翔飞行器模型

假设高超声速滑翔目标侧滑角为零，忽略地球自转与扁率，其在半速度坐标系下的动力学模型为：

式中：r为地心距；λ和ϕ分别为经度、纬度；V为飞行速度大小；θ和ψ分别为弹道倾角与航向角；g为重力加速度大小；σ为倾侧角；L和D分别为升力加速度与阻力加速度大小，其计算公式为：

式中：m为飞行器质量；ρ为大气密度；S为飞行器特征面积；CL和CD分别为升力系数与阻力系数，是关于攻角α和马赫数Ma的函数。

高超声速滑翔飞行器控制量为攻角与倾侧角。攻角的主要作用是提供气动力，维持飞行器的稳定飞行；而倾侧角的主要作用是通过改变升力方向，实现飞行器机动飞行。由于非合作目标的气动系数、质量与参考面积是未知的，在滤波模型中，气动参数按下式计算：

式中：uL为升力参数；uD为阻力参数。二者与倾侧角σ共同构成高超声速滑翔目标的控制变量。跟踪过程中，将3个控制变量建模为一阶马尔可夫过程：

式中：λL，λD与λσ分别表示升力参数、阻力参数与倾侧角的机动频率；ωL，ωD与ωσ表示对应的过程噪声。

综合式（1）与式（4）构成滤波模型，通过扩展卡尔曼滤波（EKF）对控制规律进行辨识，实现对目标的跟踪估计。

2 预测模型集

高超声速滑翔飞行器一般采用纵向、侧向解耦控制。纵向需满足动压、过载、热流以及航程、终端高度等约束，通过设计攻角方案与倾侧角剖面来实现。侧向需满足规避禁飞区、指向意图以及机动动作等约束，一般通过设计倾侧角符号翻转逻辑来实现。侧向机动不消耗能量，也无法增加航程，它通过倾侧角符号翻转来满足地理约束，提升突防能力。综上，以升力参数、阻力参数与倾侧角幅值为特征参数，设计纵向机动模型；以倾侧角符号为特征参数设计侧向机动模型，综合构成高超声速滑翔飞行器预测模型集，模型集根据目标飞行状态与任务环境在线更新，从而提高机动目标预测能力。

2.1 纵向预测模型

高超声速滑翔飞行器的纵向机动特性由攻角方案与倾侧角剖面共同确定。攻角一般设计为关于最大攻角和最大升阻比攻角的分段方案，变化幅度较小。根据式（3），升力参数与阻力参数也呈现出分段特点，且变化幅度较小。倾侧角剖面中倾侧角幅值变化连续且变化幅度较小。因此，目标历史控制规律辨识是其控制规律预测的重要参考。

基于目标控制规律的辨识结果，通过最小二乘法进行滑窗拟合得到：

由于辨识过程中存在滤波误差，在预测过程中假设升力参数、阻力参数与倾侧角幅值均满足以拟合预测结果为均值的高斯分布，即：

综上，根据式（6）可生成nv组纵向特征参数，从而构成高超声速滑翔飞行器的纵向预测模型集{Mv1，…，}。

2.2 侧向预测模型

高超声速滑翔目标再入过程中主要有规避禁飞区（地缘政治限制或威胁规避）等地理约束以及攻击意图等终端约束。在满足以上约束的前提下，高超声速滑翔目标通常采用C 型与S 型2 种侧向机动模式，以增强突防能力。因此针对以上4 种典型动作设计侧向预测模型。

（1）攻击意图模型

当高超声速滑翔飞行器处于攻击意图状态时，倾侧角符号由高超声速滑翔飞行器与其意图之间的视线角ψηT确定，其计算公式如下：

式中：(λk，ϕk)表示k时刻高超声速滑翔目标的经度、纬度；(ληT，ϕηT)表示意图ηT的经度、纬度。

根据视线角设计航向角走廊为：

式中：δψ表示航向角误差门限。

根据意图航向角走廊确定倾侧角符号：

（2）规避禁飞区模型

当高超声速滑翔目标规避禁飞区时，航向角走廊根据目标当前位置、意图与禁飞区的相对关系确定。如果目标与意图在禁飞区的同一侧，即满足：

式（11）中第1 种情况表示目标与意图均在禁飞区的西侧，此时目标攻击意图不需经过禁飞区，因此禁飞区对目标状态无影响。同理，当目标与意图均在禁飞区的东侧、南侧与北侧时，分别对应式（11）中第2、3、4种情况，禁飞区对目标状态同样无影响。当不满足式（11）中4 种情况，高超声速滑翔目标受到禁飞区影响。考虑禁飞区的航向角走廊如图1所示，图中与分别表示目标当前位置与禁飞区φM的2个切线角，其计算公式如下：

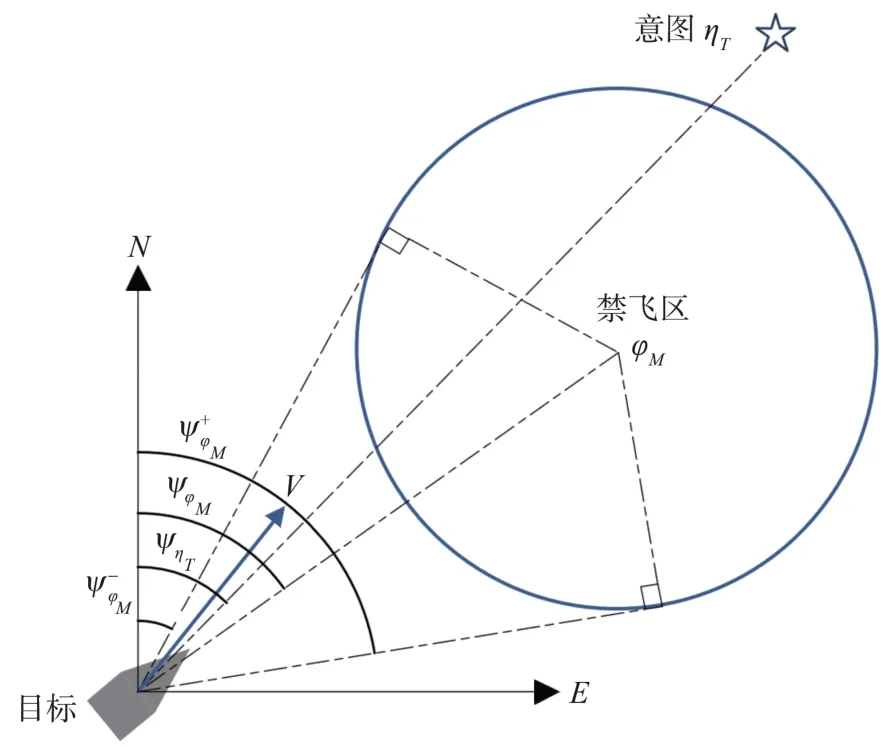
图1 航向角走廊示意图Fig.1 Schematic diagram of heading angle corridor

考虑所有禁飞区φM∈Ψ，航向角走廊为：

则根据禁飞区航向角走廊设计倾侧角符号翻转逻辑：

（3）C型机动模型

当目标做C 型机动时，高超声速滑翔目标朝一个方向进行转弯，以最大化机动范围。该机动模式下倾侧角符号保持不变，即：

（4）S型机动模型

当目标做S 型机动时，高超声速滑翔目标做多次转弯，即摆动动作，以最大化机动能力，因而倾侧角符号不断翻转。此时倾侧角符号设计为：

针对以上4 种典型动作设计侧向特征参数，构建目标的侧向预测模型集{Ml1，…，Ml4}。综合纵向、侧向预测模型，形成高超声速滑翔目标的时变预测模型集。

注1.纵向运动特征参数规律性强且变化幅度较小，通过最小二乘法与高斯随机过程实现了历史控制规律挖掘与未来未知机动探索的结合。侧向运动特征参数规律性弱且与历史无关，针对典型动作进行设计，实现了目标状态与任务环境的交互。综合纵向、侧向模型形成时变预测模型集，在线自适应更新，既提高了对目标机动的适应能力，降低了预测模型误差，又避免了蒙特卡洛预测［18］的复杂计算。

3 高超声速滑翔目标轨迹预测

3.1 意图代价函数

对于高超声速滑翔飞行器，其攻击意图的主要影响因素有飞行器与攻击意图的相对距离、航向误差角与意图价值。此外，在飞行过程中还需考虑规避禁飞区等行为意图。综合以上因素，构建意图代价函数，进而实现意图推断。

（1）攻击意图

通过解算高超声速滑翔飞行器可达区，确定可达意图ηT∈Θ。针对意图ηT计算代价函数。

①距离代价

式中：Idis，k表示高超声速滑翔目标当前位置与意图ηT之间的距离代价。距离代价表征了高超声速滑翔目标从当前位置攻击拟定意图需要的航程成本。距离越远，距离代价越大，相应意图的概率越小。

② 航向角代价

航向角代价表征了目标以当前速度方向攻击拟定意图需要的方向成本。航向角代价越大，说明攻击意图ηT的转弯成本越大，因而意图概率越小。

③意图价值

式中：WT表示意图ηT的价值，意图价值表征了意图对高超声速滑翔目标的吸引程度。意图价值越高，相应的意图概率越大。

（2）行为意图

目标行为意图主要考虑禁飞区的影响，禁飞区约束如图2 所示，禁飞区φM对目标行为意图的影响定义为：

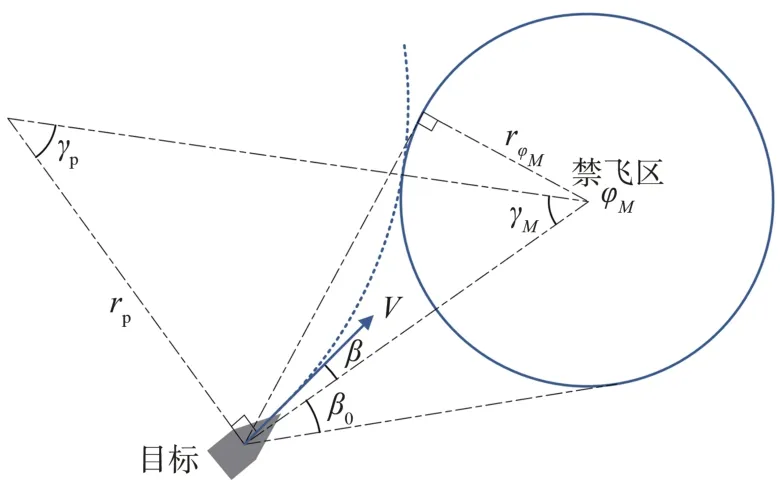
图2 禁飞区约束示意图Fig.2 Schematic diagram of no-fly zone constraints

式中：β0表示目标与禁飞区中心连线和切线的夹角；β表示目标与禁飞区中心连线和目标当前速度方向的夹角。当目标以当前速度恰好从禁飞区边缘飞过，即目标转弯圆与禁飞区相切时，获得目标与禁飞区最小距离，记为。

根据正弦定理与内角和定理，有：

式中：rp表示目标瞬时转弯半径，其计算公式如下：

注2.相对距离与相对方向是禁飞区意图代价的2个关键因素，如式（24）所示，禁飞区意图代价由相对距离比与速度误差角2 部分构成。速度误差角越大，目标速度越指向禁飞区中心，目标穿过禁飞区概率越大，意图代价相应增加。当时，目标瞬时转弯圆与禁飞区恰好相切，此时相对距离比为1，故禁飞区意图代价只受速度误差角影响。当时，目标瞬时转弯圆与禁飞区相交，目标从禁飞区内部穿过的风险增大。此时禁飞区意图代价>β0-β。相 反，当相对 距离比小于1，即时，目标瞬时转弯圆与禁飞区相离，禁飞区意图代价减小。进一步，当时，即使存在速度误差角，由于目标瞬时转弯圆与禁飞区相离甚远，目标有足够的安全裕度绕过禁飞区，所以此时→0。

当存在多个禁飞区影响目标任务时，则在所有禁飞区中选取意图代价不为零且距离目标最近的禁飞区，以表征当前时刻的综合禁飞区意图代价，即：

综上，禁飞区意图代价为：

综合攻击意图与行为意图，定义意图代价函数：

式中：τ1、τ2与τ3为代价系数。

考虑到目标在整个飞行过程中攻击意图与行为意图具有连贯性，将意图代价函数构建为衰减自相关递推序列，即：

式中：ρ为衰减系数。

3.2 多模型多意图融合轨迹预测

当攻击意图ηT时，根据意图代价函数，其在机动模式uj下状态转移的似然概率定义为：

式中：K为归一化系数：

根据贝叶斯定理，机动模式uj的后验概率为：

由于状态转移过程具有马尔可夫性，上式可进一步简化为：

式中：Pr(xk|xk-1，ηT，uj)为机动模式uj的似然概率，根据其定义式（32）计算得到；Pr(uj|x1：k-1，ηT)为上一时刻机动模式uj的后验概率，通过迭代计算得到；Pr(xk|x1：k-1，ηT)表示意图ηT的似然概率，其计算公式如下：

进一步，根据贝叶斯定理，意图ηT的后验概率计算公式如下：

根据全概率公式，利用意图ηT的似然概率与后验概率对高超声速滑翔目标状态进行一步预测：

同理，递推得到多步预测的计算公式：

其中，状态转移似然概率计算公式为：

式中：第1 项为似然概率Pr(xk+j|xk+j-1，ηT)，根据式（36）计算得到；第2 项为意图后验概率。在预测阶段，观测信息缺失，依靠误差较大的预测信息进行意图推断难以保证准确性与可靠性，同时考虑到目标意图在飞行过程中不会频繁改变，因而高超声速滑翔目标的意图后验概率分布在预测阶段不再迭代更新，即：

注3.多模型多意图融合轨迹预测方法综合了基于运动机理与基于意图推断2 类轨迹预测方法的优势，以意图代价函数作为评价规则，基于贝叶斯理论推导多模型、多意图的融合规则，提高了长时轨迹预测的准确性与鲁棒性。

3.3 轨迹预测流程

由于目标轨迹连续且光滑，轨迹序列拟合预测短时精度较高。因此，为进一步提高数据利用率，在预测初期将高超声速滑翔目标的轨迹拟合预测结果引入预测方法进行修正，修正方案如下：

式中：ξ<1为一常数。轨迹拟合预测结果短时精度较高，但预测误差会急剧增加，因而w在初期为较大值，之后快速减小，以剥离拟合预测结果，避免引入拟合误差。

多模型多意图融合轨迹预测框图如图3 所示。轨迹预测步骤如下：

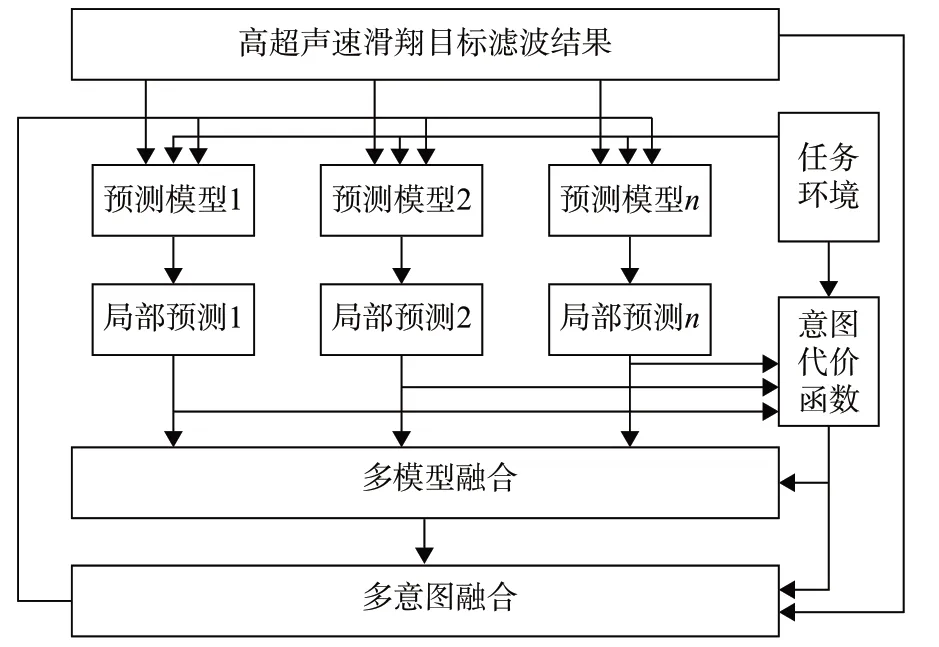
图3 多模型多意图融合轨迹预测框图Fig.3 Block diagram of trajectory prediction

1) 初始化

a）读取传感器参数、观测数据、禁飞区以及意图分布等数据；

b）初始化滤波状态及协方差矩阵、机动模式后验概率与意图后验概率等；

2) 预测模型集构建

a）通过EKF辨识高超声速滑翔目标控制规律；

b）根据式（6）可生成nv组纵向特征参数，构建纵向预测模型；

c）针对2.2 节中4 种典型动作设计侧向特征参数，构建侧向预测模型；

3) 意图推断

a）解算目标可达区，确定可达意图；

b）基于预测模型集进行预测，并根据式（31）计算局部预测结果与滤波结果的意图代价函数；

c）根据式（32）～（37）迭代更新意图后验概率；

4) 轨迹预测

a）将局部预测的意图代价函数代入式（32）计算状态转移似然概率；

b）根据式（35）计算预测模型的后验概率，并据此对多模型预测轨迹进行融合；

c）根据意图后验概率对多意图预测轨迹进行融合；

d）根据式（42）引入轨迹序列拟合预测结果进行修正，获取目标轨迹预测结果；

e）保存数据并返回2）进行下一次迭代更新。

4 仿真校验

为验证所提预测方法的有效性与优越性，以美国CAV-H［19］为典型目标开展仿真实验。该飞行器参考面积为0.483 9 m2，质量为907 kg。目标初始条件如表1所示。存在3个意图与2个禁飞区，其参数设置如表2 所示，3 个意图价值相同，其中意图1为飞行器真实意图。高超声速滑翔飞行器采用预测校正与倾侧角符号翻转逻辑进行制导［20-21］。传感器位于东经60°、北纬20°，测量量为距离、高低角与方位角。距离测量精度为10 m，高低角与方位角测量精度为0.01 rad，数据采样率为2 Hz。仿真中滑窗容量nw=400，放缩因子μ=0.8，纵向机动模型数nv=5，航向角误差门限δψ=5°，代价系数τ1=0.000 02，τ2=1，τ3=100，衰减系数ρ=0.1。

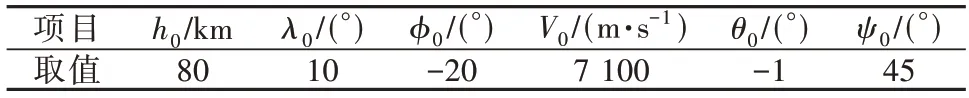
表1 目标初始状态Table 1 Initial states of the target

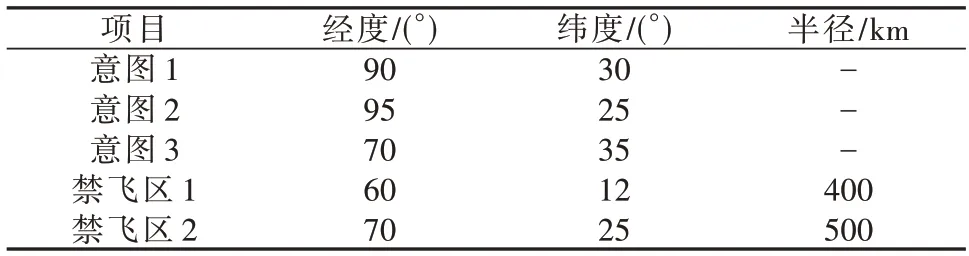
表2 意图与禁飞区参数Table 2 Parameters of intents and no-fly zones

设定倾侧角取值范围为[-90°，90°]，利用常值倾侧角法［22］解算高超声速滑翔飞行器可达区，结果如图4所示，3个意图均在可达区内。

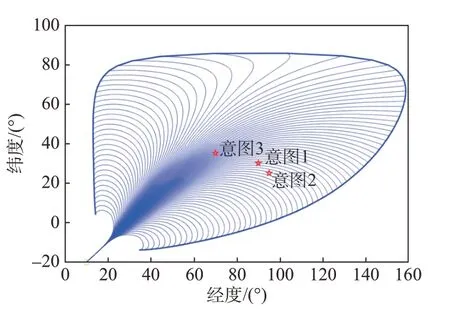
图4 高超声速滑翔飞行器可达区Fig.4 Reachable region of the hypersonic gliding vehicle

为验证本文所提预测方法的有效性与优越性，对文献［7］与文献［18］的轨迹预测方法进行仿真以作对比。为便于标记，以上2 种轨迹预测方法分别记为方法1与方法2，本文所提轨迹预测方法记为方法3。方法2中代价系数与方法3设置相同。

4.1 算例1

高超声速滑翔目标纵向采用准平衡滑翔模式，侧向做S型机动，同时规避禁飞区并飞向意图，其真实轨迹如图5所示。

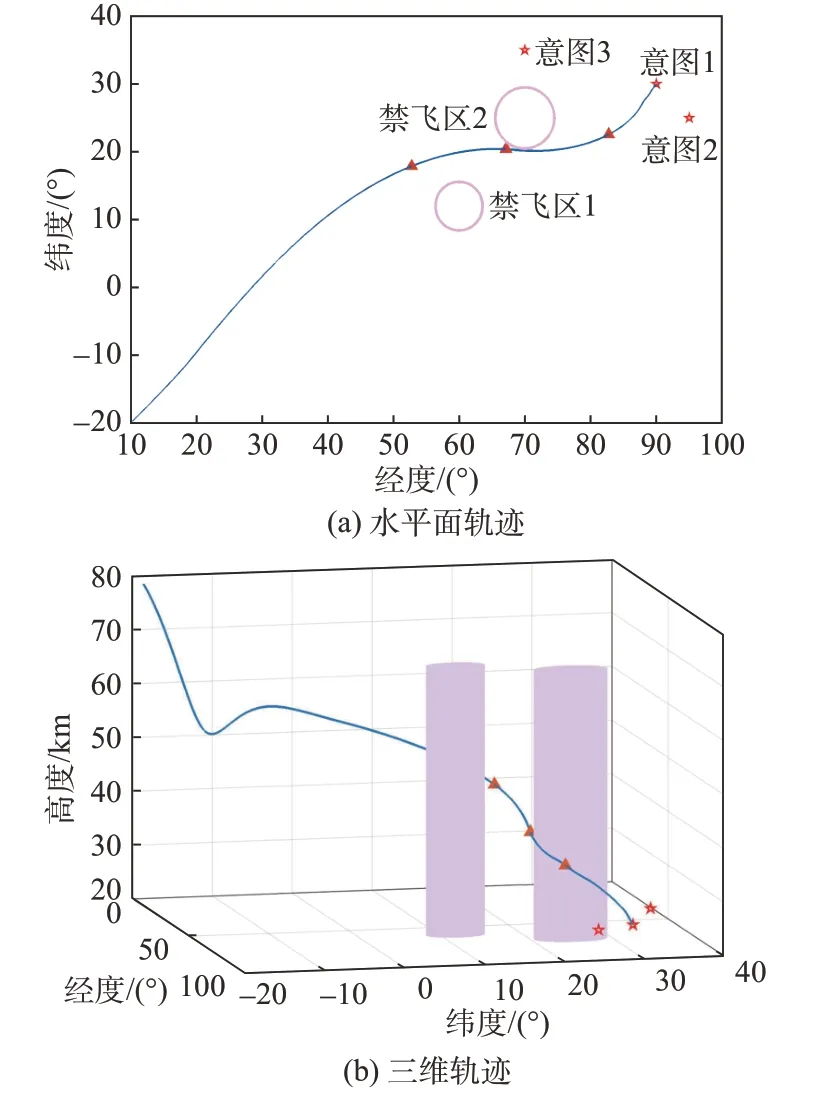
图5 高超声速滑翔飞行器真实轨迹Fig.5 Real trajectory of the hypersonic gliding vehicle

分别以1 000 s、1 300 s 与1 700 s 为起始点进行预测，以验证轨迹预测方法在接近禁飞区、经过禁飞区、攻击意图3 种典型情况下的预测性能，图5 中三角形标记了预测起始点。意图后验概率如表3所示，表中tpre表示轨迹预测起始时间。在tpre=1 000 s与tpre=1 300 s 时，由于受到禁飞区影响，飞行器在距离与角度方面都更倾向于意图2，因此意图2的后验概率相对较高。根据图5（a）中所示目标的轨迹变化趋势，此时将意图2 作为主要意图进行轨迹预测是合理的。当飞行器绕过禁飞区继续朝其真实意图（意图1）运动时，意图1 的后验概率逐渐增大，在tpre=1 700 s超过80%，明显高于其他意图。

表3 意图后验概率Table 3 Posterior probability of intents

从tpre=1 000 s 开始预测，预测时长200 s，水平面与竖直面内轨迹预测结果如图6 所示，对应的预测误差如图7所示。根据预测结果可知，方法1对控制变量的历史规律进行外推实现轨迹预测，在20 s内预测误差较小，之后随着时间推移，目标实际运动与历史运动偏差增大，预测误差显著增加。由于意图推断的修正作用，方法2与方法3在水平面内预测精度较高，相对方法1分别提高了61.39%、81.05%。在高度预测方面，方法3 结合历史规律与高斯过程构建纵向机动模型进行预测，同时叠加轨迹拟合预测结果的修正作用，获得了较高的预测精度。方法1 完全依赖历史运动规律，预测效果稳定性较差。由于方法2 假设飞行器高度为常值，而此时飞行器处于平衡滑翔状态，高度预测误差逐渐增大。

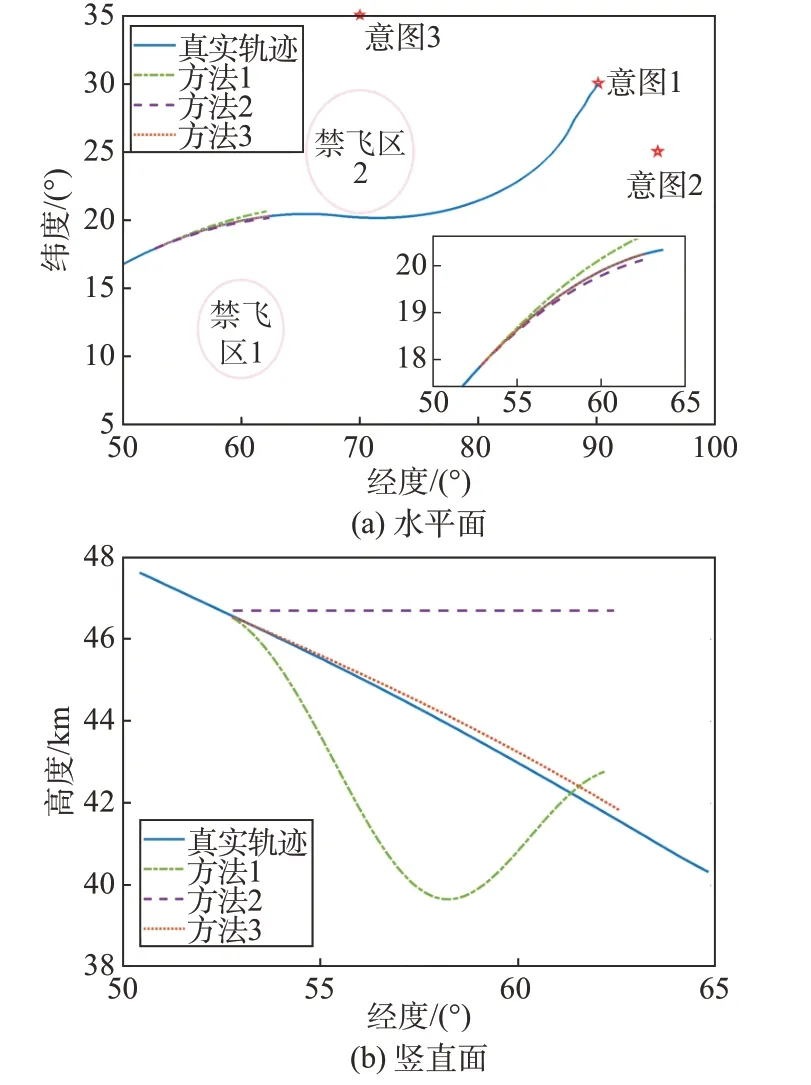
图6 预测轨迹（tpre=1 000 s）Fig.6 Prediction trajectory（tpre=1 000 s）

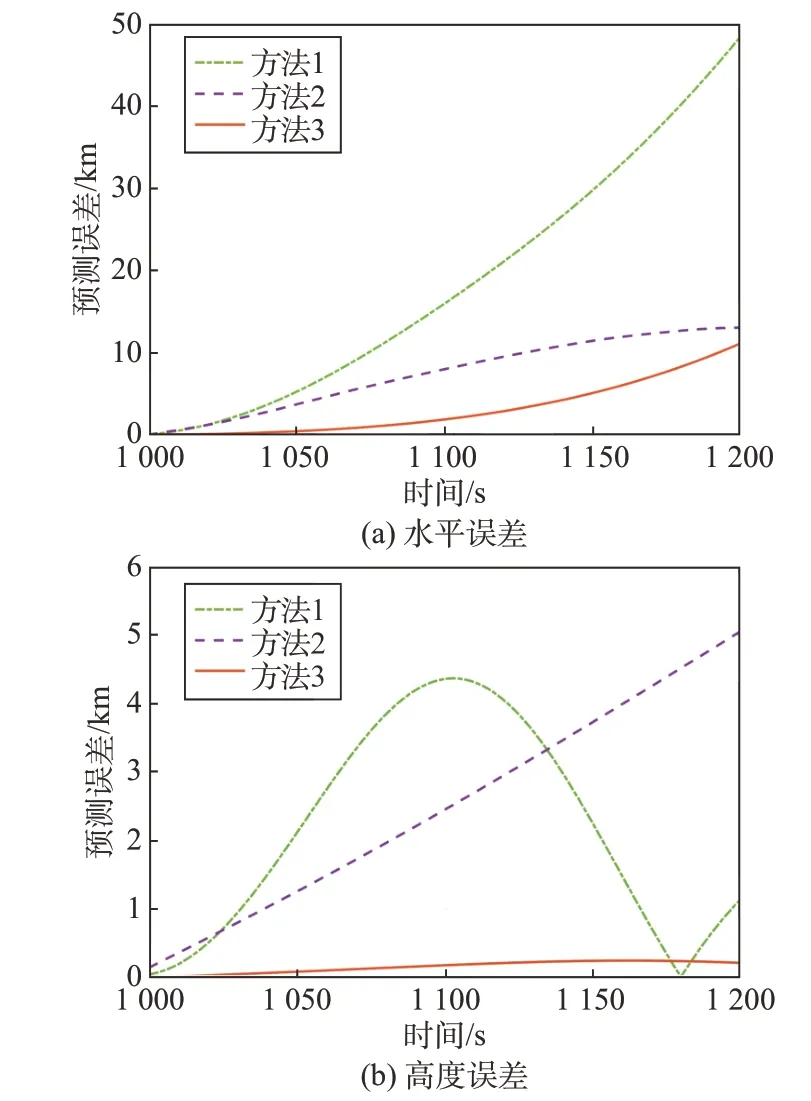
图7 预测误差（tpre=1 000 s）Fig.7 Prediction errors（tpre=1 000 s）

当tpre=1 300 s 时，预测结果如图8～图9 所示。预测初期飞行器主要任务为绕开禁飞区，之后朝其真实意图飞行。根据图9（a）可得，3 种预测方法在前80 s 的预测误差相对较小，这是由于此阶段飞行器经过了禁飞区最近点，倾侧角符号发生偏转，因此预测误差呈现出先增大后减小的特点，但是飞行器侧向机动范围较小，因而整体预测误差尚可。在80 s 后，飞行器开始朝向真实意图飞行，观察图8 发现，方法1不具备意图推断能力，依赖历史信息进行预测，显然其预测模型偏离了飞行器真实运动模型，导致在水平与高度上均出现了较大偏差。方法2 在飞行器可达集范围内通过蒙特卡洛采样进行预测，根据图8（a）可以看出，在规避禁飞区后未能及时调整倾侧角符号，导致侧向预测误差逐渐增大。基于高度不变假设，正值此时飞行器下降缓慢，方法2 在高度上预测精度较高。相比之下，方法3 预测精度优势明显，尤其是侧向预测方面，体现出了较强的机动自适应能力。

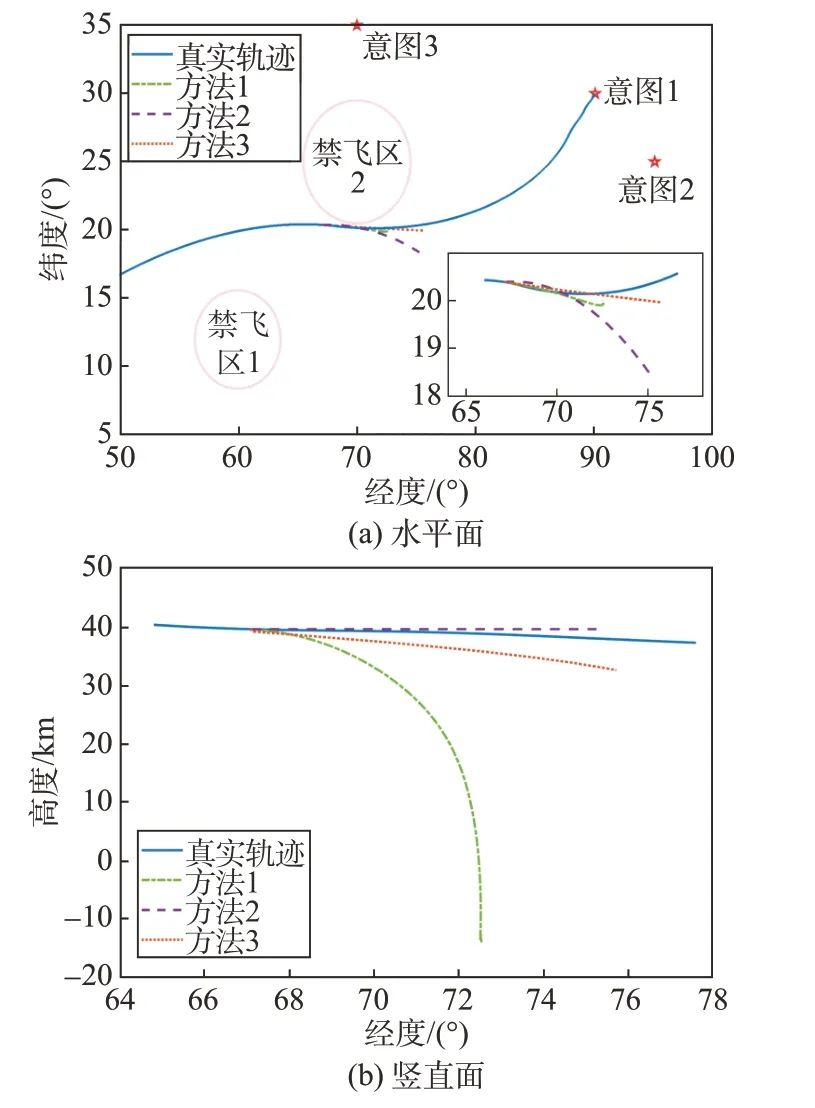
图8 预测轨迹（tpre=1 300 s）Fig.8 Prediction trajectory（tpre=1 300 s）

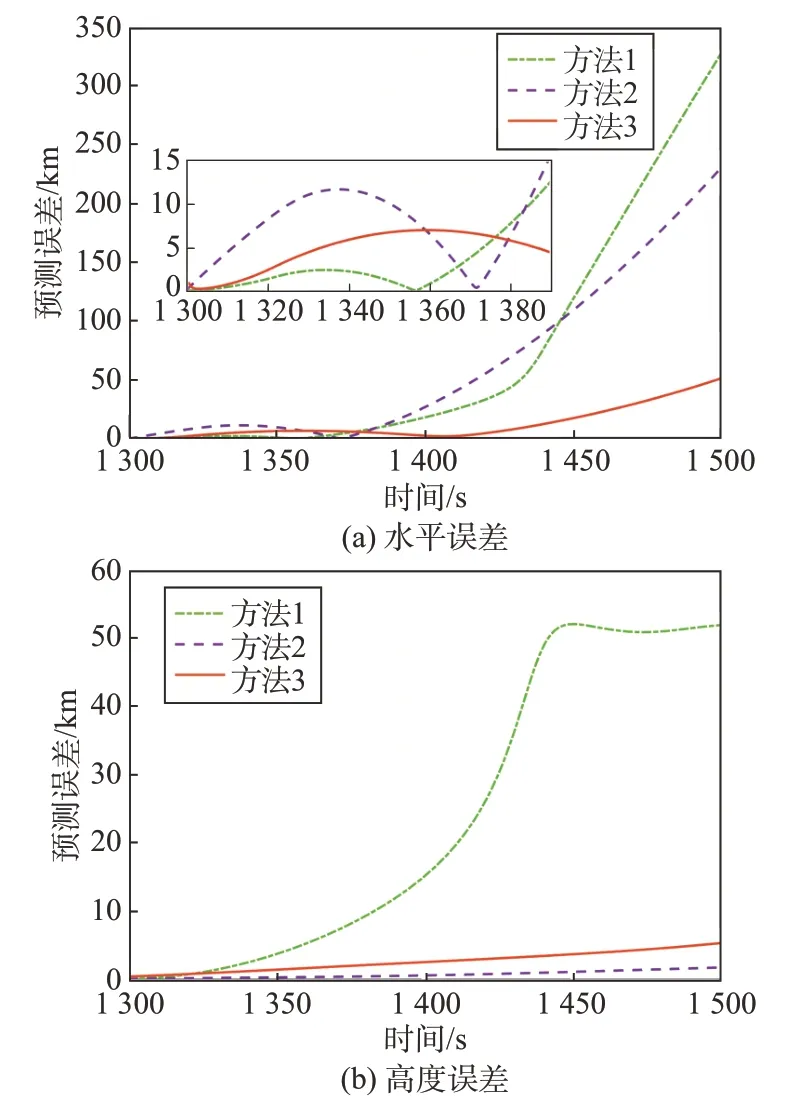
图9 预测误差（tpre=1 300 s）Fig.9 Prediction errors（tpre=1 300 s）

以tpre=1 700 s为起始时刻的预测结果如图10～图11 所示，仿真结果表明，本文提出的多模型多意图融合轨迹预测方法的预测精度高于方法1与方法2。以上3种情况的综合预测误差与计算时间如表4所示。方法1类似于开环控制，计算速度快，但精度无法保证。方法2 与方法3 通过意图推断提高了预测精度，但增加了计算时间。该类方法依赖于意图推断的准确性。由于方法2基于可达集区域离散进行预测，计算量较大，耗时相对较长。

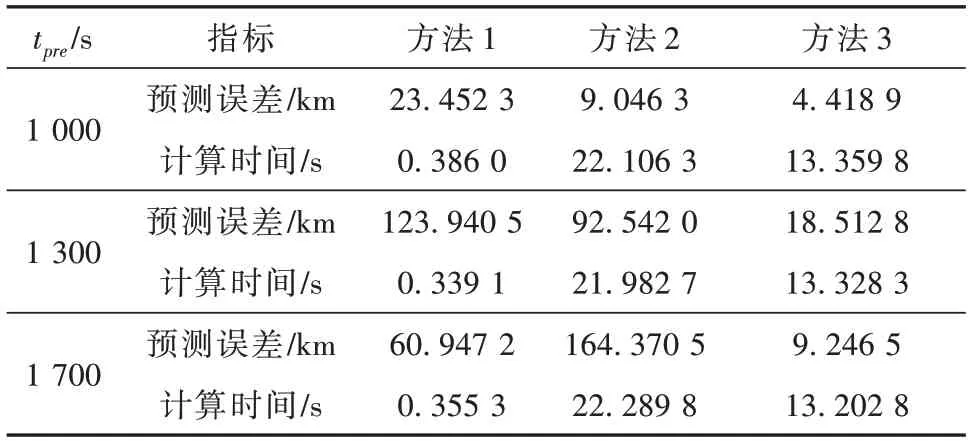
表4 预测方法对比Table 4 Comparison of prediction methods

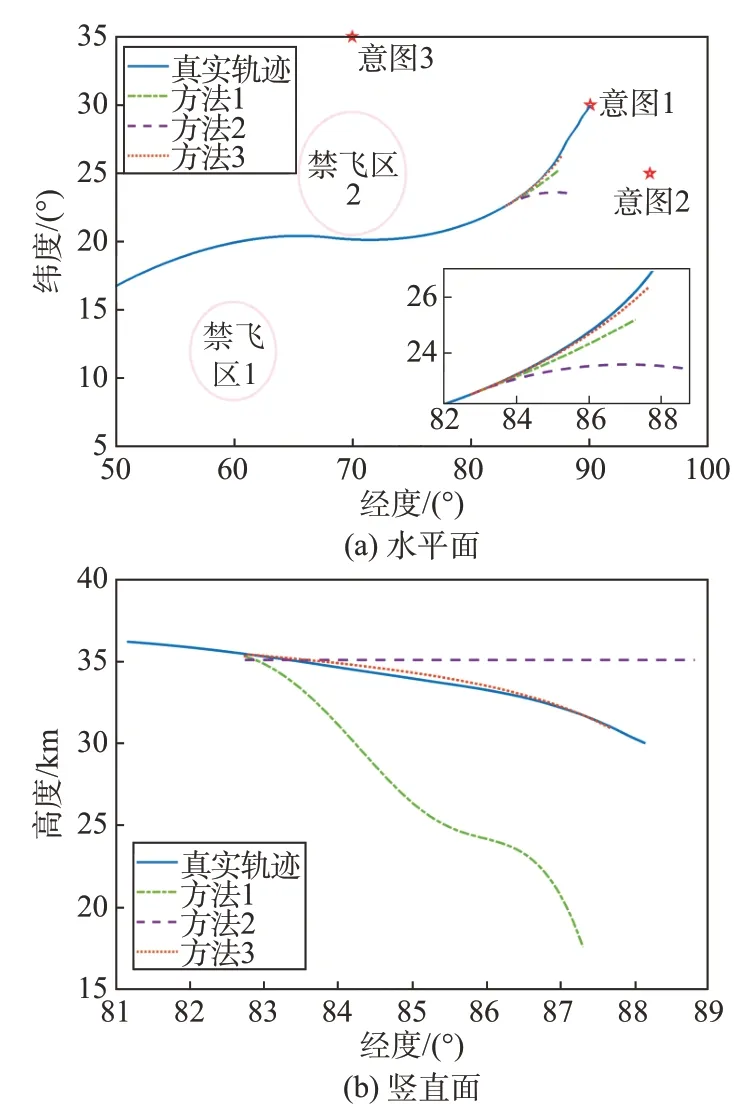
图10 预测轨迹（tpre=1 700 s）Fig.10 Prediction trajectory（tpre=1 700 s）

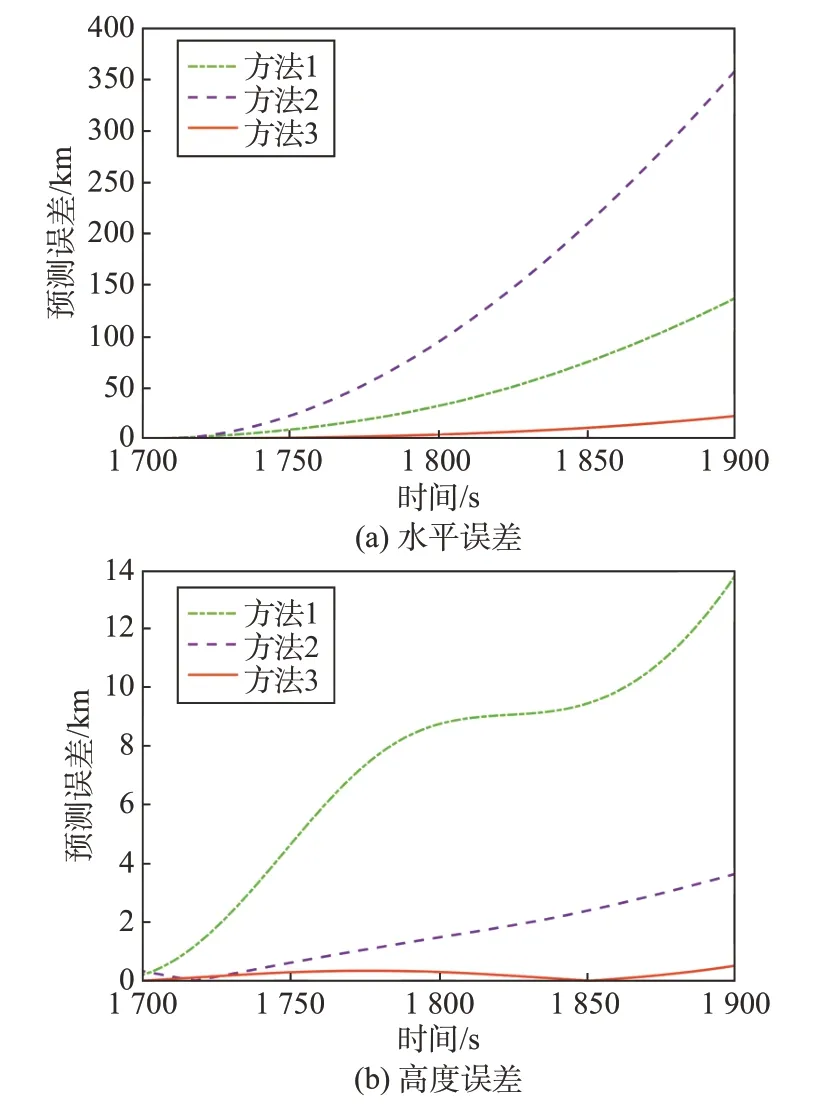
图11 预测误差（tpre=1 700 s）Fig.11 Prediction errors（tpre=1 700 s）

4.2 算例2

目标纵向采用跳跃滑翔模式，侧向做C 型与S型机动，同时规避禁飞区并指向意图，其真实轨迹如图12所示。分别在1 200 s、1 400 s与1 800 s开始预测，对应的意图后验概率如表5 所示。在1 500 s之前意图1 与意图2 尚未分明，因此概率几乎持平。之后飞行器朝向其真实意图飞行，意图1相对距离、航向角度优势逐渐明显，对应概率逐渐提高。

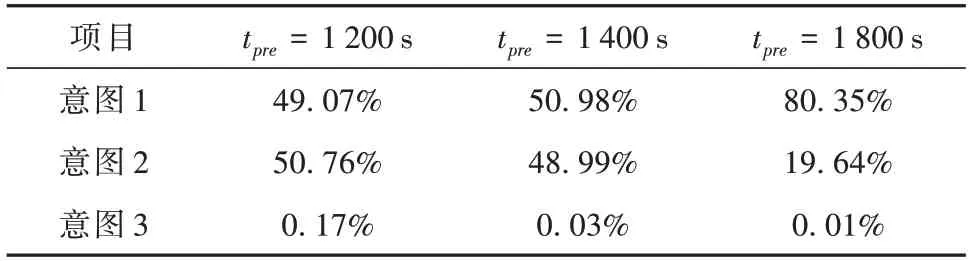
表5 意图后验概率Table 5 Posterior probability of intents

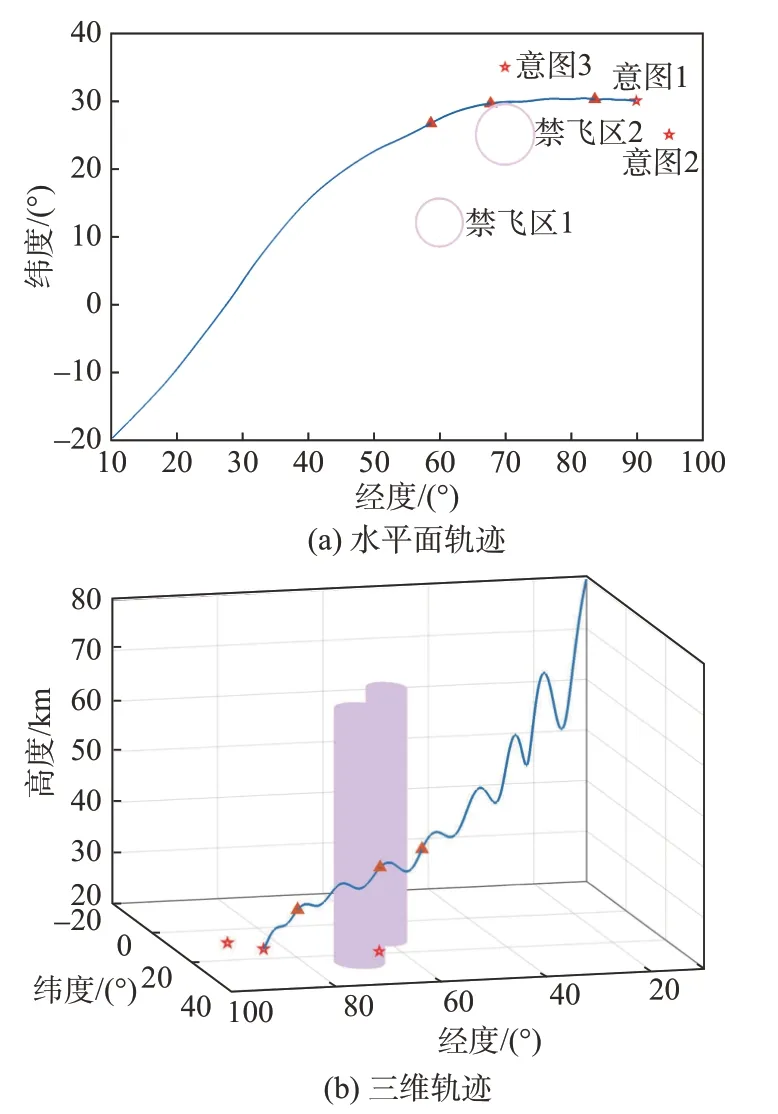
图12 高超声速滑翔飞行器真实轨迹Fig.12 Real trajectory of the hypersonic gliding vehicle

从tpre=1 200 s 开始向后预测200 s，轨迹预测结果如图13 所示，对应预测误差如图14 所示。由图可得，方法1 在前20 s 预测误差较小，之后随着预测模型的偏离，预测误差急剧增大。方法2与方法3预测精度远高于方法1。在高度方面，方法3有效预测了飞行器的跳跃弹道特性，但是预测模型误差依然存在。而方法2 高度维持不变，与高超声速滑翔目标的真实跳跃弹道先远离后接近。

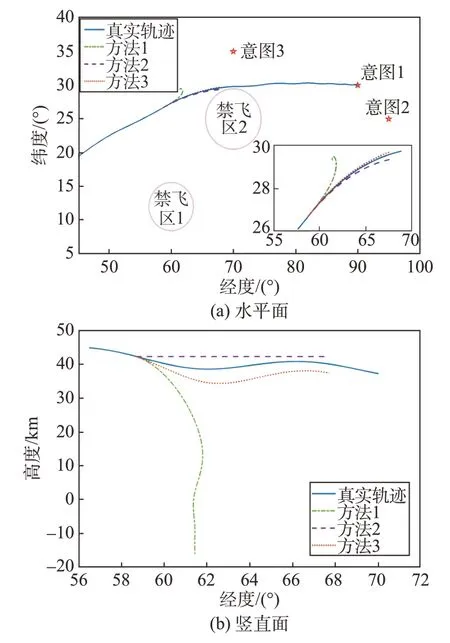
图13 预测轨迹（tpre=1 200 s）Fig.13 Prediction trajectory（tpre=1 200 s）

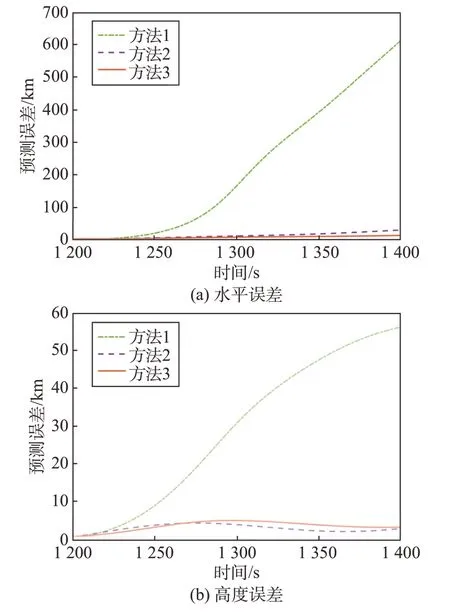
图14 预测误差（tpre=1 200 s）Fig.14 Prediction errors（tpre=1 200 s）

以1 400 s、1 800 s 为起始时刻的预测结果如图15～图16 所示。根据图16（a），在攻击意图过程中，目标侧向做S 型机动，方法1 与方法2 未能及时调整倾侧角符号，导致逐渐偏离真实轨迹，水平预测误差显著增大。方法3 通过侧向机动模式集，实现了倾侧角符号的在线调整，预测误差因延迟呈现出波动特征，但误差始终较小。

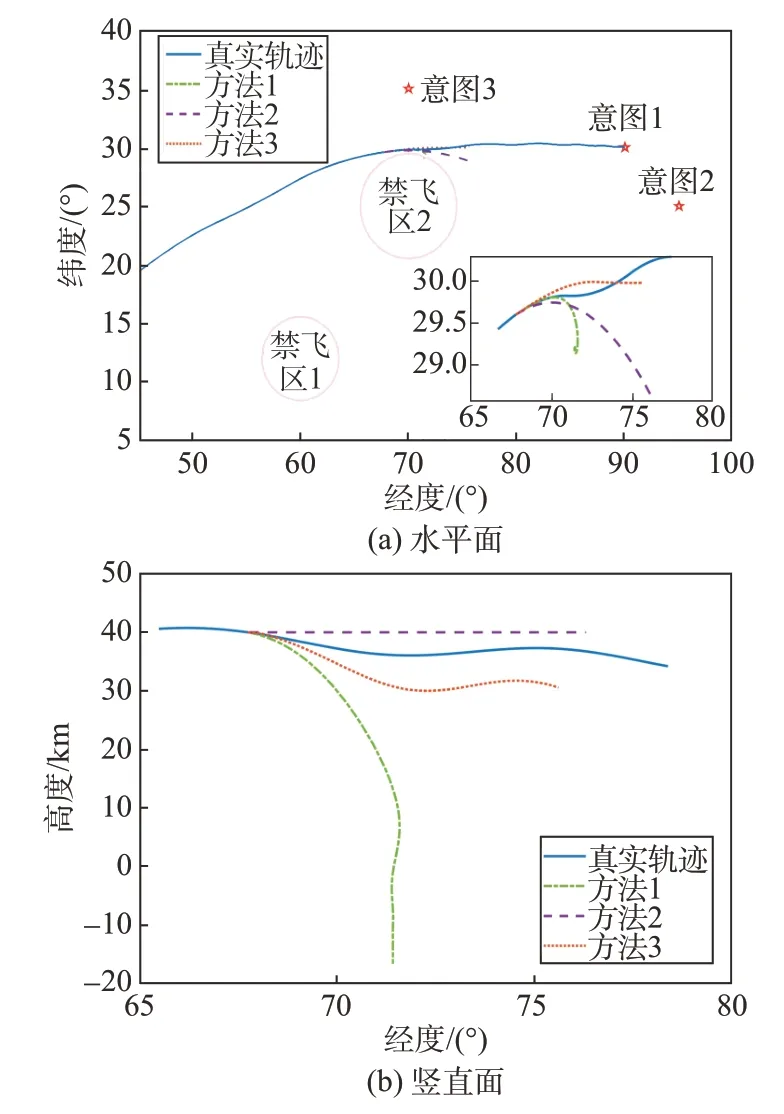
图15 预测轨迹（tpre=1 400 s）Fig.15 Prediction trajectory（tpre=1 400 s）

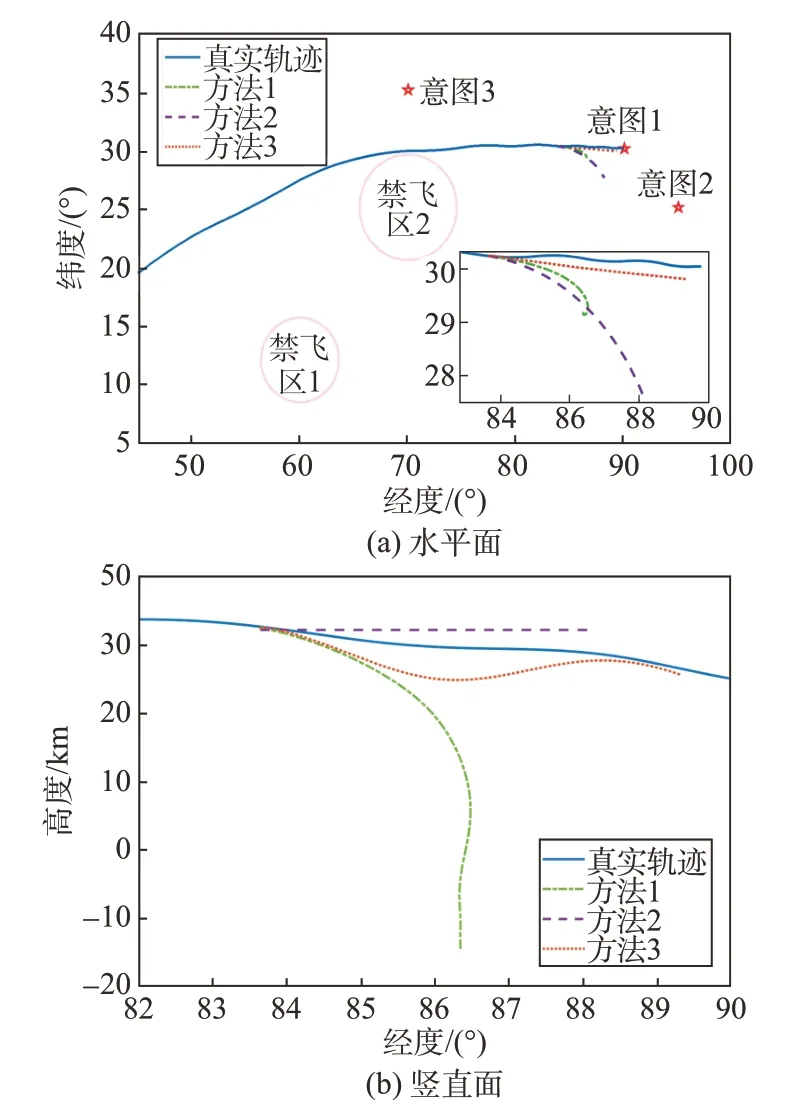
图16 预测轨迹（tpre=1 800 s）Fig.16 Prediction trajectory（tpre=1 800 s）

3 种情况的轨迹预测指标如表6 所示。计算时间方面方法1 用时最短，方法3 次之，方法2 用时最长；预测误差方面方法3最小，方法2次之，方法1误差最大。由于需要意图推断解算，方法2 与方法3总计算时间较长。但是考虑到攻击意图具有稳定性，2 种方法的意图概率在预测阶段不进行迭代更新，在实际应用中，意图推断可以在跟踪阶段解算完成，因此方法2 与方法3 的纯预测解算时间约为3 s与1 s。在可接受时间成本下，方法3 在预测精度方面具有显著优势。

表6 预测方法对比Table 6 Comparison of prediction methods

5 结论

基于模型交互与意图推断思路，提出了一种基于贝叶斯理论的多模型多意图融合轨迹预测方法，提高了高超声速滑翔目标长时轨迹预测的准确性与鲁棒性。基于控制规律挖掘与典型机动动作，针对纵向、侧向运动构建时变预测模型集，结合目标状态与任务环境在线自适应更新，提高了对目标未知机动的适应能力。综合攻击意图与行为意图设计了意图代价函数，基于贝叶斯理论推导了机动模式与攻击意图的后验概率，通过多模型、多意图双层次融合提高了轨迹预测精度，进一步适应长时预测需求。仿真结果表明，本文提出的轨迹预测方法能够有效应对高超声速滑翔目标的准平衡滑翔、跳跃滑翔、C 型、S 型等复杂机动，与已有方法相比，具有更好的预测精度。