高超声速滑翔飞行器多模型鲁棒跟踪方法

王瑞鹏，王小刚，张豪杰

（1.哈尔滨工业大学航天学院，哈尔滨 150001；2.北京电子工程总体研究所，北京 100854）

0 引言

随着跟踪、预报以及拦截等反导技术的快速发展，弹道形式相对固定的传统弹道导弹已经难以突破现有的导弹防御体系，近年来，高超声速滑翔飞行器（Hypersonic gliding vehicle，HGV）凭借其大升阻比的外形，可在临近空间环境内以超过5 的马赫数实现远距离滑翔及大范围机动，成为工程研究的重点，现已开展多次HGV 飞行试验［1-2］。HGV 对现有的导弹防御体系造成了极大的压力，对HGV 的跟踪难点在于其弹道形式多样，在滑翔段可以以平衡滑翔或跳跃滑翔方式飞行［3］，因此难以对其进行准确建模。此外，HGV 在临近空间内高速飞行产生时变的等离子鞘套，对地基雷达的探测过程也产生了较大影响，使得探测噪声呈现出非高斯分布的特性［2］。因此，在非高斯噪声条件下研究临近空间HGV 轨迹跟踪方法就显得格外重要。

为解决HGV 的轨迹跟踪问题，一个重要的方面就是如何建立符合HGV 运动特点的目标运动模型，目前的研究方向主要分为两个方向，分别是基于动力学的跟踪方法以及基于运动学的跟踪方法。基于动力学的跟踪方法其主要思想是对未知的气动参数进行辨识，即将气动参数增广到状态方程中，基于气动力模型对HGV 进行跟踪［4-5］。魏世君等［6］根据天基红外卫星的测量信息设计了机动观测器，对未知的气动加速度进行估计，并分析了观测器的误差界。文献［7］将气动加速度建模为Singer模型，同时利用正交原理判断建模误差，自适应修改模型的机动频率。但此类方法的跟踪精度严重依赖于气动参数的辨识结果，并往往需要目标更多的先验信息，当气动力变化较快或先验信息与实际相差较大时难以保证估计精度，因此在工程中通常难以直接应用［8］。在运动学方面，常用的假设加速度为常值的常加速度（CA）模型、Singer模型、对加速度进行自适应的“当前”统计模型（Current statistical model，CSM）以及对加加速度进行估计的Jerk 模型均难以准确描述HGV 的运动特点。针对HGV 的周期性的跳跃滑翔式运动，王国宏等［9］将加速度建模为具有正弦波自相关的零均值过程，进而提出了SW（Sine wave）模型，该模型合理的描述了HGV 运动的周期性特征。文献［10-11］将加速度的均值假设为正弦自相关随机过程，并利用一阶或二阶马尔可夫过程对机动进行补偿，进而提出了自适应非零均值衰减振荡（ANMDO）模型，该模型同时响应了HGV 跳跃滑翔阶段的周期性和衰减性的特点，是目前描述HGV 跳跃滑翔运动较为准确的运动学模型。

由于单模型方法难以匹配HGV 的多种运动情况，目前的研究重点在如何建立合适的目标运动模型集以及研究基于多模型滤波结构的跟踪方法上［12］，文献［13］基于Singer、CA 和CT 模型建立了交互式多模型（Interacting multiple model，IMM）跟踪滤波器以实现对HGV 的跟踪。文献［14］利用多个机动角速率不同的Sine 模型对HGV 的跳跃滑翔运动进行匹配。文献［15］则在模型集中同时加入了动力学模型和运动学模型，利用多模型方法融合了动力学模型建模匹配程度高和运动学适应性强的优点。考虑到固定结构多模型算法模型集固定且各模型之间存在竞争导致精度下降的问题，文献［16］利用自适应网格变结构多模型对结构和模型参数进行自适应调整。文献［17］在变结构多模型的基础上利用有向图切换的方法对SW 模型的周期机动角速度进行自适应切换，以实现对HGV 滑翔段的有效跟踪。

有关HGV 轨迹跟踪，另一个重要的研究方面是非线性滤波方法。在HGV 的跟踪系统中状态方程和量测方程均具有较强的非线性，因此在工程应用中常常使用扩展卡尔曼滤波（EKF）对其进行跟踪，但由于EKF 存在较大的截断误差，导致其跟踪精度有限。因此学者们逐渐采用基于确定性采样的非线性滤波方法进行跟踪滤波器的设计，包括基于径向容积规则的容积卡尔曼滤波（CKF）和基于无迹规则的无迹卡尔曼滤波（UKF）［18-19］。但是，上述方法均是在噪声符合高斯分布的假设下进行推导的，当探测噪声呈现非高斯特性时，这些算法的精度会严重下降甚至发散。在处理非高斯噪声问题方面，最常用的鲁棒滤波方法为基于广义极大似然的Huber滤波，该方法通过混合l1和l2范数的组合以获得对量测异常值的有效抑制［20］，其对闪烁噪声具有良好的渐进最优鲁棒性能。文献［21］将Huber滤波与五阶CKF 进行了融合，提出了HCHF 用于助推段轨迹的跟踪。文献［22］在Huber滤波处理量测噪声模型存在误差问题的基础上，将UKF 与强跟踪方法相结合，用于跟踪存在倾侧角反转的HGV 目标。近年来，也有学者利用学生t 分布［23］或高斯混合模型［24］对重尾分布的噪声进行建模，并利用变分贝叶斯方法对噪声模型的参数进行实时估计以适应先验信息的不准确性。虽然这种方法可以得到较高的估计精度，但需要利用不动点迭代的方法进行多次运算［25］，往往伴随着更大的计算量。

综上所述，对临近空间HGV 轨迹跟踪的难点在于目标机动形式复杂多变且机动时机不确定造成的目标运动模型建模困难，以及非高斯噪声条件下非线性滤波跟踪方法精度难以保证。因此本文首先设计了基于有向图切换的多模型滤波结构，在传统交互式多模型算法的基础上，利用有向图切换的方法实现模型集结构及参数的自适应调整；其次，将Huber 滤波方法与CKF 相结合，利用Huber 滤波实现对非高斯噪声的鲁棒性并应用CKF 处理跟踪系统的强非线性；然后，采用不同衰减频率的ANMDO 模型对HGV 跳跃滑翔阶段进行近似，同时利用不同机动频率的“当前”统计模型描述平衡滑翔运动并建立了目标运动模型集，之后基于地基雷达的量测模型完成HGV 跟踪方法的设计；最后利用数学仿真的方法对所提算法进行了验证。

1 基于有向图切换的变结构多模型结构

HGV 在滑翔段具有跳跃滑翔和平衡滑翔两种常用的飞行模式，传统的单模型方法无法适应这种机动样式复杂多变的情况，因此需要利用多模型方法以实现有效跟踪。最常见的多模型方法即交互式多模型方法，以其结构简单、计算效率高等优点在工程中得到了广泛的应用。但对于HGV 来说，覆盖所有可能的机动样式会导致模型集过于庞大，不仅导致计算成本急剧增加，而且由于模型集之间的模型竞争又会导致跟踪精度下降［26］，因此需要采用变结构多模型对其进行改进。本文基于有向图的思想，在IMM 的基础上利用有向图切换的方式对实时模型集进行自适应调整，在保证对HGV 机动样式覆盖性的同时缩短了算法运行时间。

1.1 交互式多模型结构

考虑如下的非线性多模型状态空间系统：

式中：k为离散的时间序列；xk∈Rn为n维的状态向量；yk∈Rm为m维的量测向量；f(·)和h(·)分别代表非线性的状态方程和量测方程；wk和vk分别代表过程噪声和量测噪声；mk∈{1，…，M}为模型标识；(·)代表此时第mk个状态模型正在生效；mk符合马尔可夫过程，即：

式中：pij为模型i到模型j的转移概率，可由经验确定或由自适应算法进行调整。

作为多模型算法中最经典的算法，IMM 通过设计一个覆盖目标所有可能运动情况的固定模型集，每个模型独立运行在各自的子滤波器中，并且各子模型在输入时进行数据的相互作用完成交互，当子模型得到各自的估计结果后，根据似然函数计算相应权值并将所有子滤波器的状态估计结果进行加权融合，作为多模型的滤波结果实时输出，其具体步骤如下。

交互式多模型算法首先根据上一时刻各子滤波器的估计结果进行交互计算，得到当前时刻子滤波器的输入，包括各子模型的先验模型概率、状态和误差协方差。对于第j个子模型的先验模型概率

式中：uk-1[i]=p(mk-1=i|y1：k-1)为上一时刻第i个模型的后验模型概率。

对于第j个子模型的状态先验概率p(xk-1|mk=j，y1：k-1)，有：

假设各子模型的后验概率均符合高斯分布，则第j个子模型输入的初始状态均值和协方差分别为

随后各子滤波器利用当前时刻的量测信息独立并行进行滤波更新，获得各自的状态估计、误差协方差、新息以及新息协方差矩阵S(j)。计算似然函数对模型概率uk[j]进行更新：

式中：N(μ；0，σ)表示高斯分布。

最后IMM 通过融合各子滤波器的估计结果获得最终的状态估计，假设第j个子模型的估计结果为

1.2 有向图切换方法

变结构多模型在IMM 的基础上，提出了模型总集和实时模型集的概念。假设模型总集为ΘM，实时模型集为Θk∈ΘM，变结构多模型是通过某种的模型集自适应策略，在总模型ΘM中找到可描述目标当前运动状态的最小模型集Θk，并将Θk作为实时模型集运行IMM 算法得到机动目标的状态估计。基于有向图切换的变结构多模型方法为通过可能模型集的设计，完成对总模型集ΘM的完全覆盖，并使得相邻的两个可能模型集中存在重复的模型，同时保证各可能模型集不完全相同，通过判断边缘模型的实时模型概率是否超过阈值，从而确定是否对实时模型集进行切换。

如图1 所示，首先预制数个具有相同模型数量的可能模型集Θ={Θ1，Θ2，…，Θm}，可能模型集中包含位于中心位置的中心模型和边缘模型，可见各子模型集的中心模型同时为相邻模型集中的边缘模型，如果当前模型集Θk中的某一边缘模型mj的后验模型概率大于所设定的阈值λ，则实时模型集向以模型mj为中心模型的可能模型集移动，从而完成模型集的切换。

2 基于Huber更新的鲁棒容积滤波方法

当量测噪声不再符合高斯分布时，若仍用EKF等滤波方法会导致跟踪滤波器的估计精度下降甚至发散，而Huber 滤波作为一种混合H1/H2的滤波方法，对非高斯噪声具有良好的鲁棒性。考虑到基于确定性采样的CKF 具有比EKF 更高的近似精度和良好的数值稳定性，本文将Huber 滤波与CKF 融合进行滤波器的设计。

2.1 广义极大似然估计

首先考虑如下的线性回归问题：

式中：H为量测矩阵；v为方差阵为R的量测噪声。利用量测噪声方差阵进行如下变换：

Huber 利用广义极大似然估计来求解（15）所示的线性回归问题，即计算如下指标函数的极小值：

对式（16）求导并令其等于0，可得：

通过定义权重函数ψ(δi)=及权重矩阵Ψ=diag(ψ(δi))，则其解的隐含数方程可表示为

Huber 通过选用如下混合l1和l2的ρ函数以获得对非高斯噪声的鲁棒性：

式中：γ为可调参数。Huber 滤波通过选取迭代初值：

并按下式迭代至收敛获取估计的结果。

2.2 容积Huber-based滤波

容积卡尔曼滤波作为一种确定性采样的非线性滤波方法，通过径向容积规则进行容积点的选取，并利用非线性方程对容积点进行传播，以此获得非线性系统的后验估计，其不仅具有比扩展卡尔曼更高的近似精度，而且相对于无迹卡尔曼来说其数值稳定性更强。考虑HGV 跟踪系统为非线性系统，因此使用容积卡尔曼滤波与Huber算法相结合，处理非线性系统中的非高斯噪声问题，考虑如下状态方程（即mk）已确定的非线性子模型系统，将(xk)简写为f(xk)，则式（1）和式（2）可记为

则基于Huber的容积滤波算法步骤如下：

1) 时间更新

式中：Sk-1为协方差矩阵Pk-1|k-1的Cholesky 分解。ξj为如下点集的第j列：

将容积点通过非线性状态方程进行传播，有：

2) 量测更新

生成用于量测更新的容积点：

定义状态预测误差为ek=xk-，并将量测方程线性化：

可构建如下线性回归问题：

取迭代初值为：

则迭代求解的状态估计值以及误差协方差为：

3 高超声速滑翔目标高精度跟踪方法

本节将建立HGV 运动模型集以及地基雷达的量测模型，随后基于有向图变结构多模型结构并利用容积Huber-based 滤波方法建立HGV 高精度跟踪滤波器。

3.1 高超声速滑翔目标运动模型集

HGV 在滑翔段常见的飞行方式包括平衡滑翔和跳跃滑翔，由于这两种飞行方式的弹道特性有明显不同，因此需要分别建立目标运动模型。

对于平衡滑翔运动阶段，其弹道变化相对平缓，可用“当前”统计模型对其进行描述，该模型假设目标当前的加速度在上一时刻的加速度邻域范围内。取目标的位置、速度以及加速度作为状态量，即：

则一维的“当前”统计模型离散化后的状态方程为

式中：α为机动频率参数，T为采样步长。噪声wk的方差为：

σ2代表“当前”加速度方差，满足：

其中，amax和a-max分别为最大正负加速度。

对于跳跃滑翔运动阶段，考虑高超声速滑翔目标在该阶段的加速度存在周期振荡的特点，可用正弦波模型对其进行描述。同时，由于气动力的存在，目标的加速度均值不为零且随时间变化，并且在阻力作用下飞行器的能量逐渐耗散，导致周期性逐渐减弱，因此，本文选取文献［10］所述的ANMDO模型对跳跃滑翔阶段进行建模。取目标的位置、速度、加速度和加加速度作为状态量，即：

则一维的ANMDO模型离散化后的状态方程为

式中：Fk为状态转移矩阵，满足

其中，

β代表权重系数；μ代表衰减系数；U为加速度补偿项，满足

式中：ω为振荡频率。当μ为零时，模型中的加速度仅表现周期性，无衰减；当ω为零时，加速度仅表现衰减性，无周期性。因此通过选择合适的衰减系数和振荡频率参数，可以保证角加速度同时具有周期性和衰减性。

机动频率α是“当前”统计模型的主要参数，为保证对平衡滑翔段的覆盖性，完备模型集中包含两个机动频率不同的“当前”统计模型，其模型参数分别为α1<α2。在ANMDO 模型中，振荡频率ω是其主要的模型参数，考虑跳跃滑翔阶段目标可能具有的不同振荡周期，完备模型集中包含3 个振荡频率不同的ANMDO 模型，对应的模型参数在目标可能的振荡频率变化范围内选取，即[ωmin<ω1<ω2<ω3<ωmax]，则完备模型集中模型组合的有向图网络为{α2，α1，ω1，ω2，ω3}，取实时模型集数量为3，则共完备模型集可分为3 个可能模型集，分别为M1={α2，α1，ω1}，M2={α1，ω1，ω2}，M3={ω1，ω2，ω3}，3 个可能模型集间的切换准则为：

1) 假设实时模型集为M1，若ω1对应的ANMDO模型在多模型算法中的模型概率最大且大于设定阈值λ，则下一时刻的实时模型集切换为可能模型集中的M2；否则下一时刻的实时模型集仍保持为M1；

2) 假设实时模型集为M2，若α1对应的“当前”统计模型在多模型算法中的模型概率最大且大于设定的阈值λ，则下一时刻的实时模型集切换为M1；若ω2对应的ANMDO模型的模型概率最大且大于设定阈值λ，则下一时刻的实时模型集切换为M3；否则，下一时刻的模型集保持不变；

3) 假设实时模型集为M3，若ω1对应的ANMDO的模型概率最大且大于阈值λ，则下一时刻的实时模型集切换为M2；否则，下一时刻的模型集不变。

3.2 地基雷达量测模型

地基雷达通过主动发射电磁波并接收回波对目标进行探测，具有探测精度高，作用距离远等优势，常用来对HGV 的滑翔段进行探测。地基雷达的量测信息包括目标相对于雷达站的斜距r、高低角γ及方位角η，即：

对应的量测方程为：

式中：Δx，Δy和Δz为HGV在雷达探测坐标系中的位置分量。

3.3 跟踪滤波器算法流程

将建立的HGV 目标运动模型作为状态方程，地基雷达量测模型作为量测方程，则基于有向图多模型结构和容积Huber-based 滤波算法的HGV 高精度跟踪算法流程可总结如下：

1) 数据输入交互：将上一时刻各子模型的按照式（4）至式（7）进行融合得到各子模型的模型概率和当前时刻各子模型的状态初值。

2) 状态滤波：各子模型按照容积Huber-based方法进行滤波，按照式（24）至式（42）得到各子模型的状态估计，估计误差协方差，以及用于模型更新的新息及其协方差。

3) 模型概率更新：利用获得的新息及其协方差，按照式（9）至式（10）更新当前时刻的各子模型的后验模型概率。

4) 融合输出：利用更新后的模型概率和各子模型状态估计及协方差，按式（12）至式（13）进行加权融合输出。

5) 模型集切换：根据后验模型概率利用有向图多模型的切换准则对实时模型集进行切换，确定新的当前实时模型集。

4 仿真校验

4.1 仿真场景

为验证本文所提的CHF-DSVSMM 算法在HGV跟踪中的性能，现以CAV-H 飞行器为例构建如下的仿真场景。设置飞行中最大过载3 倍重力加速度、最大热流密度1 000 kW/m2、最大动压300 kPa，仿真算例初值条件如表1所示。

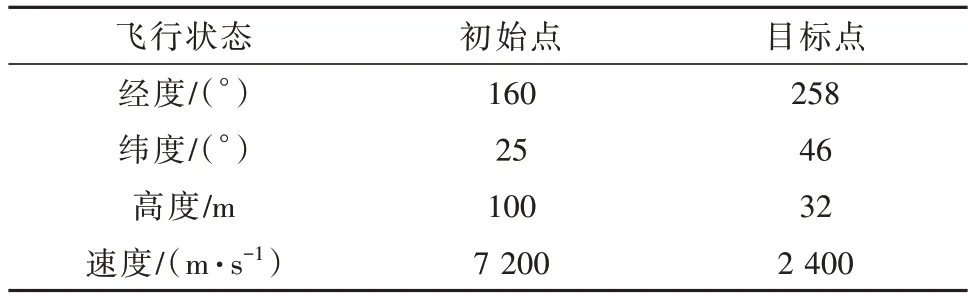
表1 飞行轨迹优化算例的初值Table 1 Initial value of flight trajectory optimization example

采用高斯伪谱方法进行轨迹优化［27］，HGV 飞行轨迹如图2 所示，目标飞行速度变化曲线如图3 所示。地基雷达部署位置经度、纬度、高度为[222.5°，40°，0 m ]，假设雷达最大可测量距离为750 km，将可探测弧段同时绘制于图2 中，采样频率10 Hz，测距精度σr=100 m，测角精度σρ=ση=0.1°。

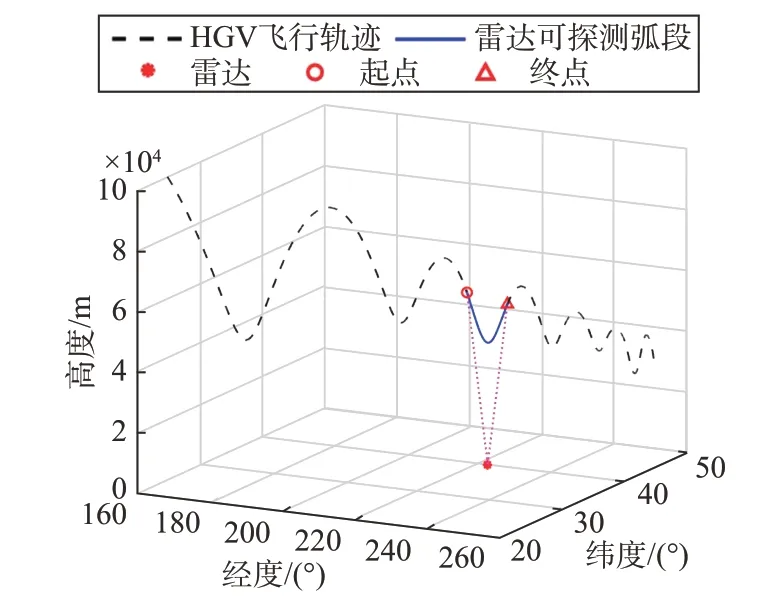
图2 HGV飞行轨迹及跟踪场景Fig.2 HGV flight trajectory and simulation scene

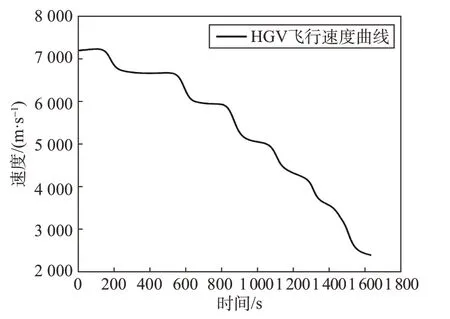
图3 速度变化曲线Fig.3 Target velocity

4.2 仿真一：高斯噪声条件下轨迹跟踪

在所建立的仿真条件下，利用CKF 并结合CSM单模型、文献［10］的ANMDO 模型、文献［13］的交互式多模型、文献［7］所提的自适应动力学模型（Adaptive dynamical model）以及本文所提的CHFDSVSMM 算法进行HGV 的轨迹跟踪，单模型ANMDO 模型中参数设置为权重系数β=0.7，衰减频率μ=11 000，周期频率ω=0.05；IMM 算法由Singer、CA、CT 三个模型构成，Singer 模型的机动频率为α=140；自适应动力学模型中具体参数见文献［7］；CHF-DSVSMM 的模型集为“当前”统计模型α1=160，α2=140 和ANMDO 模型ω1=0.07，ω2=0.05，ω3=0.03，切换阈值为λ=0.8。首先在高斯噪声条件下对验证所提算法对HGV 的跟踪精度，进行500 次蒙特卡洛仿真试验，仿真结果如图4至图6所示。

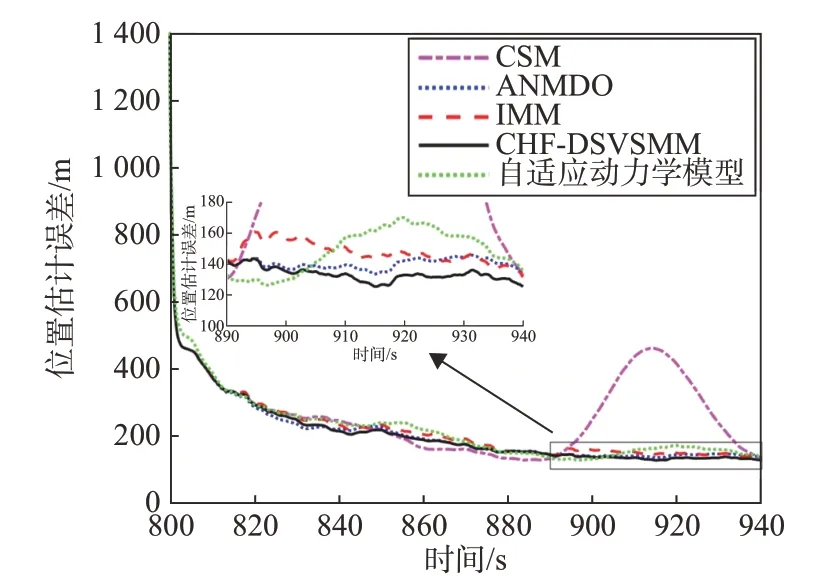
图4 位置估计误差Fig.4 Position estimation error of different filters

图5 速度估计误差Fig.5 Velocity estimation error of different filters

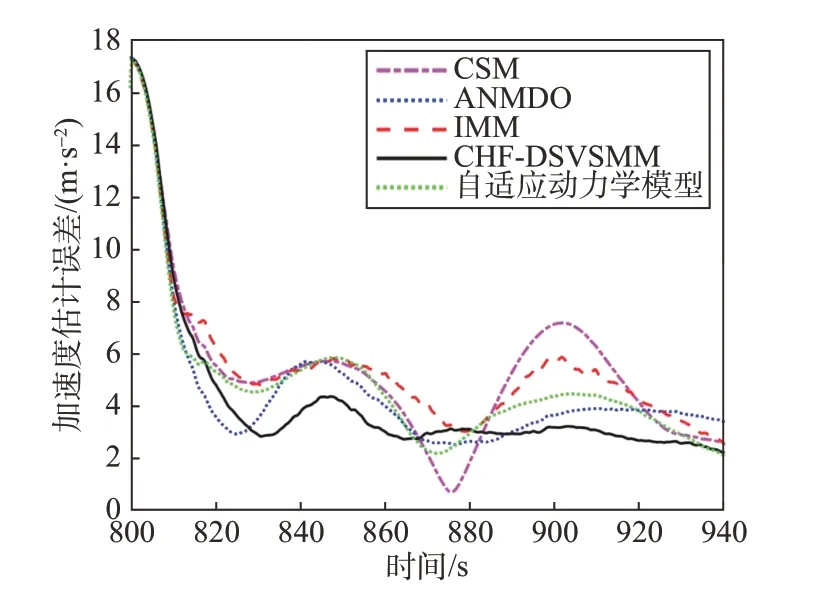
图6 加速度估计误差Fig.6 Acceleration estimation error of different filters

根据仿真结果可知，由于CSM 单模型和文献［13］中IMM 所包含的模型均难以适应HGV 在跳跃滑翔时的强机动特性，因此跟踪精度最差。ANMDO单模型同时具有周期性和衰减性，因此可对跳跃滑翔运动实现较为准确的跟踪，但单模型方法下其模型参数固定，不能实时准确地适应HGV 真实的机动情况，导致其跟踪精度难以长时间保证。自适应动力学模型需要对加速度进行自适应估计，因此需要得到一定数据量后才能对加速度变化进行响应。而本文通过建立包含多种参数的CSM 和ANMDO的模型集，实现了对HGV 跳跃滑翔运动较为完整地覆盖，并通过有向图切换的方法在模型集中自适应地快速调整实时模型集，在保证了计算量的同时实现了对HGV 跳跃滑翔阶段持续稳定地高精度跟踪。

4.3 仿真二：非高斯噪声条件下轨迹跟踪

为进一步验证所提算法对非高斯噪声的鲁棒性，假设地基雷达受到等离子鞘套的干扰，表现出的非高斯探测噪声满足闪烁噪声形式：

进行500 次独立的蒙特卡洛打靶试验，仿真结果如图7至图9所示。

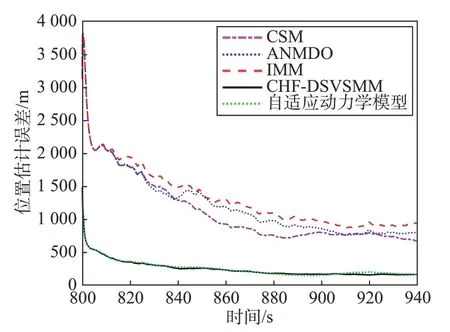
图7 位置估计误差Fig.7 Position estimation error of different filters

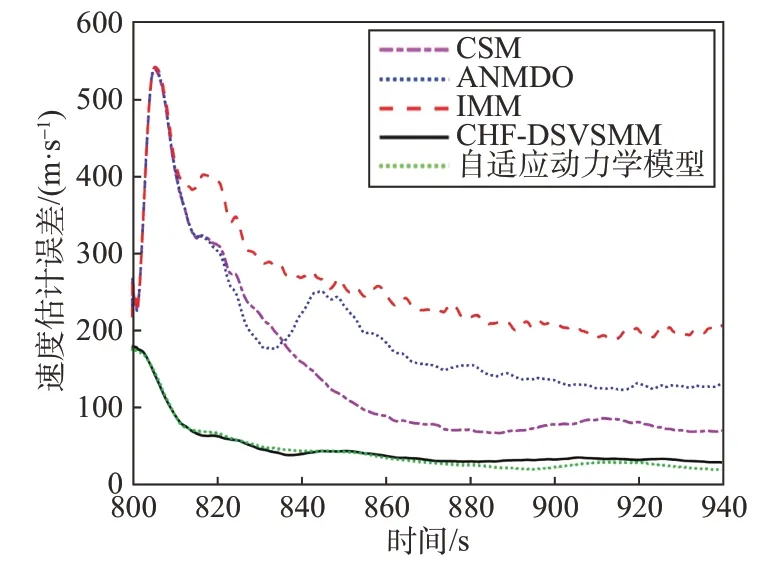
图8 速度估计误差Fig.8 Velocity estimation error of different filters

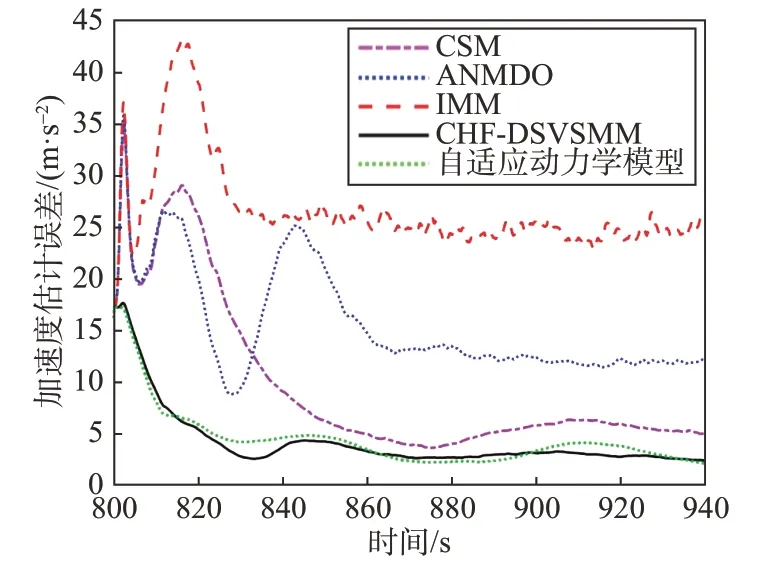
图9 加速度估计误差Fig.9 Acceleration estimation error of different filters

定义平均均方根误差（ARMSE）作为性能指标，即：

式中：N为蒙特卡洛打靶次数；M为仿真步长；Xk和分别为状态真值与估计值。

将两种仿真情况下不同算法的ARMSE 总结如表2。

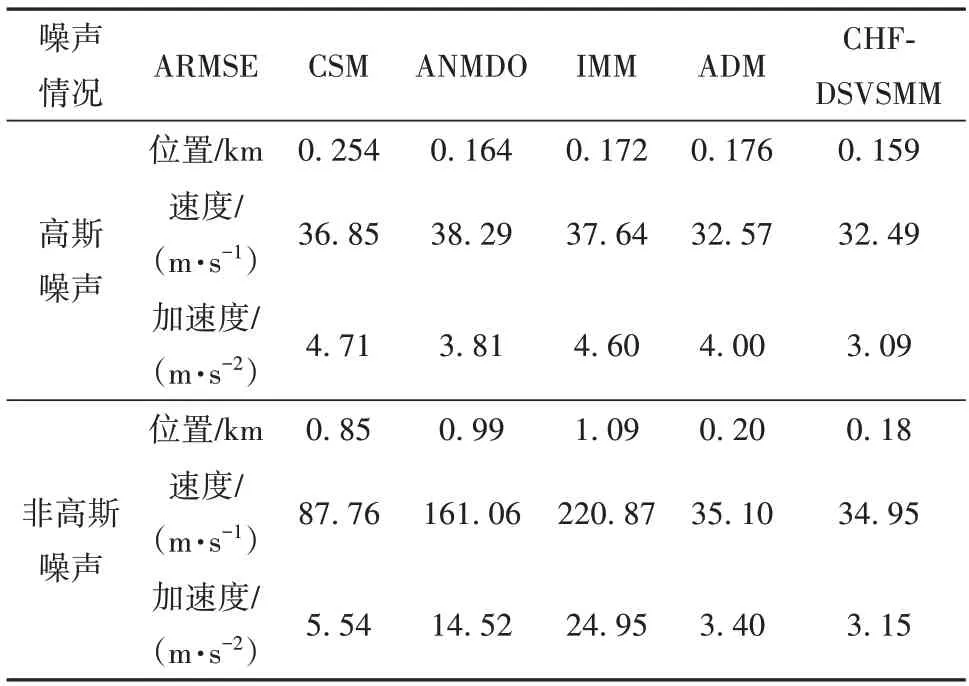
表2 不同算法估计结果的ARMSETable 2 ARMSE of different filters

根据仿真结果可知，在非高斯噪声条件下，单模型和IMM 中采用的CKF 估计精度明显下降，而由于文献［7］和本文均采用了HCF 处理量测过程中出现的非高斯噪声，其跟踪精度在非高斯噪声条件下精度相当。因此所提HCF-DSVSMM 方法不仅可以在高斯噪声条件下取得稳定的跟踪效果，而且对非高斯噪声具有良好的鲁棒性，非高斯噪声对所提算法影响最小。

5 结论

本文研究了非高斯噪声条件下的临近空间HGV 轨迹跟踪方法，通过将容积Huber-based 滤波方法与有向图变结构多模型方法相结合，提出了CHF-DSVSMM 算法，并设计了HGV 目标运动模型集。与其他方法相比，本文所建立的模型集可以更为准确地描述HGV 跳跃滑翔阶段的运动，并且利用有向图切换的方法在保证计算量的同时实现了对HGV 的稳定高精度跟踪，同时，算法中的HCF 还提供了对非高斯噪声的鲁棒性。仿真结果验证了该算法的有效性，仿真结果表明，所提算法可以实现对具有多种运动情况的HGV 持续稳定的高精度跟踪，算法通过模型集切换的方式自适应的改变目标运动模型集，达到了对HGV 实时运动特性的准确描述，且当存在非高斯量测噪声时，算法仍保持了良好的鲁棒性和跟踪精度。