弹性飞行器飞行动力学建模与刚柔耦合阶次分析

安 阳，王天舒

（清华大学航天航空学院，北京 100084）

0 引言

随着飞行器飞行速度的提高、结构尺寸的增大以及结构重量的降低，柔性结构在飞行器整体结构中的占比越来越大［1-3］，弹性振动对飞行器动力学与控制的影响也随之增强［4-6］。例如，高超声速飞行器为了满足高速和大射程的要求，一般具有较大的长细比和较轻的结构重量，导致其本体弹性模态的固有频率较低，表现出明显的柔性特性［7-8］。空间站太阳能电池阵列等大型网架式空间结构由于含有杆、板、绳索等柔性构件以及它们之间的非线性约束［9］，不再符合传统柔性航天器模型中具有中心刚体平台、柔性结构仅在附件中存在的假设［10］。此外，近年来提出的太阳帆航天器［11］、空间太阳能电站［12］等新概念航天器，大型柔性结构也占其整体的绝大部分。针对弹性飞行器的动力学建模及模型降阶问题，国内外学者已进行了大量研究［13-17］。杨辉等［18］指出了混合坐标法的不足，并基于Hamilton 变分原理和有限元法导出了刚柔耦合系统一次近似的动力学模型，该模型充分考虑了中心刚体大范围运动与柔性附件弹性振动的耦合效应。郭东等［19］基于一种瞬态坐标系，通过拉格朗日方程和有限元法，推导了能够描述弹性飞行器结构、流场与控制等多学科耦合特性的动力学模型。Cao等［20］基于哈密顿原理建立了具有侧向太阳电池阵的三轴稳定航天器的刚柔耦合动力学模型，采用全局模态法求解了模型的固有频率和全局模态振型，并通过与有限元软件的结果对比，说明了该方法可以准确描述航天器的刚柔耦合运动。袁秋帆等［21］通过定义广义全局模态振型，基于哈密顿原理推导了一种单翼大挠性航天器的全局模态动力学模型，并采用瑞利瑞兹法得到了非约束模态频率和振型的计算方法。闫玉龙等［22］基于D’Alembert 原理推导了航天器柔性附件的振动方程，通过准坐标Lagrange 方程建立了刚-柔-晃耦合的航天器状态方程，并指出柔性附件的安装位置对于航天器的动力学特性具有重要影响。张恒浩等［23］基于正交理论建立了挠性航天器刚柔耦合系统的离散动力学模型，阐明了动力学刚化现象产生的原因和对航天器产生干扰的干扰源，并提出了一种能够抑制这种干扰的一阶动力学模型。曹芊等［24］采用李群SE（3）上的指数坐标描述了航天器的位置与姿态，在SE（3）框架下推导了柔性航天器姿-轨-结构一体化的动力学模型，进而得到了其相对动力学模型。Huang等［25］采用有限元法建立了柔性桁架两端附着刚体类航天器的动力学模型，通过分析得到了柔性航天器的无约束模态。朱尊红等［26］提出了一种自旋挠性航天器帆板的梁式简化模型，基于欧拉方程和哈密顿原理建立了航天器的动力学方程，并解释了刚性模态和弹性模态之间的耦合。Kim等［27］将一种基于单元连通性的刚度评估方法与绝对节点坐标法相结合，提出了一种基于刚度评估的柔性多体系统动力学模型降阶方法，提高了传统建模方法的计算效率。

在目前的弹性飞行器动力学建模领域，对描述弹性体变形运动的变形场阶次和模态截断阶次等问题已有较多研究［18，28-29］，而对在模态阶数与弹性变形场阶次选定后，在动力学模型推导过程中产生的各阶弹性变形相关项取舍问题的研究较少。在传统的中心刚体-柔性附件模型中，中心刚体的质量、转动惯量等在飞行器整体中占有绝对优势，柔性附件的弹性振动对飞行器整体动力学的影响较小，因此通常忽略动力学模型推导过程中产生的关于弹性变形的高阶项，而近似后的模型仍能保有满足工程要求的精度。但当飞行器主体呈现柔性特性时，这种高阶项是否还能忽略及其对整体动力学的影响尚无定论。此外，在动力学模型建立后，通常选用无外力作用时系统的线动量和角动量作为守恒量，检验模型的正确性和对比模型的计算精度。系统动量表达式中弹性变形相关项的保留阶次也可能对其计算结果的准确性产生影响。研究弹性变形相关项的保留程度对飞行器动力学及动量计算的影响，对动力学模型的降阶与验证具有重要的指导意义。本文首先基于虚功率原理与混合坐标法建立弹性飞行器的飞行动力学模型，并定义刚柔耦合阶次以描述动力学模型推导过程中产生的弹性变形相关项的保留程度，然后以由柔性中心体和刚性附件组成的刚柔耦合系统为例，对比分析动力学模型及动量公式的刚柔耦合阶次对动力学响应与守恒量的影响。

1 基于虚功率原理的弹性飞行器动力学建模

假设飞行器本体为弹性体，舵面为刚体，二者通过单自由度旋转副连接。飞行器系统的构型及坐标系定义示意图如图1 所示。其中，惯性系Oxyz固定在地面，本体系Ocxcyczc为与本体固连的浮动坐标系，第i(i=1，…，np)个舵面的随体系Op，ixp，iyp，izp，i与舵面固连且原点位于舵面与本体的连接处。

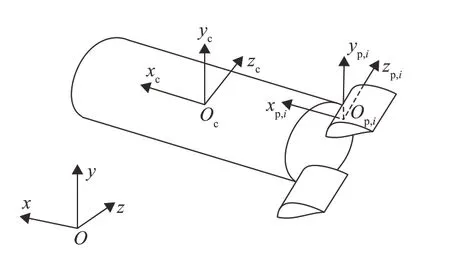
图1 飞行器系统构型与坐标系定义示意图Fig.1 Configuration of the flight vehicle system and coordinate system definition diagram

虚功率原理的表达式为：

式中：δPI为惯性力虚功率，δPa为主动力虚功率，δPe为虚应变能变化率，δPd为阻尼力虚功率，符号Σ 表示对系统求和。

基于虚功率原理推导弹性飞行器飞行动力学方程的主要步骤为：首先，计算飞行器本体与舵面等附件的速度、加速度与速度变分；然后，计算本体及各附件的虚功率；最后，将各部件虚功率代入虚功率原理的表达式，根据各变分相互独立得到飞行器的动力学方程。

采用有限元法将飞行器本体离散为l个质量单元，则本体上第k(k=1，…，l)个质量单元相对惯性系原点的矢径为：

式中：Rc为本体系原点相对惯性系原点的矢径，表示飞行器的平动位移为本体未发生变形时，其第k个质量单元相对本体系原点的矢径为本体第k个质量单元的弹性变形矢量，利用模态展开法表示为：

式中：rcp，0为本体未发生变形时舵面系原点相对本体系原点的矢径；rp为舵面上任一质量单元相对舵面系原点的矢径。式（5）体现了本体弹性振动对舵面运动的影响，以下记rcp=rcp，0+

基于式（2）与式（5）计算飞行器本体及舵面的速度、加速度、速度变分与虚功率，代入式（1）并根据变分、δωc、相互独立，可得：

飞行器平动动力学方程为：

式中：m为飞行器的总质量；S为飞行器相对本体系的总静矩；ωc为本体相对惯性系的转动角速度，即飞行器的姿态角速度；F为飞行器主动力的合力；Qt为飞行器平动耦合惯性力的合力；耦合系数阵Ct的表达式为：

式中：Cct为本体弹性振动对飞行器平动的耦合系数阵；Crt，i为第i个舵面受本体振动影响而产生的对飞行器平动的附加耦合系数阵；mc，k为本体上第k个质量单元的质量；mp，i为第i个舵面的质量；np为舵面的数量。

飞行器姿态动力学方程为：

式中：J为飞行器相对本体系的总惯量张量；T为飞行器主动力矩的合力矩；Qr为飞行器转动耦合惯性力的合力；耦合系数阵Cr的表达式为：

式中：rpp，i为第i个舵面的质心相对其随体系原点的矢径；Ccr为本体弹性振动对飞行器转动的耦合系数阵；Crr，i为第i个舵面受本体振动影响而产生的对飞行器转动的附加耦合系数阵。需要说明的是：为了方便表示，在式（9）中仍使用了空间矢量的叉乘符号来描述位置矢量与模态矢量阵之间的运算关系。它表示将位置矢量分别与模态矢量阵中的各阶模态矢量进行矢量叉乘，再将叉乘得到的结果矢量按顺序排列成一行，得到一个新的矢量阵。

飞行器振动动力学方程为：

式中：Cc为飞行器本体的模态阻尼阵，Kc为模态刚度阵；Ff为飞行器的模态力；Qf为飞行器振动耦合惯性力的合力；模态质量阵Mf的表达式为：

式中：Mcf为飞行器本体的模态质量阵，当本体的模态矢量阵采用模态质量规一时，Mcf近似为单位阵；它是第i个舵面受本体振动影响而产生的附加模态质量阵，一般不是对角阵。则矩阵Mf的非对角线位置也将出现非零元素，使方程（10）中经主坐标变换后的广义坐标也不再完全解耦。

飞行器的线动量表达式为：

式中：mc为飞行器本体的质量；Sc为飞行器本体相对本体系的静矩，Sp，i为第i个舵面相对舵面系的静矩；ωp，i为第i个舵面相对本体的转动角速度。

飞行器的角动量表达式为：

式中：pc为飞行器本体的线动量，pp，i为第i个舵面的线动量；Jc为飞行器本体相对本体系的惯量张量，Jp，i为第i个舵面相对舵面系的惯量张量。

为了检验所建立的动力学模型的正确性，采用MATLAB 语言编写其仿真程序，并与ADAMS 软件进行仿真结果对比。当本体与舵面均不受外力作用，仅对两者的相对转角施加驱动使其按照正弦规律变化时，自编程序与ADAMS 软件的部分仿真结果对比如图2 所示。图中两组曲线吻合较好，验证了动力学模型及其仿真程序的正确性。

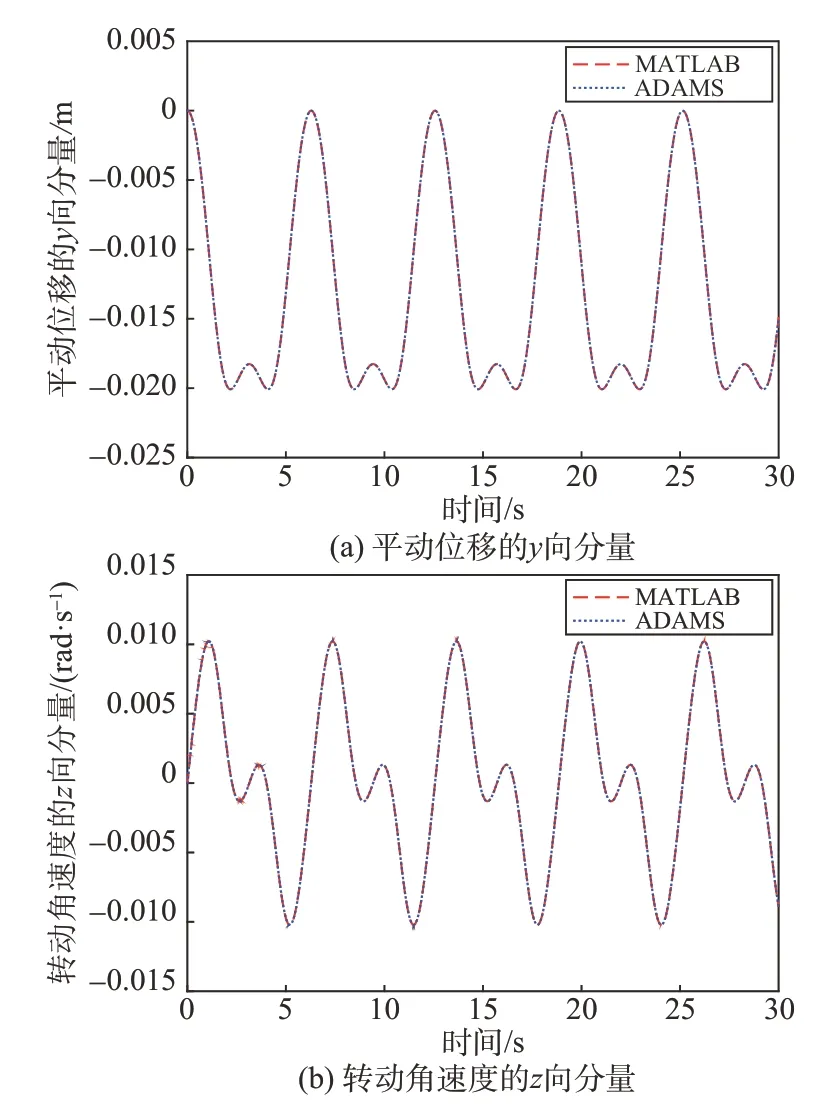
图2 自编程序与ADAMS的仿真结果对比Fig.2 Comparison of simulation results between self-programmed program and ADAMS

2 刚柔耦合阶次的定义

上文推导的动力学模型是未忽略各阶弹性变形相关项的完整模型，其动力学方程与系统角动量表达式中含有模态坐标的一阶与二阶项，将此动力学模型定义为二次刚柔耦合模型，动量公式定义为二次动量公式。在二次模型中，本体与舵面相对本体系的静矩、线动量、平动与振动耦合惯性力、本体振动对飞行器转动的耦合系数、舵面对飞行器转动的附加耦合系数中含有模态坐标的一阶项，本体与舵面相对本体系的惯量张量、角动量、转动耦合惯性力中含有模态坐标的一阶与二阶项。如飞行器本体相对本体系x轴的转动惯量Jc，xx、本体的转动耦合惯性力Qcr的表达式分别为：

在实际的工程应用中，为了简化模型和减少计算量，计算本体及舵面的速度、加速度与速度变分时通常根据弹性变形为小量而将模态坐标项忽略，只保留模态坐标的导数项。简化后本体与舵面上任一质量单元相对惯性系的速度、加速度与速度变分分别为：

基于式（16）与式（17）推导的动力学模型中，惯性参数、弹性耦合系数、耦合惯性力与动量计算公式中均不含模态坐标项，将此动力学模型定义为零次刚柔耦合模型，动量公式定义为零次动量公式。如转动惯量Jc，xx在此只保留式（14）中的第一项，耦合惯性力Qcr的表达式则简化为：

在二次刚柔耦合模型的基础上，忽略模态坐标的二阶项而只保留一阶项，将这样简化后的动力学模型定义为一次刚柔耦合模型，相应的动量公式定义为一次动量公式。如转动惯量Jc，xx在此只保留式（14）中的前两项。而对于耦合惯性力Qcr，由于式（15）仅在惯量张量Jc中含有模态坐标的二阶项，故一次与二次模型中的Qcr仅存在惯量张量保留阶次的不同。在这里，考虑到飞行器弹性振动的振幅虽然较小，但振动速度较快，模态坐标的一阶导数的数量级高于模态坐标，故在一次模型中未将模态坐标与模态坐标的一阶导数的乘积项作为高阶小量忽略，在零次模型中也未将模态坐标的一阶导数的一阶项忽略。

3 模型刚柔耦合阶次对动力学分析的影响

在本体振动的基频f0=9.9 Hz，系统不受外力，舵面与本体间的相对转角按αp=cost-1（t表示时间）规律变化的条件下，各次刚柔耦合模型动力学时域响应的部分结果对比如图3所示。

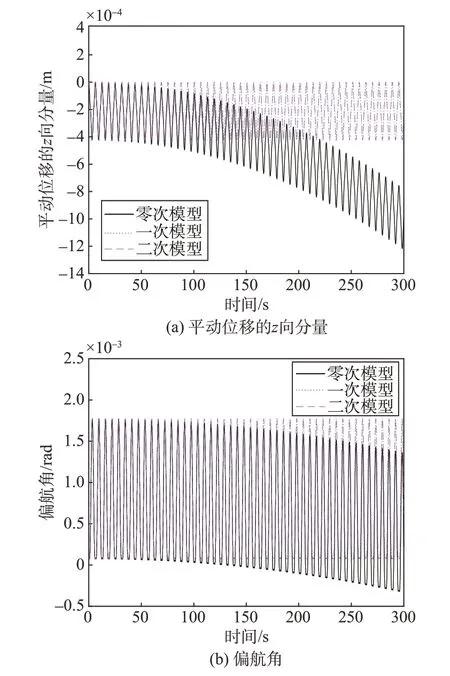
图3 各次刚柔耦合模型的时域响应对比Fig.3 Comparison of time domain response of rigid-flexible coupling models of each order

一次模型与二次模型的时域响应基本吻合，而零次模型的时域响应随着时间的增长逐渐与一二次模型的结果出现偏差，绝对值较小的响应值的偏差较为显著。考虑到系统不受外力，本体与舵面间的相对转角按正弦规律驱动，故理论上动力学时域响应值应在一固定的平衡位置上周期性变化，不会呈现出发散的变化趋势，所以零次模型的长时间计算结果是不合理的。

在没有外力作用且初始速度为零时，飞行器总的线动量和角动量的计算值都接近理论值0，则认为动力学模型是合理的，计算值的绝对值越小，则认为模型的计算精度越高。为了比较动力学模型的刚柔耦合阶次对系统动量计算结果的影响，本节中线动量与角动量的计算均使用二次动量公式。各次刚柔耦合模型的线动量与角动量计算结果对比如图4 所示，各次模型的线动量与角动量计算结果均接近0，二次模型计算结果的量级最低，可以认为其计算精度最高。

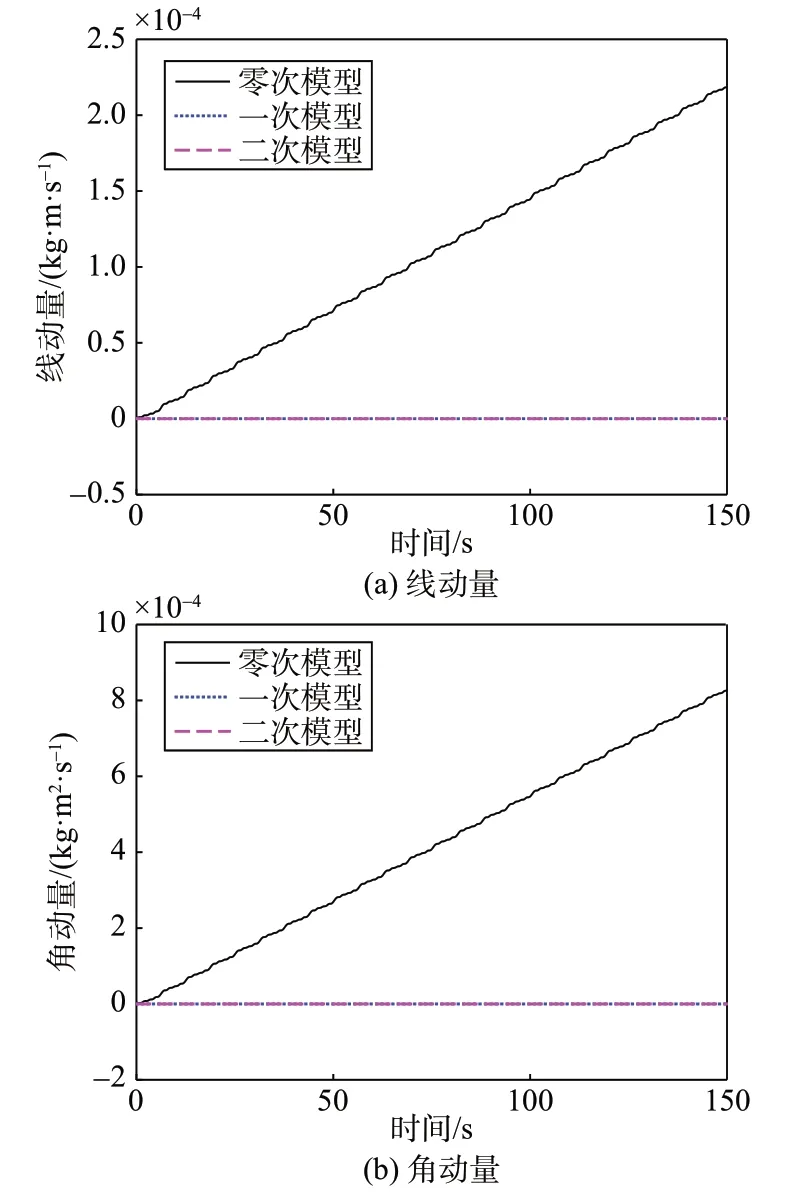
图4 各次刚柔耦合模型的动量对比Fig.4 Comparison of linear momentum and angular momentum of rigid-flexible coupling models of each order

零次模型的线动量与角动量计算结果比一、二次模型的高6～10 个数量级，且随着时间的增长总体上呈近似线性地单调增大，该误差并非由数值积分过程引入，而是模型建立时在式（16）和式（17）中忽略了部分弹性变形相关项导致的。仅将一次和二次模型的动量计算结果进行对比，如图5所示。

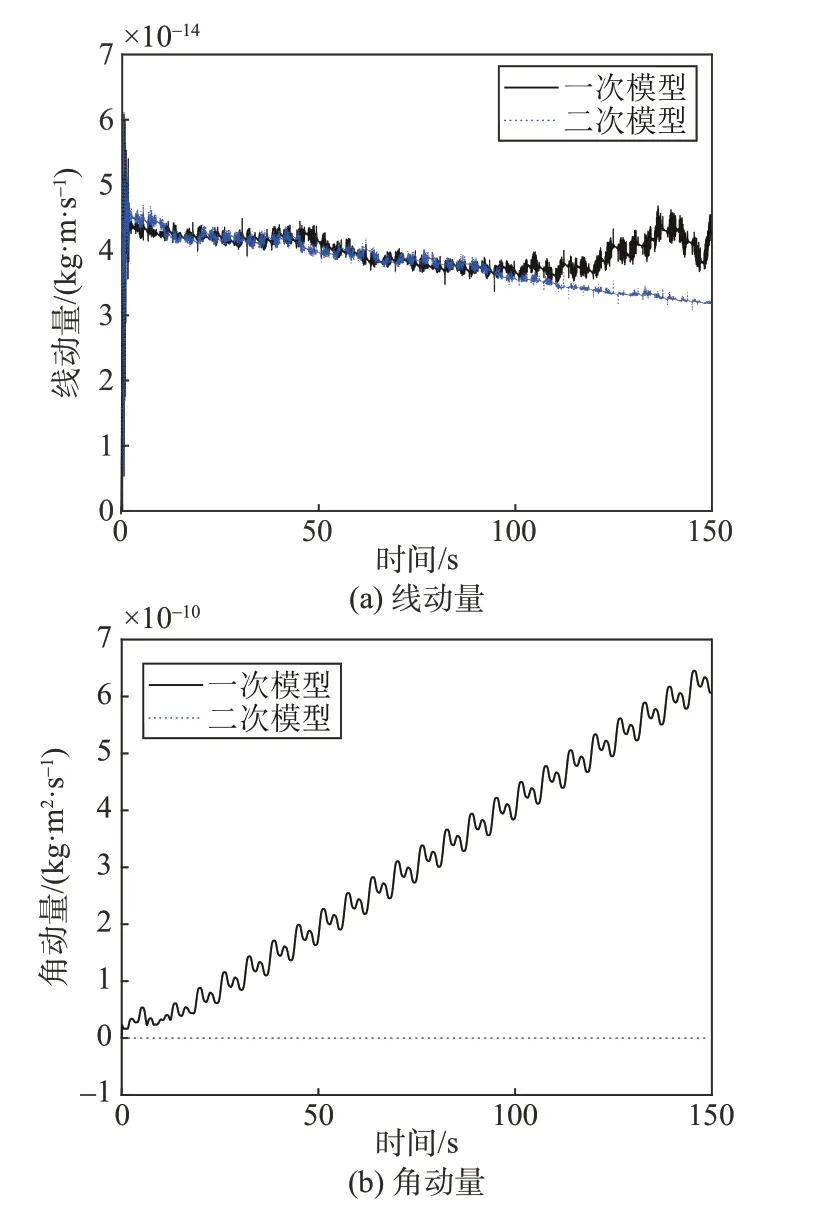
图5 一、二次刚柔耦合模型的动量对比Fig.5 Comparison of linear momentum and angular momentum of one-order and two-order rigid-flexible coupling models

一次模型的角动量计算结果比二次模型的高3 个数量级，且随着时间的增长总体上呈近似线性地单调增大，而两者线动量的计算结果较为接近。可以得出：系统角动量的计算精度对模型刚柔耦合阶次的变化比线动量更敏感。

为了分析刚柔耦合阶次对动力学分析的影响与中心柔性体振动频率的关系，将本体有限元模型的材料弹性模量改为原来的1/100，其他条件保持不变，本体振动的基频变为f′0=0.99 Hz。本体基频降低后的各次模型动力学时域响应的部分结果对比如图6所示。

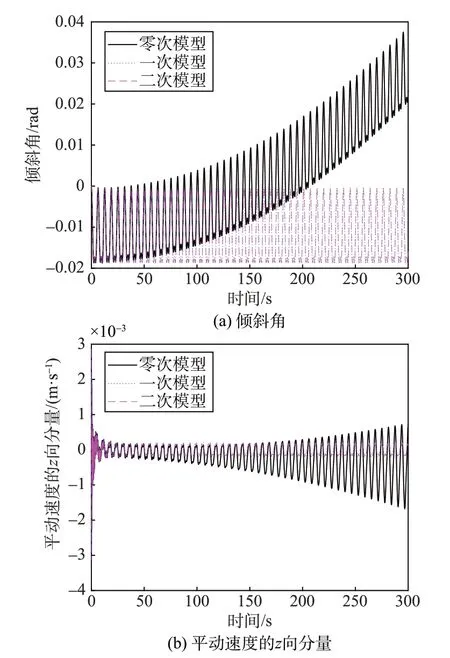
图6 本体基频降低后的时域响应对比Fig.6 Comparison of time domain response after the fundamental frequency reduction of the body

与本体振动基频为9.9 Hz 时的动力学时域响应结果对比，基频降低后零次模型与高次模型的计算结果偏差显著增大。此外，零次模型的计算结果中平动位移、欧拉角等位移量与高次模型的偏差比平动速度、角速度等速度量的偏差更明显。可以得出：刚柔耦合阶次对动力学分析的影响受中心柔性体振动频率的影响，中心柔性体振动的基频越低，零次模型动力学时域响应的结果与高次模型的偏差越大，计算误差越大。

本体基频降低前后零次模型的线动量与角动量、一次模型的角动量计算结果对比如图7所示。

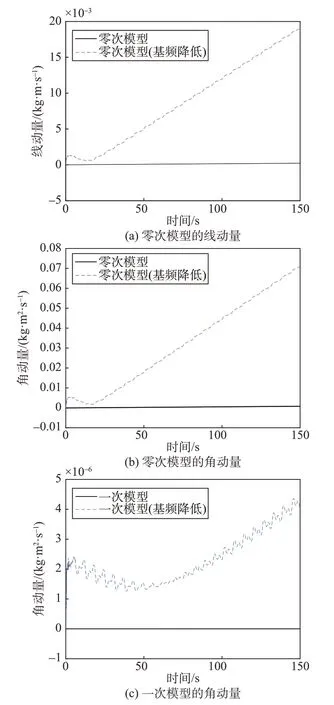
图7 本体基频降低前后的动量对比Fig.7 Comparison of linear momentum and angular momentum before and after the fundamental frequency reduction of the body

本体振动基频降低后，一次模型的角动量增大4个数量级，零次模型的线动量与角动量增大2个数量级。可以得出：中心柔性体振动频率降低会使由于模型刚柔耦合阶次降低而导致的线动量与角动量的计算误差增大。

4 动量公式刚柔耦合阶次对动量计算的影响

与本体振动基频f0=9.9 Hz 时的条件保持相同，采用各次动量公式计算零次刚柔耦合模型的线动量与角动量的结果对比如图8所示。

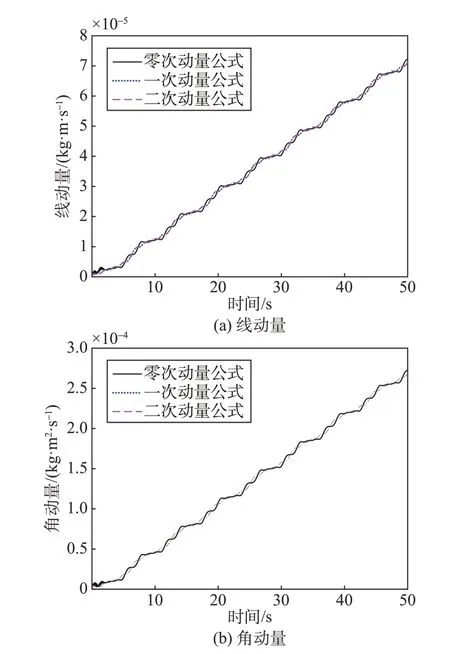
图8 零次刚柔耦合模型的各次动量对比Fig.8 Comparison of linear momentum and angular momentum of each order of zero-order rigid-flexible coupling model

各次动量公式计算所得的零次模型的线动量与角动量分别在同一个数量级。同样可以验证，采用二次动量公式计算一次模型的线动量与角动量，其结果与一次动量公式的计算结果在同一个数量级。可以得出：当动力学模型的刚柔耦合阶次较低时，采用较高阶次的动量公式并不能使线动量与角动量的计算精度提高。

采用各次动量公式计算二次刚柔耦合模型的线动量与角动量的结果对比如图9所示，仅将其中的一次和二次动量公式的计算结果进行对比如图10所示。

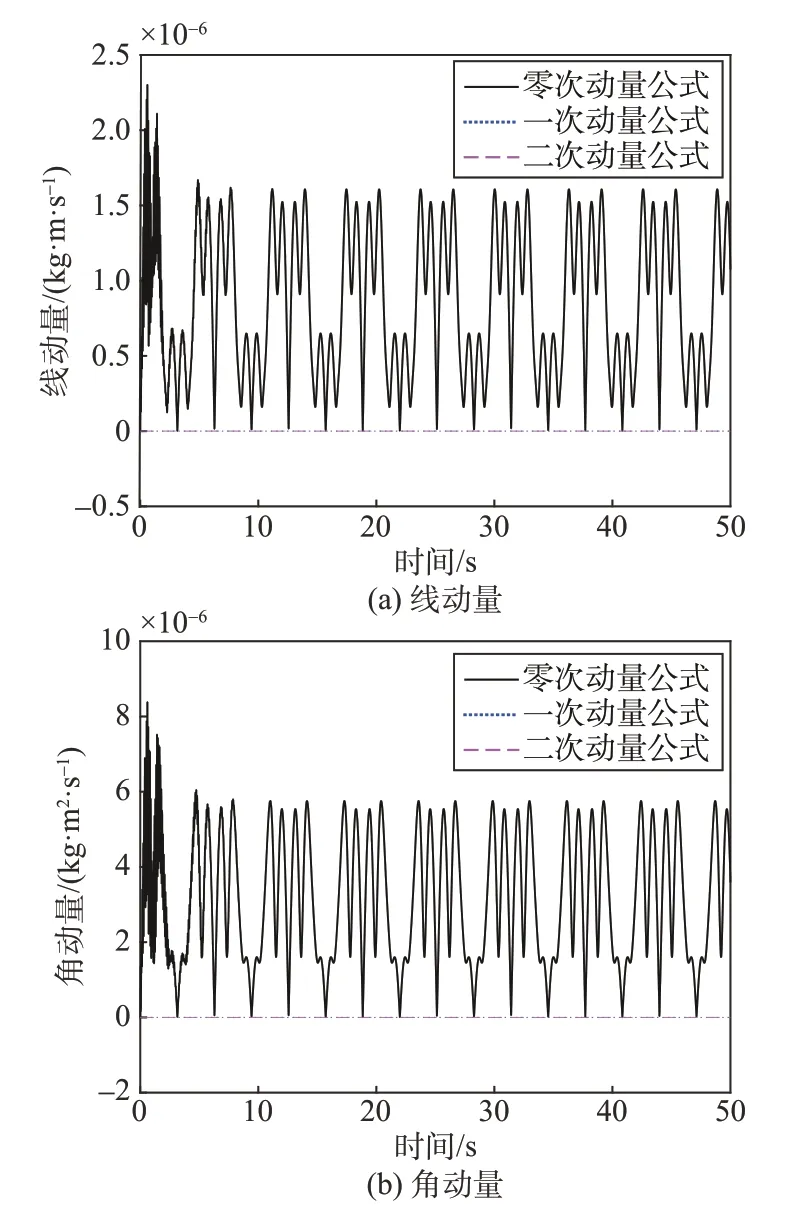
图9 二次刚柔耦合模型的各次动量对比Fig.9 Comparison of linear momentum and angular momentum of each order of two-order rigid-flexible coupling model

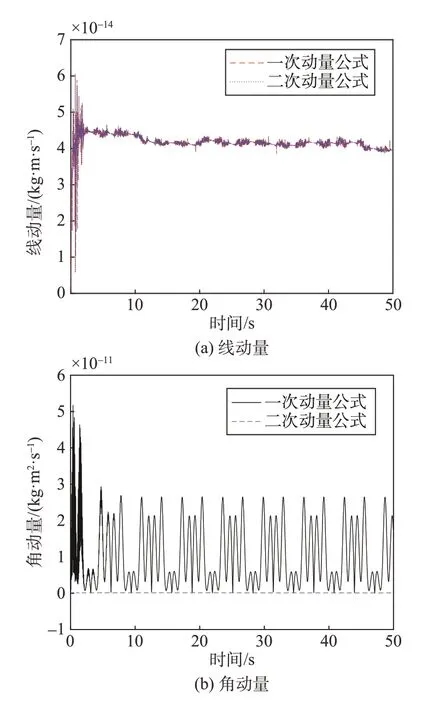
图10 二次刚柔耦合模型的一、二次动量对比Fig.10 Comparison of the one-order and two-order linear momentum and angular momentum of two-order rigid-flexiblecoupling model

采用零次动量公式计算二次模型的线动量与角动量，结果比二次动量公式的高8 个数量级。采用一次动量公式计算二次模型的角动量，结果比二次动量公式的高2个数量级。由于线动量的计算公式中不含模态坐标的二阶项，一次与二次线动量计算公式相同，故采用一次与二次动量公式计算的二次模型的线动量结果相同。同样可以验证，采用零次动量公式计算一次模型的线动量与角动量，其结果的数量级也比高次动量公式的计算结果高。可以得出：除一次与二次动量公式计算各次模型线动量的精度相同外，采用刚柔耦合阶次较低的动量公式计算阶次较高模型的线动量与角动量，误差将比高次动量公式的大。

5 结论

本文研究了弹性飞行器飞行动力学建模的问题，提出了飞行器的弹性耦合系数和广义模态质量的修正方法，可以精确描述连接在柔性本体上的部件对飞行器动力学的影响。分析了刚柔耦合阶次对计算精度的影响，发现随着刚柔耦合阶次的降低，动力学模型的时域响应和动量计算结果的误差可能会增大，且中心柔性体振动的基频越低误差越显著。进一步指出了在利用动量守恒检验系统的计算精度时，动量计算公式的刚柔耦合阶次应不低于动力学模型的刚柔耦合阶次。