一种小型火工机构的输出计算及其验证

杜永刚，王雪松，刘轶鑫，康昌玺，雷小光，张文台，孙永壮

（中国空间技术研究院兰州空间技术物理研究所，兰州 730000）

0 引言

折叠翼的展开技术是现代导弹结构系统的关键技术，该技术通过折叠翼面至弹体表面或其内部以减少导弹的外形包络空间，当脱离导弹发射箱或其内埋结构，导弹再展开、锁定其折叠翼面，并使其进入正常飞行状态，此外，潜射导弹的翼面在运载器中为折叠状态，当导弹与运载器分离后再展开翼面［1］。国内外的研究者开发了不同类型的折叠翼展开机构，大部分的弹翼被折叠在弹体表面，如美国的AGM-158 系列超音速导弹的翼面旋转折叠在弹体的表面，并按与弹体轴向平行的轴旋转展开［2］，因翼面处于弹体的外表面，该结构会影响弹体的气动外形。

为降低气动外形的影响，美国研究了一种直动式翼展机构，其收拢的翼面藏于弹体内部，并由推出机构将翼面推出弹体并锁定其位置［3］。南京航空航天大学研究了一种直动式翼展机构［4］，其翼面的初始状态是收缩于翼面收拢舱内，压缩弹簧将翼面沿直线推出，推出到位的翼面由限位轴销锁定。哈尔滨工业大学也开展了这种直动式翼面展开机构的研究［5］，该机构由解锁组件、推出组件、间隙消除组件组成，其翼面的推出组件为曲柄滑块机构，曲柄上安装有弹性驱动元件，其解锁及间隙消除组件均为记忆合金作动器。直动式翼展机构解决了上述气动外形的问题，但需设置翼的收拢舱段，该结构增加了导弹的长度。目前的导弹仍广泛采用折叠翼面至弹体表面的技术，展开机构的小型化是其重要的研究内容。

目前折叠翼的展开机构采用的主要动力装置为弹性蓄能器件和火工品。采用弹性蓄能器件的展开机构是在折叠翼面内安装并列圆柱弹簧，弹簧拉动滑轮组件展开翼面［6-7］，也有部分折叠翼面采用扭簧旋转展开翼面，如“游隼”无人机折叠翼的第二展开机构采用扭转弹簧［8］，还有一种以记忆合金丝驱动的导弹翼面折叠展开机构［9］，但这种技术没有工程应用的报道。因火工品的大输出力和小体积的优点，其在翼展机构中的应用受到了学者的广泛研究。早期的应用是火药燃气直接驱动活塞的翼展机构［10］，其巨大的冲击力将导致结构损坏，而火工品在翼展机构中的安全性和离散性不容忽视［11-13］，有研究通过优化火药形状或改变激发火药燃烧的方式延长火工品的工作时间，该研究降低了火工品对翼面的冲击［14］，也有研究报道了一种采用液体阻尼的火工作动器［15］，此外，中北大学在翼的展开结合处安装了缓冲橡胶以解决冲击问题［16］。目前比较先进的火工作动器采用了一种小孔阻尼技术，该作动器能形成自调节阻尼性能，其早期的输出计算采用了流-固耦合技术［17］，因这种研究方法的计算量过大，当前学者开始采用基于内弹道理论的数值计算方法。

旨在解决某翼展机构的小型化难题，本文开展了一种小型火工机构的研究。结合内弹道理论，提出了该火工机构的输出理论模型，通过仿真和大量试验结果的对比，证明该火工机构可解决薄形翼展机构的难题。

1 结构描述

该火工机构是一个由火工作动器驱动的旋转机构，再由旋转机构驱动载荷，该旋转机构是一种螺旋传动机构［18-19］，其最早应用在美国先进战略空射超音速导弹（ASALM）的翼展机构中［20］，其结构组成如图1 所示。为进一步减小体积，本文利用环形流道减小了火工作动器的体积［21］，图2 是该作动器的外观及工作原理，燃气由火药的燃烧腔体进入各腔体，活塞杆则在高压燃气的作用下输出推力和位移，燃气流速决定了活塞的运动速度。

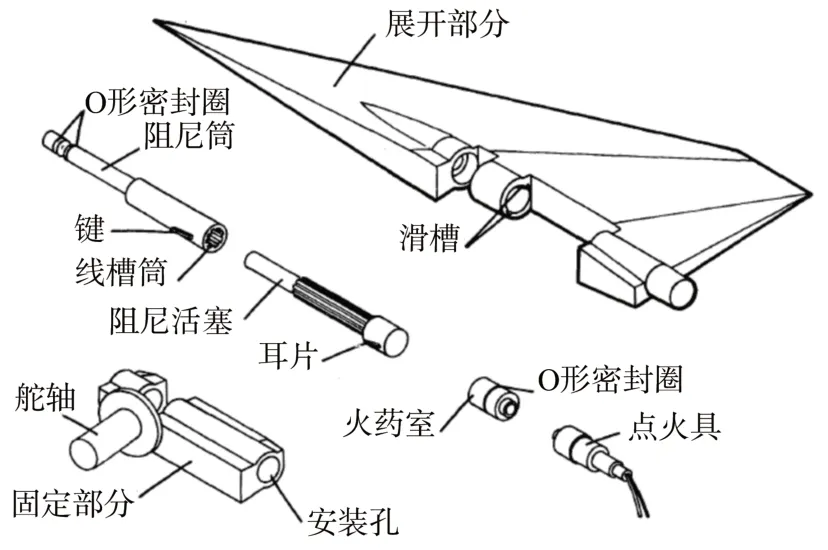
图1 美国ASALM的展开机构Fig.1 Unfolding mechanism of ASALM

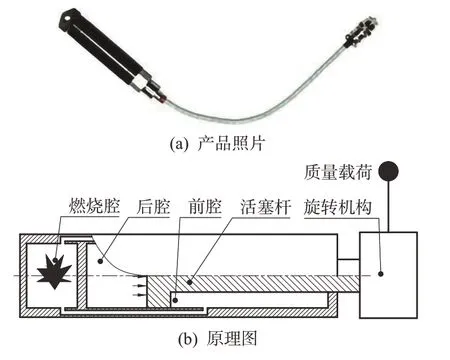
图2 小型火工作动器Fig.2 A small explosive actuator

根据上述的机构组成及其原理，可知该机构的理论模型是由火工作动器的内弹道动力学和螺旋传动动力学模型组成，本研究首先建立其动力学模型。

2 动力学模型及其校验

2.1 动力学模型

根据火炮内弹道理论［22］，本文建立该小型火工作动器的内弹道动力学模型。将火药燃烧微分方程表达为：

式中：φ为整装火药的燃烧百分比；Z为火药相对厚度；λ，μ和χ为火药形状特征量；t为时间。因该作动器的火药形状为单孔管状，火炮内弹道理论定义该管状火药的形状特征量为：χ=1 +β，λ=-β/(1+β)，β=e1/c，Z=e/e1。其中的e1是火药初始厚度，e是火药燃烧厚度，c为火药初始长度，将特征量代入式（1）得到火药的燃烧百分计算式（2）。根据内弹道理论定义火药燃烧方程（3）。

式中：u0为火药的燃烧速度系数；n为火药燃速的压力指数；P为火药的燃烧压力。根据火药燃烧的基本方程和有关文献［23-24］，得到前腔燃气压力的变化率方程，并将其表达为：

式中：PZ为前腔压力；ωp为装药量；f为火药力；α为余容；ρ为火药密度；GM是燃气质量；x为活塞推杆的位移；xM为其最大位移；VZ为前腔的初始容积；AZ为前腔内活塞压力作用面积。

同理，将后腔燃气的压力变化率方程表达为：

式中：Pd为后腔内的燃气压力；Vd为后腔的初始容积；Ad为后腔内的活塞压力作用面积。

燃气通过节流孔的质量变化率方程为式（6）与式（7）［25-27］：

式中：GM为燃气质量；qm为在单位时间流出节流孔的燃气质量；k为绝热指数；A为节流孔面积；t为时间。

因前、后腔内的燃气作用，活塞杆输出推力和位移，其受力方程为：

式中：Fp为活塞杆的输出力。通过作动器的内弹道动力学模型，研究者首先得到前、后腔内燃气压力的变化规律，再由式（8）计算活塞的输出力，最后由输出力得到传动机构的输出角度、角速度等参数。旋转机构是一种螺旋传动机构，式（9）为其输出扭矩的计算式：

式中：M为输出力矩；d为螺旋中径；β为螺旋升角；μ为摩擦系数。

因理论计算采用计算机数值计算方法，文中将旋转机构的输出角速度和角度表达为：

式中：J为转动惯量；ω为输出角速度；θ为输出角度。

火工机构的初始状态为锁定状态，作动器剪断销钉后才能驱动旋转机构，设定活塞位移达到0.5倍的剪切直径时，销钉被剪断，将该判据表达为：

式中：Fpin为作动器需要克服的剪切力；Fcut为销钉的剪断力；dcut为销钉的剪切直径。研究者利用表1 中的参数完成了数值计算，图3是其计算流程。

表1 计算参数Table 1 Parameters for calculation

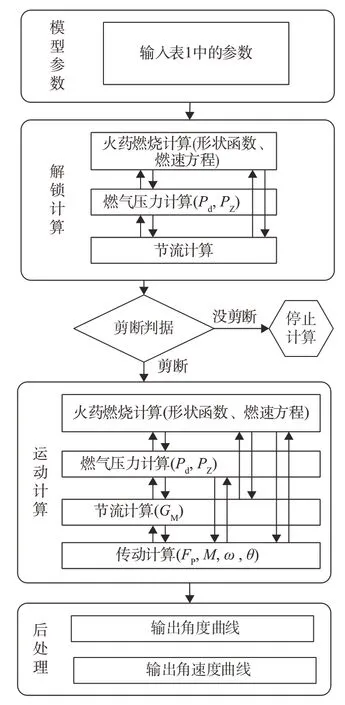
图3 计算流程Fig.3 Process for calculation

2.2 仿真校验

2.2.1 模型的建立

因表达旋转机构输出的增量方程会引入累积误差，文中用有限元法对作动器的动力学模型进行了校验。为了提高计算效率，首先对仿真模型作如下简化设定：

1) 转动副不是本文的研究内容，所以将其简化为单旋转自由度的点。同理，将滑动副简化为单平动自由度的点。

2) 忽略螺旋传动之外的摩擦力，不计重力场的影响。

3) 因仿真模型是力输入模型，在计算程序中设定剪断销钉的判据为：当FP≥Fpin+FM，则Fpin=0，其中的FM为等效负载。

4) 这种旋转机构的接触表面采用了良好的润滑措施，根据前期的研究成果，计算模型中忽略接触面的热效应［28］。

5) 简化翼的载荷为质量点。

依据上述的简化设定，研究者建立了机构的有限元分析网格。网格均采用八节点六面体单元，接触面是计算传动的关键部位，该部位采用了细化网格。驱动轴模型有117 000 个单元，螺母模型有50 100 个单元，驱动轴的接触面有1 000 个面单元，共6 000 个接触面单元。螺母的每个接触面有500 个面单元，共3 000 个接触面单元。为保证模型的计算精度，各单元的尺寸均小于1 mm。

机构材料为高强合金钢30CrMnSiA，文中设定这种金属为非线性弹性材料模型，表2 列出了这种材料的应变-应力数据，材料的密度为ρ=7.8 g/cm3，其泊松比为0.33，材料参数引自Total Materia 数据库。

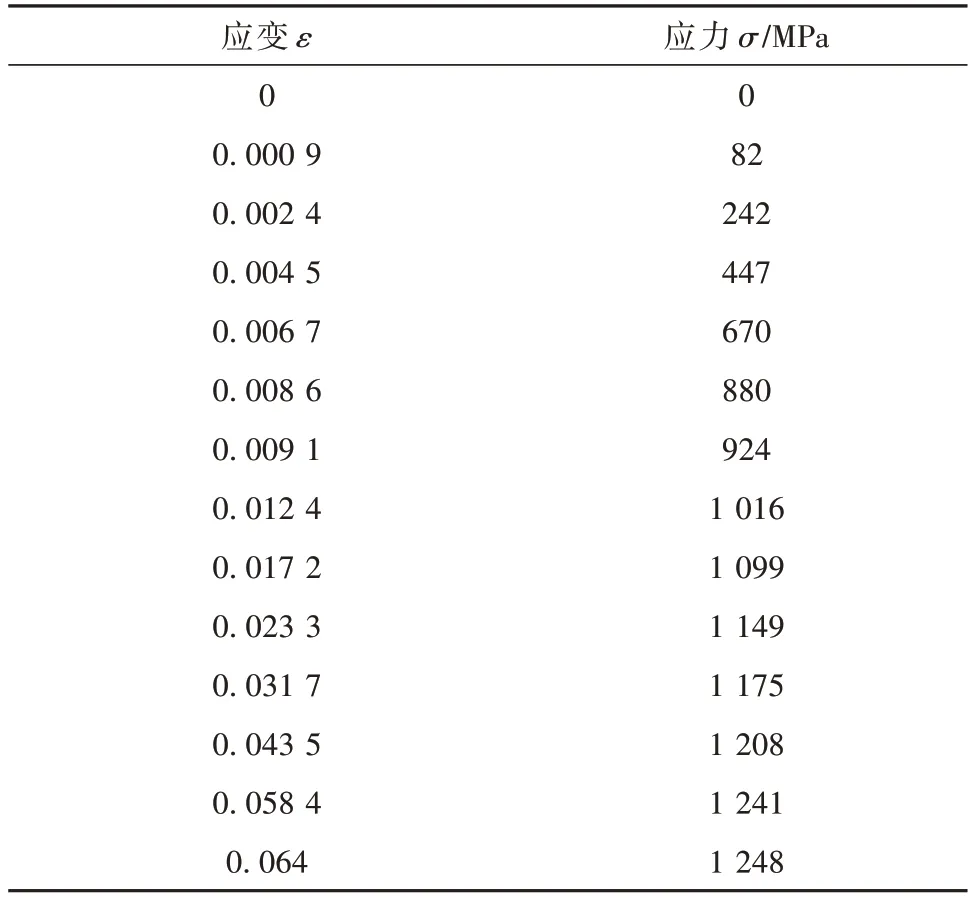
表2 30CrMnSiA的材料参数Table 2 Material parameters of 30CrMnSiA

模型的边界条件有约束和载荷边界。约束边界设定螺母具有Y轴的旋转自由度，并限制其X，Y，Z方向的平动自由度和X，Z轴的旋转自由度。设定螺杆有Y方向的平动自由度，并限制其X，Y，Z轴的旋转自由度和X，Z方向的平动自由度。

将FP施加在螺杆上，它驱动螺杆朝+Y方向平动。剪切力Fpin=1 600 N，它也施加在螺杆上，其方向和驱动力FP相反，当FP≥Fpin+FM，Fpin=0。Tm为气动载荷并施加在螺母上，并取Tm=±3 N·m，图4 是模型上的载荷示意。

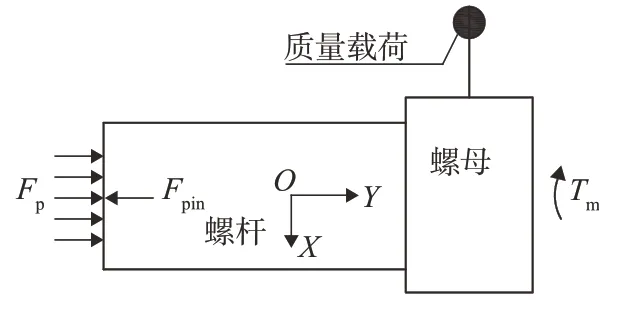
图4 施加在模型上的载荷Fig.4 Loads applied on the model

2.2.2 计算及其校验结果

研究者采用ADINA软件编写了校验程序和网格文件，校验模型的参数及其边界条件均符合上述内容。由于火工机构是一种高速传动机构，其计算步长宜采用小量设置，模型的计算步长小于1×10-3s。因该传动接触具有大接触应力、高速滑动的特点，其计算难于收敛，文中采用易于收敛的Bathe 隐式时间积分方法求解，同时利用ATS 算法控制计算步长，以提高计算效率和稳定性。

研究者分别计算和校验了逆风和顺风载荷下的结果。图5 是逆风和顺风载荷下展开角度的理论计算及其校验结果，图6 为逆风和顺风载荷下角速度的理论计算及其校验结果。计算结果表明：该火工机构可实现高速展开的功能，其逆风载荷下的到位角度达到了128.5°，理论计算的工作时间为121.5 ms，校验结果为109.5 ms。理论计算的最大角速度值为1 540（°）/s，其校验结果为1 740（°）/s。在顺风载荷下，该火工机构的到位角度为128.5°，理论计算的工作时间为114.5 ms，校验结果为103.1 ms。理论计算的最大角速度值为1 991（°）/s，其校验结果为2 144（°）/s。FEA 校验的速度高于理论计算值，其时间也少于理论计算值。逆风载荷下，工作时间的校验误差为10.9%，角速度的校验误差为11.4%。顺风载荷下，时间的校验误差为11.1%，角速度的校验误差为7.1%。

图5 展开角度的理论计算及其校验Fig.5 Output angles of calculation and verification

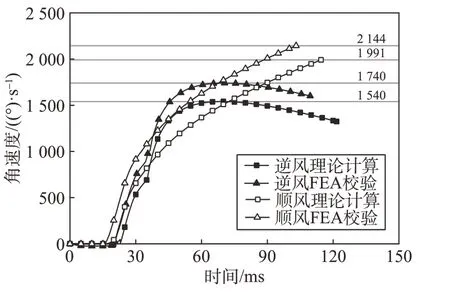
图6 展开角速度的理论计算及其校验Fig.6 Angular velocity of calculation and verification

3 试验验证

研究人员测试了该火工机构的性能，共完成了10 次试验，其中5 次是逆风试验，另5 次是顺风试验。图7 至图10 为试验和理论计算、FEA 校验结果的对比情况。

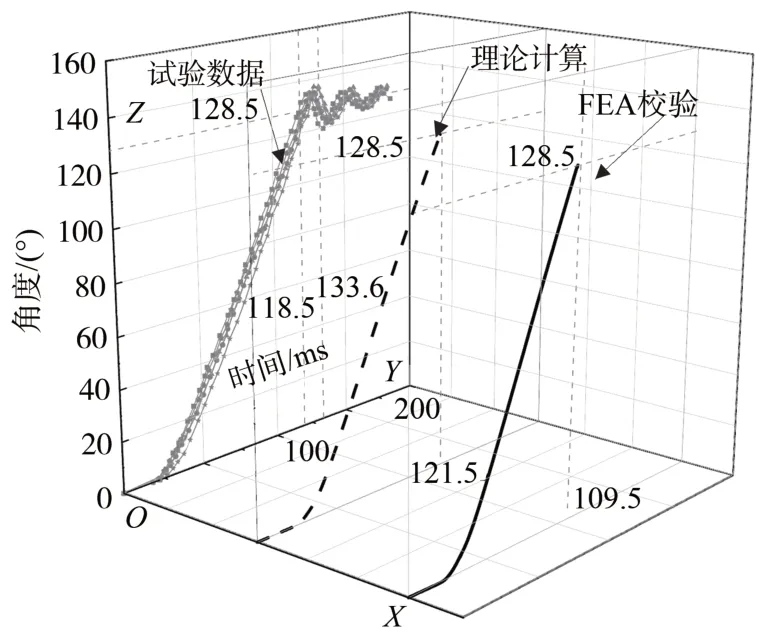
图7 逆风下的角度对比Fig.7 Comparison of angle under against wind

图7 和图8 说明了该机构在逆风载荷下的5 次试验结果：输出角度均达到了128.5°，工作时间为118.5～133.6 ms，最大角速度为1 271.4～1 375.9（°）/s。

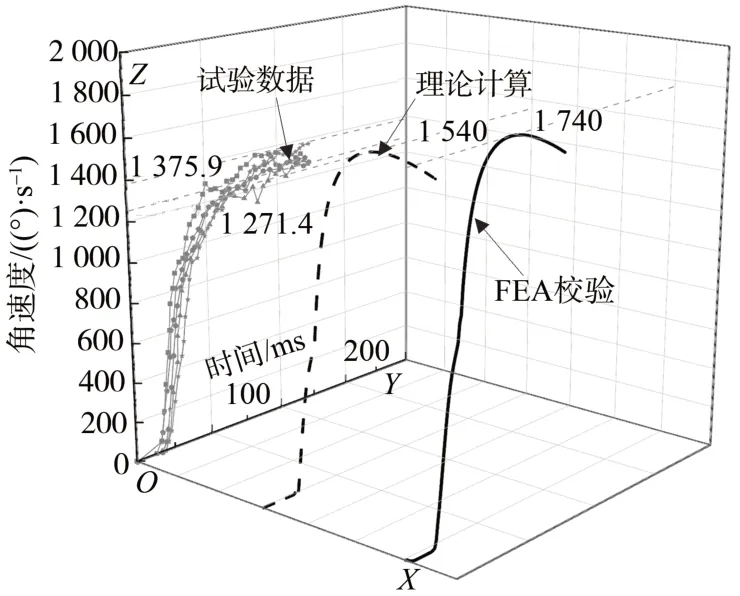
图8 逆风下的角速度对比Fig.8 Comparison of angular velocity under against wind

图9和图10是该火工机构在顺风下的5次试验结果：其输出角度均达到了128.5°，时间为82.3～90.6 ms，最大角速度为2 039.1～2 411.6（°）/s。

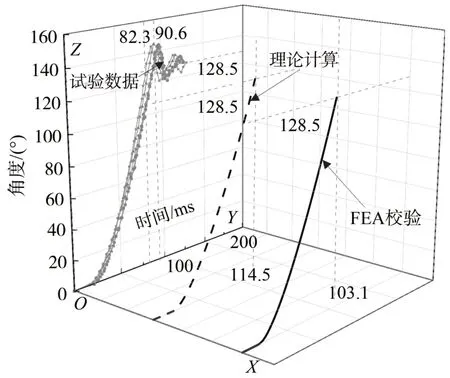
图9 顺风下的角度对比Fig.9 Comparison of angle under following wind

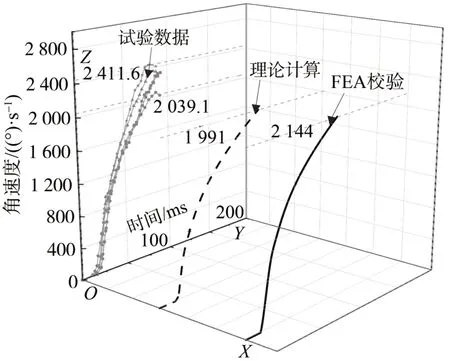
图10 顺风下的角速度的对比Fig.10 Comparison of angular velocity under following wind

逆风负载下的理论计算结果和试验数据基本吻合，其时间的计算值处在试验数据的区间内，其角速度的计算值略高于试验数据。顺风下的理论计算结果和试验数据的差异较大，其差异表现为理论计算的时间明显长于试验结果，相应的速度也明显低于试验结果。

4 结果讨论

旨在解决展开机构的小型化难题，本文研究了一种小型火工机构。首先建立了该火工机构的输出模型，研究者进行了理论计算并对其结果进行了校验。理论计算和试验结果表明：在不同负载下，这种火工机构均能正常工作，其工作角度为128.5°，其时间均不大于200 ms，其最大角速度均不超过3 000（°）/s，火工作动器的自适应阻尼性能减少了冲击。该火工机构具备了小型化的特点，研究成果可直接应用于薄型折叠翼面。针对上述结果，本文开展了以下讨论：

1) 火工机构的性能存在离散性。逆风下的工作时间的范围为118.5～133.6 ms，角速度为1 271.4～1 375.9（°）/s。顺风下的工作时间范围为82.3～90.6 ms，角速度为2 039.1～2 411.6（°）/s，该现象说明该火工机构的输出具有离散性，该特性主要源自火工品的离散特性及其他工程因素。在工程应用中，该火工机构的输出必须有足够的裕度，本研究的指标为工作时间不超过200 ms，最大角速度不超过3 000（°）/s，机构的最大工作时间不超过133.6 ms，其最大角速度不超过2 411.6（°）/s，其输出具有足够的裕度，该火工机构可消除离散性带来的风险。

2) 火工机构的工作过程具有自适应阻尼特性。该机构的动力装置是一种火工装置，其节流孔的面积决定活塞杆的运动速度，活塞的高速运动将升高前腔内的燃气压力，从而增加活塞的阻尼力，该效应和节流孔的面积相关。该作动器的活塞杆末端设计有缓冲结构，该缓冲结构使作动器具有末端缓冲性能。逆风载荷下的这种阻尼特性具有显著特征，图8表明机构输出的角速度逐步降低，在其末端出现明显的减速现象。图10 中的角速度曲线的弯曲形状说明其角加速度逐步降低，但其末端缓冲现象并不显著，这是顺风惯量的冲击减弱了其末端缓冲效果。

3) FEA 校验模型和理论模型的剪切判据不同，该区别产生了两者结果的差异。因FEA 模型的输入变量为作用力，FEA 校验模型以作用力为判断参数，当FP≥Fpin+FM，FEA 校验模型判定销钉剪断。理论计算模型以位移为判断参数，理论计算模型满足FP≥Fpin+FM和x≥0.5dcut，即推力大于合力并产生大于1 mm的位移时，计算模型判定销钉剪断。以上原理说明：相比于FEA 校验模型，理论模型的销钉剪断判据具有延迟性，图5～图6显著表现了这种延迟特性，理论模型计算的展开时间长于FEA 模型的计算值，其角速度也高于FEA模型的计算值。

4) 文中的火工机构用销钉锁定其初始位置，该锁定结构主要影响顺风载荷下的性能。因理论模型设定剪切力为最大值，该剪切力必然大于实际值，这导致了顺风载荷下理论计算结果和试验数据的差异。计算模型设定剪切力为最大值的90%，并以两种负载进行计算，计算的结果为图11～图14。图11 和图12 表明：在逆风载荷下，即使减少剪切力为最大值的90%，其值和100%剪切力计算结果的差异仍较小，该结果说明剪切力对其影响较小。图13和图14 是顺风载荷下的结果对比，图中的数据表明：90%剪切力的计算结果和试验数据一致，其值和100%剪切力的计算结果具有较大的差异。上述分析表明：该火工机构的锁定结构主要影响其顺风下的输出。剪切力是随剪切位移的增大而减少，而理论模型的剪切力采用了最大的恒值，其阻力作用必然大于实际效果，该误差显著影响到计算结果。该现象也说明剪切力的大小影响到翼面的正常展开，即影响翼展机构的功能可靠性。在工程应用中，剪切销的剪切直径和剪切力应作为重要控制参数。

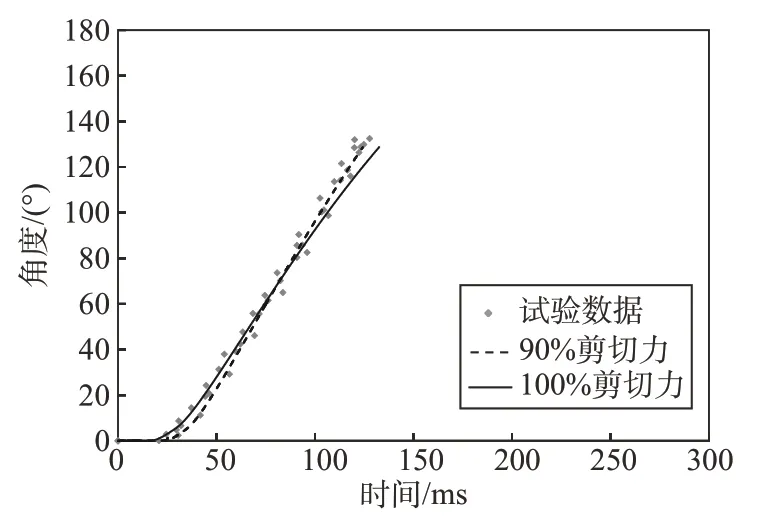
图11 逆风下两种剪切力的输出角度Fig.11 Angles used two cutting forces under against wind

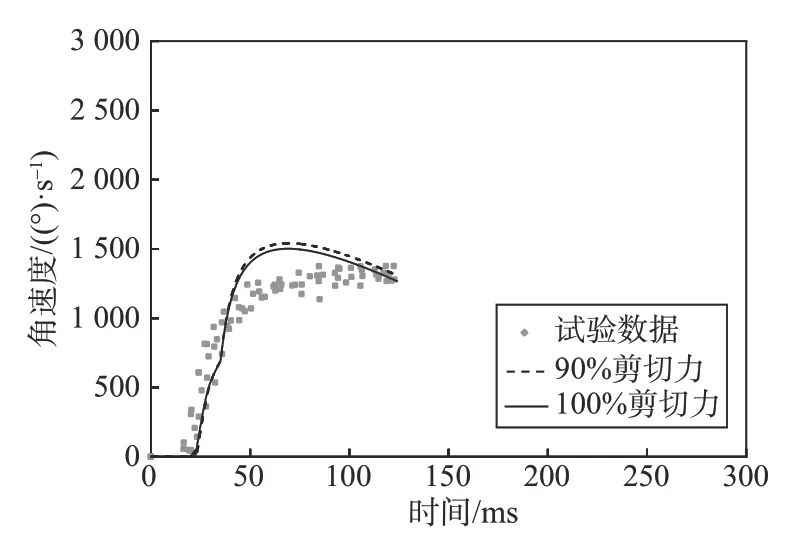
图12 逆风下两种剪切力的输出角速度Fig.12 Angular velocity used two cutting forces under against wind

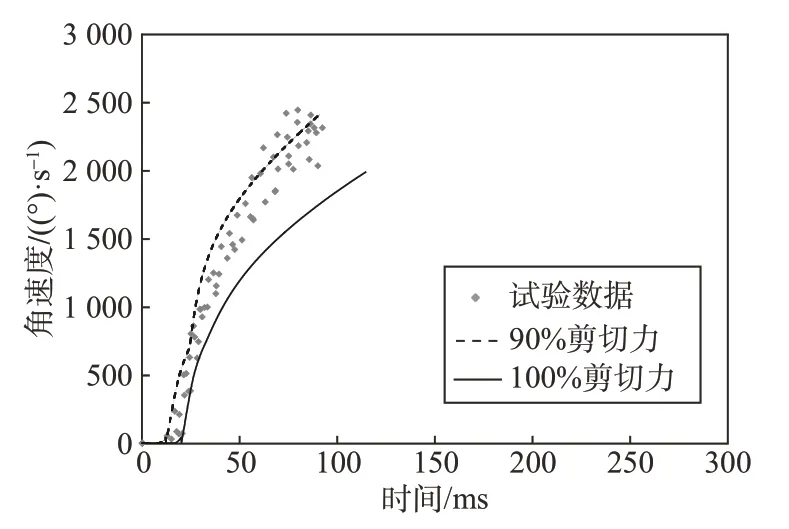
图14 顺风负载下两种剪切力的输出角速度Fig.14 Angular velocity used two cutting forces under following wind

5 结论

1) 文中研究的火工机构具备简单、小体积的优点，解决了薄翼面的结构设计难题。文中也建立了该火工机构的理论模型，该理论模型可作为工程设计的参考。

2) 因剪切销的锁定结构具备简单、可靠的特点，本研究采用销钉锁定其初始位置。研究证明销钉的剪切力误差会影响到顺风性能，将来需要研究高精度的剪切力模型以完善理论计算模型。剪切力影响翼展机构的功能可靠性，将来也需要研究剪切销的可靠性试验方法，这是其工程应用的重要研究内容。