平板式“快集快响”微小卫星布局优化设计方法

张浩，周军，2，刘光辉，2，程承，2，白杨，冯振欣，2

（1.西北工业大学航天学院，西安 710072；2.微小卫星技术及应用国家地方联合工程实验室，西安 710072）

0 引言

近年来，微小卫星在近地观测、高轨中继与深空探测等不同轨道高度的宽域飞行任务中得到了广泛应用［1-2］。随着任务场景日益复杂，特别是紧急救援（地震、洪水、雪灾或瘟疫等）与安全事件（军事冲突与战争）等难以提前预测的突发任务，微小卫星的快速设计、集成与部署等面临更加严格的挑战［3］。现有的微小卫星大多根据确定的飞行任务定制生产，并需要经过“需求分析-概念原型-仿真校验-部组件设计-整星方案-样机研制-测试验证-部署发射”等一系列复杂的设计流程［4-5］。然而，一旦飞行任务发生紧急调整，处于研制过程中的卫星功能与构型难以在短时间内二次重构，不能满足快速性的要求。因此，需要开发新的微小卫星以快速响应可能面临的紧急飞行任务［6］。

“快集快响”（Fast assembly and rapid response，FARR）卫星是一种新的微小卫星概念，主要针对各类突发事件，实现卫星的快速研制、发射与应用［7］。随着微小卫星的应用领域越来越广，传统的盒式微小卫星（如立方星等）受其构型的约束与限制，所能提供的性能上限难以满足宽域飞行任务的应用需求［8］。因此，国内外学者一直致力于研究新型的微小卫星构型，以提高卫星的应用性能［9-11］。

平板式卫星是一种新兴的FARR 微小卫星，由于采用了标准的板状构型，只需要将不同功能的组件在板块上集成安装，即可形成具有特定功能的卫星。相较于传统微小卫星，平板卫星具有更大的表面积，便于安装太阳能电池、天线，设计散热回路，能够适应不同轨道高度的飞行任务。与此同时，由于支持一箭多星堆叠发射，能够快速组网，平板式构型逐步成为未来面向宽域任务的FARR 微小卫星的主流趋势。截至目前，国内外已经有多颗平板式FARR 微小卫星得到成功应用，包括星链、碟式卫星（DiskSat）等［12-13］。

然而，由于结构的特殊性，平板式FARR 卫星在水平方向上的转动惯量远大于传统微小卫星。此外，由于部组件的功能、尺寸、结构与质量等存在差异，部组件在卫星上的布局会进一步对卫星的质量、重心与转动惯量（Moment of inertia，MOI）等关键指标产生较大影响。因此，如何合理规划部组件在平板卫星上的布局，使卫星获得更好的性能成为FARR卫星设计过程中面临的主要问题［14］。

目前已有一些针对卫星布局优化设计的研究，主要方法是将卫星平台看作集成舱，通过将不同的卫星组件安装到集成舱中，可把卫星布局优化设计问题转化为三维舱包装问题，这属于NP-hard 问题［15-16］。文献［17］采用遗传算法对卫星的部组件进行匹配优化，获得了部组件的最佳组合形式以及安装位置。文献［18］提出一种双种群遗传算法对元件进行布局，改善并提高了散热性能。文献［19］通过在优化过程中给卫星动态分配组件的方式获得更好的卫星性能。文献［20］采用启发式算法完成部组件的最优分配，并通过进化算法求解集成后卫星的关键指标。文献［21］采用粒子群优化和基于梯度的顺序二次编程的混合算法对部组件进行快速定位，并考虑了结构刚度与固有频率等约束。文献［22］采用加速粒子群优化算法来搜索最优布局方案，减少了残余磁场对卫星姿态产生的影响。文献［14］针对多模块微小卫星提出了一种基于“Tabu搜索+差分进化+自适应尺寸调整”的混合优化方法，其中Tabu搜索算法考虑部组件高度与模块可容纳高度，完成了部组件的最优匹配；差分进化算法解决多模块微小卫星的布局优化问题；自适应调整对模块尺寸做进一步完善，解决了多模块卫星的布局优化问题。

虽然已经有多种优化方法用于卫星布局优化，但是大多数布局优化方法的研究对象仍是盒式构型卫星，且都集中在卫星传热、功耗与剩磁等指标的优化设计中。随着模块化微小卫星技术的成熟，FARR 卫星平台逐步升级为由多个功能模块装配形成的多模块卫星［23-24］。然而，多模块卫星存在更加复杂的耦合关系，不仅需要考虑到部组件在模块的布局问题，还需要兼顾部组件与模块的质量匹配问题，以获得更好的卫星结构性能［21］。此外，现有研究大多以单模块卫星为主，对于多模块卫星的布局优化问题少有提及。因此，需要开展多模块FARR卫星的布局优化方法研究。

本文提出一种基于级联遗传算法（Cascade genetic algorithm，C-GA）的微小卫星布局优化设计方法，并将其应用于多模块平板式FARR 卫星的布局优化设计中。该方法基于经典的遗传算法进行改进，相较于文献［14］的混合算法与经典GA 算法，所提方法采用迁移、交换与调整3种操作，进一步提高了算法的收敛性能与寻优能力。论文首先针对FARR 卫星的结构特点，建立卫星质量特性与转动惯量的布局优化模型；随后通过所提方法规划部组件在功能板块上的布局与安装位置，形成最优布局方案；最后通过算例仿真与工程实例验证所提方法的性能与有效性。

1 FARR卫星布局优化模型

FARR 卫星采用模块化装配的形式进行集成，功能板块成为卫星的基本单元。结合部组件、功能板块以及卫星的结构特性，提出以下假设：

假设1：功能板块与卫星均为刚体结构；

假设2：卫星包络被视为矩形薄板结构，部组件被视为长方体结构；

假设3：部组件和功能板块具有均匀的密度，其重心和几何中心为同一点。

卫星布局优化的目标是将部组件分配到功能板块，并将它们设计到最佳位置，需要满足以下要求：

要求1：同一个功能板块内的部组件之间以及部组件与板块之间均不存在机械约束；

要求2：卫星获得最小的质量差异以及最小的转动惯量。

1.1 坐标系定义

FARR卫星的三维坐标如图1所示。卫星由4个功能板块组成，功能板块边框中间设计用于安装电推力器的槽型腔体，卫星的部组件被集成在功能板块中间的集成区。

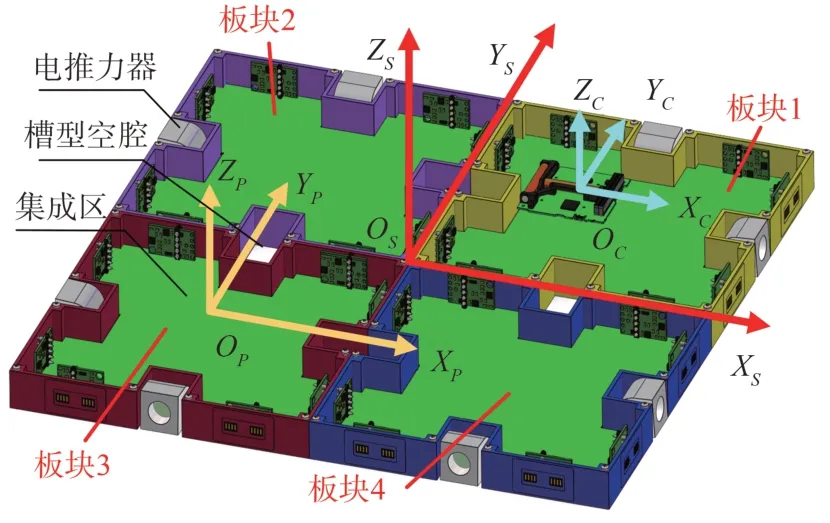
图1 卫星坐标系示意图Fig.1 Diagram of the satellite coordinate system

1) 卫星参考坐标系OSXSYSZS：原点OS位于功能板块的相交点，ZS轴与卫星的垂直轴重合；

2) 板块参考坐标系OPXPYPZP：原点OP为板块重心，OPXP轴与OSXS平 行，OPYP轴与OSYS平 行，OPZP轴与OSZS平行；

3) 部组件参考坐标系OCXCYCZC：原点OC为部组件的重心，OCZC与OSZS重合，OCXC与OSXS之间存在夹角θ。

1.2 优化参数设计

以C={c1，c2，…，cn}代表卫星部组件的集合，η={η1，η2，…，ηk}代表部组件所在板块的集合。部组件仅考虑以0°或者90°两种角度进行安装。所需的卫星布局优化参数见式（1），部组件的纵坐标如式（2）所示：

式中：K表示所有部组件重心坐标集合（同时也是安装位置集合）；kci表示部组件ci的安装位置属性；(xi，yi，zi)表示部组件ci的重心（安装）位置坐标；θi表示OciXci与OSXS轴之间的角度；板块边框厚度为Hj，hi为部组件高度。

1.3 性能指标

以降低卫星的转动惯量作为优化目标，需要获得卫星的重心位置以及转动惯量模型。卫星的重心位置(xS，yS，zS)可根据式（3）获得：

根据叠加定理与平行轴定理，卫星的转动惯量模型如式（4）～（5）所示：

式中：I(K)是卫星的转动惯量；Ix(K)，Iy(K)，Iz(K)为卫星 在3 个方向 的转动惯量；(Ix，M，Iy，M，Iz，M)、(Ix，C，Iy，C，Iz，C)、(Ix，Bl，Iy，Bl，Iz，Bl)、(Ix，Pr，Iy，Pr，Iz，Pr)分别为功能板块、部组件、槽型空腔与电推力器在3个方向的转动惯量。

1.4 约束条件

根据要求1，部组件之间需要满足的约束条件如式（6）所示：

式中：vij(K)表示部组件的机械干扰约束，若式（6）

值为0，表示卫星所有部组件之间以及部组件与功能板块之间均不存在机械约束。

1.5 优化模型

根据要求1 与要求2，卫星布局优化模型如式（7）～（8）所示：

其中，M(K)与O(K)分别通过式（9）与（10）获得：

式中：M(K)是质量目标函数，由4 个板块的质量标准差表示，用于反映卫星板块之间质量的均衡性；ml是包括部组件在内的板块总质量是卫星质量的均值；O(K)是转动惯量目标函数；o1(K)表示卫星的矩阵3轴转动惯量；o2(K)表示3个转动惯量的标准差。o1(K)与o2(K)如式（11）与（12）所示：

2 FARR卫星布局优化设计方法

为了兼顾功能板块的质量均衡以及卫星的转动惯量，提出一种基于级联遗传算法（C-GA）的FARR 卫星布局优化设计方法。布局优化过程采用两级遗传，以缩小可行解空间，达到快速收敛。一级遗传采用“迁移”操作为功能板块适配部组件，使卫星具有最佳的质量均衡性。二级遗传采用“交换+调整”操作进一步优化部组件在功能板块的布局与安装位置，以获得最小的转动惯量。

2.1 迁移

假定种群规模为ξR，迭代次数为iRmax。在迭代优化前，随机生成初始解，执行迁移过程。设定迁移率，将其作为部组件是否需要迁移的判断条件。当迁移率不小于随机生成的迁移系数时，执行迁移操作。部组件的迁移策略为：将具有最大质量的功能板块中的最大质量部组件与具有最小质量功能板块中的最小质量部组件进行互换，以完成迁移。迁移过程如式（13）所示：

式中：ηtemp是中间变量表示最小质量部组件的板块号表示最大质量部组件的板块号；GR是随机生成的迁移系数；GRset是设定的迁移率；cmax=max{c1，c2，…，cnPmax}表示质量最大的部组件；cmin=min{c1，c2，…，}表示质量最小的部组件；Pmax=max {P1，P2，P3，P4}表示质量最大的功能板块；Pmin=min {P1，P2，P3，P4}表示质量最小的功能板块。

经过迁移操作后，通过解算式（9）以获得最新的质量目标函数值。如果质量目标函数减小，则保留当前迁移过程，并更新部组件的匹配方案以及质量目标函数值。如果质量目标函数增大，则淘汰当前迁移的结果，并保留原有方案，随后进入下一次迭代，直到达到迭代次数上限。

2.2 交换

假定种群规模为ξE，迭代次数为iEmax。在进行交换前，生成可行的初始位置布局。设定交换率作为部组件位置交换的判断条件。当交换率不小于随机生成的交换系数时，执行交换操作。部组件交换策略为：随机选择任意功能板块内质量不相等的2 个部组件进行位置互换，并计算交换位置后的卫星转动惯量，直到达到最大迭代次数。部组件的交换操作描述如式（14）所示：

式中：cε表示选中的功能板块Pε的部组件集合，ci与cj表示从部组件集合cε中随机选择的2 个质量不等的部组件，GE表示随机生成的交换系数，GEset为设定的交换率。

2.3 调整

调整操作用于对交换后的部组件位置进行小范围微动，以获得更大的解空间，防止陷入局部最优。设定调整率作为部组件是否发生位置调整的判断条件。当调整率不小于随机生成的调整系数，执行调整操作。位置调整策略为：随机选择功能板块Pα的一个部组件ci，使其安装位置坐标发生变化。部组件kci在位置坐标改变后，新的位置信息可表示为计算方法如式（15）所示：

此外，部组件在完成任意迁移、交换与调整操作后，均需要对约束条件进行检测，以确保部组件、功能板块以及槽型空腔之间均不存在机械约束。

2.4 算法实现流程

通过流程图展示布局算法实现过程，如图2所示。

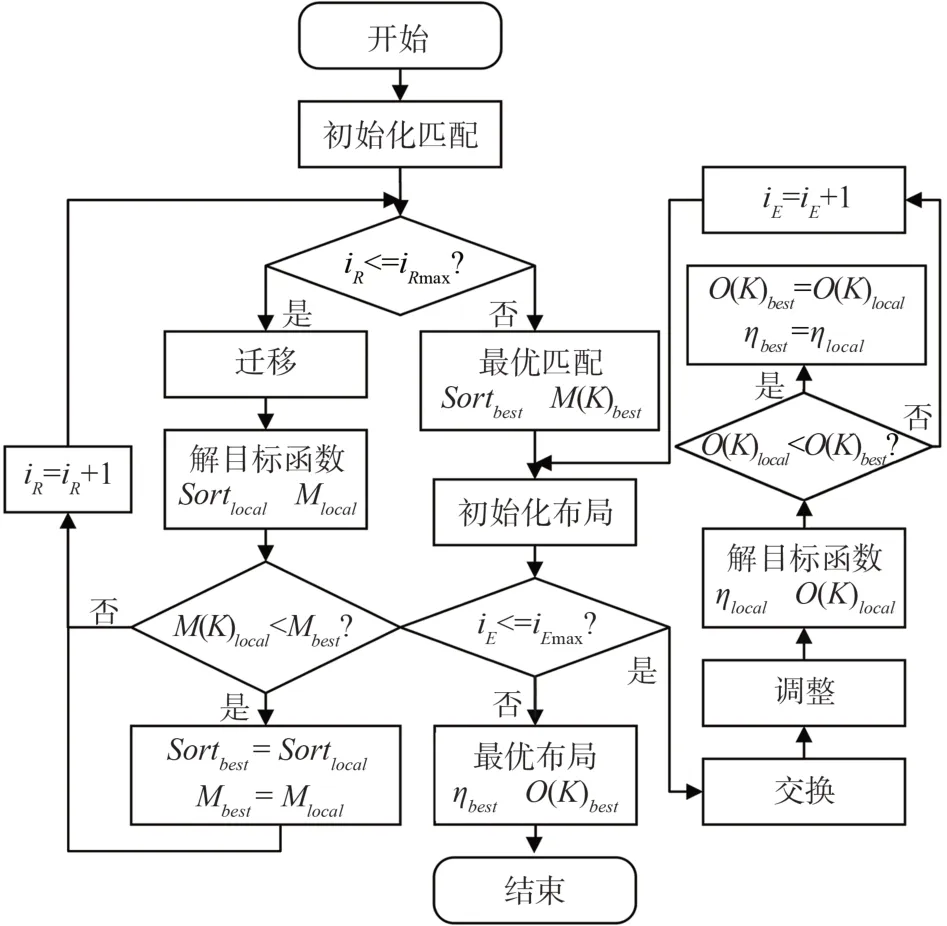
图2 卫星布局优化算法流程图Fig.2 Flow chart of the satellite′s layout optimization algorithm

3 仿真校验

3.1 仿真算例

以4 个功能板块组成的平板卫星作为FARR 卫星仿真算例，通过数学仿真验证所提布局方法的性能。其中功能板块的边长是400 mm，高为50 mm。FARR 卫星内集成20 个部组件，部组件的基本参数如表1 所示。设定种群规模为200，迭代次数为5 000，迁移率、交换率与调整率均被设定为1.0。根据调整原则，取最大尺寸的10%作为位置调整幅度范围，即-10 mm ≤u≤10 mm。在迭代过程中，分别执行迁移、交换与调整操作，直到达到迭代次数上限。为了表示部组件的3 个操作的实现过程，以板块2为参考，以执行任意一次优化过程为例，部组件的布局优化实现流程如图3所示。

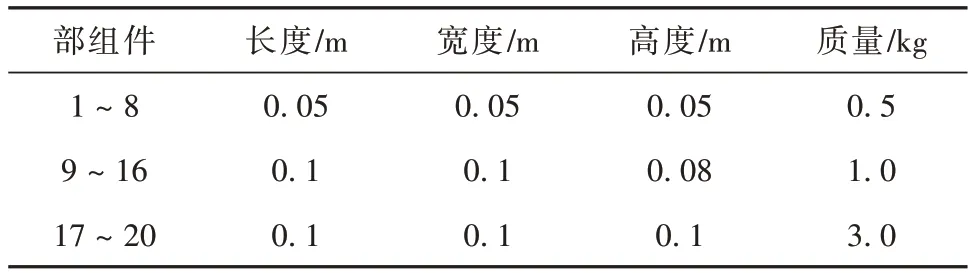
表1 部组件基本参数Table 1 Parameters of the components

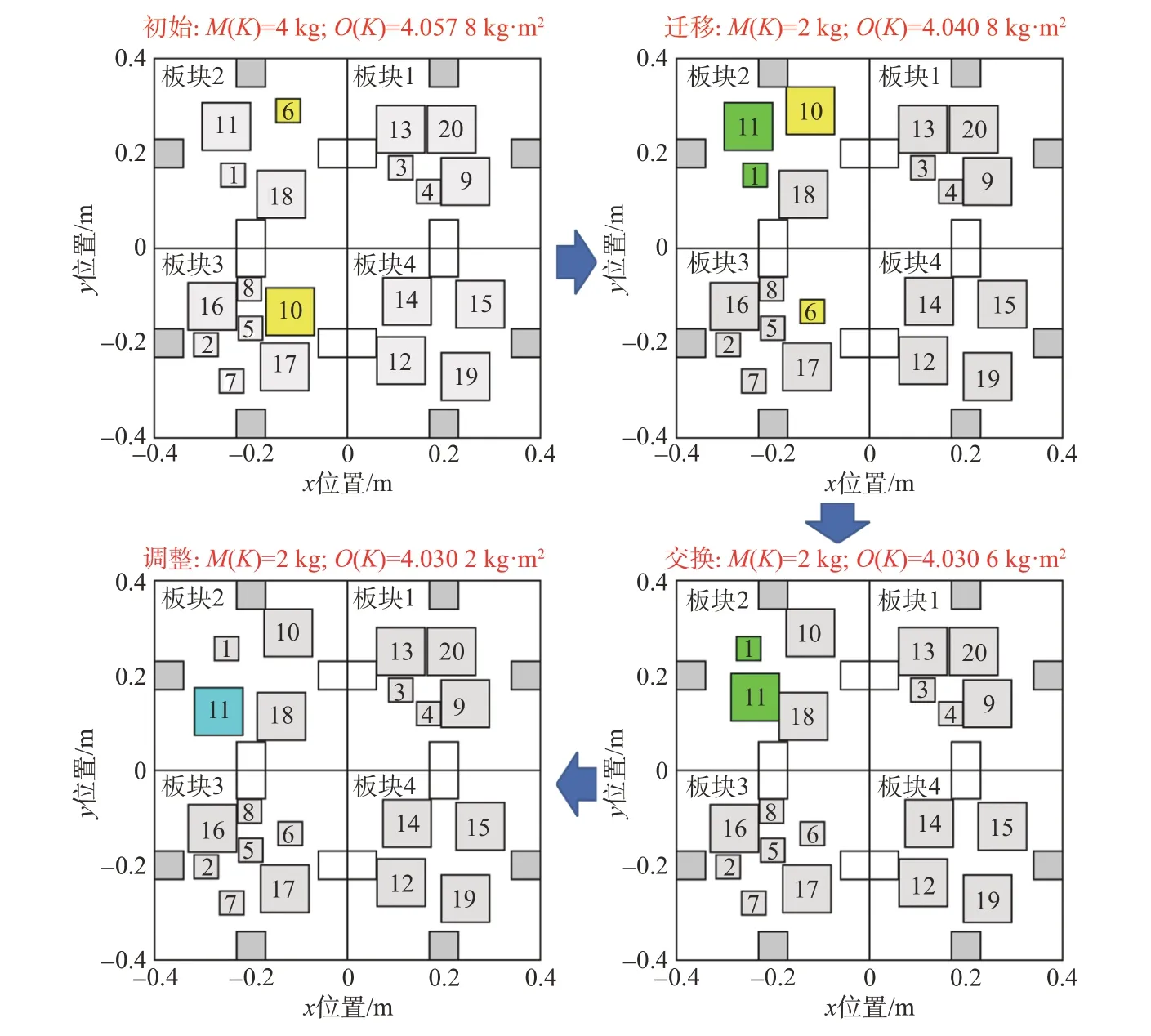
图3 布局优化方法实现流程图Fig.3 Flow chart of the layout optimization method

可知，执行任意迁移、交换与调整操作，均可以使卫星的MOI 目标函数减小。在达到迭代次数上限后，可以获得卫星部组件的最优布局方案，卫星的二维平面布局如图4 所示。此时，优化后的质量目标函数M(K)为0 kg，转动惯量目标函数O(K)为3.932 3 kg⋅m2。

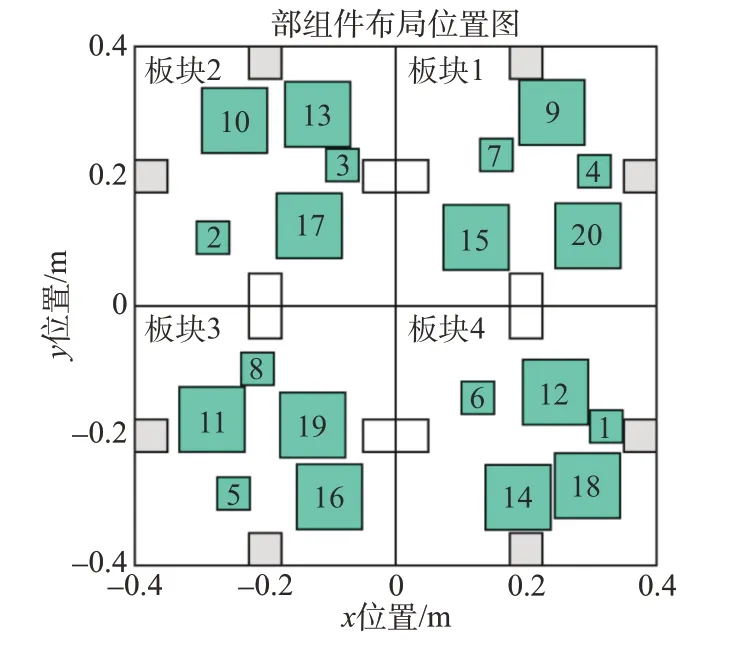
图4 部组件布局位置图Fig.4 Layouts of the components

为验证算法的性能，将所提布局优化方法与文献［15］提出的混合（Hybrid）算法以及经典GA算法进行对比。对比条件如下：在50，100，150，200 这4 种不同种群规模下进行对比，迭代次数设定为5 000。每组输入参数分别运行10 次后取其平均值，比较C-GA 与其他2 种布局优化方法的优化结果，算法优化性能对比曲线如图5所示。

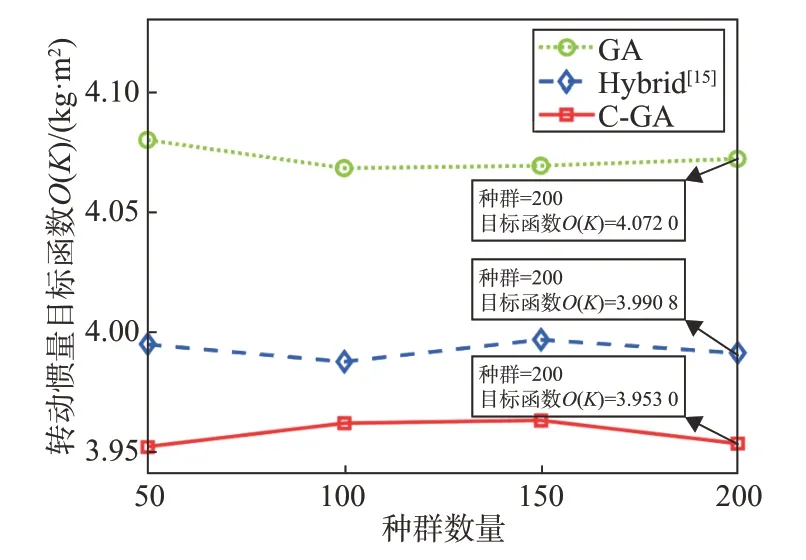
图5 算法优化性能对比曲线Fig.5 Comparison curves of the optimization performance of the algorithms

根据对比结果，C-GA算法能够获得最小的转动惯量。相较于GA 算法，C-GA 算法的性能提升了3.0%，且与Hybrid 算法的优化结果接近，因此两种算法均具有较好的寻优能力。

为验证3 种优化方法的收敛速度，对其收敛性能进行对比。设定种群规模为200，迭代次数为500，算法收敛性能对比曲线如图6所示。

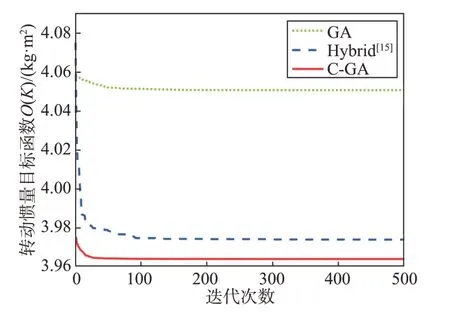
图6 算法收敛性能对比曲线Fig.6 Comparison curves of the convergence performance of the algorithms

图6 中，经典GA 算法的收敛速度相对较快，但是收敛后的转动惯量最大。Hybrid 算法采用Tabu搜索算法获得最优匹配方案，再通过差分进化算法得到最优布局方案。其初始值最大，收敛后的转动惯量与C-GA 算法基本接近，具有更出色的寻优能力。C-GA算法通过迁移操作获得最优匹配方案，再利用交换与调整操作实现布局优化，获得了最小的转动惯量，且能够快速达到收敛。因此，从寻优能力与收敛速度综合考虑，C-GA算法达到最优的代价最小，具有较好的性能。

3.2 工程实例

以遥感FARR 卫星为工程实例，验证所提方法的有效性。假定FARR 卫星由4 个功能板块组成，功能板块的边长为400 mm，高为50 mm。FARR 卫星内需要28 个部组件，参数如表2 所示。设定种群规模为200，迭代次数为5 000。迁移率、交换率与调整率均被设定为1.0。根据调整原则，位置调整范围设为-12 mm ≤u≤12 mm。采用所提算法进行优化，并对比50，100，150 与200 四种不同种群数量下的运算结果。对比条件如下：仅完成初始化匹配、执行“迁移”、执行“迁移+交换”与执行“迁移+交换+调整”。卫星的转动惯量目标函数在执行不同优化操作后的仿真结果如图7所示。

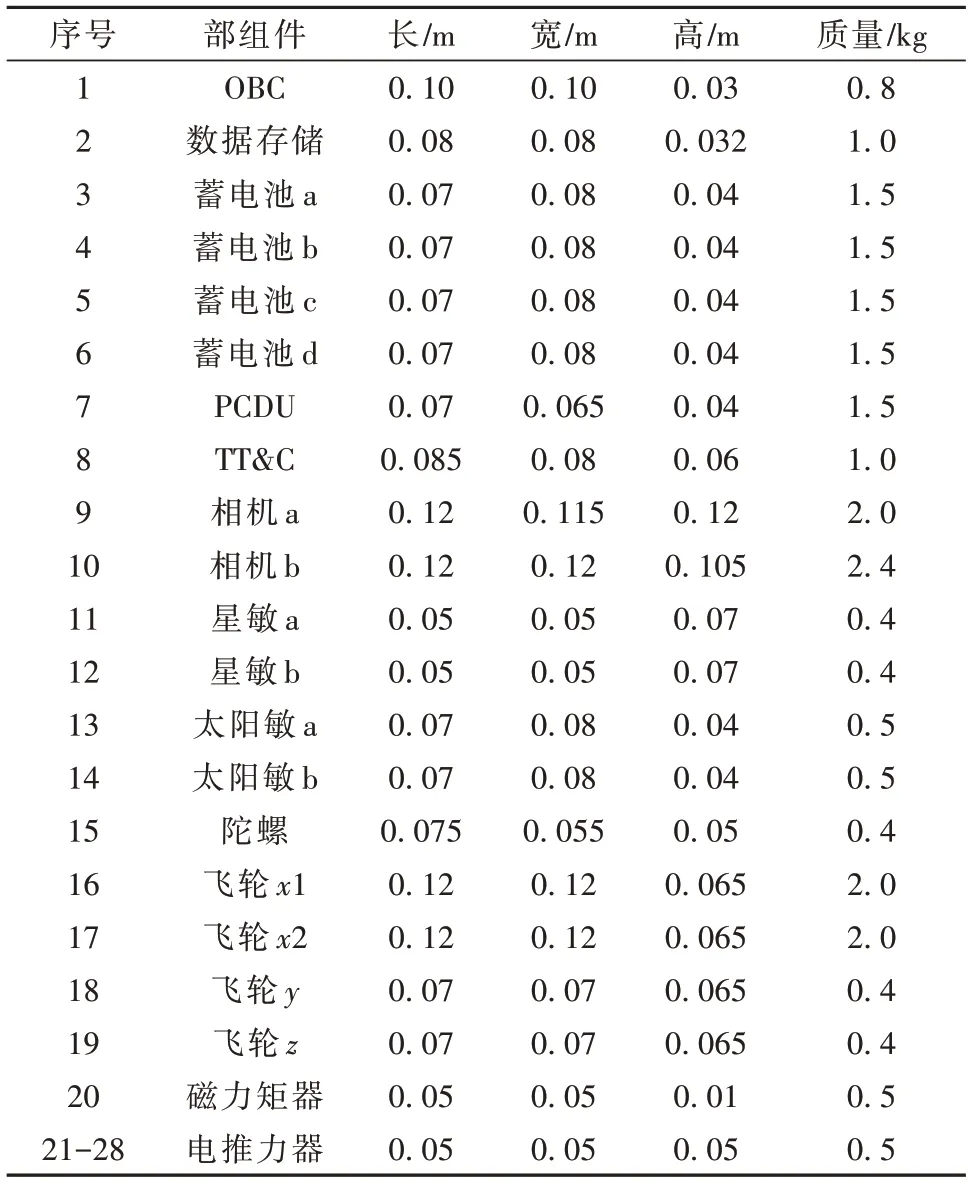
表2 遥感卫星部组件参数表Table 2 Parameters of remote sensing satellite components

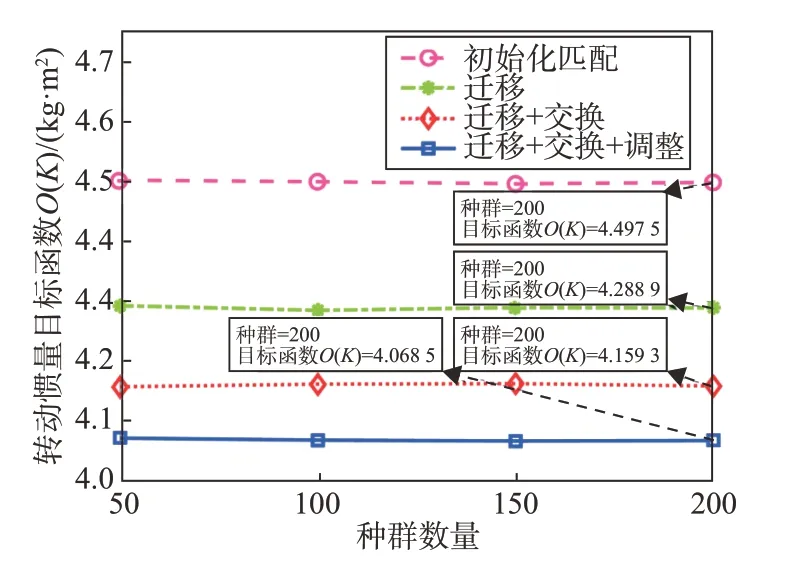
图7 不同优化操作下的仿真结果Fig.7 Simulation results under different optimization operations

在不同种群数量下，仅完成初始化匹配的卫星转动惯量目标函数要高于其他3种经过优化操作的结果，完成“迁移+交换+调整”3 种操作的转动惯量优化结果最小。以种群数量为200的优化过程作为参考，执行不同阶段优化操作下的转动惯量目标函数比不执行优化操作的结果分别减小了4.64%、7.52%与9.54%。由此可知，所提方法对于减小FARR卫星转动惯量是有效的。

根据所提方法优化所得的部组件最优安装位置如表3 所示。根据优化结果形成的FARR 卫星三维布局方案如图8 所示。此时，卫星的M(K)为1.00 kg，O(K)为4.068 5 kg⋅m2。

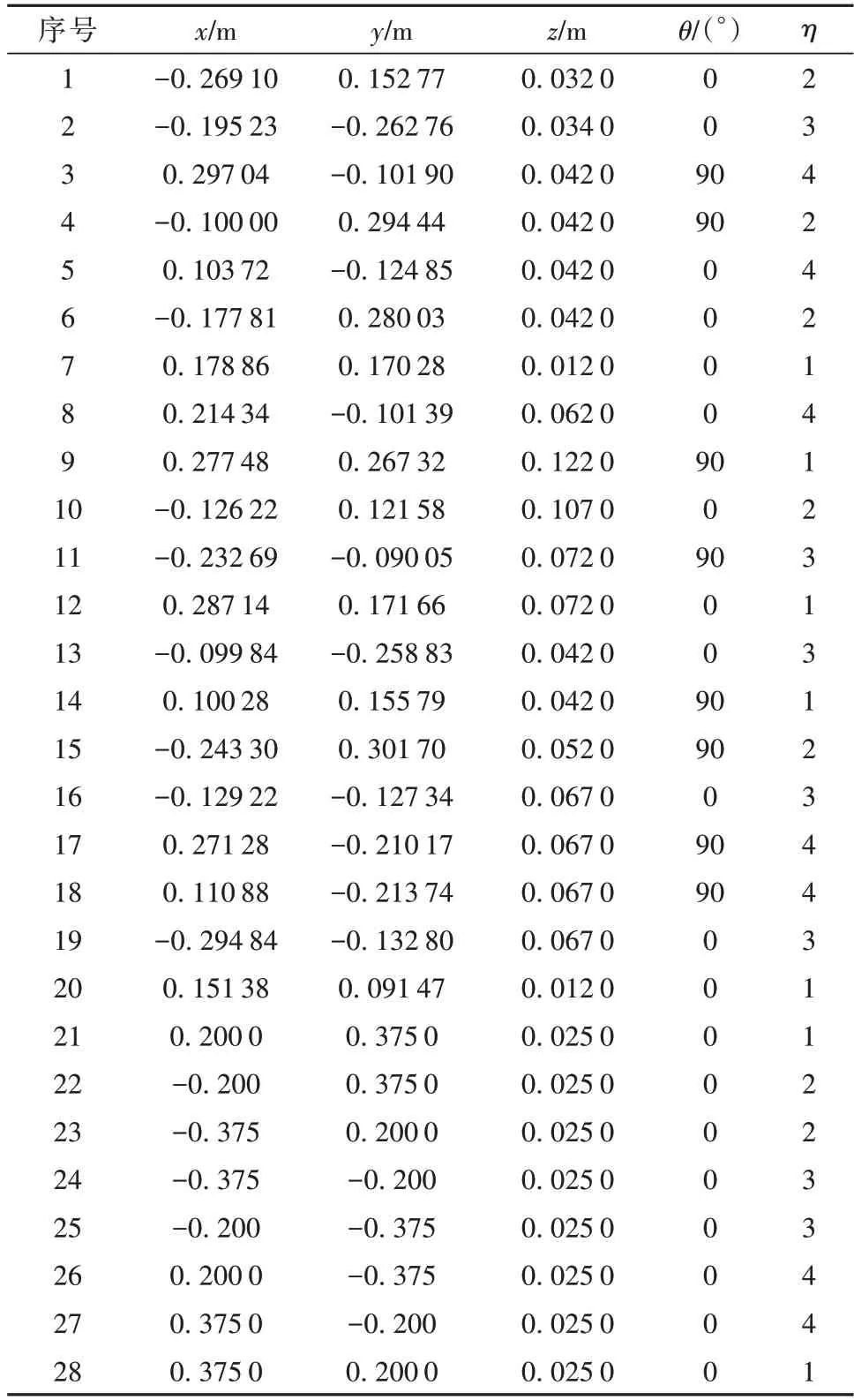
表3 遥感卫星部组件布局位置Table 3 Components′ layouts of remote sensing satellite

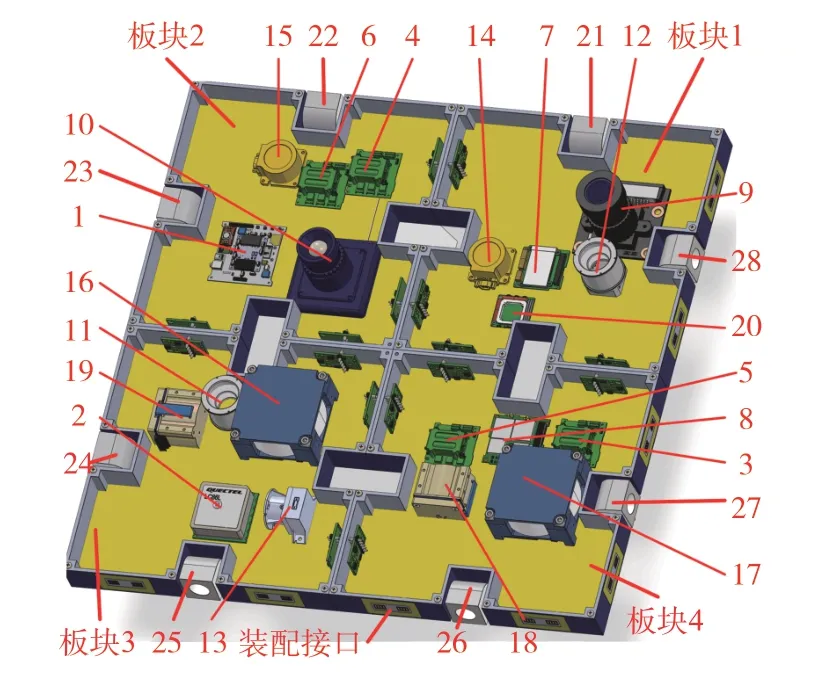
图8 遥感FARR卫星三维布局优化图Fig.8 Optimized 3D layout of remote sensing FARR satellite

4 结论

本文提出了一种基于C-GA 的布局优化方法，允许在不同功能板块间迁移部组件以及在同一功能板块内互换与调整部组件位置，实现了部组件在卫星中的最优匹配与最优布局。将所提方法与经典GA 算法以及Hybrid 算法在不同种群规模下进行对比，所提优化方法在收敛速度与优化性能方面均具有优势。通过工程实例，所提方法可使FARR 卫星的转动惯量降低9.54%。因此，可以有效解决平板式FARR卫星的布局优化问题。