小天体柔性着陆任务规划的动态时间约束推理方法

王棒，徐瑞，李朝玉，朱圣英，梁子璇

（1.北京理工大学宇航学院，北京 100081；2.深空自主导航与控制工信部重点实验室（北京理工大学），北京 100081）

0 引言

小天体探测是深空探测的重要内容之一。实施小天体表面探测具有重要的科学与工程意义，对空间科学、行星科学、材料科学等领域的发展均有着促进作用［1］。迄今为止，各航天机构已实施了多项小天体探测任务，在这些任务中，有些探测器已经与小天体表面进行了接触或者向其投放了小型探测装置［2］。中国也以2016HO3 小行星及311P 彗星为目标推进小天体探测任务。相较于飞越和环绕探测，着陆探测无疑能够获得更全面和准确的小天体科学数据。

目前小天体着陆的主要难题在于其复杂弱引力环境以及未知的表面土壤性质，着陆器易发生反弹和逃逸。欧空局“罗塞塔”探测器释放的“菲莱”着陆器［3-4］接触到了67P 彗星的表面，但是锚定机构未能按计划展开，在表面发生了明显的翻滚弹跳。日本的“隼鸟”号［5］、“隼鸟”2号［6］以及美国的OSIRIS-REx 探测器［7］仅接触小天体表面进行采样，并未实现长时间的表面稳定着陆。为解决传统“刚性+缓冲”及“接触即走”着陆方式带来的不足，崔平远等［8］提出了柔性着陆的概念，文献［9］围绕该着陆方式对自主导航与制导控制等关键技术的研究进展与难点进行了总结和分析。如图1 所示，着陆器由质量聚集区（节点）及智能柔性材料两部分组成，通过增大与小天体表面的接触面积降低倾覆翻滚的风险，同时柔性材料可消耗着陆的残余动能，避免着陆器反弹逃逸。该着陆器具有节点间活动并行、约束耦合复杂、柔性干扰不确定等特点，因此着陆器需具备任务规划技术以提高其自主决策能力，实现复杂小天体环境下的安全着陆。

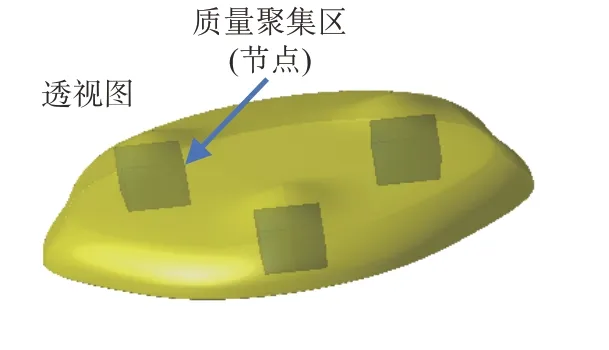
图1 柔性着陆器示意图Fig.1 Illustration of the flexible multi-node lander

相较于传统刚性着陆器，柔性连接的存在使得柔性着陆器活动间的时间约束更加严格、耦合。例如：t1，t2，t3分别为3 个节点的着陆时间约束，如图2所示，为满足柔性连接约束，在着陆整个过程中还需保证3个时间的相互差值在一定范围内。在柔性着陆器的规划过程中，每步规划均是在规划空间中搜索满足要求的活动来改变或扩展当前的部分规划，该过程的活动和时间约束信息是动态变化的。并且由于柔性连接约束不确定性的影响，节点的规划序列执行过程不是完全可控的，当执行出现偏差时，需要修复当前已有规划，对不确定性的干扰做出动态响应，快速确定规划修复后的活动执行区间，以提高着陆任务的安全性。因此，规划过程中时间约束推理的效率提升直接影响到规划速度。

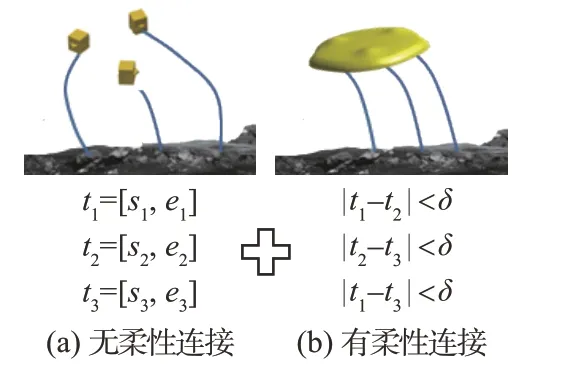
图2 时间约束耦合Fig.2 Temporal constraints coupling

时间约束推理是任务规划技术的重要组成部分，深空一号的远程智能体证明了自主任务规划问题中时间信息传播高效处理的重要性［10］。目前时间约束推理方法主要包括路径一致与弧一致两大类。Floyd-Warshall算法［11］可以计算时间约束网络中任意两个顶点间的最短路径，该方法约束传播次数多，计算效率较低。因此部分路径一致概念被应用于时间约束求解。ΔSTP 算法［12］以部分路径一致求解为核心，以存储资源为代价提高了计算效率，有效降低了约束推理次数。P3C 算法［13］采用有向路径一致（DPC），强制执行部分路径一致，进一步提高了时间约束推理效率。弧一致算法也通常被用于进行一致性判断，该类算法主要包括AC-1 到AC-7、AC-2000、AC-2001等［14］。Kong等［15］提出了ACSTP算法用以解决时间约束问题，在减少约束推理次数方面优于现有算法。美国火星探测车使用的MAPGEN［16］规划系统使用了基于弧一致的算法保证时间约束的一致，并保留了最大的时间灵活性。

但在动态的规划过程中，对于以上方法，每添加一个活动就需要对当前网络所有时间变量进行一次遍历计算，随着约束的增加，时间约束的计算量显著增加，从而影响到规划效率。针对这一问题，有学者提出了时间约束网络增量式维护方法。增量全路径一致（IFPC）算法［17］通过更新部分网络来维护全路径一致，增量部分路径一致（IPPC）算法［18］在添加新约束或收紧现有约束时保持部分路径一致性来维护当前网络。Xu等［19］提出时间约束几何分组动态推理（GDAC）算法，减少时间约束推理过程中的重复计算等。现有增量式方法大多以路径一致为基础，在计算过程中会额外增加新的约束，从而增加计算代价，基于弧一致的算法可有效避免这一缺陷。

本文针对小天体柔性着陆器着陆任务规划中的复杂时间约束推理问题，建立任务规划中的活动时间约束网络，进而划分约束类型，分析不同类型约束在时间网络中的传播特点，设计零点约束优先添加策略，减小规划过程中的时间约束传播范围。提出动态弧一致时间约束推理方法，局部求解时间约束网络一致性，获得着陆器系统可执行活动的最小可行区间。最后构建小天体着陆规划场景，从多方面验证了所提方法的有效性和高效性。

1 问题描述及模型建立

1.1 任务规划问题描述

本文主要研究小天体柔性着陆器着陆任务规划中的时间约束一致性推理问题。柔性着陆器着陆规划需要在复杂约束条件下求解每个系统待执行活动的可行起止时间。每个活动的时间信息可以由集合{s，d，e}来表示（s，d，e分别表示活动的开始时间、持续时间、结束时间），不同活动间存在复杂时间约束关系。例如：节点相机成像活动的开始时刻必须在姿态机动活动的结束时刻之后，并且每个节点的成像活动必须同时进行，以获得同时刻的图像用于着陆导航。首先描述柔性着陆器任务规划问题如下：

定义1.小天体着陆任务规划问题ΠA可采用如下元组表示：

式中：A为着陆器节点集合，Sa为节点包含的系统集合，Ox为系统可执行活动集合，Cx为活动的时间约束集合，Ix为系统初始状态，Gx为系统目标状态。

定义2.系统可执行活动oi∈Ox的时间信息可表示为如下元组：

式中：si为活动oi的开始时间点，ei为结束时间点，di为活动的持续时间，Ci为该活动与其他活动间的时间约束关系集合。

定义3.柔性着陆器着陆任务规划中的时间约束问题S=定义为一个一组有限时间点变量集合X={x1，x2，…，xn}和一组时间变量上的约束C={c1，c2，…，cm}。每个变量代表一个规划活动的开始或结束时间点，变量间的约束代表时间点之间的关系，对于定义在连续域上的时间点变量u，v∈X，其约束关系为一组线性不等式：

其中，a，b均为实数。

若存在时间变量赋值{x1=r1，x2=r2，…，xn=rn}满足所有约束，则当前规划活动的时间约束问题是一致的。

1.2 时间约束网络构建

为求解上述时间约束问题的一致性，并获得每个活动起止时间的最小可行区间，将该问题表示为加权有向图，也即时间约束网络G=。V为图的顶点集合，E为顶点间的边集合。时间变量u∈X表示为图中的顶点，变量间约束表示为边。

对于时间变量u，v，约束表示为区间Iuv=[a，b]，若u，v属于同一活动，则Iuv表示的是活动内部约束，即活动持续时长，若u，v属于不同活动，则Iuv表示活动间约束。如图3 所示，定义着陆任务执行的时间零点z，则活动的起止可执行时间为时间变量与时间零点间的约束关系，也即变量值域Iu=Izu，Iv=Izv。每个活动的开始时间点与结束时间点变量si，ei∈V，V={s1，e1，…，si，ei，…sn，en}∪{z}，n为当前部分规划中包含的活动数。变量间的时间约束表示为网络中顶点间的有向边权重，wsiei=bsiei，weisi=-asiei或Isiei=[-weisi，wsiei]=-Ieisi。

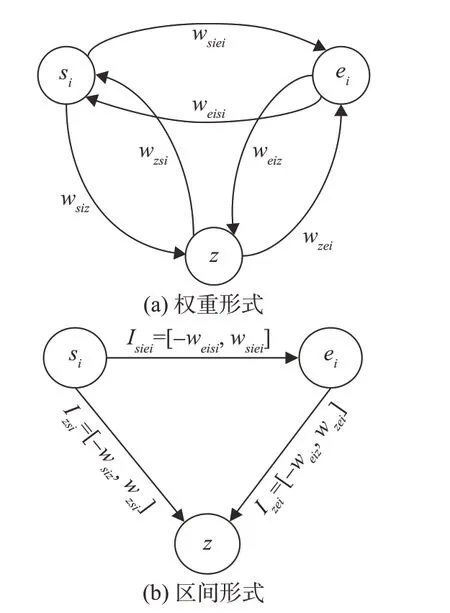
图3 时间约束网络示例Fig.3 Temporal constraint network example

根据变量间的时间约束关系进一步划分约束类型，如图4所示。As，Ae和Bs，Be分别表示活动A和活动B 的开始及结束时间点。其中，变量点与时间零点z间的约束称为零点约束（Cz），如IzAs=[8，11]表示活动A 的开始执行区间；同一活动的时间点变量间约束称为内部约束（CI），如IBsBe=[1.5，2]表示活动B 的可持续时间；不同活动的时间点变量间约束称为外部约束（CE），如IAsBs=)[1，∞表示活动B 至少在活动A 开始执行1 个单位时间之后再开始执行。从而时间约束网络G的边集表示为式（4），每条边(u，v)绑定约束类型Tuv，Tuv∈{Cz，CI，CE}。

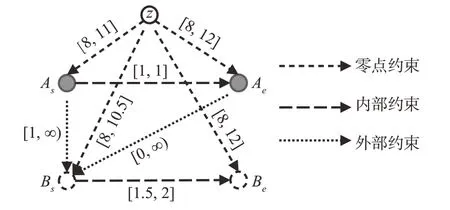
图4 约束类型划分Fig.4 Constraint type

对于定义在图G上的时间变量u，v∈V，存在路径u→v，其距离为Iuv。若存在时间变量j∈V，使得路径u→j→v有更短的距离，则更新Iuv。时间约束一致性推理的本质在于通过式（5）和（6）收紧原始约束，判断是否当前规划的所有活动约束都得到满足，并且求解当前网络中每个活动开始与结束的最小可行时间区间。

其中，运算符⊗定义为[a，b]⊗[c，d]≔[a+c，b+d]，并且[a，b]⊗∅≔∅，若存在=∅，则说明当前规划中活动的时间约束是不一致的，执行一次式（6）称为一次约束推理。

根据柔性着陆器每个系统的初始状态与目标状态初始化时间网络，随着规划活动的添加，逐步扩展网络规模并求解时间约束问题。

2 动态弧一致时间约束推理

柔性着陆器的规划过程中活动和时间约束都是动态变化的，约束信息的传播会影响当前已有规划活动的执行区间，若每次改变都对全局时间网络进行一次推理，则计算效率严重降低，本文提出一种动态弧一致时间约束推理方法，设计零点约束优先添加策略，根据添加的约束类型不同限制约束传播范围，仅对局部约束网络进行推理，减少规划中活动动态变化的影响范围，提高时间问题的求解效率。

2.1 时间网络弧一致

弧一致算法仅需求解每个变量值域的最小区间。也即，仅对变量与时间零点间的约束区间进行求交计算。

定义4.对于时间约束网络G=，u，v∈V，且值域分别为Iu，Iv，存在约束Iuv∈C。若对于任意tu∈Iu，存在tv∈Iv使得tv-tu∈Iuv，则Iuv相对于Iu和Iv是弧一致的。若对于任意约束Iuv∈C，Iuv和Ivu都是弧一致的，则约束网络G是弧一致的。

对于变量i∈V，构建其邻居变量集合Nei={j|(i，j)∈E}。弧一致算法在迭代中通过式（7）计算每个变量的新值域，若所有变量值域都计算完成后∃i∈V，且Ii≠，则继续下一次迭代，直到对于∀i∈V满足条件Ii=

2.2 约束添加策略

规划过程中的活动是逐步添加的，如图5所示，对于当前规划的待添加活动oi∈Ox，需要执行约束推理的时间网络包含两部分：当前部分规划中活动的时间变量和约束构建的原网络G0=以及待添加活动的时间变量和与G0中变量相关的局部约束网络Gp=。

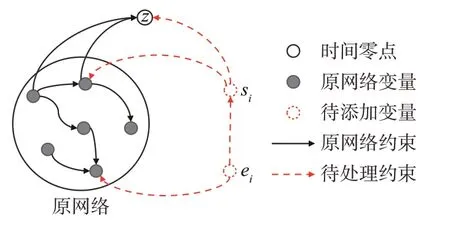
图5 待处理约束Fig.5 Pending constraints

为实现时间约束网络的局部动态维护，将活动oi相关的3 类约束逐条添加至原网络，从而对于每条新添加的约束而言，其对应的原网络=<>为G0与已添加至G0中的前序约束的并集。定义新添加约束的两个变量为u，v，边为euv，则该约束与G′0存在以下3类从属关系。

1)u，v∉且euv∉，该约束的添加不会对已有活动的时间可行区间造成影响，该情况下无需执行时间约束推理，约束推理次数为0。

2)u∈，v∉且euv∉，该情况有 两种可能，当Tuv=Cz时，时间变量v与中任意变量都不存在约束关系，因此该约束的添加不会影响中的时间区间，无需执行时间约束推理，约束推理次数为0；当Tuv=CI或Tuv=CE时，变量u的值域通过边euv传播，根据Iv=Iu⊗Iuv推理变量v的值域，约束推理次数为1。

3)u，v∈V′0，同样存在两种可能，当Tuv=Cz时，根据第二种情况的分析可知，由于该活动前序约束的添加，变量v的值域Iv已通过约束推理得出，此时∃euv∈。因此该约束首先与已有值域Iv进行求交计算，若计算后的值域=Iv，则该约束不影响G′0中的时间区间，约束推理次数为1；若⊂Iv，则该约束必定在网络中传播，推理变量v的邻居变量值域，若邻居变量值域也发生改变，则约束进一步传播，约束推理次数为式（8）。

当Tuv=CI或Tuv=CE时，需要分别计算变量u，v对互相值域的影响，进而根据区间减小与否执行约束传播，约束推理次数为式（9）。

根据上述3类从属关系下约束推理次数不同的分析可知，不同类型约束的添加顺序会影响约束的传播范围。对于活动oi∈Ox，根据定义的约束类型Tuv∈{Cz，CI，CE}，存在2 条零点约束、1 条内部约束及m条外部约束，有以下6种添加顺序，其约束推理次数分别为式（10）至式（15）。

1) 零点约束→内部约束→外部约束

2) 零点约束→外部约束→内部约束

3) 内部约束→零点约束→外部约束

4) 内部约束→外部约束→零点约束

5) 外部约束→零点约束→内部约束

6) 外部约束→内部约束→零点约束

其中，n0为活动oi添加前的时间约束网络中变量数；ax(x=0，1，…，m)表示第x条外部约束添加后值域发生改变的变量；b0，bin，均为布尔值，分别表示零点约束、内部约束及第j条外部约束添加后是否改变原网络中的变量值域，若发生改变，则为1，反之则为0(x=0，1，…，m)分别表示未添加内部约束和已添加内部约束时，第x条外部约束添加后第i个变量的邻居变量集合。

计算上述6 种添加顺序下的约束推理次数，易得式（16）。

对于r1，r2而言，分3种情况讨论：

1) 最小时间网络来自于内部约束传播，则外部约束的添加不会改变原网络中的变量值域，即=0，式（17）成立。

2) 最小时间网络来自于外部约束传播，则内部约束的添加不会改变原网络中的变量值域，即bin=0，式（18）成立。

3) 最小时间网络来自于零点约束，也即初始值域为最小值域，约束不传播，bin==0，式（19）成立。

内部约束与外部约束添加造成的约束传播范围与实际问题中的约束关系和约束数值有关，理论推导无法比较r1，r2的大小。因此，提出动态时间约束推理中的零点约束优先策略，以尽可能减小规划活动的约束传播范围，内部约束及外部约束可随机添加。针对柔性着陆器着陆任务，考虑规划过程中逐步添加的16个系统活动，包括96条约束。图6显示了6 种添加顺序下的约束推理次数曲线，进一步验证了所提策略的有效性。

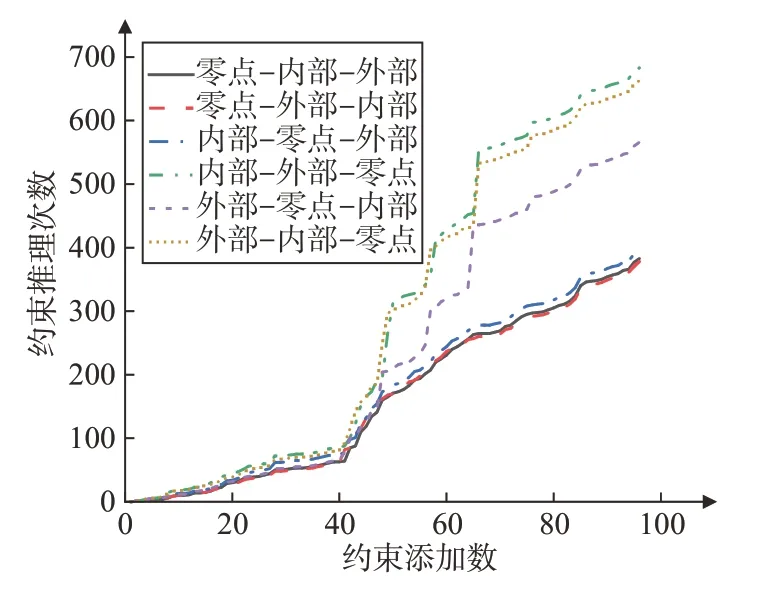
图6 6种添加顺序下的约束推理次数Fig.6 Number of constraint reasoning in six add orders

2.3 动态约束推理

综合上述分析及约束添加策略，根据新约束变量与原网络变量的从属关系以及新约束的类型，判断新约束在原网络中的传播范围，仅执行必要的局部约束传播，减少无效的一致性计算，有效降低约束推理次数，进而提出动态弧一致时间约束推理方法（DAC），逐步动态维护当前部分规划的时间约束网络一致性，并快速求解每个活动执行起止时间的最小可行区间，时间约束推理流程见图7，其中具体步骤如下：

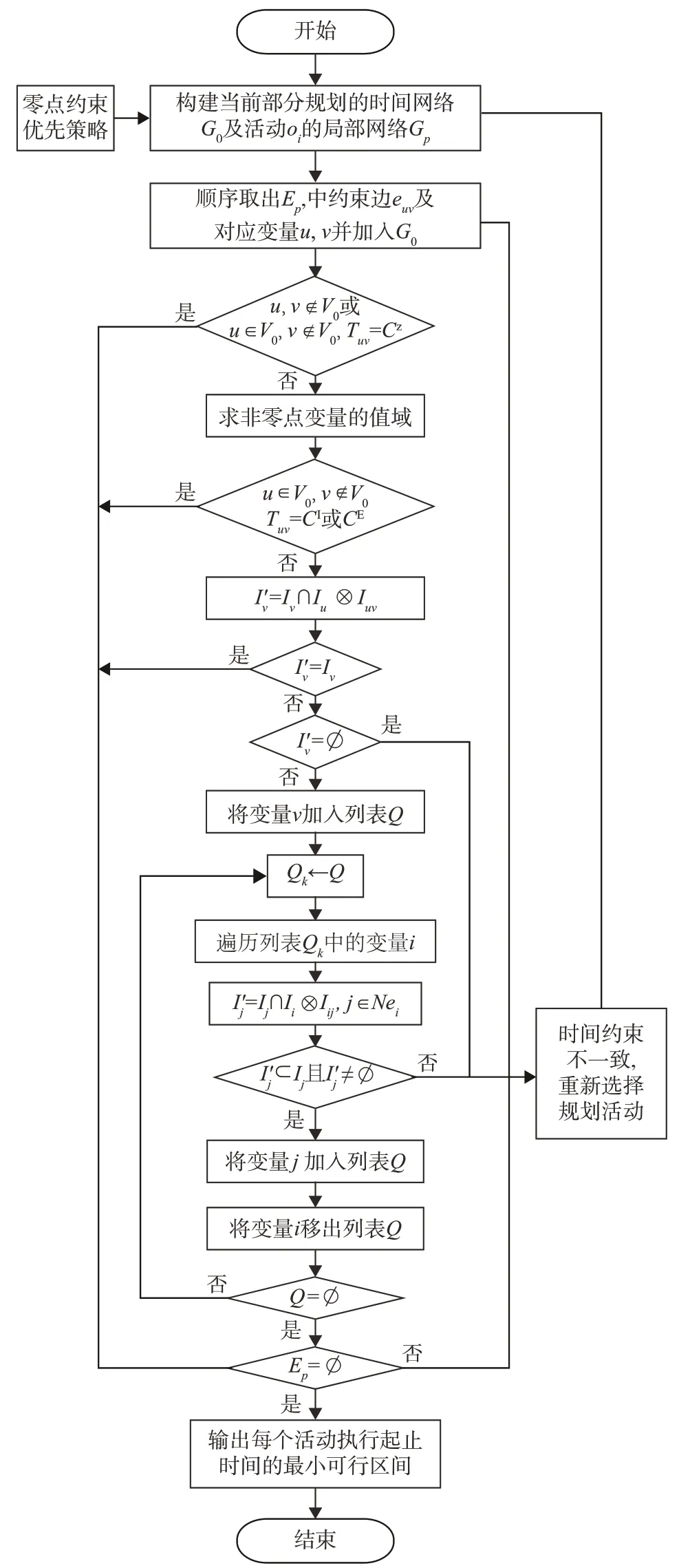
图7 动态弧一致算法流程图Fig.7 Flow chart of dynamic arc-consistent algorithm

1) 构建当前部分规划所包含活动的时间约束网络G0以及下一步规划待添加活动的局部网络Gp。

2) 按照零点约束优先策略生成待添加活动的约束集合，并顺序取出添加至约束网络G0。

3) 判断约束类型及变量与G0的从属关系，若u，v∉V0或u∈V0，v∉V0且Tuv=Cz，无需执行约束推理，执行步骤4；若u∈V0，v∉V0且Tuv=CI或CE，则计算变量v的值域，执行步骤4；若u，v∈V0，则执行步骤5。

4) 判断待处理约束集合是否为空，若为空则输出每个活动执行起止时间的最小可行区间，否则执行步骤2。

5) 首先求解新添加约束对其两个变量的值域影响（假设影响变量v），若=∅，说明变量v不存在取值满足当前规划的时间约束，也即时间约束不一致，则执步骤7；若=Iv，说明当前添加的约束不会影响变量v的时间区间，无需进一步推理，执行步骤4；若⊂Iv且≠∅，则该约束在网络中传播，将变量v加入变量值域更新列表Q，并执行步骤6。

6) 通过列表Q对约束传播进行判断，计算新约束影响范围内的变量值域，判断变量计算后值域削减与否来限制约束传播，缩小约束传播范围，减少时间约束推理次数，节省着陆器有限的计算资源，提高复杂时间约束推理效率。将Q赋值给列表Qk，遍历所有变量i∈Qk，计算值域Ii对所有邻居变量值域Ij，j∈Nei的影响，若Ij=∅，则时间约束不一致，执行步骤7；若I′j⊂Ij且Ij≠∅，约束继续传播，将变量j加入Q。当集合Nei遍历完成后，将变量i移出集合Q并判断Q是否为空，若Q=∅，约束传播结束，所有变量的值域都已计算至最小，执行步骤4；若Q≠∅，Q中变量值域继续传播，重新执行步骤6。

7) 重新进行规划搜索选取合适的活动，执行步骤1。

该方法以网络弧一致为基础，通过对规划过程中待添加活动的时间约束类型划分以及零点约束优先添加策略，在推理过程中无需增加额外的网络边，同时尽可能限制约束的传播范围，减少规划中时间约束推理耗时，有效提高柔性约束下柔性着陆器着陆任务规划的实时性。

3 仿真实验

3.1 场景设计

为了说明所提DAC 方法的效果，设计柔性着陆器着陆任务进行仿真。着陆器包含3 个节点，每个节点包含若干分系统。以规划中的成像系统为例，每个节点均携带光学相机，在着陆器着陆过程中获取小天体表面信息，提取规划问题中3 个相机的成像准备和成像工作两个活动，其初始时间约束关系如图8 所示，图中xs，xe分别表示活动x的开始时间点与结束时间点变量，其余类推。

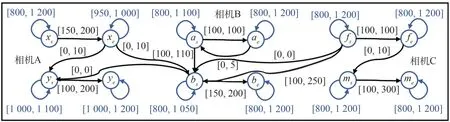
图8 三个相机的活动时间约束Fig.8 Temporal constraints of three cameras’ activities

随着规划搜索的进行，在成像系统的部分规划中动态添加上述两个活动，并进行时间约束网络的一致性判断，求解每个活动执行起止时间的最小可行区间，部分规划活动的甘特图如图9所示，满足相机A、B 同时开始工作的约束，活动的最小可行区间如图10所示，结果证明了DAC方法的有效性。

为进一步证明DAC 算法对于柔性着陆器在不同任务场景下的适应性，以公开的时间网络数据集为基础［20］，设计着陆器着陆任务规划中活动间时间约束关系数值，分3种不同情况进行仿真对比，多方面验证DAC 算法效率，从而体现DAC 算法的动态性能。

情况一：验证规划过程中新添加的活动数对时间约束推理效率的影响。活动数体现了着陆任务的复杂度，着陆器在相同目标状态下改变着陆过程中各系统所需执行的任务，并生成具有不同活动数和不同约束数的数据集，如表1所示。

情况二：验证系统间时间约束耦合程度对时间约束推理效率的影响。假设着陆器节点总共具有16 个系统，每个系统具有10 个不同的可执行活动，对于同一着陆任务，改变系统间的约束数，如表2所示。

表2 系统间约束数Table 2 Number of inter-system constraints

情况三：验证着陆器节点不同系统组成对时间约束推理效率的影响。每个系统同样具有10个可执行活动，改变单个节点包含的系统数，系统间约束数M与系统数N满足关系M=50(N-1)。如表3所示。

表3 单节点包含的系统数Table 3 Number of systems contained in a single node

3.2 对比分析

为了验证时间约束推理方法的高效性，本节将所提的DAC 算法与NASA 建立的EUROPA 规划器中采用的动态适应单源最短路径时间约束推理算法（ABF）［20］进行比较。

如图11所示，当规划过程中新添加活动数不同时，DAC 算法相较EUROPA 算法，运行时间平均减少90.7%，且随着活动数的增加，差距进一步增大，DAC 算法耗时增长更慢。图12 显示了108 个活动下每条约束添加至原网络中时，执行约束推理所需的时间，虚线表示单条约束平均推理时间，实线表示单条约束推理时间的标准差，DAC 算法效率显著提高，且算法稳定性更好。

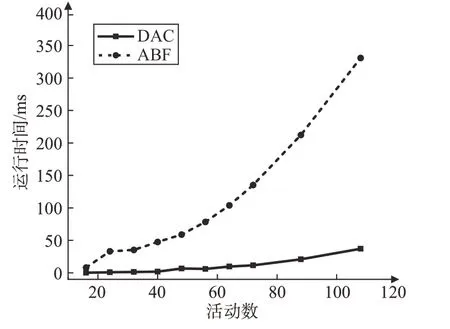
图11 不同活动数的算法运行时间Fig.11 Running time of the algorithms with different number of activities

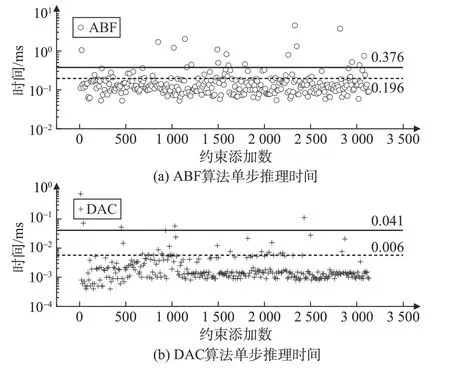
图12 单步约束推理时间（108个活动）Fig.12 Single-step constraint reasoning time（108 activities）

对于不同系统间约束数，DAC 算法平均效率提高78.8%，如图13 所示。当系统数不同时，DAC算法效率依然占优，平均提高78.5%，且随着系统数的增多，优势更加明显，如图14所示。柔性着陆器相较于传统单体着陆器具有系统多、约束耦合强、规划活动多的特点，因此，DAC算法能够更好地适应柔性着陆器着陆任务，提高任务规划过程中的时间约束推理效率，进而增强着陆器着陆任务规划的实时性。

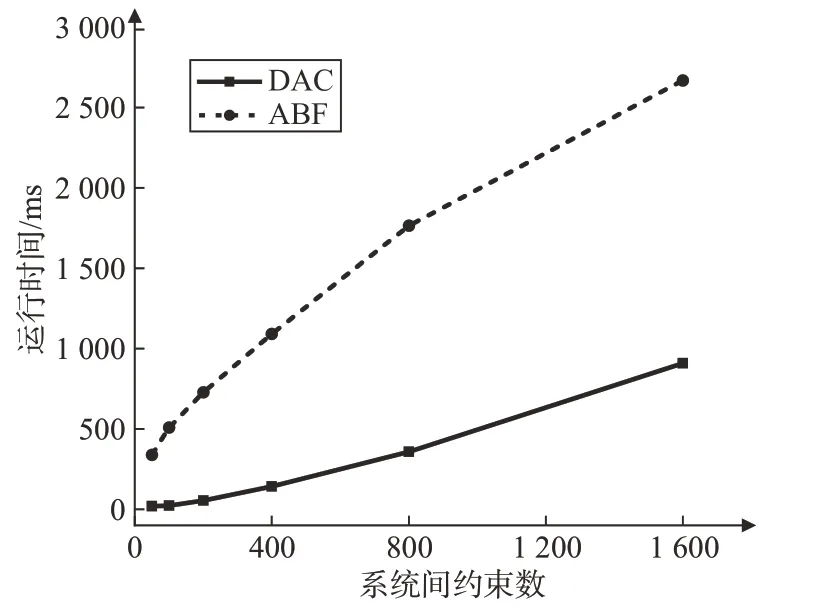
图13 不同约束数的算法运行时间Fig.13 Running time of the algorithms with different number of constraints

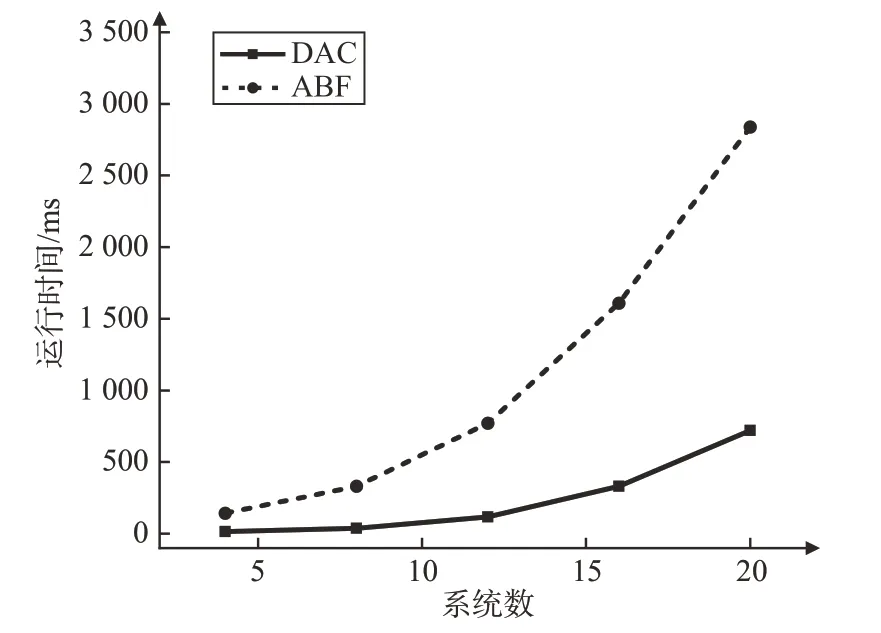
图14 不同系统数的算法运行时间Fig.14 Running time of the algorithms with different number of systems

4 结论

本文针对小天体柔性着陆器的复杂时间约束推理问题，提出动态弧一致时间约束推理方法。提取规划活动的时间约束信息，构建部分规划与待添加活动的时间约束网络；分析活动约束与时间网络的从属关系，避免无效推理；设计了零点约束优先添加策略，进一步减小时间约束的传播范围，从而实现规划过程中动态活动添加的局部时间约束推理，提高了约束推理效率。本文提出的方法能够快速判断时间约束一致性并求解规划活动可执行的最小可行区间，可为提高柔性着陆器着陆任务规划的实时性、增强着陆器自主决策能力提供技术支持。