基于拍卖鸽群优化算法的多无人机追踪分布式任务分配

胡超芳，宋思涵，徐嘉均，王迪迪

基于拍卖鸽群优化算法的多无人机追踪分布式任务分配

胡超芳，宋思涵，徐嘉均，王迪迪

(天津大学电气自动化与信息工程学院，天津 300072)

无人机技术已经广泛应用于各种研究领域，任务分配是多无人机协同的关键技术之一，对多无人机任务完成质量的影响极大，针对多个目标追踪场景下的多无人机任务分配问题，提出了一种基于拍卖鸽群优化(auction-PIO)算法的分布式分配方法．首先采用追踪总距离、分配均衡性、任务完成时间3个性能指标，结合追踪任务约束条件，建立了分布式多指标0/1整数规划模型．然后以拍卖策略作为分布式优化框架，无人机作为拍卖者对地面目标进行竞拍出价，通过多轮竞拍确定任务分配方案．为提高拍卖分配的最优性，增强了各无人机间的共享信息量，进而使无人机可对所有目标进行竞拍出价，并引入PIO算法更新各无人机的竞拍价格，将鸽子位置编码为无人机对各地面目标的竞拍增价，利用地图指南针算子和地标算子迭代更新种群位置，实现对无人机竞拍价格的优化更新．在此基础上，设计基于目标优先级的解算策略，用于将竞价矩阵和距离矩阵解算为任务分配方案，并进行了算法的计算复杂度分析．最后对所提拍卖鸽群优化算法分别进行了数值仿真、Gazebo虚拟仿真和实机户外飞行实验，结果表明：所提算法拥有良好的任务分配性能，不但在数值仿真对比中，优化性能比经典拍卖算法提高了12.16%，而且虚拟仿真和户外实验也说明算法能够满足实用性要求.

无人机；目标追踪；任务分配；拍卖；鸽群优化

近些年，无人机技术广泛应用于各个研究领域，人们对无人机完成复杂任务的需求不断增长[1]．其中，无人机追踪地面目标是一个热点研究方向，但是单架无人机执行追踪任务存在覆盖范围有限、容错性低等局限性．因此许多学者对多无人机协作进行大量的研究，其中作为多机协同的一大关键技术，任务分配得到了广泛关注[2]．

多无人机任务分配问题是指考虑多无人机有限资源约束，以整体任务效果最优为目标，将各具体任务分配给不同无人机．其分配执行策略主要包括集中式和分布式两种，其中集中式分配是将所有无人机信息汇聚在一个控制中心进行分配计算的，分配方法分为最优化方法[3]和启发式方法[4]．最优化的方法是找到任务分配问题的最优解，然而当问题规模增大时，最优化方法的求解复杂度急剧升高．启发式算法追求计算时间与求解精度之间的平衡，集中式任务分配大多用启发式算法，如遗传算法[5]、蚁群算法等[6].但是集中式分配难以摆脱计算量大、依赖处理中心 等局限，因此分布式算法成为任务分配领域的研究 热点.

在分布式的框架下，各无人机独立获取信息并进行决策，拥有较好的实时性和鲁棒性．常见的分布式任务分配算法包括基于博弈论的任务分配[7]、基于群体行为激励的任务分配[8]、基于市场竞拍机制的任务分配[9-10]．其中，基于博弈论的任务分配方法针对多无人机间任务执行的相互依存性，引入了博弈论思想使多个无人机互相竞争协商，从而得到较优任务分配结果．该方法采用隐式通信模式，系统通信负载小，但因其分配结果由规则设定，很大程度上与阈值的选择有关，较难保证分配效果．基于群体行为激励的任务分配方法将无人机感知环境信息映射到无人机行为模式的改变，实现全局任务分配方案的自动调整．该方法通信量较小、速度快，具有一定鲁棒性，仅适用于解决个体行为较为简单的多智能体系统．市场机制是模拟市场竞价、竞拍过程的一种分布式策 略[11]，其本质是各个智能体追求自身收益最大，在某种协议的限定下与其他智能体对话协商，从而动态实现任务分配．基于市场机制具有适中的计算成本和通信负载，求解效率高，适合进行实时任务分配，近些年受到了广泛的关注与研究．

分布式拍卖算法是一种常用的基于市场机制的任务分配方法[12]．对于多无人机任务分配而言，各无人机通常作为拍卖者，对最感兴趣的任务进行出价，出价最高的无人机获得任务，未竞拍成功的无人机可以继续提高报价进行竞争，直到各无人机都获得最大收益，其中竞拍价更新策略的设计极大地影响算法性能[13]．经典拍卖算法的竞拍价更新原则是最大净利润与第2大净利润之差，由于对信息的利用有限，仅能优化单一指标[9]．Lee等[14]为了保证机器人的任务完成可靠性，将多种有限资源作为确定拍卖价格的影响因素，提出了面向资源的分散拍卖算法．该算法求解速度快，然而只考虑有限资源而不重视任务收益，在其他场景并不适用．Braquet等[15]为了获得最佳评估的竞拍价向量，将其定义为系统总效益与缺少一个智能体的系统总效益之差．该定义虽然可以获取最佳评估的竞拍价向量，但计算量难以控制，且在某些场景中系统总效益很难确定．由此可见，竞拍价格更新策略的设计存在求解精度与计算量之间的矛盾．群体智能算法近些年常常被应用于解决优化问题，鸽群优化(PIO)算法相较于其他群体智能算法有更好的收敛性和求解精度[16]，已广泛应用于各种连续优化问题[17-18]，因此鸽群优化算法拥有应用于拍卖算法中竞拍价更新的潜质，种群编码和个体位置的评价策略是鸽群优化算法应用的关键．

本文针对多个目标追踪场景下的多无人机任务分配问题[19]展开研究．首先提出了追踪总距离、任务分配均衡性、任务完成时间3个性能指标，综合每个目标至少有一架无人机追踪，每架无人机只能追踪一个目标的约束条件，构建了分布式多指标0/1整数规划模型．在求解算法设计方面，以拍卖策略作为分布式实现框架并进行了改进．为了提高拍卖优化的最优性，各无人机共享更多信息，即不再只对单一目标进行出价，而是对所有目标均给出报价．此外，考虑基于规则式的竞拍价更新策略存在求解精度与计算量之间的矛盾，鉴于鸽群优化算法在处理该矛盾上的优势，采用鸽群优化算法对竞拍价进行优化更新. 鸽群位置编码与评价成为鸽群优化算法在拍卖策略中应用的关键问题．本文将鸽群位置编码为竞拍增价，并设计了一种基于目标优先级的任务分配方案解算策略，将无人机竞价信息解算为任务分配方案，用于鸽群优化算法的个体位置评价．最后，通过与经典拍卖算法进行的数值仿真对比，优化性能提高了12.16%，验证了本文方法的有效性，并将其移植到Gazebo仿真环境和多无人机协同追踪实验系统，进行了虚拟仿真与实机飞行测试，进一步验证了本文方法的实用性．

1 多无人机追踪任务分配建模

1.1 问题描述

以城市环境为具体应用背景，多架无人机追踪多个地面目标问题如图1所示，通过任务分配，各无人机明确需要追踪的目标，并尽可能靠近所跟踪的目标，使目标时刻处于无人机视野范围内．本文以图1中的虚线表示任务匹配关系，做出如下假设：

(1) 无人机是同构的，飞行速度相同；

(2) 每个目标的追踪需求相同，即每一架无人机可以追踪任意一个目标，每个目标可以被任意一架无人机追踪；

(3) 地面目标的位置和移动是已知的．

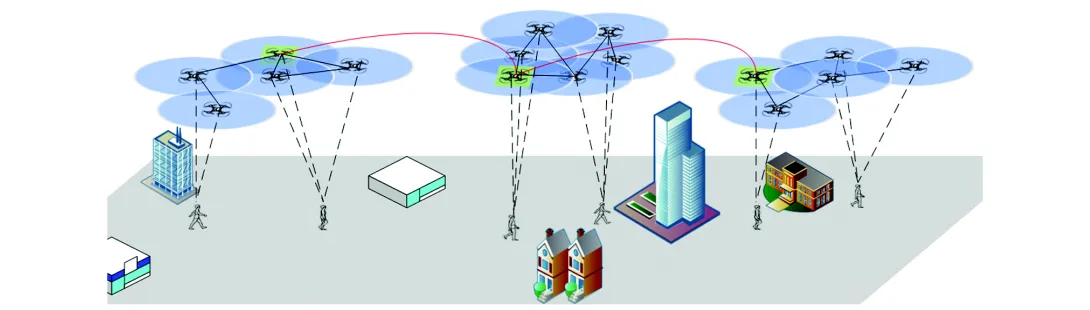
图1 追踪场景多无人机任务分配示意

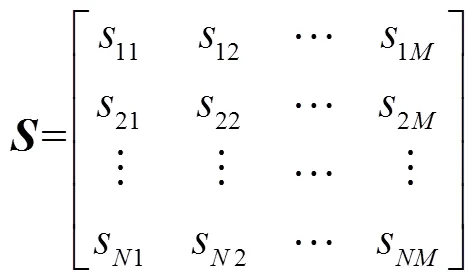
假设各无人机、目标定位精确，即各无人机内存储的距离矩阵相同．

1.2 约束条件

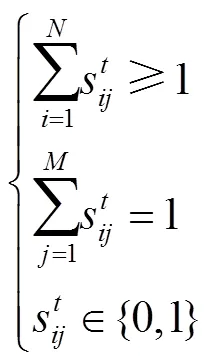
1.3 性能指标

针对多个目标追踪任务，本文主要从追踪效果、节约能源等角度，采用以下性能指标.

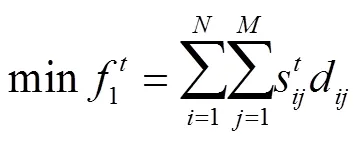
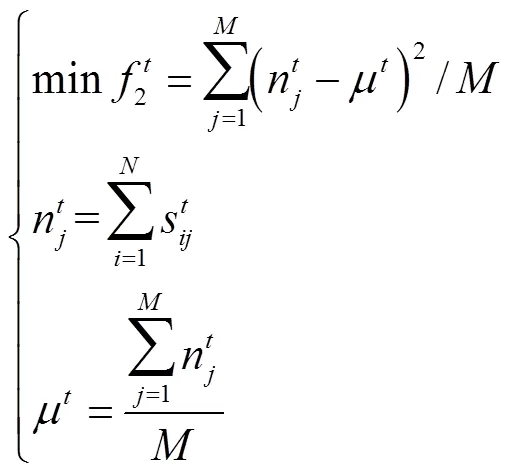
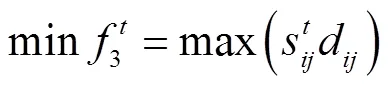
1.4 分布式多指标任务分配模型

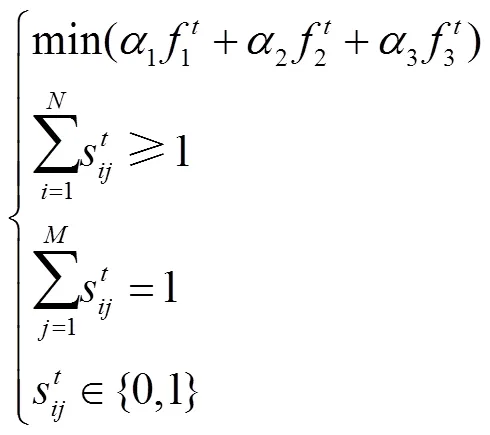
2 拍卖鸽群优化算法

2.1 分布式拍卖框架

本文将拍卖思想运用于多无人机追踪任务分配，将无人机作为竞拍者，地面目标作为竞拍物品．各无人机互相共享信息，实时调整自身的竞拍价格，最终通过多轮竞拍敲定任务分配方案．本文假定无人系统已构成通信网络，各无人机能够通过信息共享获取全局信息．

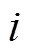
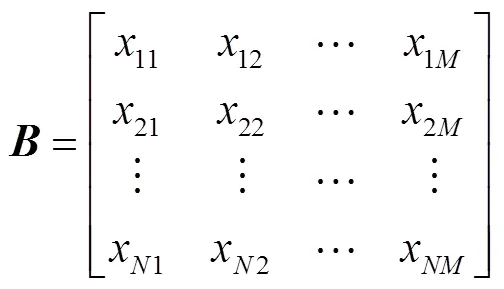
各无人机需要根据当前信息对自身的竞拍价格进行优化更新，并重新共享给其他无人机，进行下一轮竞拍．

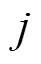
然而经典拍卖算法的竞拍价更新规则仅考虑无人机自身的利益最大，在实际的大规模任务分配问题中，还对整体指标有相应的要求，例如本文提出的任务分配均衡性、任务完成时间，直接应用经典拍卖算法的竞拍价格更新原则无法获得良好的任务分配效果，因此在后续算法设计中，本文引入了鸽群优化算法进行各无人机竞拍价格的更新．

在各无人机共享信息并更新竞价矩阵后，需要结合距离矩阵解算出任务分配方案，并与上一轮获得的任务分配方案进行比较，若相同则判定算法收敛，否则继续进行拍卖优化．为了保证算法速度，以及解算得到的任务分配方案满足追踪场景下的约束条件式(3)，本文设计了一种基于目标优先级的任务分配方案解算策略，该策略同时也应用于鸽群优化算法的种群评价环节．

2.2 基于目标优先级的任务分配方案解算

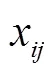
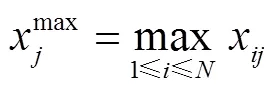
式中avg表示具有最高竞拍价的无人机．

差值计算式为

定义目标优先级指数为

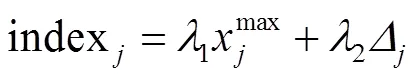
步骤1 对每个目标使用式(13)计算目标指数优先级指数，并根据目标指数优先级指数进行排序，获得目标分配顺序．

步骤2 各目标按照顺序进行任务分配，优先分配给出价最高的无人机．

步骤5 判断是否所有目标都已分配，若有目标未进行分配，则返回步骤2．

步骤6 未分配的无人机选择距离最近的目标进行辅助追踪.

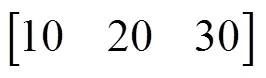
2.3 基于鸽群优化算法的竞拍价更新策略

2.3.1 鸽群优化算法

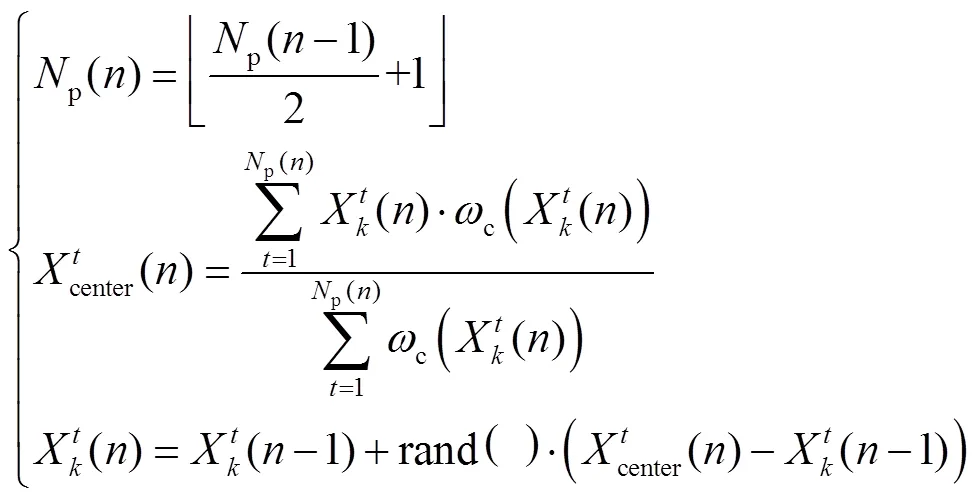
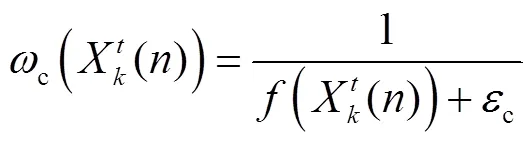
2.3.2 鸽群位置评价

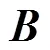
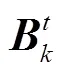
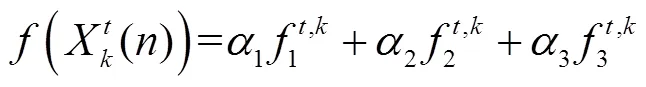
2.3.3 鸽群优化算法更新竞拍价流程

使用鸽群优化算法更新各无人机的竞拍价过程伪代码如下所示.

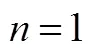
鸽群位置编码为无人机对各目标的竞拍增价，初始化鸽群位置；

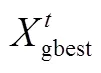
end while

使用地标算子式(15)更新鸽群位置；

end while．

2.4 拍卖鸽群优化算法流程

步骤1 向其他无人机发送自己的位置和初始竞拍价，接收其他无人机发送的位置和初始竞拍价．

步骤3 鸽群位置编码为该无人机对各目标的竞拍增价，并利用鸽群优化算法优化该无人机对各目标的竞拍增价．

步骤4 向其余无人机发送更新后的竞拍价，并接收其余无人机发送的新竞拍价．

步骤5 更新竞价矩阵，并使用基于目标优先级的任务分配方案解算策略解算出任务分配方案．

步骤6 与上一次任务分配方案对比，若一致则输出任务分配结果，否则返回步骤3．

2.5 算法复杂度分析

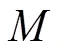
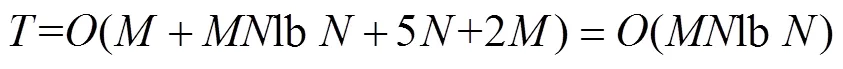
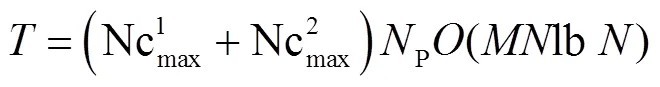
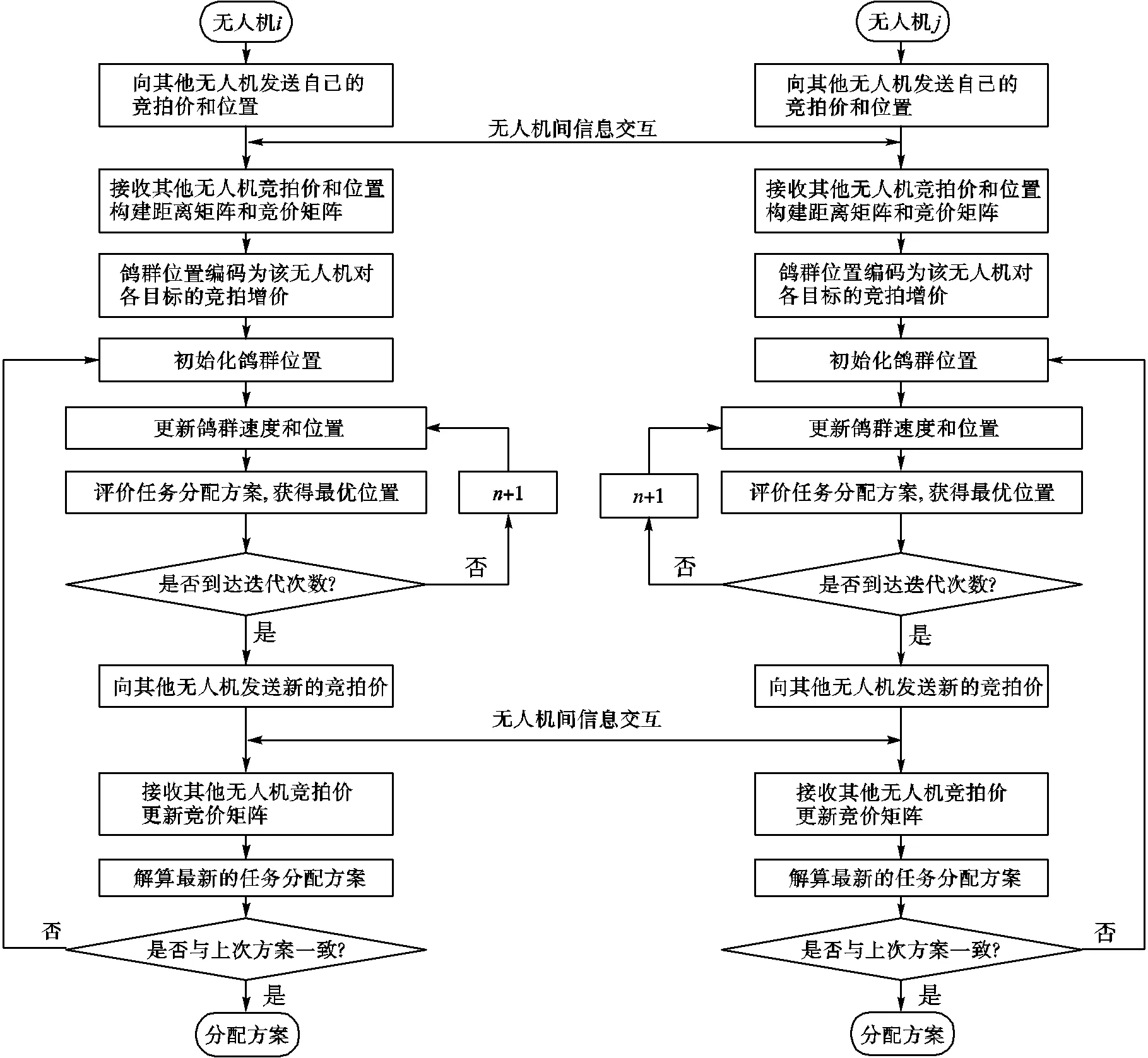
图2 基于拍卖鸽群优化算法的任务分配流程

3 仿真和实验验证

本文对所提算法进行了数值仿真、Gazebo虚拟仿真和实机飞行实验，进而验证了其性能和可行性．

3.1 数值仿真

3.1.1 静态任务分配验证

采用随机分布在非建筑位置上的50架无人机与35个地面目标对静态任务分配进行测试，图4和图5分别展示了使用本文提出的拍卖鸽群优化算法和经典拍卖算法的静态任务分配效果．其中品红色三角形表示无人机，蓝色的圆形表示地面目标，绿色的连线表示无人机追踪目标的匹配关系，两种方法均能获得可行的任务分配方案．在图中，红色的加粗直线和圆圈表示本文所提方法任务分配方案优于经典拍卖算法任务分配方案的例子．可以看出经典拍卖算法容易出现过长距离的追踪，这会导致整体任务完成时间延长，同时也会出现5架无人机追踪同一目标的任务分配不均的状况，而本文所提方法可以获得更加理想的任务分配结果．

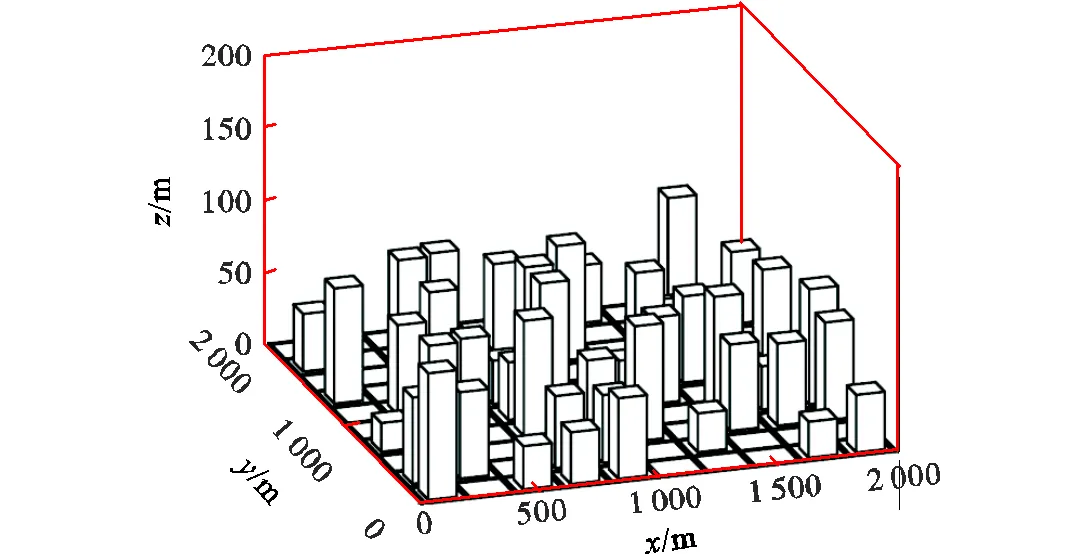
图3 数值仿真地图

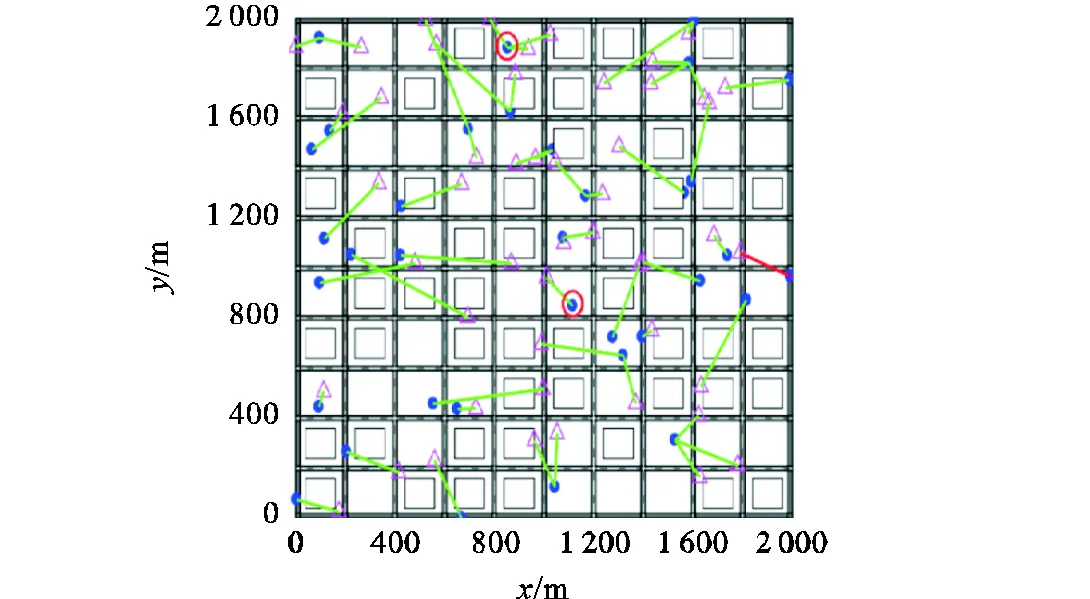
图4 基于本文所提算法的任务分配结果

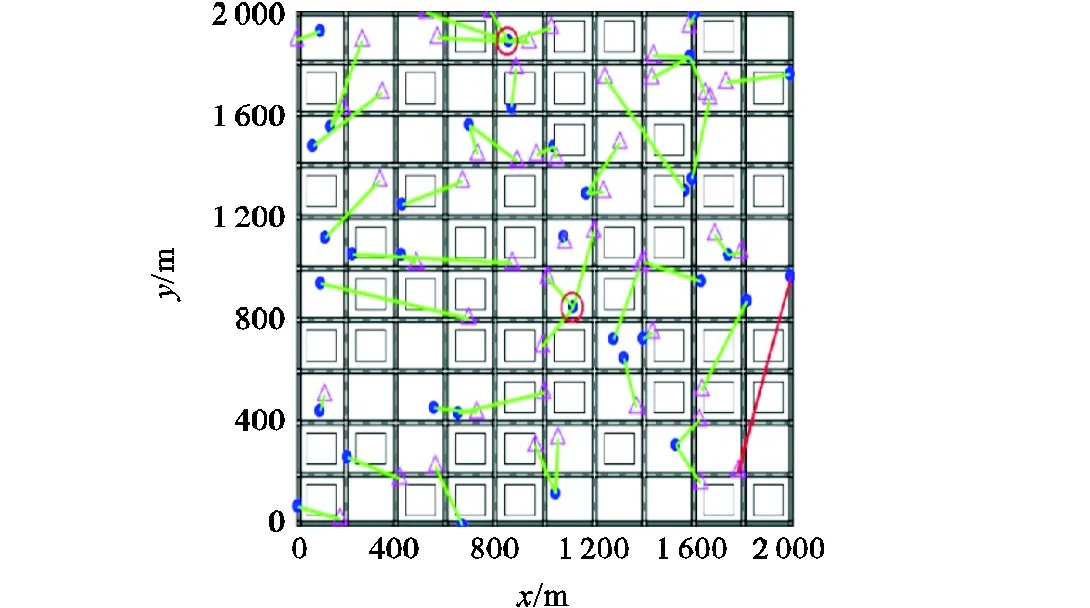
图5 基于经典拍卖算法的任务分配结果

图6(a)～(c)展示了各性能指标在迭代过程中的变化过程，均保持着下降趋势，个别指标出现暂时上升是为了对其他性能指标进行优化，由图6(d)可以看出在迭代过程中，加权性能指标持续优化下降．表1展示了所提算法与经典拍卖算法的优化结果性能指标对比，由表1可知，所提方法的所有性能指标均优于经典拍卖算法，尤其是在任务分配均衡性和最大追踪距离方面，总体优化性能相较于经典拍卖算法提高了12.16%．

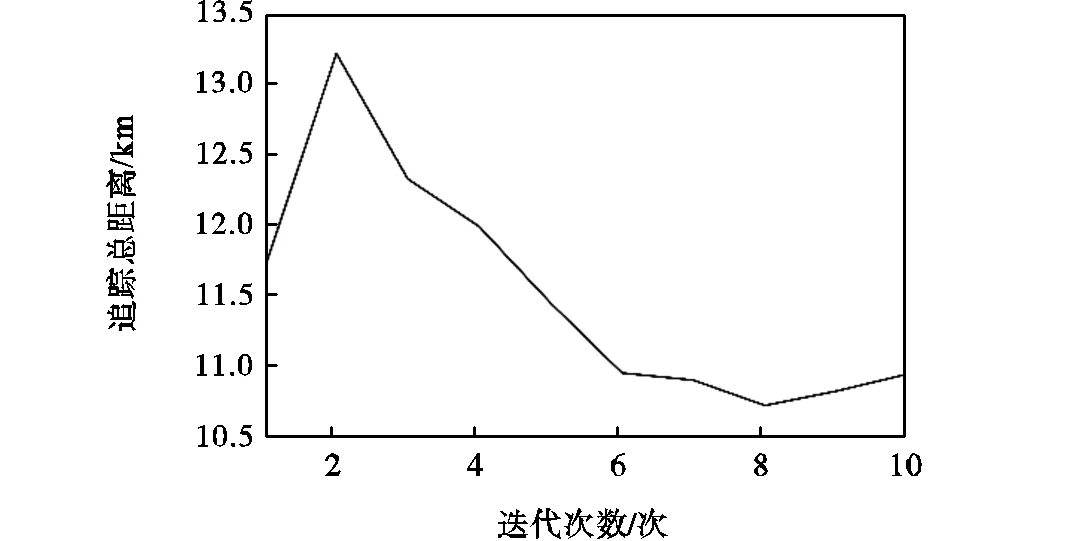
（a）追踪总距离

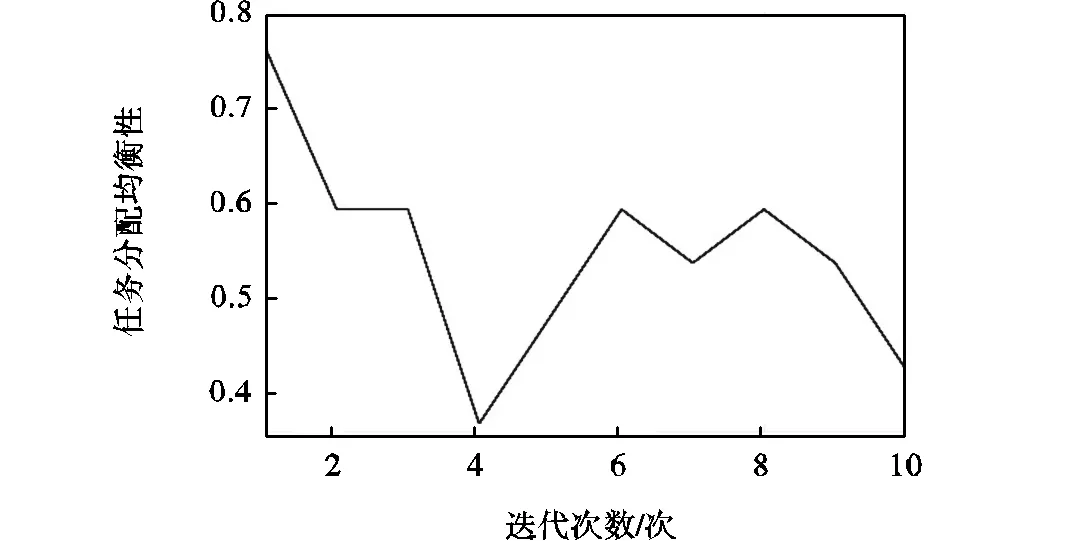
（b）分配均衡性

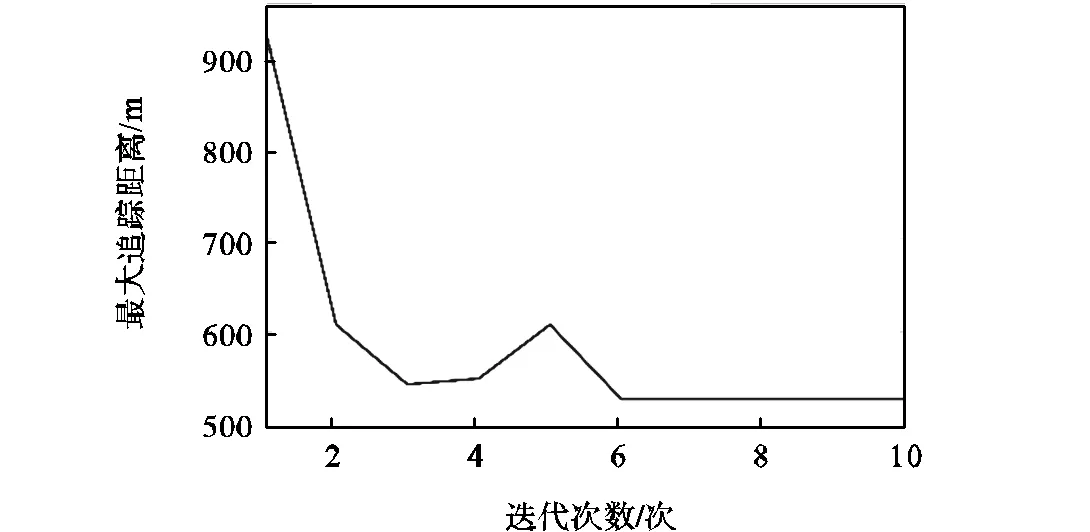
（c）最大追踪距离

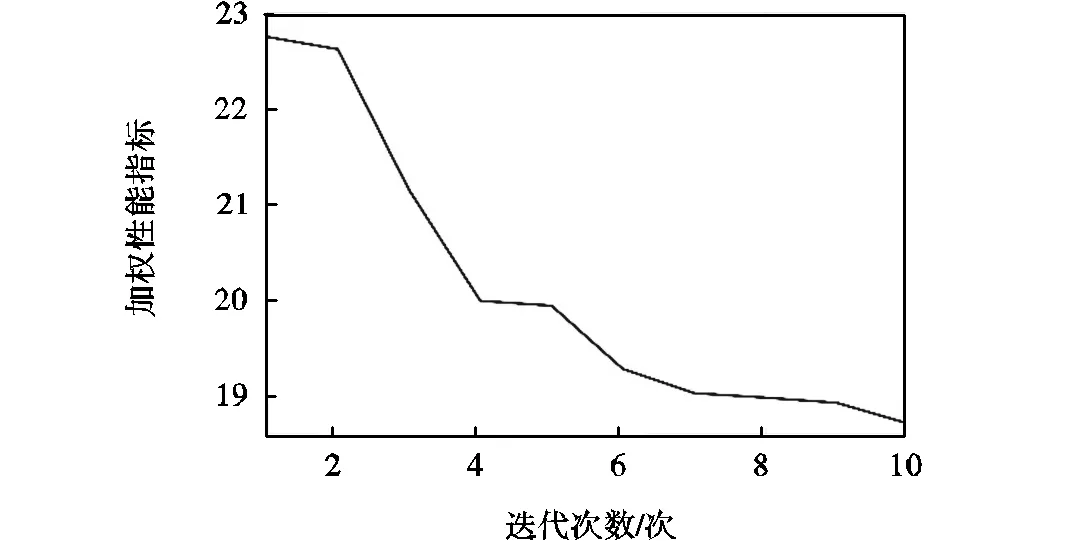
（d）加权性能指标

图6 拍卖鸽群优化算法优化曲线

Fig.6 Optimization curves of the auction-PIO algorithm

表1 2种算法优化结果对比

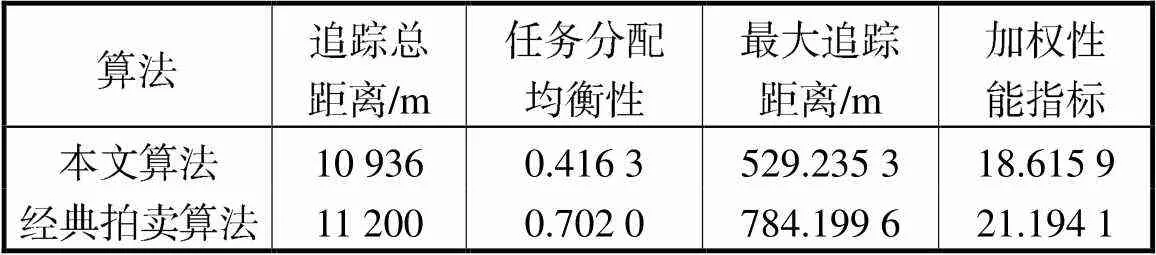
Tab.1 Comparison results of the two algorithms

3.1.2 动态任务分配验证

动态任务分配验证中，为了保证结果的清晰和直观，无人机数量为9架，地面目标数量为5个．无人机以7.5m/s的速度做匀速运动，地面目标以5m/s的速度做匀速运动，运动轨迹如图7所示，无人机使用本文所提方法进行任务分配，并根据航迹规划计算出的航迹对地面目标进行追踪．追踪效果如图7所示，其中蓝色圆形连成的曲线代表地面目标的运动轨迹，品红色的三角形表示无人机飞行的航点，较大的圆形和三角形为地面目标和无人机的初始位置，所有目标均受到了较好的追踪．此外，在无人机飞行过程中，由于受到任务分配算法的控制，共有两架飞机的追踪任务发生了改变，如图8所示，时间先后顺序为(a)～(d)．可以看出，本文所提的任务分配算法能够为无人机选择最佳任务，提高追踪任务完成效率．

图7 多无人机追踪过程

（a）时刻1    （b）时刻2

（c）时刻3    （d）时刻4

图8 不同时刻的任务分配结果

Fig.8 Task allocation results at different moments

3.2 Gazebo虚拟仿真

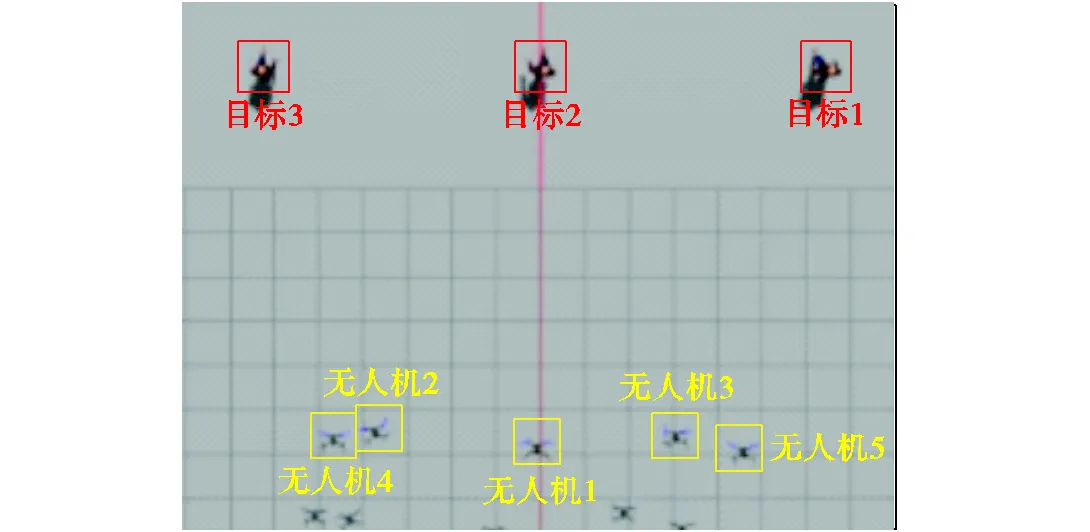
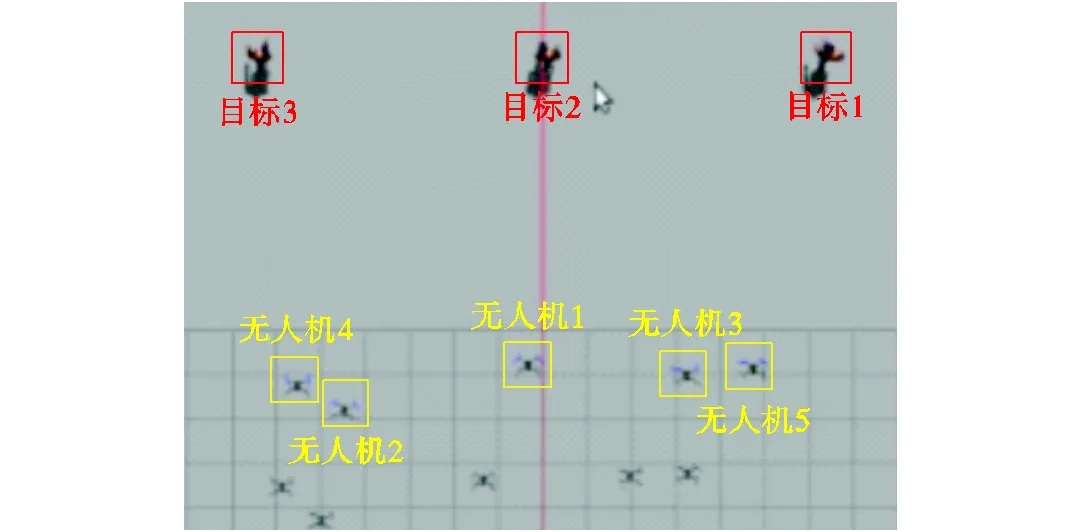
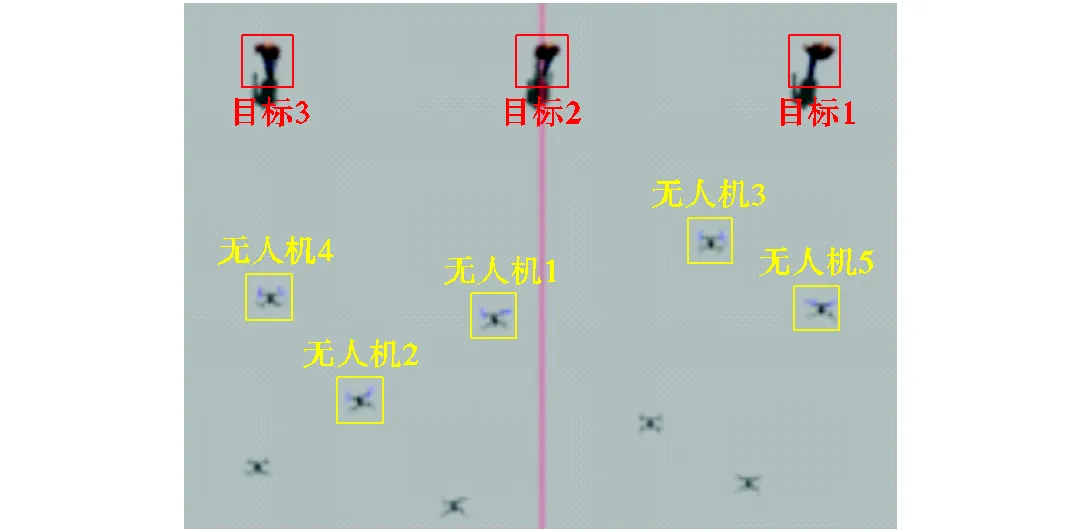
仿真环境中设置5架无人机和3个地面运动行人，5架无人机间隔2m呈一字形排列．行人的速度设置为1m/s．仿真的追踪过程如图9所示，算法得到的任务分配方案如图9(a)所示，并绘制出无人机和地面目标的运动轨迹如图10所示，多无人机可以通过本文算法解算出合理的追踪任务分配方案．图11展示了拍卖鸽群优化算法迭代过程中的加权性能指标的变化曲线，共迭代5次达到最优，任务分配方案解算时间不超过0.5s，满足追踪系统性能需求．

（a）时刻1

（b）时刻2

（c）时刻3

（d）时刻4

图9 Gazebo虚拟仿真追踪过程

Fig.9 Tracking in Gazebo virtual simulation

图10 无人机与地面目标运动轨迹

图11 虚拟仿真中拍卖鸽群优化算法迭代优化曲线

3.3 实机户外实验验证

多无人机协同追踪实验系统由5架无人机及配套设备构成，无人机间利用局域网进行ROS话题的订阅和发布，实现位置、竞拍价格的共享．无人机使用机载计算机进行上层控制，运行任务所提分配算法和已有的航迹规划算法，任务分配算法负责选择待追踪目标并将其位置发送到航迹规划算法，规划的航迹通过串口通信传递给成熟的底层飞控进行无人机位置控制．实验系统通过差分GPS获取无人机精确定位信息，为了充分验证分配算法的性能，本文通过UWB局部定位系统来获取地面目标精确定位信息．将经过虚拟仿真验证的程序移植到多无人机协同追踪实验系统，算法参数同Gazebo虚拟仿真保持一致．

实验布置与仿真中保持一致，实验过程如图12所示．使用本文提出的任务分配算法获得到的匹配关系如图12(a)所示．以无人机1上电位置为坐标原点，绘制5架无人机和3个地面目标的运动轨迹，图13为三维运动轨迹效果，图14为俯视二维运动轨迹效果，其中彩色线条表示无人机的运动轨迹，黑色线条表示地面目标的运动轨迹，无人机系统能够对地面目标进行较好的追踪．算法迭代过程中加权性能指标变化曲线如图15所示，3次迭代后达到最优，总用时小于0.3s，任务分配算法速度满足实验系统需求．在本文的研究中，动力学约束由已有的航迹规划和底层控制满足．实验结果表明：在具备有效的航迹规划和底层控制方法的基础上，通过本文所提算法可以快速解算出合理的任务分配方案并实现多无人机追踪多个地面目标．

（a）时刻1

（b）时刻2

（c）时刻3

（d）时刻4

图12 户外任务分配实验过程

Fig.12 Process of outdoor task allocation experiment

图13 三维无人机与地面目标运动轨迹

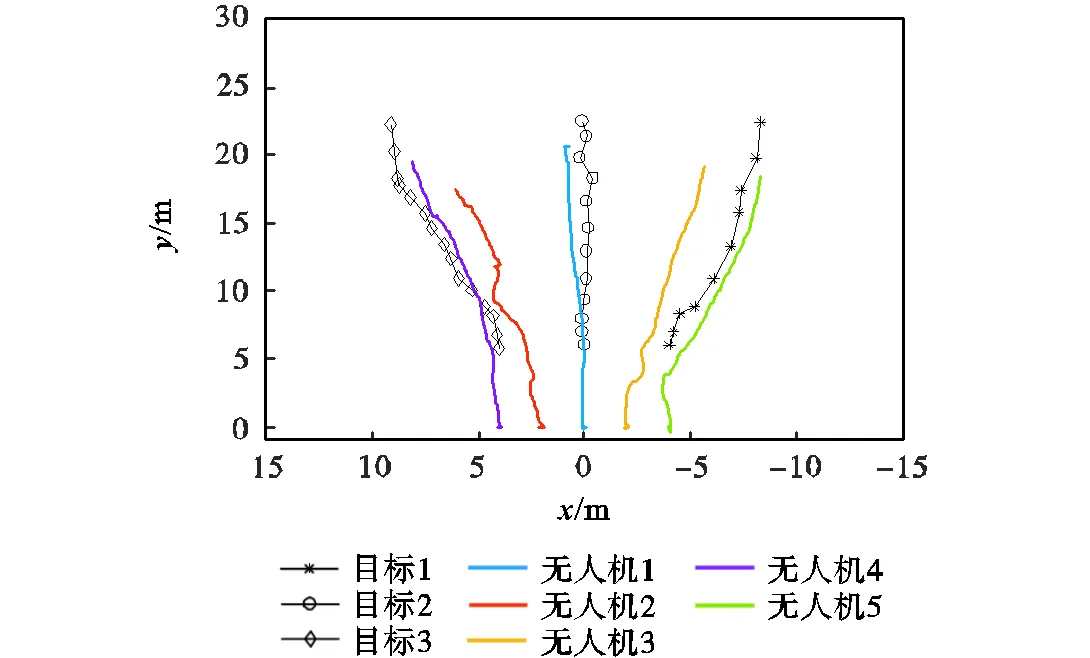
图14 二维无人机与地面目标运动轨迹

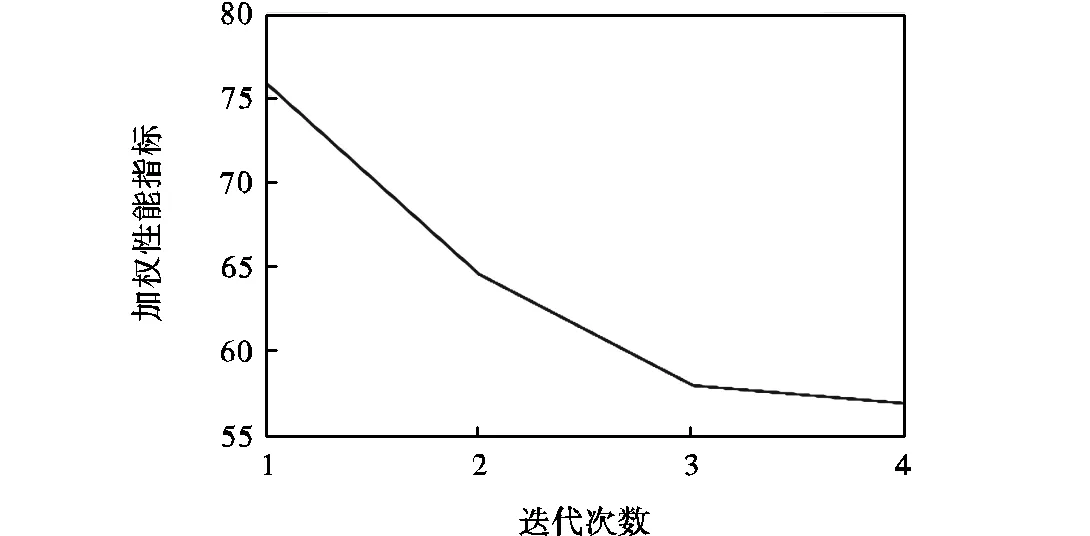
图15 户外实验中拍卖鸽群优化算法优化曲线

4 结 语

本文对多无人机协同追踪场景的分布式任务分配进行了建模和算法设计．建立了包含3个性能指标和两个约束条件的分布式任务分配模型．在此基础上，提出了拍卖鸽群优化算法，将拍卖策略作为分布式实现框架，并设计了一种基于目标优先级的任务分配方案解算策略，引入鸽群优化算法更新各无人机的竞拍价，最后通过数值仿真、Gazebo虚拟仿真、实机户外实验证明了算法的有效性和实用性．目前的研究仅实现了在相对理想条件下的追踪场景任务分配，仍有许多方面需要继续深入研究和改进，例如：多无人机任务分配和航迹规划一体化的研究；满足更多约束的任务分配算法研究．

［1］ 侯永宏，刘 艳，吕华龙，等. 一种基于双目视觉的无人机自主导航系统[J]. 天津大学学报(自然科学与工程技术版)，2019，52(12)：1262-1269.

Hou Yonghong，Liu Yan，Lü Hualong，et al. An autonomous navigation systems of UAVs based on bin-ocular vision[J]. Journal of Tianjin University (Science and Technology)，2019，52(12)：1262-1269(in Chi-nese).

［2］ Kurdi H A，Ebtesam A，Maram A，et al. Autonomous task allocation for multi-UAV systems based on the lo-cust elastic behavior[J]. Applied Soft Computing，2018，71(1)：110-126.

［3］ Silvestrin P V，Ritt M. An iterated tabu search for the multi-compartment vehicle routing problem[J]. Com-puters & Operations Research，2017，81(1)：192-202.

［4］ 李 俨，董玉娜. 基于SA-DPSO混合优化算法的协同空战火力分配[J]. 航空学报，2010，31(3)：626-631.

Li Yan，Dong Yuna. Weapon-target assignment based on simulated annealing and discrete particle swarm optimi-zation in cooperative air combat[J]. Acta Aeronautica et Astronautica Sinica，2010，31(3)：626-631 (in Chinese).

［5］ Muhuri P K，Rauniyar A. Immigrants based adaptive genetic algorithms for task allocation in multi-robot sys-tems[J]. International Journal of Computational In-telligence and Applications，2017，16(1)：1750025.

［6］ Pendharkar P C. An ant colony optimization heuristic for constrained task allocation problem[J]. Journal of Com-putational Science，2015，7(1)：37-47.

［7］ Cui R X，Guo J，Gao B. Game theory-based negotia-tion for multiple robots task allocation[J]. Robotica，2013，31(6)：923-934.

［8］ Bonabeau E，Sobkowski A，Guy T，et al. Adaptive task allocation inspired by a model of division of labor in social insects[C]// Biocomputation and Emergent Com-puting，1997：36-45.

［9］ Bertsekas D P. The auction algorithm：A distributed relaxation method for the assignment problem[J]. Annals of Operations Research，1988，14(1)：105-123.

［10］ Adhau S，Mittal M L，Mittal A. A multi-agent system for distributed multi-project scheduling：An auction-based negotiation approach[J]. Engineering Applications of Artificial Intelligence，2012，25(8)：1738-1751.

［11］ Edalat N，Tham C K，Xiao W. An auction-based strat-egy for distributed task allocation in wireless sensor net-works[J]. Computer Communications，2012，35(8)：916-928.

［12］ Song T，Yan X，Liang A，et al. A distributed bidirec-tional auction algorithm for multi-robot coordination[C]// 2009 International Conference on Research Challenges in Computer Science. Shanghai，China，2009：145-148.

［13］ Saravanan S，Ramanathan K C，Ramya M M，et al. Review on state-of-the-art dynamic task allocation strate-gies for multiple-robot systems[J]. Industrial Robot，2020，14(1)：929-942.

［14］ Lee D H，Zaheer S A，Kim J H. A resource-oriented，decentralized auction algorithm for multirobot task allo-cation[J]. IEEE Transactions on Automation Science & Engineering，2015，47(6)：1469-1481.

［15］ Braquet M，Bakolas E. Greedy decentralized auction-based task allocation for multi-agent systems[J]. IFAC-Papers on Line，2021，54(20)：675-680.

［16］ Qiu H，Duan H. Multi-objective pigeon-inspired optimi-zation for brushless direct current motor parameter de-sign[J]. Science China Technological Sciences，2015，58(11)：1915-1923.

［17］ Li C，Duan H. Target detection approach for UAVs via improved pigeon-inspired optimization and edge poten-tial function[J]. Aerospace Science and Technology，2014，39(1)：352-360.

［18］ Duan H，Wang X. Echo state networks with orthogonal pigeon-inspired optimization for image restoration[J]. IEEE Transactions on Neural Networks and Learning Systems，2016，27(11)：2413-2425.

［19］ Hu C，Qu G，Zhang Y. Pigeon-inspired fuzzy multi-objective task allocation of unmanned aerial vehicles for multi-target tracking[J]. Applied Soft Computing，2022，126(1)：109310.

［20］ Duan H，Qiao P，Yang Y. Pigeon-inspired optimiza-tion：A new swarm intelligence optimizer for air robot path planning[J]. International Journal of Intelligent Comput-ing & Cybernetics，2014，7(1)：24-37.

Distributed Task Allocation Based on Auction-PIO Algorithm for Multi-UAV Tracking

Hu Chaofang，Song Sihan，Xu Jiajun，Wang Didi

(School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China)

Unmanned aerial vehicle(UAV)technology has been applied widely in various research fields. Task allocation is crucial in multi-UAV cooperation and has a significant impact on the quality of task completion. In this paper，a distributed allocation method based on auction algorithm with pigeon-inspired optimization(auction-PIO)was proposed for multi-UAV task allocation in a multi-target tracking scenario. First，three performance indices including total tracking distance，allocation balance，and task completion time，were proposed. Along with the constraints of the tracking task，a distributed multi-index 0-1 integer programming model was established. Second，the auction strategy was used as the distributed optimization framework，and the UAV was regarded as the auctioneer to bid for the ground target. The task allocation result was determined through multiple rounds of bidding. In order to enhance the optimality of allocation，the information shared among UAVs was increased such that UAVs were able to bid for all targets. Additionally，the PIOalgorithm was introduced to update the bidding prices for targets. The position of pigeon was encoded into the increment of UAVs bidding prices for targets. The map compass operator and landmark operator were used to update swarm positions iteratively so that the bidding prices of UAVs could be updated as well. On this basis，a solution strategy based on target priority was designed to convert the computation result of bidding matrix and distance matrix into allocation matching relationship. Moreover，the computational complexity of the proposed algorithm was analyzed. Finally，the numerical simulation，Gazebo virtual simulation，and outdoor flight experiment of actual UAVs were implemented for the proposed algorithm. The results show that the proposed auction-PIO algorithm has a good allocation performance. In the numerical simulation，the optimization performance of the proposed algorithm is improved by 12.16% compared with that of the classical auction algorithm. Moreover，the virtual simulation and the outdoor experiment also show that the proposed algorithm can meet the requirement of practicability.

unmanned aerial vehicle(UAV)；target tracking；task allocation；auction；pigeon-inspired optimization(PIO)

V279

A

0493-2137(2024)04-0403-12

10.11784/tdxbz202301009

2023-01-09；

2023-03-13.

胡超芳（1973—  ），男，博士，教授.

胡超芳，cfhu@tju.edu.cn.

天津市科技计划资助项目(19YFHBQY00040)；天津大学自主创新基金资助项目(2022XSU-0003).

the Science and Technology Program of Tianjin，China(No.19YFHBQY00040)，Tianjin University Innovation Foundation (No.2022XSU-0003).

(责任编辑：孙立华)