中国工业碳排放网络结构演化特征与链路预测
彭邦文,郑闳方,朱 磊,胡文倩(.湖南工商大学经济与贸易学院,湖南 长沙 4005;.深圳大学电子与信息工程学院,广东 深圳 58060;.西安建筑科技大学公共管理学院,陕西 西安 70055)
据测算,中国碳排放超过63.06%来源于工业部门[1],因此控制工业部门碳排放是实现中国经济低碳发展的重点任务.同时,我国双碳”目标的提出,也为如何科学实现工业部门碳减排提出了新命题.在中国面对巨大碳减排压力下,按照不同行业碳排放量差异划分不同减排责任,一直被认为是有效实施碳减排的主要方式之一.但如果行业间割裂地实施自身行业碳减排策略,不仅不会提升碳减排效率,反而会增加碳减排难度和成本,造成严重资源浪费和市场混乱,而且对碳减排政策制定存在一定误导性,无法从根本上进行有效碳减排[2-3].因此,揭示中国工业子行业之间碳排放的复杂关联结构形态,探寻不同行业在碳排放关联结构中扮演的角色和所处地位,对于建立健全跨行业协同碳减排机制具有重要意义.
采用复杂网络范式研究产业部门之间碳关联性,已经取得较多进展.在研究主题上,不同学者从全产业碳足迹网络[4-5]、国际贸易碳排放转移网络[6-9]、制造业碳排放网络[10]、高耗能碳关联网络[11]、建筑业碳排放网络[12]等不同视角出发对网络整体特征、个体特征、行业聚类特征以及影响因素等进行了分析,但针对于中国工业碳排放网络的研究相对较少.在研究方法上,通常需要两个连续的方法来揭示行业间碳排放关联结构,一是碳排放网络构建方法,二是针对所构建网络进行结构及其影响因素等分析的方法.而关于后者,对网络整体结构特征进行分析的网络密度、聚集系数、平均最短路径长度等方法[8,13],对个体网络特征进行分析的点度中心度、中介中心度、接近中心度等方法[5,13-14],对网络进行聚类和碳关联路径分析的块模型等方法[4,14-15],对网络影响因素进行分析的二次指派程序(QAP)或者指数随机图模型(ERGM)[8]等研究方法,都已经较为成熟.而在网络构建方法中,最为关键的环节是如何识别网络节点间强关联关系,不同学者的方法却各不相同,例如常见两种网络构建方法上,诸多学者采用完全消耗系数或者碳流量等矩阵数据总额的固定百分比值(例如算术平均值)作为阈值来识别网络链路[4,13,16],也有学者采用威弗-托马斯指数(WI)作为列阈值来识别网络链路[17-18].这些方法虽然在截面数据的运用中也能较好展现出行业间碳排放结构化信息或者网络关联系统的“骨架”,但没有体现工业系统中产品生产的直接消耗和间接消耗过程的信息,并且因为没有考虑经济系统演进过程中的技术性变化,可能会导致此类方法的阈值设置具有一定随意性,因此难以运用在多年份的演化网络构建中.在数据利用上,采用投入产出数据作为产业关联碳足迹研究的基础数据已经作为当前行业间碳排放关联网络研究中的主流应用.例如,部分学者采用中国不同年份的投入产出表数据,从不同角度对中国产业间碳排放网络进行了研究[4-5,13,19].也有学者以Eora 数据库、世界投入产出数据库(WIOD)中的世界投入产出表数据为基础,探讨了全球贸易隐含碳流动网络的特征[7-8].但这些研究对投入产出表数据采用的年份与论文发表年份都相差较远.这是因为编制一个国家或地区的投入产出表,通常需要投入大量人力、物力和财力,这使得单个国家不得不5a 左右才编制一次投入产出基准表[7],并且投入产出基准表数据收集整理至发布至少需要2~3a 时间,2022 年的中国投入产出表预计在2025 年左右公布[20],这也造成相关行业间碳排放网络研究的时效性不足,因而在网络框架下对行业间碳排放未来链路进行科学预测就成为一个新颖而又兼具现实意义的话题.
鉴于此,本文将经济投入产出生命周期评价(EIO-LCA)与最小流分析(MFA)方法结合构建了中国工业碳排放网络,结合社会网络分析方法(SNA)对中国工业碳排放网络结构特征进行了分析,并预测了2022 年的中国工业碳排放网络.
1 方法与数据
1.1 工业碳排放网络构建方法
采用经济投入产出生命周期评价(EIO-LCA)方法得到中国工业各行业间的碳关联矩阵.EIO-LCA方法包括经济投入产出表和环境影响系数两部分,即将“环境”部门追加在投入产出表的列向量中,其他相关行业污染物的“产出”都用此列向量的行值表示[21].与传统的环境投入产出法类似,污染物排放系数转变为对角矩阵,以便于将最终需求引起的环境影响分解到生产链的各个行业.但这种方法计算出来的结果只能得出每个行业的碳排放量,无法识别行业间的碳排放关联.借鉴Li 等[22]的处理方式,对EIO-LCA 模型进行调整,将最终需求的列向量形式转化成对角矩阵,这样就可以得出行业间碳排放的“关系数据”,而不是“属性数据”.
式中:B 为各行业间的碳排放矩阵;bij为B 中元素,表示i 行业在产品生产或提供服务过程中因使用行业j 的产品或服务而产生的碳隐含排放量; i(j)=1,…,n,其中n 为投入产出中的行业数;为对角矩阵,表示各个行业的直接能源消费碳排放强度[23],对角元素为Ri=cei/xi,cei为行业i的直接碳排放量,xi为行业i 的增加值.(I-A)-1为里昂惕夫逆矩阵,反映了经济体的中间投入产出结构以及生产技术水平,其中I为单位矩阵,A 为国内投入部分的直接消耗系数矩阵,aij为A 的元素,表示第j 个行业增加一个单位的最终需求时所需要的i 行业的产出;为对角矩阵,剔除进口部分的最终需求量,对角元素yi表示j 行业产品或服务的最终需求量(包括居民最终消费量、政府最终需求量、资本形成与出口量).根据得到行业间碳排放关联矩阵,可以得到包含权重和方向的行业间碳排放关联关系,该矩阵能准确反映行业间碳排放关联的程度与作用路径.但行业间碳排放关联的量级是不同的,很多行业碳排放关联程度不强,这就使得如何识别出行业碳排放关联系统中主要的关联关系(或强关联关系)成为必要.本文基于Schnabl 提出的最小流分析(MFA)方法识别阈值[24],该方法被认为能更好识别出行业间强关联关系[25].具体步骤如 下:
1.1.1 根据碳排放关联矩阵划分区间 根据碳排放关联矩阵,寻找最大过滤值 fmax,使得当以任何小于等于 fmax的值为阈值时,系统存在双向关联,而以任何大于 fmax的值为阈值时,系统以前存在双向关联而现在不存在双向关联.将区间[0, fmax]按等间距分为l 份,共得到 l+1个端点,将这些端点设为阈值 fl,随着阈值 fl的增大,双向关联逐渐成为单向关联、弱关联甚至不关联.
1.1.2 计算关联矩阵M 对于每一阈值fl,计算对应的关联矩阵M,先将碳排放关联矩阵B 进行欧拉序列分解:
式中:A1为直接消耗系数矩阵;A2…Ak分别是不同层级的间接消耗系数矩阵,分别计算不同层级的流量矩阵,也即
然后将各层流量矩阵Tk根据表1 原则转换为Wk:

表1 连接矩阵转化原则Table 1 Principles of connection matrix transformation

表2 中国工业碳排放关联网络的整体特征指数Table 2 Overall characteristic index of China's industrial carbon emission correlation network
由于系数矩阵A 服从衰减过程,当阈值fl>0 时,k很少超过6 步,本文在这里取k=6.接着计算第k 步关联矩阵Wk,公式如下:
式中:“#”代表布尔运算规则,Wk中的k 指的是k 步距离的关联,而不是幂次.最后计算关联矩阵M,公式如下:
1.1.3 计算连通性矩阵H 对于每一阈值fl对应的关联矩阵M,计算连通性矩阵H.首先利用布尔运算规则,计算弱连通矩阵E.
1.1.4 确定最终阈值f*根据连通性矩阵H,确定最终阈值f*,得到最终关联矩阵L.最终阈值为以下3个阈值中最接近它们平均值的阈值:
(1)根据熵最大原则,确定f1.计算每一阈值fl对应的H 矩阵的熵Gl:
式中:m 为hij的取值范围;plm为hij每一取值所对应的概率.比较每一个fl对应的Gl,确定最大熵值Gmax,Gmax对应着H 中所有元素(为0,1,2,3)出现概率相互最接近(或相等)时的情况.将最大熵值Gmax所对应的阈值设定为f1.
(2)由于每一个fl对应一个Hl,对所有H 矩阵中的元素进行加和平均后得到 Have, 其中have,ij=(h1,ij+h2,ij+ …+hl+1,ij)/(l +1).将得到的Have结构与各fl对应的Hl矩阵比较,找到与Have结构最相似的矩阵H′.考虑关联结构的相似性,分别计算每一个Hl与Have中对应元素的离差平方和Ql:
比较每一个fl对应的Ql,确定最小的离差平方和Fmin,将Fmin所对应的阈值设定为f2.
(3)对于存在双向(hij= 3)和单向(hij= 2)关联的行业i、j,其eij一定为1,所以当行业网络为连通图时,eij=1 是冗余信息,可从H 矩阵中减去,得到连通性矩阵Hres,Hres是关联矩阵M 和其转置矩阵之和.其中 hres,ij= 2对应于双向关联, hres,ij= 1对应于单向关联.由于研究过程关注重点为行业间的双向关联及单向关联,故以 Hres矩阵中 hres,ij= 2的个数与hres,ij= 1的个数最接近为原则,寻找联通矩阵H′,H′所对应的阈值为f3.
1.1.5 计算f1,f2,f3的平均值与平均值最接近的阈值设为最终阈值f*.根据最终阈值f*,将少于阈值的弱关联关系赋值为0,大于或者等于阈值的关联关系有两种处理方式,一种保留每条弧的权重,另外一种是对存在强关联关系的弧赋值为1.上述两种处理方式分别得到有向加权与有向无权两种网络.
1.2 基于SNA 方法的网络结构特征测度方法
本文采用网络密度、网络关联度、网络等级度与网络效率4 个指标来反映网络的整体特征[26-27].采用点度中心度(包含入度与出度值)、中介中心度与接近中心度3 个指标来衡量个体网络特征[26-28].并采用块模型分析方法对整个网络的聚类信息进行挖掘[29-30].相关指标的具体计算公式以及块模型的划分依据与应用请参照对应文献.
1.3 基于链路动态变化的碳排放关联网络预测方法
王斌等[31]基于无向加权行业网络构建了链路动态变化的行业网络预测模型,该模型既考虑了两个节点之间的相似性程度受共同邻居节点的影响,又考虑了在前期网络和当前网络中链路权重的变化程度,并且证明了比目前应用最为广泛的相似性链路预测算法有更好精度.与之不同的是,本文的算法建立在有向加权网络的基础上,使得不仅可以掌握每个行业未来的度数中心性特征,也可以获悉每个行业碳流入与碳流出等变化信息.此外,因行业之间的技术关联存在一定粘性[35],本文在算法上放宽了节点之间受共同邻居节点影响的假设.基于链路动态变化的碳排放关联网络预测模型算法如下:
设(u , v )为行业节点u 指向行业节点v 的弧, ω( u , v)表示该条弧的权重.因为弧的权重都是随时间 t ∈ [0, +∞ )的变化而变化,因此权重 ω( u , v , t)可以表示为时间t 的函数.在网络中,弧的权重随时间的增减数值各异,为便于定义随后的预测得分,引进变化率 r(0< r< 1).当弧的权重 ω( u , v , t)从t1到t 显著增加时,其属于集合 E1=[0,(1 −r )ω(u , v, t1));当弧的权重 ω( u , v , t)从t1到t 变化不大时,其属于集合E2= [(1 −r )ω(u , v, t1),(1 +r )ω(u , v, t1));当弧的权重ω( u , v , t)从 t1到 t 显著减少时,其属于集合E2= [(1 +r )ω(u , v, t1), +∞) .显然 E1∩ E2∩ E3= φ,而且 E1∩ E2∩ E3=Ω.
当网络从t1时刻的状态演化到t 时刻的状态时,若弧的权重 ω( u , v , t)较权重ω(u , v, t1)减少,且ω( u , v, t )∈ E1时,定义此时的衰减函数为:
式中:δ为负数,表示权重在衰减.
当网络从t1时刻的状态演化到t 时刻的状态时,若弧的权重 ω( u , v , t)较权重ω(u , v, t1)变化不大,且ω(u , v, t )∈ E2时,定义此时的不变函数为:
式中:η为非负数,表示权重的变化不大,可以忽略不计.
当网络从t1时刻的状态演化到t 时刻的状态时,若弧的权重 ω( u , v , t)较权重ω(u , v, t1)增加,且ω( u , v, t )∈ E3时,定义此时的增加函数为:
式中:θ为非负数,表示权重在增加.而根据上述定义,参数δ、η、θ之间的关系为θ > η > δ.同时参数r,δ,η,θ取值根据预测精度值最大时来确定.此外在ω(u , v, t1) = 0的情形下, 若 ω( u , v, t ) = 0, 则令P(u , v , t ) = 0;若 ω( u , v, t) ≠ 0,则令 P(u , v, t )= θ.
定义弧(u , v )在区间 [ t1, t2], t2> t1上的预测得分score( u , v )为:
式中: IEi( i=1,2,3)是Ei的示性函数.score(u,v)衡量了网络中弧( u,v)从t1时刻的状态演化到t2时刻的状态时的得分,这样就将投入产出表5a 更新一次导致数据的离散跳跃转化成了连续性变化模型.利用该得分函数,就可以预测两两节点之间弧的得分值或者节点之间的有向加权得分矩阵,通过给该矩阵确立合适的阈值,排除掉弱关联关系,就可以得到有向加权的预测网络.
1.4 数据来源
中国投入产出基准表每5a 编制一次,因各年份投入产出表行业分类标准不一,出于产业归并时保留更多行业细分信息的考虑,这里选择1997 年为起始年份,又因为最新年份中国投入产出基准表只到2017 年,所以选取1997、2002、2007、2012、2017年的中国投入产出基准表作为基础数据.5 个年份的投入产出表均来自中国国家统计局国民经济核算司,其中1997、2002、2007、2012、2017 年的行业部门数分别为124、122、135、139、149.此外,参考IPCC(2006)公布的碳排放计算方法和参数并结合中国官方公布的相关参数对每个行业i 的直接碳排放量cei进行估算,公式如下[32]:
式中:j 表示能源种类,为保证估算结果的准确性,全面考虑了统计年鉴中连续报告的16 种化石能源,包括原煤、洗精煤、其他洗煤、焦炭、其他焦化产品、焦炉燃气、其他燃气、原油、汽油、煤油、柴油、燃料油、其他石油制品、液化石油气、炼厂干气、天然气;cei为i行业的能源消费碳排放总量,百万t;Fij为i 行业j 种能源的终端化石能源消费量,百万t 或百亿m3,不包括用于产品制造原料的消费量),数据来自对应年份的《中国能源统计年鉴》;CVj为第j种能源平均低位发热值,kJ/kg 或kJ/m3,来自《中国能源统计年鉴》(2014);CCFj为第j 种能源燃料的碳含量(kg/106kJ),来自《2006 年IPCC 国家温室气体清单指南》;COFj为第j 种能源碳氧化率,来自《中国省级温室气体清单编制指南》;44 和12 分别表示CO2分子量和C 原子量.此外,为了使得投入产出表与《中国能源统计年鉴》中行业分类相对应,基于数据可比性原则和细分产业数量保留最大化两个原则,参考中国国民经济行业分类标准(GB/T 4754-2011),按照其中的大类、中类和小类划分的相互隶属关系,将所要分析的各年份工业调整为30 个子行业(行业代码与行业名称见表3).其中将各年份投入产出表中的文教玩具体育用品制造、机械设备修理、工艺美术品制造、废品废料、废弃资源和废旧材料回收加工品、机械设备修理服务等难以形成连续数据的行业归并为“其他制造业”.
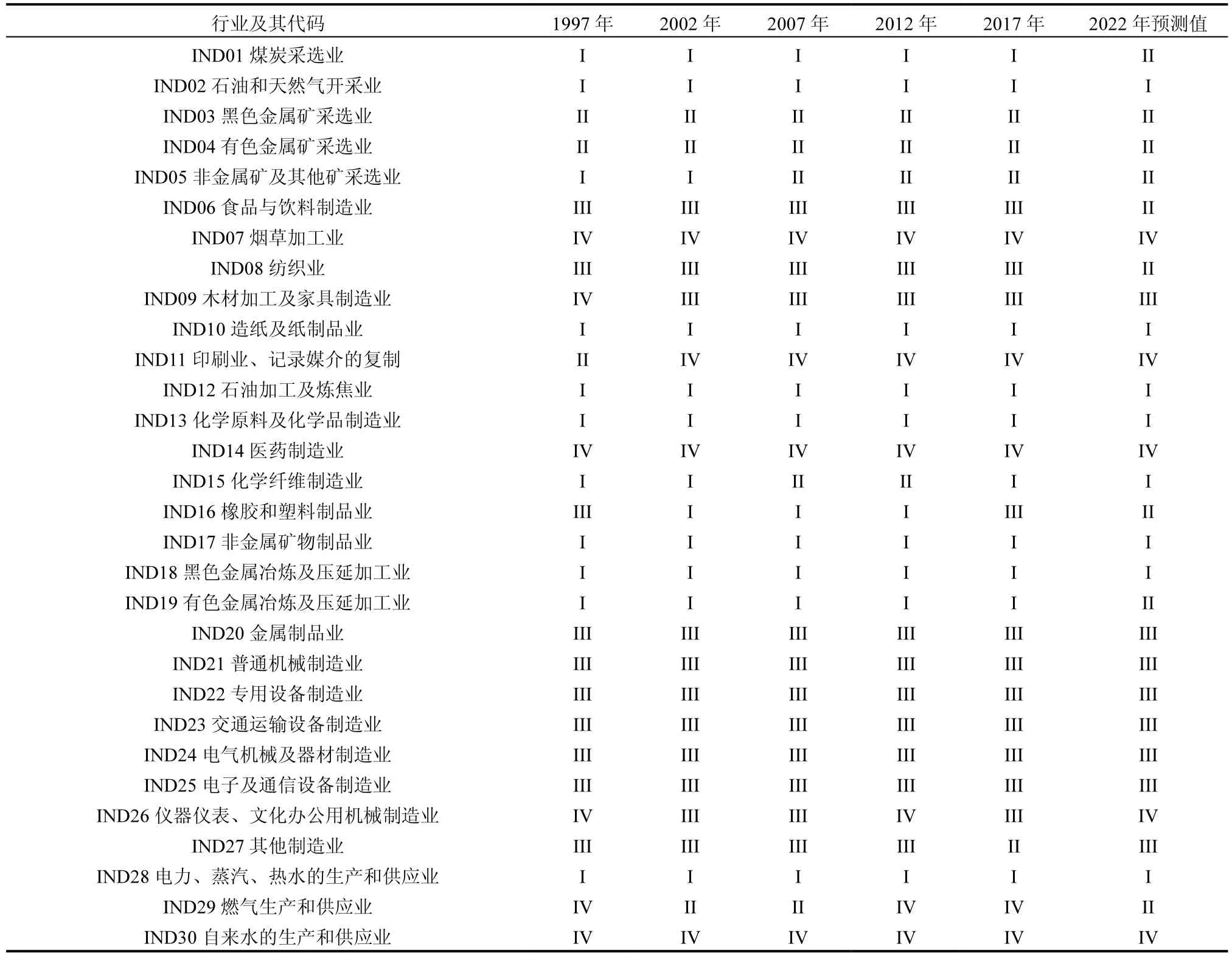
表3 中国工业碳排放网络的各板块组成成员与变动Table 3 Composition and changes of various sections of China's industrial carbon emission network
2 中国工业碳排放关联网络的演化特征
2.1 整体网络特征的演变趋势
本文结合所构建的碳排放关联网络构建方法,以MFA 方法确定工业碳排放关联矩阵的阈值后,在有向无权网络的基础上,1997、2007 与2017 年30 个行业的中国工业碳排放关联拓扑网络如图1 所示.

图1 中国工业碳排放关联拓扑网络Fig.1 Topological network of China's industrial carbon emissions association
网络密度从1997 年的0.261 上升到了2017 年的0.356,基本上呈现递增的趋势,说明中国工业碳排放网络的子行业之间碳关联关系越来越紧密.网络等级度从1997 年的0.552 下降到了2017 年的0.301,基本呈现递减趋势.网络效率在样本期内呈现波动下降趋势,这意味着中国工业碳排放网络中的连线在增加,网络的稳定性在逐步提升.网络关联度除1997 年因为有一个行业被排除在主体网络之外,导致该年度关联度为0.933 之外,其他年份网络关联度都为1,这表明中国工业碳排放关联网络连通性较好,工业各行业之间具有普遍碳排放关联效应.上述4个衡量网络整体性的指标测算结果,都表征着中国工业碳排放网络的复杂性和节点地位均衡性在增强.究其原因,中国工业碳排放网络的这种结构性变化,很大程度是由我国工业体系的完整性越来越高引致的.在比较优势和国际自由贸易环境相互作用下,工业体系不完整性容易导致少数行业在整个工业网络中占有重要地位.而随着工业体系完整性和产业发展均衡性增强,少数行业在碳关联网络中占有核心地位的结构被逐渐打破,更多的行业逐渐往网络核心地位靠拢,这也意味着很难通过孤立的单个行业节能减排政策来实现工业整体碳排放减少这一目的.
2.2 个体网络特征及演变趋势
2.2.1 点度中心度 由图2(a)、(b)可见,从不同行业部门的入度值来看,主要承担机械与设备制造职能的5 个重工业部门(IND21~IND25)处于发挥碳吸入作用的“第一方阵”,这些部门的碳排放入度值较高是因为这些部门生产的产品技术复杂度较高,需要众多其他部门提供中间产品;而金属制品业(IND20)、食品与饮料制造业(IND06)、木材加工及家具制造业(IND09)、纺织业(IND08)3 个行业部门则处于碳吸入效应的相对高位.从不同行业的出度值来看,黑色金属冶炼及压延加工业(IND18)、化学原料及化学品制造业(IND13)与石油加工及炼焦业(IND12)排在前3 位,而采选业中的煤炭采选业(IND01)与石油和天然气开采业(IND02)、造纸及纸制品业(IND10)、非金属矿物制品业(IND17)、有色金属冶炼及压延加工业(IND19)、电力、蒸汽、热水的生产和供应业(IND28)在中国工业碳排放关联网络中主要发挥了较强的碳溢出作用.中国工业碳排放网络之所以出现这种点度中心度分布特点,主要是由不同行业在产业链中的位置决定的.入度值较高的重工业部门多处于整个工业体系的相对下游,需要众多其他行业为其提供中间产品,因此成为了主要的碳关联关系的吸入部门.而出度值较高的基础性行业部门多处于整个工业体系的相对上游,多是对原材料进行生产和初步加工的行业,所生产的中间产品多是为下游的行业部门所使用,所以在上游行业输送中间产品至下游行业的同时,也带来了大量的碳关联关系溢出.而从演化视角来看,5 个重工业部门(IND20~IND25)在1997~2017 年之间碳吸入关系数的增长速度最快,非金属矿及其他矿采选业(IND05)以及食品与饮料制造业(IND06)的碳溢出关系数的增长速度相对较快,这些行业应成为未来碳减排重点监测的对象.
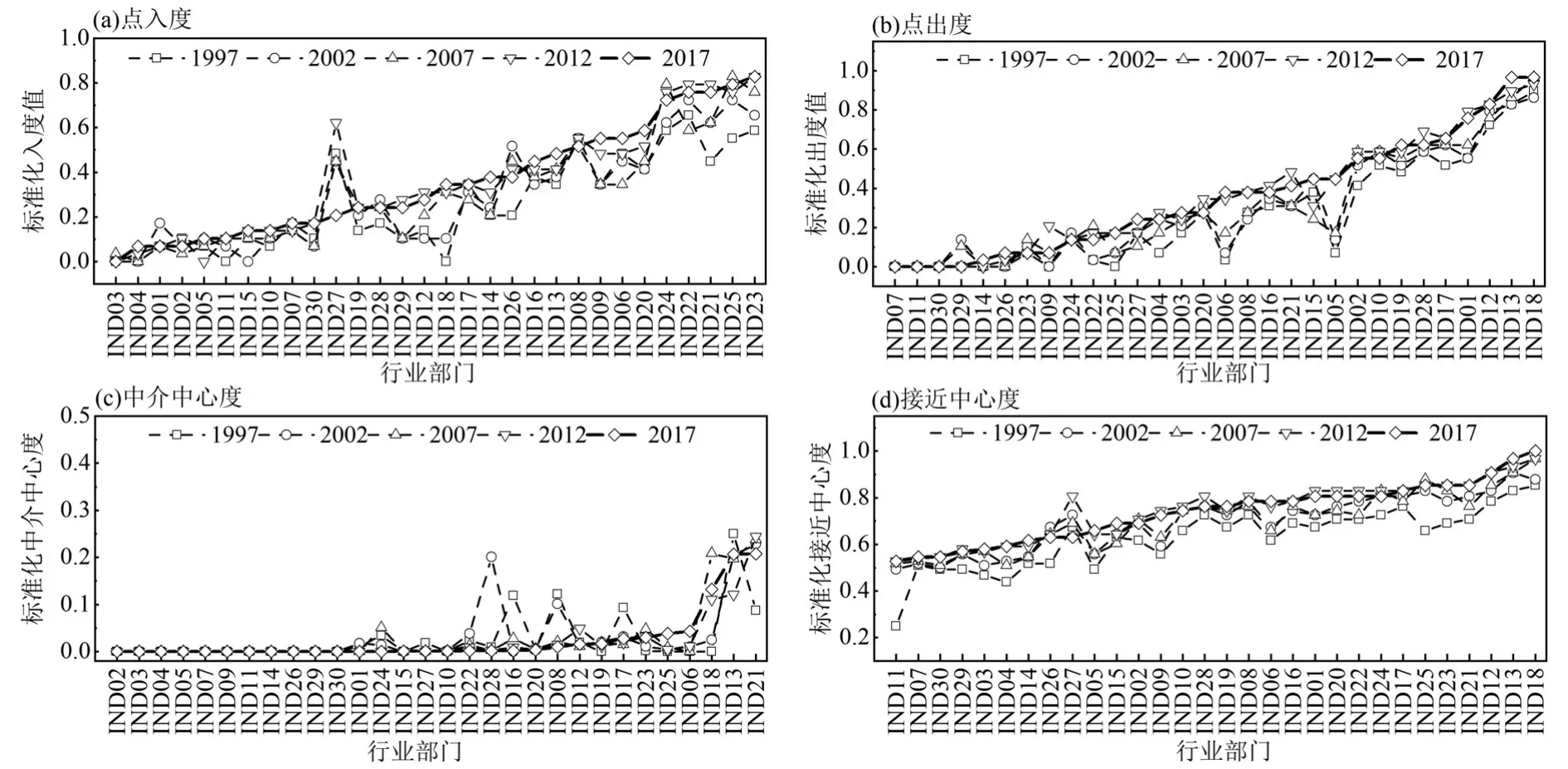
图2 中国工业碳排放关联网络的各类中心度演化趋势Fig.2 Evolution trend of various centrality of China's industrial carbon emission correlation network
从图3 可见,不存在既有着较高入度值同时又有着较高出度值的行业部门,也即不存在同时具有显著碳吸入效应与碳溢出效应的行业部门.具有“高入度—低出度”的行业部门的数量占比20%,具有“低入度—高出度”的行业部门的数量占比30%,有50%的行业部门属于“低入度—低出度”特征部门,这也为分类治理提供了便利.针对具有“低入度—高出度”特征的行业部门,这些行业部门处于整个工业产业链相对上游,行业部门的能源强度较高,因此要在生产过程中通过增加清洁能源的使用来降低化石能源使用比例,提升绿色创新水平等手段,努力降低单位产出的能耗.而“高入度—低出度”的行业部门更多处于工业产业链的下游,这些行业部门的一次能源使用量使用较少,要通过提高资源循环利用水平和形成产业集聚等方式,降低单位产出的物耗.

图3 中国工业碳排放关联网络的点度中心度散点Fig.3 Scatter plot of degree centrality of China's industrial carbon emission correlation network
2.2.2 中介中心度 图2(c)显现出两个显著特点.其一,某些行业出现了无规则的变化趋势,例如电力、蒸汽、热水的生产和供应业(IND28)在2002 年的中介中心度达到了0.201,但其他年份都显著少于0.100,这可能是特定年份的经济结构变动导致的,具有一定的偶然性,这也间接说明采用长年份分析的必要性.其二,普通机械制造业(IND21)、化学原料及化学品制造业(IND13)与黑色金属冶炼及压延加工业(IND18)3 个行业部门在研究期内基本处于前3 位,这也表明这些部门在中国整个工业碳排放关联网络中展现出较强的“桥梁”作用,在产业协同减排的过程中,有效合理控制这些部门的碳排放,可以有效阻断这些行业部门与其他部门之间的碳关联,从而达到整体减排的效果.从图2(c)中也可以看出,除3个行业相较于前述不同年份有不同程度的下降之外,其他行业中介中心度在2012~2017 年之间的变动幅度较小,这一定程度表明了3 个行业在碳排放网络中的“桥梁”作用在减弱,也表明其他行业之间的碳关联关系在不断增强,这也与整体网络特征的表征具有一致性.
2.2.3 接近中心度 图2(d)可见,在1997~2017 年间,绝大多数行业的接近中心性呈现波动上升趋势,这说明整个中国工业碳排放关联网络的碳流动效率越来越高.而从行业部门的个体特征来看,黑色金属冶炼及压延加工业(IND18)、化学原料及化学品制造业(IND13)与石油加工及炼焦业(IND12)3 个行业部门的接近中心度在2017 年都达到了0.9 以上,处于第一梯队.此外,值得关注的是,机械与设备制造的5个重工业部门(IND21~IND25)的接近中心性在2012 与2017 年都介于0.8~0.9 之间,处于第二梯队.上述这些行业部门能在碳排放关联网络中能更便捷地与其他行业部门相关联,在网络中扮演“中心行动者”角色,也说明这些行业部门能在网络中具有较强低碳技术和资源获取能力,能通过较高的链接效率,带动其他处于边缘位置的行业部门进行协同减排.
2.3 块模型分析
针对图1 显示的网络,对31 个行业的碳关联关系进行块模型分析.采用CONCOR方法,选择最大分割深度为2,收敛标准为0.2,最大迭代次数2500 次,将30 个行业划分为4 个板块,就得到各个板块内部与板块间关联数组成的密度矩阵,将各年份碳关联网络的整体密度视为判定标准,将大于整体密度的关联关系视为显著关联.各个板块的行业成员构成及其演变见表3.样本期内各个板块之间的关联关系及其演变如图4 所示,图中箭头所示数字为板块间碳关联关系的显著程度,其值介于0~1 之间,越趋近于1,代表碳溢出(碳吸入)效应越大.R2表示块模型的拟合优度.
从板块关联属性及其成员构成来看,板块I 主要包括了能源开采行业(IND01-02)与基础工业产品制造行业(IND10、12、13、15~19、28),板块I 总体上作为双向溢出板块,不仅对自身板块内部有着较多碳溢出,也对板块III 与板块IV 有着碳溢出,其中对于板块III 的碳溢出关系尤为显著,在1997~2017年之间,碳关联密度长期保持在0.890 以上.因此板块I 作为中国整个碳关联网络的源头板块,在完善碳减排政策时应当给予优先考虑.板块II 主要包括了金属矿采选业(IND03~04)与非金属矿采选业(IND05),除去1997 年板块II 作为孤立板块之外,后续年份板块II 均扮演着重要的溢出板块角色,其内部的产业碳关联较少,主要对板块III 产生碳溢出.板块III 的成员主要是机械制造业(IND21~27)与部分轻工业(IND06、08、09),板块III 作为双向受溢板块,不仅板块内部行业部门之间存在着显著的碳关联,也接受板块I 和板块II 的碳溢出.板块IV 的成员主要包括燃气生产和供应业、自来水的生产和供应业以及部分轻工业(IND07、11、14),板块IV 作为受溢板块,主要接受来自板块I 的碳溢出.上述块模型的结果可在一定程度上视为网络个体特征的延续,但与其不同的是,块模型更好地展示了不同板块之间的碳流入流出关系以及板块自身碳关联程度.而针对不同板块及其关联的特征,应该实施分类治理的措施,来实现我国工业子行业部门整体减排的目标.例如,对于具有“溢出”属性的板块I 与板块II,要注重发挥绿色技术创新与新能源利用的作用,带动其直接碳排放强度的下降,减弱其对其他行业碳排放的带动作用.对于具有“受溢”属性的板块III 与板块IV,可以通过减少中间品使用,或者通过制定更严苛的中间品采购环境标准等的方式倒逼上游行业进行技术变革,来降低因“受溢”而引致的碳排放程度.而对于板块内部有着显著自我关联属性的板块I 与板块III,由于板块内部各个子行业之间的碳关联关系错综复杂,并且板块成员的技术关联紧密,应对其制定组团式减排政策,充分利用搭建绿色技术共享平台、提供专项减排激励措施等手段进行重点治理.
从板块间关联关系演化角度来分析,1997~2007年间板块关系存在着一定变动,1997 年板块II 与所有板块之间均不存在显著关联性,但从2002 年开始变成净溢出板块,而板块IV 除了在2002 年与所有板块之间均不存在显著关联性之外,其它年份都为净受溢板块.板块II 与板块IV 的内部行业之间并没有存在显著的关联关系.板块I 与板块III 的内部行业部门之间存在较大的关联密度,并且在1997~2012年间存在着较大增幅,而在2017 年出现了小幅度下降趋势.而且从2002 年开始,板块III 接受来自板块I与板块II 的显著碳溢出,并在2012 年接受板块I 的碳溢出达到了1.000,这表明板块I 中所有行业部门都对板块III 的行业部门产生了碳溢出.2007~2017年之间板块间关联关系变动不大,基本上呈现较为稳定的板块关联态势,这也意味着如果按照上述板块关联特征制定详细的产业协同减排政策,后期因网络结构变动带来的政策调整成本较小.
3 中国工业碳排放网络的链路预测
3.1 参数确定与预测模型精度分析
为了使模型更加精确,首先进行模型精度检验.基于上文预测模型,利用1997、2002、2007、2012年的碳排放有向加权网络作为训练集,并以2017 年中国工业碳排放实际网络作为验证集,进行精度检验.在模型精度分析中,采用常用的AUC(Area Under Curve)值作为模型精度的判别标准.AUC 能在整体上衡量算法的精确度,在信号探测理论中是指ROC(Receiver Operating characteristic Curve)曲线下的面积[33].同时,参照王斌等[31]的做法,参数(r、δ、η、θ)的具体取值在AUC 值最大时确定.
首先利用公式(12)与1997~2012 年的投入产出数据计算得到每条弧在2017 年的预测得分.由于本文的工业碳排放网络节点数较少,属于小规模网络,为更好检验预测模型精度,这里采用逐项遍历的方法逐次验证每条弧的精度.也即每次从2017 年实际碳排放网络的已知弧集中选取1 条弧做为测试弧,将这条弧的预测分数值与2017 年实际碳排放网络中每条不存在的弧的预测分数值做比较,这样共有n = U −E 次比较,其中U 为网络中理论上可能存在的弧的集合,E 为实际网络中存在的弧的集合.如果测试弧的预测分数值大于不存在的弧的预测分数就加1 分,如果两个预测分数值相等就加0.5 分,其他情况下取0 分.这样比较n 次,如果有n′次测试集中的弧的分数大于不存在的弧的分数,有n′次两个分数值相等,则AUC 的公式如下[34]:
显然,AUC 值越接近1,模型精度越高.最后遍历网络中的每条已知弧,并计算已知弧集AUC 值的平均值,作为整个2017 年预测网络的精度值.此外,在求解类似最优化问题中,相较于传统梯度下降算法,由于模拟退火算法具有更强全局优化能力,对问题中的噪声和不确定性具有一定鲁棒性,并且更适用于解空间具有复杂结构的问题;而与遗传算法或粒子群优化算法等其他优化算法相比,模拟退火算法具有不需要进行大量人为参数调优的优势.这里采用模拟退火算法在各参数(r、δ、η、θ)的取值范围里进行最优化搜索,来获得各参数的最优取值.设置各参数的精度为10-4,迭代次数为105,得到r、δ、η、θ的最优取值分别为0.847、-0.542、0.542、0.888,此时模型的AUC值为0.939.为进一步检验精度的稳定性,使用1997、2002、2007 年的实际网络为训练集,以2012 年的实际网络作为验证集,考量了该方法在2012年数据应用上的预测精度,结果显示AUC 值仍然达到了0.902.总体而言,模型预测精度具有一定的稳定性,而且这也一定程度上说明了随着该预测模型的训练集增加,模型的预测精度进一步增加.
3.2 链路预测结果
利用上述求得的各个最优参数以及1997~2017年的中国工业碳排放网络信息,计算2022 年30 个行业之间的每条弧的得分值,得到一个30×30 的矩阵,该矩阵的第i 行第j 列表示2022 年时行业i 对行业j 存在碳排放关联的可能性大小得分(得分越高,可能性越大).以1997、2002、2007、2012、2017 年5个年份网络数据为基础,得到预测的2022 年中国工业碳排放的有向无权网络,并采用整体网和个体网以及块模型分析方法计算2022 年的各类指标值.
从2022 年整体网络特征来看,中国工业碳排放网络的密度有显著下降趋势,仅为0.271,说明中国工业碳排放网络行业之间联系紧密程度有所下降;网络关联度出现下降,打破了在2002~2017 年之间长期维系在1.000 的局面,在2022 年为0.933,这说明2022 年的碳排放网络的连通性出现了下降,出现了被孤立的行业;而网络等级度下降到了0.133,说明越多的行业处于网络核心地位,越少的行业在碳排放关联网络中处于从属和边缘地位;网络效率在2022年达到了新高的0.527,说明行业之间链路变少,行业之间碳排放网络越来越稀疏.上述整体网络特征的结果表征着2022 年的工业碳排放网络复杂性进一步增加,行业间割裂地实施自身行业碳减排策略,将使得我国工业整体减排的难度进一步增大.
从2022 年的个体网络特征来看,中国工业碳排放网络的入度值、出度值、中介中心性、接近中心性等预测值及其与2017 年相比较的变动值如表4所示.因2022 年网络密度的减少,大部分行业部门的出度值与入度值都呈现了下降趋势,其中出度值增加的行业部门为木材加工及家具制造业(IND09)、燃气生产和供应业(IND29)、交通运输设备制造业(IND23)3 个部门,入度值增加的行业部门主要是仪器仪表、文化办公用机械制造业(IND26)、其他制造业(IND27)、煤炭采选业(IND01)、黑色金属矿采选业(IND03)4 个部门.而中介中心性与接近中心性出现了反方向变化的趋势,绝大多数行业部门的接近中心性出现下降趋势,绝大多数行业部门中介中心性则出现了上升趋势.出现这种现象的原因在于,虽然二者都从不同角度代表了行业部门在整个碳排放网络中的“核心”地位,但中介中心度代表了该节点对网络中节点对之间捷径控制的概率,而本文接近中心度则代表该节点与其他节点之间捷径距离之和呈反比例关系,因此这种现象是由于2022 预测网络密度显著下降的同时,各个行业在网络中地位越来越均势导致的.具体来看,接近中心性除了仪器仪表、文化办公用机械制造业(IND26)相较于2017年增加了0.029外,其他行业都出现了下降趋势.相较于2017 年,2022 年的中介中心性表现为自然资源采选业(IND01~05)、 金属加工与制品业(IND18~20)以及机械与设备制造业(IND21~27)3 大板块的上升趋势.并且这其中机械制造业(IND21~27)的中介中心性上升是伴随着这些行业的出度与入度值下降趋势,这说明机械与设备制造业(IND21~27)的“自我”少数关系对于中国工业整个碳排放关联网络的碳流动来说至关重要.此外,石油加工及炼焦业(IND12)、化学原料及化学品制造业(IND13)、黑色金属冶炼及压延加工业(IND18)、普通机械制造业(IND21)、交通运输设备制造业(IND23)的中介中心性与接近中心性都排在了前5 位,最新的产业协同碳减排政策应当给予更多关注,要充分发挥这5 个行业所扮演的“中心行动者”和“桥梁”作用.
从2022 年的板块结构来看(图4),板块间关联关系从2017 年的5 条链路上升到了2022 年的6 条链路,碳排放网络的板块间关联关系也进一步复杂化.其中,相较于2017 年的板块关联关系而言,板块I 的内部关联密度从2017 年的0.622 下降至0.393,而板块I 至板块II 的碳溢出效应也从不显著变为显著,板块II 在板块结构中的角色也从净溢出板块变为“经纪人”板块.从板块的成员构成来看,煤炭采选业(IND01)、食品与饮料制造业(IND06)、纺织业(IND08)、橡胶和塑料制品业(IND16)、有色金属冶炼及压延加工业(IND19)5个行业成为了第II板块成员,行业部门的中介属性增强.而针对于板块II“经纪人”属性的变换,对于板块II 的行业成员而言,不仅要控制其碳吸入程度,也要控制其自身能耗强度,进而减少其向其他行业的碳溢出.
4 政策启示
工业碳关联网络有着复杂的网络结构形态,为实现“双碳”目标,在碳减排政策的制定、完善和实施过程中,不仅要考虑行业部门碳排放“量”的数据表现,更要注重行业部门之间碳关联“关系”的效应.要重视发挥碳排放关联网络节点特征对跨行业协同减排的作用,由于样本期内没有高碳溢出效应与高碳吸入效应同时存在的行业部门,因此要对机械与设备制造的5 个高碳吸入下游行业部门(IND20-IND25)以及黑色金属冶炼及压延加工业、化学原料及化学品制造业与石油加工及炼焦业等碳溢出效应明显的上游行业部门进行分类定向调控,在精准降低这些部门自身碳排放量强度的同时,也要通过跨部门协同碳减排政策降低产业链前后向碳关联强度.一方面可通过减排能力、成本等因素的综合平衡来确定上下游行业部门的减排比例,另一方面也可以借助碳交易市场,给予碳溢出效应显著的上游行业部门更多的初始配额,通过市场配额交易降低上游行业部门因中间产品的输出而需要额外提供的碳减排成本.
虽然中介中心性与接近中心性的测度内涵稍有差别,但其值越大一定程度上都代表着其越居于网络的“核心”地位,抑或是代表着这些行业部门在网络中控制资源的能力越强.因此在碳减排过程中,要充分利用中介中心性与接近中心性值都较高的黑色金属冶炼及压延加工业、化学原料及化学品制造业、普通机械制造业、交通运输设备制造业与石油加工及炼焦业的关键行业部门在中国工业碳排放关联网络中所起到的“桥梁”作用和所扮演的“中心行动者”角色,通过碳排放的部门间传导网络将先进的减排技术与信息扩散到产业链上下游行业.特别是链路预测结果显示,机械与设备制造业(IND21-27)表现出了“自我”少数碳关联关系对于网络碳流动重要影响的关键特征,因此我国最新的减排资金安排和碳减排激励政策中应优先考虑上述部门,以保证中国工业碳减排的整体效果.
行业部门间的协同减排要充分捕捉利用碳关联网络中聚类特征与碳转移路径等信息,制定具有差异化的行业部门分类管理政策,以达到节约减排成本与提高减排效率的效果.对于金属与非金属采选业等部门组成的“溢出”板块,应当更加注重技术进步带动其直接碳排放强度的下降,从根本上减少其对其他行业的传导作用.对于“受溢”板块,应寻找其主要流入源头,一方面可以通过合理制定行业中间品采购标准的方式,倒逼上游行业改进相关技术,以减少碳吸入;另一方面也可以尝试寻找替代品进而减少碳流入量,以达到降低碳排放量的目标.而无论是“双向溢出”还是“双向受溢”板块,都代表着板块内部成员之间有着显著的碳关联关系存在,因此这两个板块的行业部门需要共同承担减排责任,可以考虑为这些行业部门制定组团减排政策.此外,针对于“经纪人”板块,不仅要控制碳吸入程度,同时也要减少自身能耗强度,加大清洁能源使用比例,从源头上减少其碳排放量,进而减少其向其他行业的碳溢出量.
5 结论
5.1 从网络结构特征上看,中国碳排放关联网络密度基本呈现逐年提高的趋势,,工业各部门之间的碳排放具有普遍的碳关联和碳溢出效应.有50%的行业部门属于“低入度—低出度”特征部门,机械与设备制造职能的5 个工业部门(IND20-IND25)发挥碳吸入作用显著,黑色金属冶炼及压延加工业、化学原料及化学品制造业与石油加工及炼焦业的碳溢出效应明显.普通机械制造业、化学原料及化学品制造业与黑色金属冶炼及压延加工业等行业部门在整个工业碳排放关联网络中体现出较强的“桥梁”作用.黑色金属冶炼及压延加工业、化学原料及化学品制造业与石油加工及炼焦业等行业部门在网络中扮演“中心行动者”角色.
5.2 块模型分析结果显示,能源开采部门(IND01-02)与基础工业部门(IND10、12、13、15~19、28)等部门组成的板块I 在网络中扮演“双向溢出”角色,主要金属矿采选业(IND03~04)与非金属矿采选业(IND05)等组成的板块II 在网络中扮演“溢出”角色,机械制造业(IND21~27)与部分轻工业(IND06、08、09)等部门组成的板块III 在网络中扮演“双向受溢”角色,燃气生产和供应业、自来水的生产和供应业以及部分轻工业(IND07、11、14)等部门组成的板块IV 在网络中扮演“净受溢”角色.
5.3 链路预测的结果显示,2022 年的中国工业碳关联网络密度显著下降,而越多的行业处于网络核心地位.黑色金属冶炼及压延加工业、化学原料及化学品制造业、普通机械制造业、交通运输设备制造业与石油加工及炼焦业的中介中心性与接近中心性都排在了前5 位,而机械与设备制造业(IND21~27)的中介中心性上升的同时却伴随着这些行业的出度与入度值下降,这说明机械与设备制造业(IND21~27)的“自我”少数关联关系对于中国工业整个碳排放关联网络的碳流动来说至关重要.2022 年中国工业碳关联板块结构进一步复杂化,煤炭采选业、食品与饮料制造业、纺织业、橡胶和塑料制品业、有色金属冶炼及压延加工业5 个行业部门的中介属性增强.

