基于乘客服务水平和安全的城市轨道交通扣车方案评价*

江志彬 来佳雯 赵 源,3 王智永 金碧筠

(1.同济大学道路与交通工程教育部重点实验室, 201804, 上海; 2.上海市轨道交通结构耐久与系统安全重点实验室,201804, 上海; 3.上海申通地铁集团有限公司运营管理中心, 201100, 上海; 4.苏州市轨道交通集团有限公司, 215558,苏州; 5.上海申中轨道交通运行安全工程技术研究有限公司, 201204, 上海)

城市轨道交通系统在复杂多变的环境下,如运营设施与设备故障、客流突变,以及极端天气、突发事件等不可预计的外部因素下都有可能导致列车产生运行延误,其最直接的表现是运营成本和乘客出行时间的增加,以及线网输送能力和运营效率的下降,严重情况下还会造成生命财产损失[1]。

列车运行调整是在发生列车运行干扰时,选择有效方案进行列车运营调度,以尽快消除干扰,降低列车运行延误对乘客出行的综合影响,提高线网的运营安全和可靠性[2]。列车运行方案的选择与列车运行延误的程度有关:当延误程度较小时,可以利用列车运行图缓冲时间,通过缩短停站时间、区间运行时间等手段恢复列车正点运行;当延误程度较大时,需要采取跳停、扣车、加开备车、小交路折返等单一或组合措施对列车运行进行调整[3-4]。在上述方案中,扣车是在发生长时间的初始延误条件下经常采用的列车运行方案。

扣车方案的选择受乘客出行OD(起讫点)、列车均衡性、站台安全及服务水平等综合因素的影响。在制定具体方案时,既要考虑尽量减少受延误影响的列车数量和范围,更要考虑乘客的服务水平和站台的聚集风险。既有成果多从单一的列车影响的角度来考虑,对于运营现场的指导作用有限。本文构建了基于乘客服务和安全的扣车方案评价模型,并以某城市轨道交通线路的实际客流数据为实例,对不同的扣车方案进行评价。

1 城市轨道交通扣车方案

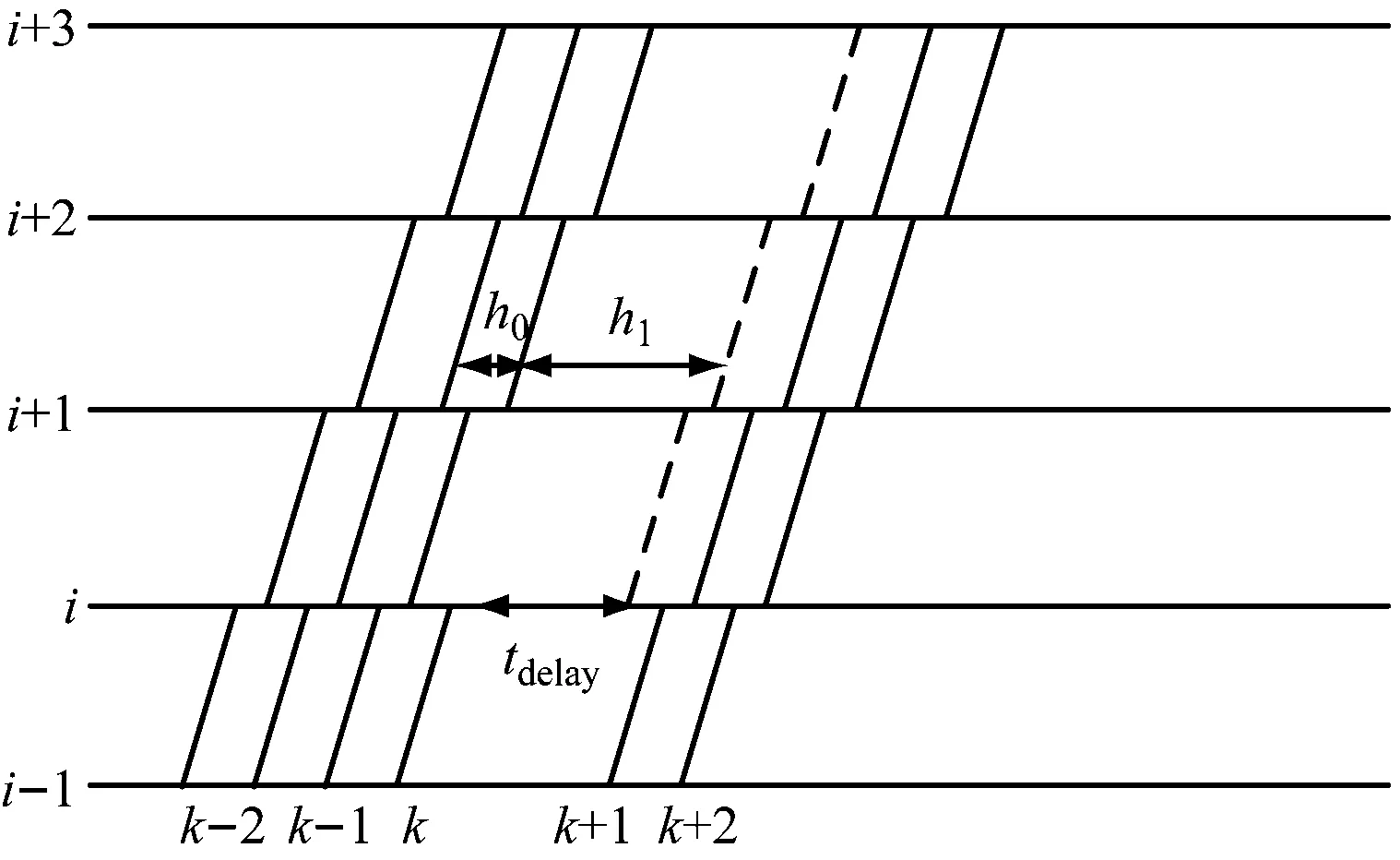
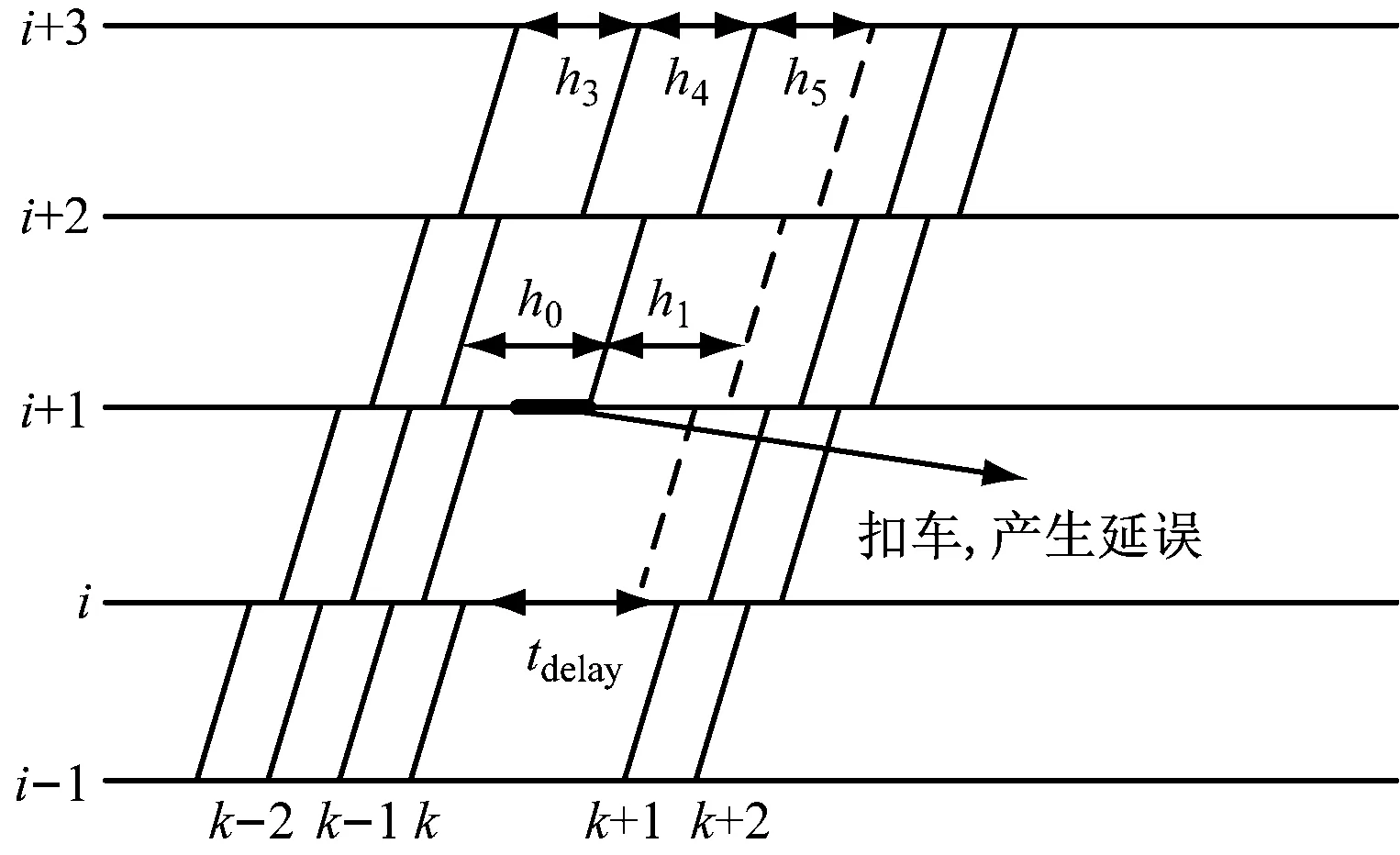
扣车是指发生长时间延误时,延长前行部分列车在前方部分车站的停站时间,延迟发车时刻,以均衡部分列车间行车间隔的调整方案。扣车方案示意图如图1所示。图1中,h0、h1、h3、h4、h5分别代表不同车站的发车间隔。列车k在车站i发生延误,延误时间过长时,可以通过前行列车在相应的车站扣停来调整发车间隔。如:列车k-1在车站i+1和i+2延长停站时间,列车k-2在车站i+2延长停站时间,均衡车站i+1和i+2的发车间隔,避免发车间隔过大造成车站i+1的客流聚集。

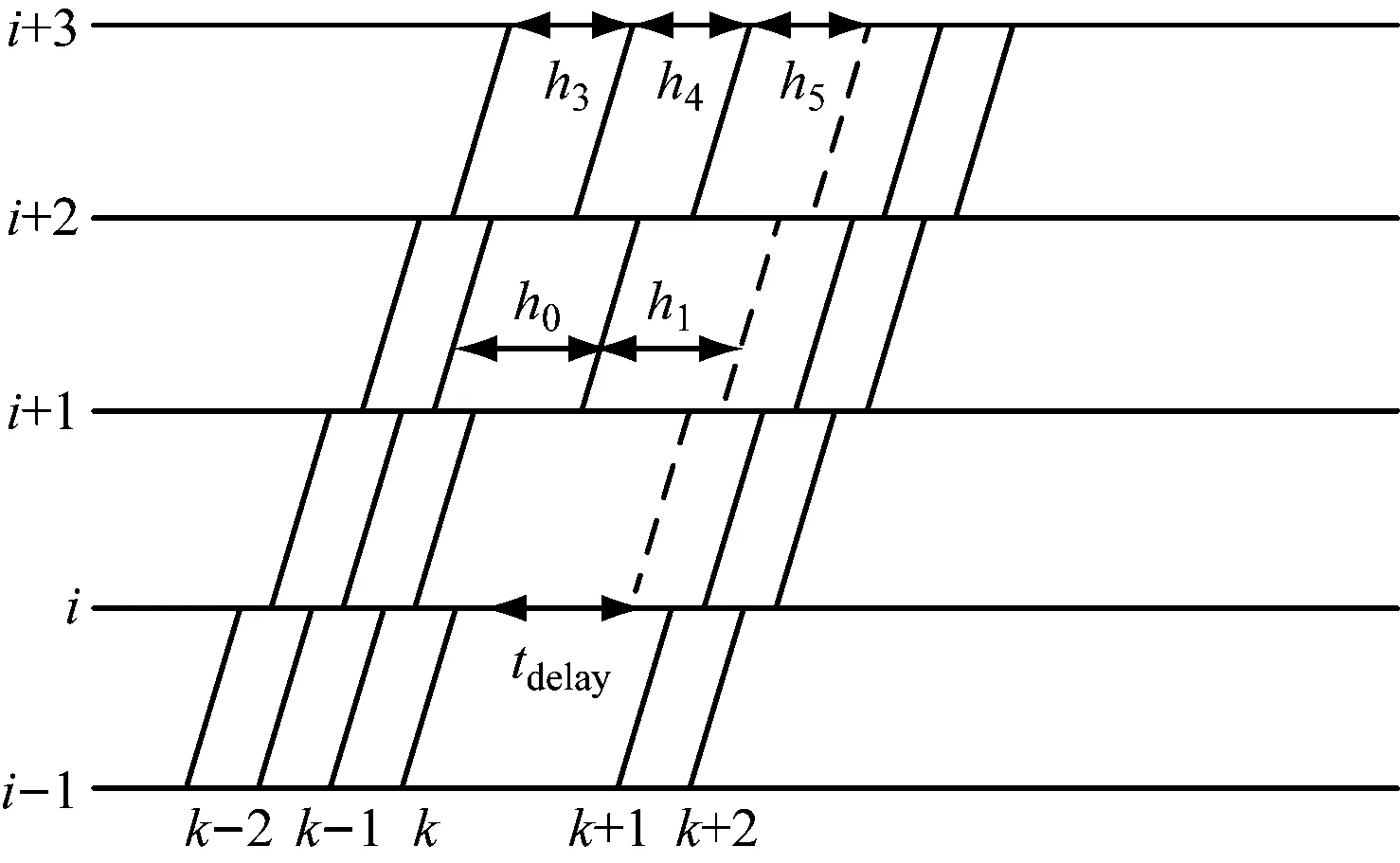
注:i-1、i、i+1、i+2、i+3—车站编号;tdelay—延误时间;k-2、k-1、k、k+1、k+2—列车编号。

扣车方案可以缩短部分乘客在车站的候车时间,提高列车服务间隔的均衡性,降低因乘客滞留带来的聚集风险,但扣车会增加部分车内乘客的旅行时间。扣车方案的选择是一个组合优化问题,需要在有限时间范围内决定所扣列车、扣车车站、扣车时长等问题。相同初始延误条件下通常有多种扣车方案。

2 基于乘客服务和安全的扣车方案评价模型

2.1 列车延误类指标

2.1.1 最大发车间隔

列车发生初始延误后,车站的发车间隔也会相应增大。列车运行调整后的最大发车间隔一定程度上反映了调整措施的服务水平,以及可能存在的安全隐患。最大发车间隔Hmax为:

Hmax=max(h)

(1)

式中:

h——发车间隔。

2.1.2 列车总延误时间

列车总延误时间表示实际运行图与计划运行图相比,所有列车的出发与到达延误时间之和,可以反映实际运行图与计划运行图的偏差大小。列车总延误时间td为:

(2)

式中:

R——列车总数;

M——车站总数;

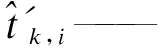
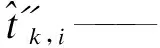
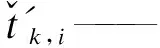
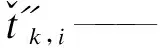
2.1.3 列车均衡性

列车均衡性是衡量列车运行效果的重要指标之一,列车延误可能会导致某站相邻列车到站间隔增大,均衡性降低:列车行车间隔过大时,乘客候车时间增加,容易造成客流聚集,引发安全风险;而列车行车间隔过小时,可能会导致前行列车刚驶离站台,后行列车紧至,从而造成后行列车运力的浪费[5]。列车均衡性为:

(3)

其中:

(4)

(5)

式中:

Da——运行图中的列车均衡性;

hk,i——列车k和k+1在车站i的发车间隔;

Di——车站i的列车均衡性;

Ei——车站i列车出发间隔的均值。

式(3)中,Da取值越大,说明发车间隔分散程度越高,均衡性越差;Da取值越小,说明发车间隔分布越均匀,均衡性越好。

2.1.4 终到延误列车数

终到延误列车数是指受到终到延误影响的列车数。当列车在终到站的实际到达时刻与计划到达时刻偏离时,即认为该趟列车延误。终到延误列车数Vd为:

(6)

其中:

(7)

式中:

ts——偏离标准。

2.2 乘客服务和安全类指标

2.2.1 滞留乘客数

城市轨道交通列车延误的影响范围广,影响人数多,容易造成乘客在车站的拥堵,威胁公共安全水平。因此,站台滞留乘客数是判断列车运行调整措施在安全性方面的重要标准之一,由列车车厢内乘客数、该站上车人数、该站下车人数,以及列车载客能力等因素综合决定。滞留乘客数Sq为:

(8)

式中:

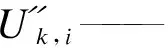
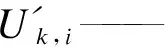
2.2.2 乘客总旅行时间

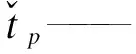
乘客总旅行时间是指所有乘客的旅行时间之和。将受到列车运行延误影响的乘客分为两部分:一是车厢内乘客,二是车站候车乘客。对于车厢内的乘客而言,运行延误必然会导致其在车内旅行时间的延长,造成的影响是负面的;而对于车站候车的乘客,延误的影响有可能是正面的,因为在延误时间段内到达的乘客,前行到达列车延误使得这些乘客也可以乘坐延误列车,反而减少了候车时间[6]。因此,选择使用所有乘客旅行时间之和这一指标,更能反映列车运行调整措施对所有乘客的总体影响。乘客的总旅行时间tp为:

(9)

式中:

P——乘客总数;

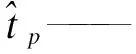
2.3 综合评价指标

由于扣车方案是一个多目标决策问题,需要构建综合评价指标对调整方案进行评价。由于各指标的计量单位不同,在计算综合指标前,需对各指标进行标准化处理:

(10)

式中:

amn——第m个方案中第n个指标取值;

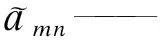
将标准化处理后的指标取值乘以指标权重,计算得到各方案的综合评价指标取值。

(11)

式中:

Zm——方案m的综合评价指标;

N——评价指标总数;

wn——指标n对应的权重。

本文所设指标包括最大发车间隔、列车总延误时间、列车均衡性、终到延误列车数、滞留乘客数及乘客总旅行时间等6个,均为负向指标,即指标取值越小,列车运行调整方案的效果越好。

2.4 综合评价指标的计算流程

扣车方案的指标计算流程较为复杂,需基于调整方案,综合考虑乘客OD、计划运行图、初始延误时间、列车能力及站台能力等约束,模拟列车与乘客的交互过程,以及每位乘客的实际乘车过程,最终得到各类指标。详细的计算流程如图2所示。

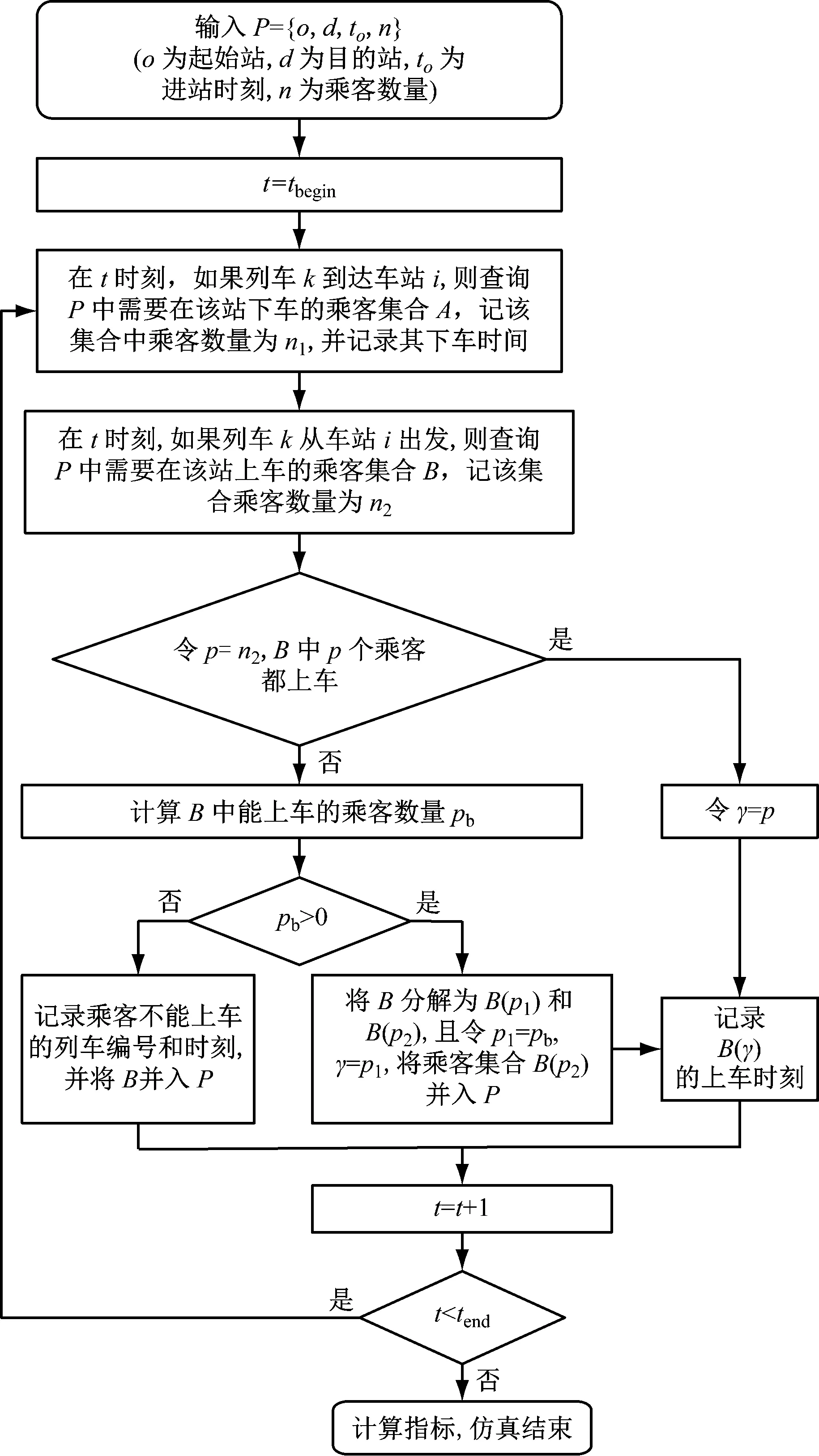
注:tbegin—仿真设计的开始时间;tend—仿真设置的结束时间。

3 案例分析

3.1 基本假设

本文选取上海某条轨道交通线路的4个区间,以早高峰小时的实际OD客流量数据为例进行计算。假设列车在车站发生延误,延误时间为20 min,列车最小追踪时间为2 min 30 s,计划在站停车时间为30 s,列车载客能力为2 000人。计算过程中,终到延误列车数的ts取1 s,站间运行时间均假设不发生改变。

车站的发车间隔受该站列车扣车时间的影响,改变扣车时间可以改变该车站的发车间隔。在本算例中,通过改变列车k-2在车站i+2的扣车时间,以及列车k-1在车站i+1及i+2的扣车时间,可以得到不同的扣车方案。列车运行调整方案示意图如图3所示。上海某条轨道交通线路OD客流量见表1,常用的扣车调整方案见表2。

a) 不采用扣车方案

b) 采用扣车方案

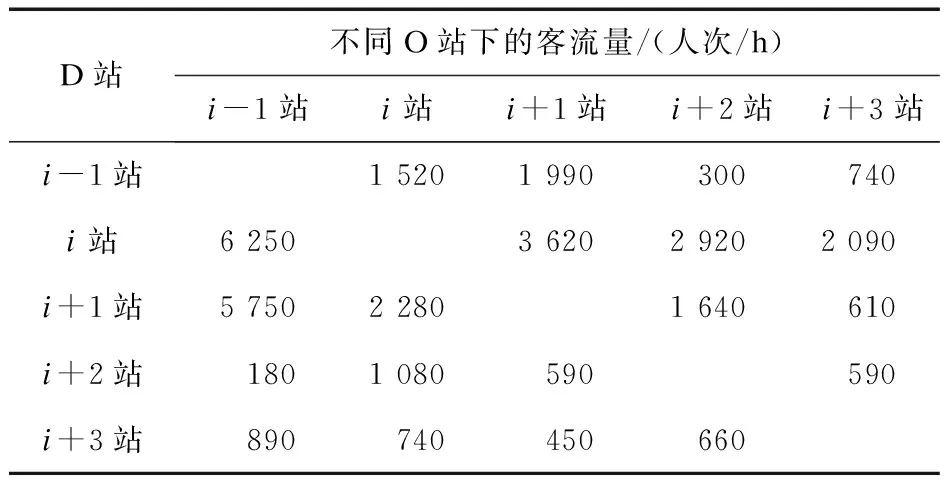
表1 上海某条轨道交通线路OD客流量

表2 上海某条轨道交通线路扣车调整方案

3.2 计算结果

制定扣车调整方案时,重点考虑乘客服务与安全因素,本算例将Hmax、td、Da、Vd、Sq及tp的权重分别取为0.1、0.1、0.2、0.1、0.3和0.2。各方案的综合评价指标计算结果如表3所示。由表3可见:方案6下的综合评价指标最小,为最优方案。

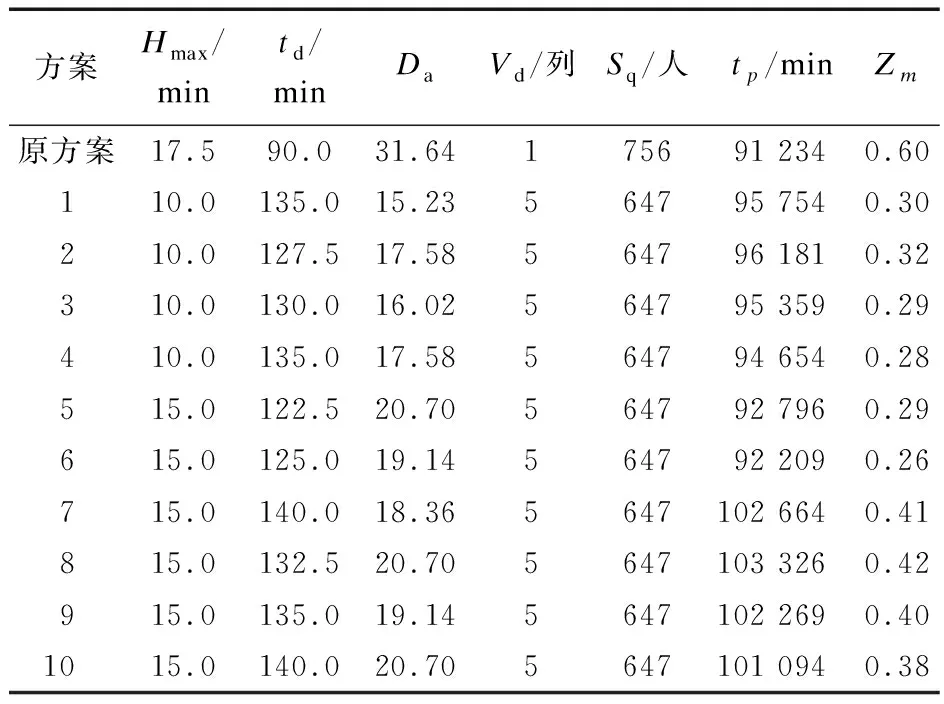
表3 各方案下的综合评价指标

3.3 结果分析

在评价扣车调整方案时,侧重点不同会影响最终的评价结果。例如,若重点考虑列车均衡性这一指标,方案1的调整效果最好。原因在于方案1通过合理安排列车的在站扣车时间,使得车站的发车间隔趋于相等,提高了列车运行图的均衡性。若重点考虑乘客总旅行时间这一指标,则不采取扣车措施时效果最好。但不采取调整措施时列车的发车间隔过大,列车均衡性降低,容易造成站台乘客滞留,增加安全隐患,并影响乘客的出行体验。从综合评价指标来看,方案6为最优方案,其行车间隔分别为h0=10 min、h3=5 min、h4=10 min。此方案下对应调整后的列车运行图如图4所示。

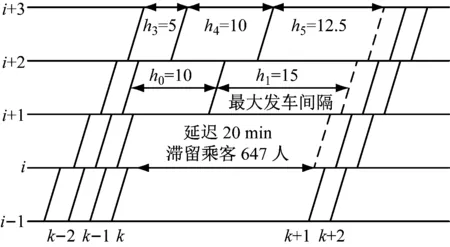
时间单位:min

4 结语

本文构建了考虑最大发车间隔、列车总延误时间、列车均衡性、终到延误列车数、滞留乘客数及乘客总旅行时间的扣车方案综合评价模型,并通过实际案例进行了量化分析。结果表明,虽然扣车措施会延长部分乘客的在站停站时间,造成乘客总旅行时间的增加,但可以有效提高列车运行图的均衡性,减少滞留乘客的数量,降低车站的安全隐患。在实际运营过程中,如何基于复杂的线路和客流条件,在不同的初始延误地点和时间条件下寻求一个较优的扣车调整方案,以及更加客观有效地确定各评价指标权重还有待进一步研究。