移动性感知下基于负载均衡的任务迁移方案*
鲜永菊,韩瑞寅,左维昊,汪帅鸽
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
随着移动通信技术和物联网产业的不断发展,以虚拟现实(Virtual Reality,VR)、增强现实(Augmented Reality,AR)、自动驾驶、远程医疗为代表的一系列新型业务产生,给人们的生活带来了全新的体验。这类业务往往具有较大的计算需求和较高的时延敏感度,给能量、计算资源有限的移动终端设备带来了极大挑战。移动边缘计算(Mobile Edge Computing,MEC)将原本云计算的计算资源和存储资源下沉到更靠近用户一侧的边缘设备上,能够为用户提供低时延高可靠性的服务,提升用户服务质量(Quality of Service,QoS)。
用户的移动性作为MEC环境中一项不可忽略的因素,极大限制了用户服务质量的提升。用户移动过程中,信道状态会不断变化,可能会影响原有卸载方案性能。通过跟随用户移动进行任务迁移的方式,可以在一定程度上保证用户QoS和服务连续性[1]。但在这一过程中,大量用户的涌入或者离开引发的任务迁移,会使得服务器负载突然增加或者减少,导致整个系统中负载分布不均,增加用户任务在部分服务器上的排队时延,导致系统资源利用不均,降低系统吞吐量[2]。因此,如何在保证用户服务连续不中断的前提下,进行卸载和迁移决策,保证系统负载均衡,是MEC任务迁移中一项亟待解决的问题。
针对边缘计算中用户移动性导致的QoS下降的问题,部分文献采用凸优化或者启发式算法进行求解。文献[3-4]提出的方案均未考虑移动性可能带来的负载分布不均的问题,文献[5-6]提出的方案只进行了单时隙优化,没有考虑到系统长期性能优化。
近年来,随着强化学习的兴起,也有大量文献采用强化学习方法进行研究[7-9],但这些研究都是基于单智能体强化学习算法进行求解,只适用于控制器集中控制或者单个用户决策的场景。还有文献是基于多智能体强化学习(Multi-agent Reinforcement Learning,MARL)进行研究的。文献[10]建立了多用户场景下的任务迁移模型,采用基于反事实多智能体(Counterfactual Multi-agent,COMA)的分布式任务迁移算法求解原问题,但是作者假设所有任务均已卸载,忽略了卸载决策和资源分配的影响。文献[11]采用多智能体深度Q网络(Deep Q Network,DQN),使用双分支卷积神经网络生成任务迁移和移动决策。
综上所述,目前已有大量研究工作围绕移动性场景下用户任务迁移展开,但是少有研究关注用户移动性带来负载分布不均的问题。此外,在多用户多基站的分布式场景下,采用集中式控制需要不断收集用户位置变化信息,这会产生较大的信令收集成本。因此,本文提出了一种基于多智能体柔性演员-评论家(Soft Actor-Critic,SAC)的分布式任务迁移方案(Distributed Soft Actor-Critic Migration,DSACM)来解决上述问题,具体的研究工作可以概括如下:
一是建立了多用户多节点MEC场景下用户随机移动的任务迁移模型,将其建模为一个长期极大极小化公平性问题,旨在考虑系统迁移成本约束、用户设备能耗约束和系统负载均衡的同时,优化性能最差的用户的服务质量。
二是通过引入辅助变量结合李雅普诺夫(Lyapunov)优化的方式将原问题转化并解耦,将其建模为去中心化部分可观测马尔可夫决策过程(Decentralized Partially Observable Markov Decision Process,Dec-POMDP),将奖励函数分解为节点全局奖励和用户个体奖励,分别基于网络负载和用户QoS对用户动作施加奖励。
三审针对集中式控制需要大量收集用户信息的问题,提出一种基于扩展多智能体SAC的分布式任务迁移方案。利用集中式训练分布式执行(Central Training Distributed Execute,CTDE)框架,将单智能体强化学习算法SAC扩展到多智能体领域。相比于一般的强化学习算法,SAC算法通过最大化熵正则项可以获得更高的探索能力和更强的鲁棒性。
1 系统模型
1.1 网络模型
在图1所示的系统模型中,每个小基站上部署一个服务器,不同小基站上的服务器计算能力异构,一共有M个服务器,M={1,2,…,m,…,M}表示服务器的集合。系统中共有U个用户,用户集合用U={1,2,…,u,…,U}表示,用户设备可以是车辆、普通移动用户等。假设每个用户在关联节点上都有一个虚拟机提供服务,它可以跟随用户移动被迁移到新的服务器上继续执行。
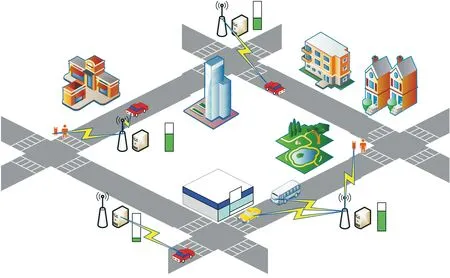
图1 系统模型Fig.1 System model


1.2 通信模型

(1)

(2)
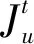
(3)
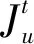
(4)

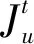
1.3 计算模型
1.3.1 本地计算
当任务本地执行时,即使用户位置发生改变,任务仍然在本地设备上继续执行,用户设备能耗只包括本地计算能耗,本地计算时延可以表示为
(5)

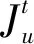
(6)
式中:κ是与芯片架构相关的有效能量成本系数。
1.3.2 边缘计算
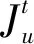
(7)
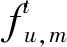
整个边缘执行阶段包括用户将任务发送到服务器,服务器完成任务计算,计算结果发送给用户三部分。其中,由于任务输出结果往往较小,且下行链路传输速率较快,因此这一部分时延可以忽略。任务在边缘执行的总时延可以表示为
(8)
1.4 任务迁移及用户QoS模型
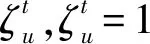
(9)
任务迁移通过服务器间的有线连接完成,为了简化计算,基于静态路由跳数计算有线传输时延。使用Q表示单跳时延,σi,j表示服务器i与服务器j之间的路由跳数,任务的迁移时延可以具体表示为
(10)

(11)
式中:C是固定的迁移成本;b是控制因子,用于控制迁移成本随待迁移用户数变化的快慢。
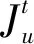
(12)
t时隙内,所有用户产生的总迁移成本可以表示为
(13)
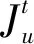
(14)
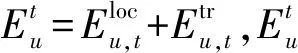
用户QoS与任务完成时延相关,用户QoS模型可以利用对数函数规律进行刻画[8]。用户QoS增益可以表示为
(15)
1.5 负载均衡模型
为了衡量用户移动过程中网络负载变化情况,受文献[12]的启发,服务器的负载状态可以用服务器的剩余CPU和存储资源来刻画。定义t时隙服务器m的负载为
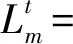
(16)
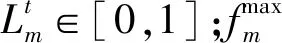

2 问题建模
通过联合优化用户卸载策略、迁移决策和计算资源分配,优化性能最差的用户平均QoS,长期优化问题建模为
(17)
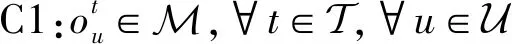

2.1 引入辅助变量
由于建模的是一个长期极大极小化公平性问题,难以直接求解。根据文献[13]和文献[14]中的方法,可以每个时隙引入辅助变量φt,将其转化为一个最大化问题。P1可以被等价转化为P2,具体表示如下:
(18)
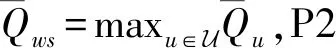
2.2 李雅普诺夫优化

(19)
针对约束条件C5,定义虚拟迁移成本队列G(t),表示t时隙内系统中所有用户产生的迁移成本:
(20)
针对引入的辅助变量约束条件C7,定义虚拟队列Y(t)={Yu(t)}u∈U,虚拟队列的动态变化表示如下:
Yu(t+1)=max{Yu(t)+φ(t)-Qu(t),0}
(21)
为了联合控制能耗队列和迁移成本队列,定义Θ(t){Z(t),Y(t),G(t)}作为总队列积压。定义李雅普诺夫函数L(Θ(t))如下:
(22)
定义两个时隙间李雅普诺夫函数的变化为李雅普诺夫漂移函数ΔL(Θ(t)),为了保证队列的稳定,需要最小化漂移函数的值,ΔL(Θ(t))表示如下:
ΔL(Θ(t))=E{L(Θ(T+1))-L(Θ(t))|Θ(t)}
(23)
定义李雅普诺夫漂移加惩罚项为
Λ(Θ(t))ΔL(Θ(t))-VE{φt|Θ(t)|}
(24)
式中:V(V>0)是控制因子,用于控制队列稳定性与目标函数优化之间的权重。惩罚项可以表示为目标函数的映射,加上这一项是为了在最小化李雅普诺夫漂移保证队列稳定性的同时最小化目标函数的值。
可以得到李雅普诺夫漂移函数ΔL(Θ(t))表示为
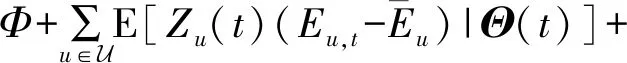
(25)

为了在最大化用户QoS的同时保证队列积压Θ(t)的稳定,采用最小化李雅普诺夫漂移加惩罚项的方式,可以得到
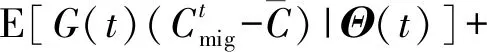
(26)
优化问题P2可被进一步转化为
s.t.C1,C2,C4,C8
(27)
3 基于SAC的分布式任务迁移方案
3.1 去中心化部分可观测马尔可夫决策过程
强化学习可以适应复杂的环境状态变化,但对于大规模分布式系统,单一智能体要学习大量分布式策略,随着策略网络数量的增加,会使得状态空间呈指数级增长。将单个庞大的智能体分解为多个结构简单的智能体,可以降低状态空间和动作空间的维度[15]。
在本文中,大量移动用户的存在使得集中式控制器难以及时收集到所有用户的信息,容易出现状态空间“维度爆炸”的现象。因此,本文采用MARL方式,由每个用户设备作为智能体进行决策。对于每一个用户智能体U-Agent而言,难以获得完整的网络状态和其他所有智能体的动作,用户进行决策时只能够观测到部分环境状态。借助Dec-POMDP理论,可以将这一过程建模如下:
观测空间:对于智能体U-Agentu,状态包括剩余可用迁移成本预算、剩余设备能量、节点剩余计算资源、当前负载偏差值等。观测空间定义为
(28)
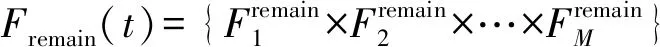
动作空间:动作空间包括卸载决策、服务器关联策略、功率分配策略,定义为
Au(t)={ρu(t),ou(t),pu(t)}
(29)
奖励函数:以往相关文献研究中奖励函数往往设置为共享的全局奖励,但在多智能体场景下,难以衡量某一个智能体对全局奖励的贡献值,容易产生信用分配问题。在这种情况下,部分智能体无法得到有效训练。受文献[16]的启发,本文将奖励函数分别设置为节点全局奖励函数和个体奖励函数。对于边缘节点而言,希望能够在保证用户QoS的同时,维持整个网络的负载均衡。节点基于当前自身负载均衡度和剩余迁移成本预算队列建立全局奖励函数,避免只考虑用户移动性进行任务迁移容易导致的负载不均衡问题。节点m处的全局奖励函数可以表示为
(30)
式中:ω作为归一化因子。
用户智能体需要关注自身QoS与能耗,结合优化问题P3的优化目标,因此可以将个体奖励函数表示为
(31)
3.2 DSACM算法
本文采用CTDE框架,借助以往收集数据对网络进行预训练,之后直接将训练好的模型分发给参与卸载的用户,用户直接离线执行任务。在线执行阶段,用户智能体只需要依靠自身局部环境观测就可以做出实时性决策[17]。DSACM网络结构如图2所示。

图2 DSACM网络结构Fig.2 DSACM network structure
由于用户在系统中随机移动以及信道时变特性,导致网络状态不断发生变化。为了稳定算法收敛过程,本文将单智能体SAC扩展到多智能体领域。SAC是一种离线强化学习算法,通过最大化熵正则项来做出更加随机的决策,增加算法的探索性能,避免陷入局部最优解。相比于一般的最大化奖励的强化学习算法,SAC有着更高的探索能力和更强的鲁棒性,能够更好地适应复杂的网络环境[18]。
针对本文中多用户多节点的分布式场景,所提分布式SAC算法训练的目标是最大化如下所示的熵正则项:
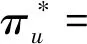
(32)
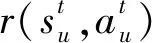
在Actor-Critic网络架构中,长期训练过程时,为了最大化长期回报奖励,需要借助Critic网络和Actor网络对策略进行评估和改进。用户价值网络软Q值函数为
(33)

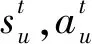
(34)
为了避免价值网络输出的Q值出现高估问题,引入双Q网络,使用两个网络中Q值最小的一个作为近似估计值,即有

(35)
同理可以得到节点价值网络损失函数。采用梯度下降法更新用户智能体和节点处的价值网络,用户价值网络更新公式可以表示为
(36)
节点价值网络更新公式为
(37)
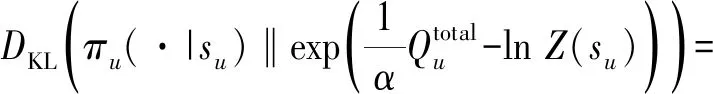
(38)
所提出的DSACM算法具体描述如下:
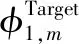
1 for episodet=1 to MAX_EPISODE do
2 生成随机数p∈[0,1]
3 for智能体u∈U do
4 ifp<εor ‖Bu‖ 5 随机产生动作au(t) 6 else 7 局部观测,获取状态su(t),将su(t)输入Actor网络θu,产生动作au(t) 8 end if 9 end for 11 将(s(t),a(t),R(t),Rm(t),s′(t+1))存放到经验池B中 12 iftmoddloc==0 13 for 智能体u∈U do 14 从经验重放池B提取大小为d的样本(s(t),a(t),R(t),Rm(t),s′(t+1)) 15 根据式(36)更新本地价值网络参数φ1,u和φ2,u 16 根据式(38)更新本地策略网络参数θu 17 采用软更新方式更新目标网络值 19 end for 20 end if 21 iftmoddglobal==0 22 根据式(37)更新节点全局价值网络参数 23 end if 24 end for 完成训练之后,训练好的模型被直接部署到系统中的用户终端,分布式进行决策。 (39) 仿真在PyCharm平台上完成,仿真参数设置参考文献[10],具体的仿真参数如表1所示。 表1 仿真参数设置Tab.1 Simulation parameter setting 本文选择与其他两种算法进行比较:一种是从不迁移方案(No Migration,NM),任务始终在用户初次卸载的节点上执行,不会随着用户移动进行迁移;另一种是文献[10]所提的基于COMA的任务迁移方案。COMA是一种多智能体强化学习算法,其核心思想是使用集中式评价网络进行集中训练,动作网络分布式学习用户动作决定任务是否迁移。 图3比较了所提算法与文献[10]所提COMA算法的平均奖励值,实线部分为奖励值每50个回合的滑动平均值,阴影填充部分是奖励值变化范围。可以发现,COMA算法在1 000代左右收敛,本文所提DSACM算法在1 500代左右收敛。DSACM算法的收敛没有COMA算法快,但是所获得的累积奖励值高于COMA算法。这是由于DSACM继承了SAC算法最大化熵正则项的思想,鼓励探索,避免陷入局部最优。 图3 算法收敛性分析Fig.3 Algorithm convergence analysis 图4比较了算法在不同学习率下奖励值的变化情况,可以看出增大Actor网络的学习率可以收敛更快,但所获得奖励减小,收敛不稳定。本文将策略网络和价值网络学习率分别设置为0.000 1和0.001。 图4 不同学习率下算法收敛分析Fig.4 Comparison of algorithm convergence analysis with different learning rates 图5(a)对比了在不同用户数量情况任务平均执行时延的变化情况。其中,NM方案的执行时延增长速度最快,这是由于用户任务从不迁移,大量用户聚集在某些服务器上,增加了执行时延。DSACM的平均执行时延小于COMA方案和NM方案,在用户数量增加到一定程度之后,优势更加明显。这是由于所提DSACM方案增加了负载均衡约束,避免了大量任务聚集在某些节点,增加这部分任务执行时延。 (a)平均完成时延 图5(b)对比了不同用户数量情况下的任务失败率。所提DSACM算法的任务失败率始终低于COMA方案和NM方案。用户数量较少时,系统计算资源充足,此时3种方案的任务失败率接近,但随着用户数量的增加,3种方案的任务失败率之间的差距逐渐增大。 图6(a)对比不同移动速度下的用户平均任务失败率,可以看出由于NM算法从不迁移,在用户移动速度较快时,可能产生较大的传输时延从而导致任务失败。DSACM的失败率始终低于其他两种算法,能够在移动过程中保证用户QoS。 (a)失败率 图6(b)比较了不同移动速度下3种算法的迁移率。由于NM选择从不迁移,因此迁移率始终为0。随着用户移动速度加快,为了保障用户QoS,大量任务开始频繁迁移,由于本文所提方案增加了迁移成本控制和负载均衡约束,避免了频繁的迁移,因此迁移率始终低于COMA方案。 图7比较了不同移动速度下系统的平均负载偏差系数。根据前文的定义,偏差系数越小,系统负载分布越均衡。可以看出,不同移动速度对所提方案与COMA方案的负载分布影响较小,且DSACM算法的平均偏差系数最小,节点间的负载分布更为均衡。 图7 不同移动速度下平均负载偏差系数对比Fig.7 Comparison of average load deviation factors for different movement speeds 本文针对MEC中用户移动性导致负载分布不均以及用户QoS下降的问题,提出了一种分布式任务迁移方案,建模了旨在保证用户整体服务质量的优化问题。利用李雅普诺夫优化将问题解耦,并提出一种基于多智能体SAC的分布式迁移算法,采用CTDE框架保证用户可以做出实时性决策。仿真结果表明,相较于现有算法,所提算法能有效降低任务执行时延、任务失败率和迁移率,并能够保证节点间负载分布均衡。3.3 算法复杂度分析

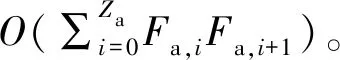
4 仿真结果及分析
4.1 仿真设置

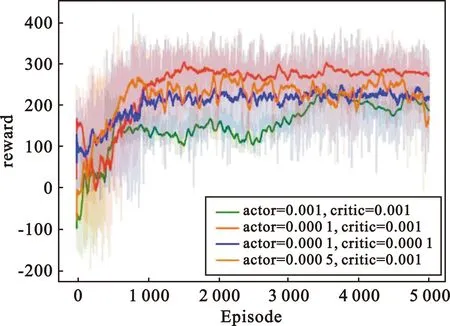
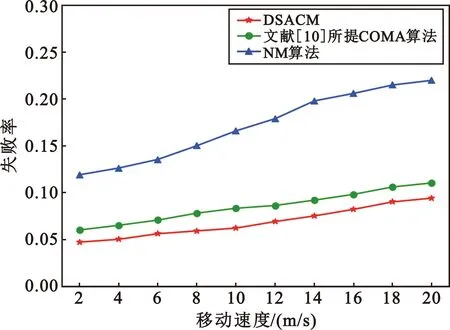
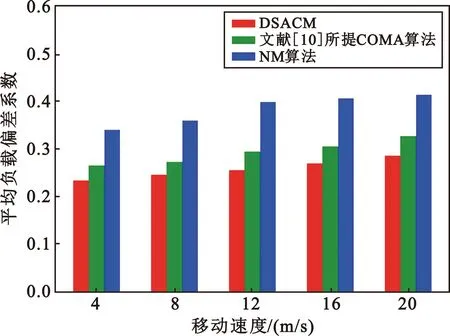
4.2 仿真结果


5 结 论

