平行线中的魔法

文／江苏省太仓市第一中学 陈明子

提到几何，相信大家都不陌生。有时，我们掌握一个几何模型，就可以解决很多与这个模型有关的问题，这也体现了数学的互通性。最近，我做了几道习题，发现平行线中就有这样的魔法。

问题1 如图1，已知AB//CD，求∠A、∠C、∠AEC的数量关系。

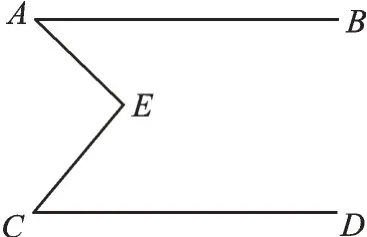
图1

问题2 如图2，已知AB//CD，求∠B、∠BEF、∠EFG、∠DGF、∠D的数 量关系。

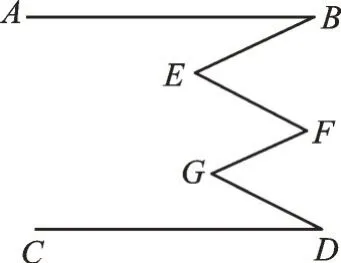
图2

这两道题是有共性的，我都是通过作平行线的方式来解决的。对于问题1，我过点E，作EF//AB，如图3。

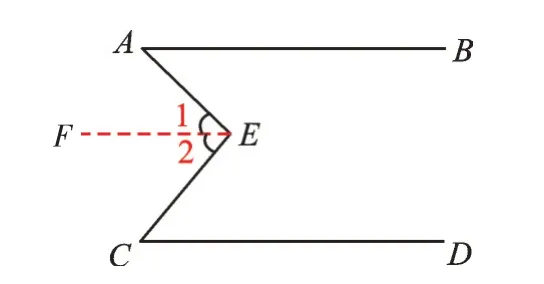
图3

∵AB//CD，

∴AB//CD//EF。

∴∠1=∠A，∠2=∠C。

∴∠AEC=∠1+∠2=∠A+∠C。

对于问题2，我作EH//AB，IF//EH，GJ//CD，如图4。

图4

图5

∵AB//CD，∴EH//GJ。

∴AB//CD//EH//IF//GJ。

∴∠1=∠2，∠3=∠4，∠5=∠6，∠7=∠8。

∵∠BEF=∠3+∠2，∠DGF=∠6+∠7，

又∵∠EFG=∠4+∠5，

∴∠B+∠EFG+∠D=∠BEF+∠DGF。

解了这两道题之后，我不禁产生一个疑问：如果平行线间的拐点继续增多，还能利用作平行线的方法来解决类似的题吗？于是，我思考起下面这个问题。

问题3 已知a//b，求∠Q1，∠Q2，…，∠Qn与∠P1，∠P2，…，∠Pn-1的数量关系（n≥3）。

我又用了作平行线的方法，作了（2n-3）条平行线，还真解决了这道题。

解：如图6，过点P1、Q2、P2、Q3、…、Pn-1，分别作a的平行线，得到l1、h1、l2、h2、…、hn-2、ln-1。

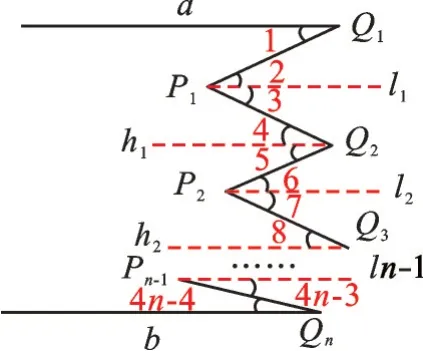
图6

∵a//b，

∴a//l1//h1//…//ln-1//b。

∴∠1=∠2，∠3=∠4，…，∠（4n-3）=∠（4n-4）。

∴∠Q1+∠Q2+…+∠Qn=∠P1+∠P2+…+∠Pn-1。

通过解答这三道几何题，我收获许多，领略到了平行线中的魔法。所以，小伙伴们做数学题时，要学会举一反三，这样可能会有意想不到的收获哦。

教 师 点 评

这是学完“平面图形的认识（二）”后，小作者对“猪蹄”模型的所想所悟。初识几何，小作者能在构建模型的基础上，扩充，探索，领悟，举一反三，获得一般性的结论，培养了数学思维，强化了数学语言，展现了非同一般的数学能力。这也激励同学们，在学习数学的过程中，要学会分析问题，学会从特殊到一般对问题进行更深层次的思考，从而享受学习数学的乐趣。