图形初识 构建知识网——苏科版数学教材七（下）第七章“平面图形的认识（二）”整体解读

文／陶华阳

第七章 平面图形的认识（二）

领 衔 人：朱建良

组稿团队：江苏省太仓市朱建良名师工作室

图形是数学世界中一颗璀璨的明珠。第七章“平面图形的认识（二）”给我们带来什么惊喜呢？下面，让我们一探究竟吧！

一、融贯学习——让知识生长起来

本章开篇，我们迎来了两条直线的一种特殊位置关系——平行。关于“平行”的体验，我们最早是在小学三年级接触平行四边形时得到的。在小学四年级，我们正式接触了“平行”的概念，通过寻找、观察、发现，感受了平行线的特征。如今，七年级所学的同位角、内错角、同旁内角与平行线擦出了新的火花。在本章，我们揭示平行线的基本事实，随后进一步探究平行的条件和性质，为学习几何新知建立基本思路，也为后续图形中平行关系的应用，甚至三角形的相似原理的应用奠定基础。

本章还介绍了最基础的图形运动——平移。小学三年级，我们在方格纸中画平移图形，到小学四年级，沿水平方向或垂直方向画平移图形，获得了初步的图形平移的感受和作图体验。基于此，在本章，我们通过具体实例，探究平移的定义，探索平移的基本性质，进而实现平移的应用。在此过程中，重视运动变化中“变”与“不变”的位置关系和数量关系，能帮助大家初步建立空间观念，培养图形探究的能力，从“运动”的角度进一步加深对平面图形的认识。

三角形作为我们最熟悉的几何图形，在图形的学习中有着举足轻重的地位。在小学，从认识角、边，到基本的分类，我们对它已经有了一定的认识。本章更加突出符号语言的标识和正确表达，是线段和角的学习的延续。三角形中的特殊线段如高、角平分线、中线是本章的重点。认识“三线”的定义，掌握“三线”的作图方法，用符号语言对“三线”的性质和判定进行严谨的表述，能为后续全等三角形和四边形的认识、探究及演绎推理打下扎实的基础。我们还会学习三角形中的内角、外角、内角和、外角和概念，并掌握其中的性质，将其推广到四边形甚至多边形的探究中。

数学的学习往往是利用已有的知识经验去探究新知。回顾本章的旧知基础，比较新、旧知识的异同点，寻找新知识的生长点，自然地把新知识与已有知识科学地联系起来，这是我们数学知识自然生长的过程。

二、整体认知——让思维建构起来

从最简单的几何图形“点”开始，我们认识了“线”，由“线”构造了“角”，继而认识了一些基本的平面图形和几何体，开启了属于我们的“图形之旅”。本章的学习是在认识了线与角的基础上，进一步探究图形位置、图形变换、图形性质及应用。

若想更好地梳理知识，巩固所学，形成知识体系和思维方式，构建本章的思维导图是不错的选择。通过对平行、平移、三角形等核心知识的梳理，我们可以形成一个条理清晰、重点突出、关系严谨的思维导图（如图1）。

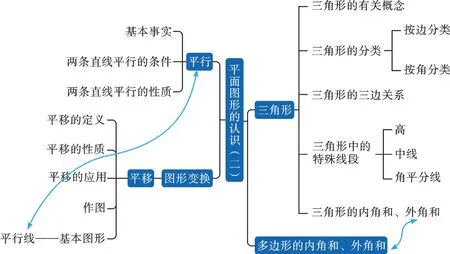
图1

在构建思维导图的过程中，我们要重视对新知的发生过程的体验，通过观察、猜测、发现、论证或计算，对图形的本质属性进行探究。

比如，我们遇到一道题目：

请结合三角形内角、外角及角平分线定理，探究三角形中内角平分线与外角平分线的夹角与顶角的关系。

我们首先用数学语言将其表述出来：已知，如图2，在△ABC中，∠C=80°，AF平分∠BAC，BF平分∠CBE，AF交BC于点D，求∠F的度数。解决之后，我们再对其加以变式，比如∠C=100°呢？∠C=n°呢？你能发现什么规律呢？

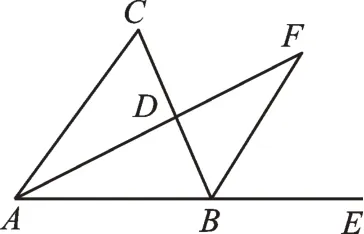
图2

类似的思考和结论可以进一步帮助我们完善思维导图，形成“图像记忆”，使知识间抽象的关系可视化，也便于知识的存储、完善、检索和提取，帮助我们建构符合自己认知的知识结构网。

总之，学习平面图形需要融贯新旧知识，寻找新知学习的切入点，让图形的学习自然发生。注重整体认知结构化的构建，经历观察、猜想、操作、推理、想象等几何学习过程，追求知识本质属性，自然能健全知识结构，提高数学学习能力。