Ultrafast photoemission electron microscopy:A multidimensional probe of nonequilibrium physics
Yanan Dai(戴亚南)
1Department of Physics,Southern University of Science and Technology(SUSTech),Shenzhen 518055,China
2Quantum Science Center of Guangdong-Hong Kong-Macao Greater Bay Area(Guangdong),Shenzhen 518045,China
Keywords: ultrafast photoemission electron microscopy, ultrafast momentum microscopy, excited state physics
1.Introduction
In 1887, Heinrich Hertz made an important observation that the electrical spark between two electrodes could be intensified under ultraviolet light illumination.[1]Such phenomenon, which we now know as the photoelectric effect,has perplexed physicists for nearly two decades until it was explained by Albert Einstein based on his picture of light quantization.[2]Since then, the process of electron emission caused by absorptions of photons, known as photoemission,has played a pivotal role in condensed matter physics research.
Today, the most widely used experimental techniques based on photoelectric effect are angle resolved photoemission electron spectroscopy(ARPES)and photoemission electron microscopy(PEEM).In both cases,one obtains the electronic properties of certain materials in the momentum and real spaces by detecting electrons emitted by the absorption of photons.Of particular interest to studying local electronic properties of matter, PEEM, since the first demonstration of photoelectron imaging by Ernst Br¨uche in 1933,[3]has now evolved to be the prevailing technique for imaging mesoscopic physics.For example, it can spatially resolve electric[4,5]and magnetic[6-9]domains as well as their inhomogeneities, capture the evolution of local electronic nematic order[10]and insulator-to-metal transitions,[11-13]and characterize light induced surface polarization field and spin textures[14,15]with spatial resolution as good as~2 nm in state-of-the-art instrument;[16,17]all of these measurements are essential ingredients to help design materials with quantum properties on demand.[18]
Besides the real space photoelectron imaging,PEEM also allows the integration of angle resolved photoelectron detection,enabling the APRES function based on the same electron optics.[19]Such a combined instrument, which is also termed momentum microscope(MM),allows direct imaging of photoelectron distributions of microscale samples in the momentum space without scanning the sample azimuthal angle.Consequently, PEEM and MM can function as a micron-area APRES instrument,allowing studies of many-body electronic band structures of quantum materials,[20-22]including but not limited to strongly correlated electron systems,[23]topological materials,[24]and van der Waals (vdW) materials[25-29]down to single atomic layer limit.In addition, similar to an ARPES apparatus, a spin filter can also be implemented in MM to study spin polarized electronic structures of magnetic domains.[30,31]Finally, by selectively filtering electrons in certain energy and momentum distributions, MM enables energy- and/or momentum-filtered electron imaging in real space,[32,33]which is analogous to the dark-field optical imaging technique.Therefore, the modern PEEM apparatus combined with MM mode serves as an excellent tool for studying local electronic properties of quantum matter in multidimensions, including energy, spin, real- and momentum-spaces,etc.[34]
Despite the unique capabilities provided by PEEM and MM, most related studies conducted so far, however, are steady state measurements based on a one-photon in, oneelectron-out process.In this linear regime,the photoemission process tackles the many-body electronic wave function approximated by a one-electron removal process,[23,24]which is modified by the interactions among quasiparticles of all sorts, including electrons, phonons and magnons.The contribution to the material electronic properties from each interaction, however, cannot be easily isolated and extracted from the steady state microscopic and spectroscopic measurements, because they modify the time-averaged electron wave functions over the time duration of data-acquisition.More importantly, the detection of coherence effect between quantum states,or quasiparticles,a key to achieving reliable quantum computations,[35,36]is also challenging in steady state measurements.This is because the dynamical information is mostly buried in the spectral width of the desired quantum states, which is affected by a variety of quasiparticle interactions.On the technological side, the energy resolution of PEEM/MM apparatus is also limited by the spectral broadening of the photoelectrons.In the state-of-the-art MM,[37,38]the energy resolution is on the order of a few meV.This intrinsically hinders the direct identification of quasiparticle excitations on the lower energy scale, such as phonon and magnon excitations in the THz to GHz regime that are relevant to acoustic and spintronics[39,40]applications.
Interestingly, these obstacles have largely been overcome by the technological advancements in intense ultrafast laser sources based on the invention of chirped pulse amplification.[41]Following the concept of femto-chemistry developed by Ahmed Zewail,[42]one can adopt two ultrafast laser pulses into a photoemission setup, with one being a strong pump pulse to induce quasiparticle excitations that perturb the electronic ground state, and the other as a weak but temporally synchronized probe to photo-ionize an electron from the pump-perturbed many-body quantum state for spectroscopic or microscopic analysis.By scanning the inter-pulse delay between the pump and probe pulses, the resulted photoelectrons can thus reflect the transients of the corresponding excited state as a function of temporal delay,providing information of the excited quantum state on the time scale ranging from atto-to femto-to nano-second or longer.[21,43-46]
The first demonstration of ultrafast lasers with PEEM was reported by Schmidtet al.,[47]where hot electron dynamics at patterned silver surfaces were spatially mapped with a Ti:sapphire laser, achieving a spatiotemporal resolutions of~20 nm and<100 fs.Soon, it was greatly advanced by Kuboet al.[48]in the imaging of surface plasmon dynamics at structured metal surfaces using interferometrically stable pump-probe pulse pairs.This is a cornerstone experiment of spatiotemporal imaging the phase and amplitude of surface electromagnetic modes, with~10 nm spatial resolution and 667 attosecond(as)time-scanning accuracy;such observation has not been accessible through far field optical imaging or steady state near field scanning techniques.Since then, timeresolved (TR-) PEEM, and particularly interferometric time resolved (ITR-) PEEM have been improved to adapt broadly tunable femtosecond and attosecond light sources,normal incident excitation schemes,full-vectorial imaging method,etc.,making them the prevailing technique in resolving plasmon dynamics.[14,15,48-64]
More importantly, besides their success in imaging of electromagnetic modes,ultrafast PEEM has also been widely applied to imaging the evolutions of magnetic domains and textures in magnetic materials,[65-70]as well as hot carrier and exciton dynamics in metals and semiconductors.[32,71-80]With the implementation of MM, the corresponding studies have been extended to the reciprocal space, allowing multidimensional probing of the corresponding excited states physics.[81-91]Consequently,these investigations thus far have brought substantial improvements in understanding the physical mechanisms of quasiparticle creation,interaction and annihilation dynamics on the nanometer and femtosecond(nanofemto)spatiotemporal scales.
Furthermore, instead of using light as a probe method,one can employ ultrafast light pulses as a control knob to coherently control quantum phases beyond equilibrium on ultrafast time scale.[22,92-95]In strongly correlated systems, ultrafast light irradiation could induce long-lived nonequilibrium metastable states, or hidden states of matter such as transient superconductivity,[96-98]charge orders[99,100]and lattice configurations,[101-103]which are inaccessible from quasistatic stimuli.Generally, light pulses, especially those with high fluence, can even drive new quantum states that do not exist under thermal equilibrium, such as time-periodic Floquet and Volkov states,[104,105]or induce highly nonlinear polarization response in the non-perturbative regime.[106]These aspects of studies, which were mostly carried out in macroscopic systems based on time resolved photoemission techniques, however, have yet to be extensively implemented for microscopic samples in TR-PEEM and TR-MM experiments.With further development of the high power, high repetition rate laser sources, one thus can expect to explore new ways of controlling quantum states of matter and investigate farout-of-equilibrium physics in the strong-field regime on the ultrasmall and ultrafast spatiotemporal scales.Therefore, not only can TR-PEEM/MM studies improve the understanding of quantum excitation pathways in solids,it may also lead to new theories and possibilities in generating new phases of matter beyond thermal equilibrium.[22,92,93,95]
Regarding the studies of excited state physics in condensed matter,it is thus of particular interest to review the relevant fields of research advanced by ultrafast PEEM and MM.We note that reviews of TR-PEEM and TR-MM with specific research topics, such as plasmonics and transition metal layered materials,have been reported.[43-46]Here,in this review,we intend to give an in-depth overview of the TR-PEEM/MM research, including technical developments of the instrument and light sources, and applications in several different condensed matter research fields.We first introduce the basic concept of PEEM and the mechanisms of its imaging contrast,as well as some technical aspects of the apparatus and the ultrafast light sources used in TR-PEEM experiments.Next,we briefly report the TR-PEEM/MM applications in studying physics that are out-of-equilibrium,including spatiotemporal,energy and momentum evolutions of surface plasmons, hot electrons,electron orbitals,excitons,and spins.We emphasize that this review is aimed to cover the research possibilities enabled by ultrafast PEEM/MM technique,and thus the subjects and references included here are far from complete.We refer interested readers to the review articles of specific subjects for detailed information of the corresponding research field.We close this review by discussing the potential applications of(I)TR-PEEM and TR-MM in studying nonequilibrium physics in condensed matter systems beyond metals and semiconductors,as well as important questions that may be addressed by these techniques.
2.Photoemission electron microscopy
As a photoemission-based apparatus, PEEM is a surface sensitive technique that is designed to spatially measure the electronic properties of materials of interest.Therefore, it is important to understand the types of contrast that can be imaged by PEEM,and how different designs of PEEM electron optics and illumination light sources can influence the experimental measurements.In this section, we first present a few main contrast mechanisms in forming PEEM images, including work function,band structure,magnetization,and nonlinear photoemission contrast.We then review the designs of commonly used PEEM and MM,discuss their difference in the electron optics,advantages and disadvantages in data acquisition.Finally, we briefly overview the types of ultrafast laser sources that have been implemented into PEEM and MM,such as broadly tunable femtosecond ultraviolet(UV)-visible-near infrared(NIR) pulses from laser oscillators or amplifiers, extreme ultraviolet (EUV) pulses generated by gas-phase high harmonic generation(HHG),and sources that can potentially be employed to extend the studies of nonequilibrium physics in a broader wavelength regimes.
2.1.Imaging contrast
Figure 1 schematically shows the basic working principle of a PEEM apparatus.The sample is usually placed a few mm in front of the PEEM electron objective lens.Excitation light sources can be introduced onto the sample from the surface normal,a large oblique angle,or its back side.The photoelectrons produced by light illumination,which intrinsically carry the information of the underlying quantum states, are accelerated by the PEEM objective lens for further magnification and imaging.In solids,the one-electron wave function is usually affected by a variety of interactions, including electronelectron,electron-phonon,electron-magnon,etc.In addition,excitations of surface electromagnetic modes,such as surface plasmons(SPs),can also influence the spatial distributions of surface electrons.Therefore,by photo-ionizing these electrons via one or multiphoton absorption processes, one can image the local electronic responses in real (PEEM) and reciprocal(MM)spaces using the proper electron imaging mode,reflecting the underlying many-body physics.These processes,however,may cause different PEEM contrasts,as will be discussed in detail below.
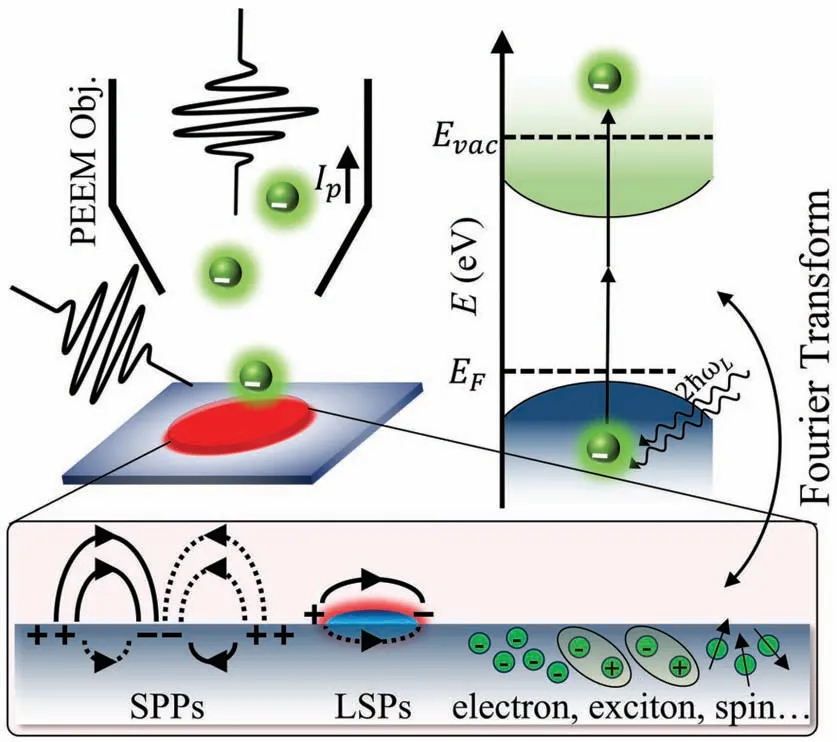
Fig.1.Schematic of the working principle of PEEM imaging.The sample is placed in vacuum, a few milimeters away from the PEEM objective lens(Obj.), between which a high voltage of ~10-20 kV is applied.When light illuminates the sample either from the surface normal or at the grazing incidence angle,electrons can be ionized from the surface.Subsequently,photoelectrons are accelerated and collected by the PEEM objective lens for magnification and imaging.The resulted PEEM images reflect plenty of physical phenomena, including surface plasmon polaritons (SPPs), localized surface plasmons(LSPs),and other intrinsic quasiparticles.When two or more light pulses are employed, it allows the implementation of the temporal-resolving scheme, such that the first pulse stimulates the ground state, and the subsequent pulses interrogate the corresponding excited state physics for PEEM analysis.Besides real space PEEM imaging, Fourier transforming the real space photoelectrons into reciprocal space offers the information of the material electronic band structures as a function of energy and electron quasimomenta.
2.1.1.Work function
Early investigations of photoelectric yield were carried out by Fowler and DuBridge,[107,108]with a focus on explaining the temperature and wavelength dependent photocurrent,and the non-abrupt onset of photoelectric current above the threshold frequency.Based on extensive experimental results in several metallic systems,such as silver,gold,tin,etc.,they have proposed an analytical model for the current density approximated to the leading order,whereTis the sample temperature,Φis the work function (WF),hνis the photon energy, andkBis the Boltzman constant.In the perturbative regime, the Fowler-DuBridge (F-D) model accounts well for the smooth photoemission intensity,especially near the work function edge.In addition,besides modeling the photoelectric effect from a statistical mechanics point of view,the photoelectron current in both linear and nonlinear regimes can also be derived quantum mechanically from the simplest free-electron gas model,[109]where one considers a weak and constant vector potentialAfor plane wave excitation(A2~0 and ∇·A=0), and a sharp surface termination potential.In this case, the solution to the dipolar interaction Hamiltonian∇results in partial photoelectron current densityJn,withnbeing the nonlinear photonic order for the photoemission process.Whenn=1, it resembles the F-D photoemission model.While the detailed modeling is beyond the scope of this review,we note thatJnis proportional to the 2nthpower of the surface normal electric fieldE⊥,which is manifested in several multiphoton photoemission experiments such as the plasmonic photoemission discussed in Section 3.We note that contribution to photoemission signals fromA2̸=0 term was also discussed in plasmon-assisted emission.[110]
Based on the F-D model, when the excitation light is monochromatic of certain energy, the photoelectric current density, and thus the photoemission intensity increases quadratically with decreasing WF.Therefore,it makes PEEM a sensitive tool to characterize surface WF.This is particularly useful because the local WF of the samples of interest is usually inhomogeneous, and varies across regions or domains of different crystal orientations,[111-113]ferroelectric polarizations,[5]elemental compositions,[114,115]etc.In addition, despite that the F-D theory is formulated based on free-electron models, it also shows excellent prediction accuracy for photoemission intensity in semiconductors and insulators,[116]which makes PEEM an excellent tool for the qualitative understanding of sample WF.There are, however,several limitations in the F-D theory,as it does not include any band structure and spin information,which offer other contrast mechanisms in PEEM imaging.
2.1.2.Band structure
The PEEM contrast due to WF difference discussed above is a special case of the band structure effect.In conventional ARPES experiments, the momentum space photoelectron spectra measure the one-particle spectral function of the corresponding band structure.Therefore, by projecting energy and momentum filtered electrons onto real space for photoelectron imaging, PEEM can produce dark-field images with the contrast given by the filtered electronic band structure.Such capabilities have been reported by Maklaret al.in imaging charge density wave materials,[33]and by Schmittet al.in visualizing excitons in layered transition metal dichalcogenides.[32]Another potential observable in the electronic band structures that may be resolved in PEEM experiments is the surface state at material surfaces or interfaces.[117,118]These surface states are usually sensitive to light polarization and photon energy, which could provide stronger photoemission signal than that of bulk states in specific excitation configurations.
Despite having such a possibility,the effect of band structures on PEEM experiments has yet to be explored extensively.The challenge lies in producing high-repetition rate and high photon energy light pulses that allow efficient detection of high momentum electrons.This is partly resolved by MHz rate EUV light based on gas-phase HHG processes, as will be introduced in Subsection 2.2.3.
2.1.3.Magnetic contrast
The magnetic contrast in PEEM experiments is closely related to the materials electronic band structures.Kramer’s degeneracy requires the electronic states to be doubly degenerate at high symmetry momenta under time-reversal symmetric condition.In the presence of electron spin-orbit coupling,electron correlation, or (effective) magnetic field, such symmetry is lifted,giving rise to spin-split bands within the entire Brillouin zone.Because of the dipole selection rules, such spin-split band can usually be distinguished as two separate peaks in the photoemission spectra under circularly polarized light (CPL) illumination, which is termed as circular dichroism effect,[119]described by CD=(Ileft-Iright)/(Ileft+Iright),whereIleft(right)labels the photoemission intensity under left(right) CPL.[120,121]In real space, when permanent magnetization is present, such as magnetic domains, the left and right CPL propagating along the magnetization direction will also interact differently with the materials of interest, giving rise to magnetic CD, or MCD, signals visible to PEEM imaging.[122-124]We note that not only electron spins or macroscopic magnetization domains can induce CD effect,electronic or structural chirality in non-magnetic systems,such as in biomolecules,can also result in significant absorption of light of opposite helicities.In addition, contrast due to linear dichroism LD=(Ip-Is)/(Ip+Is),whereIp(s)represents the intensity of p(s)polarized light,can also be imaged by PEEM.Such effect is rooted in the imbalanced spin population by magnetic anisotropy,and thus is subjected to more symmetry requirement.[124,125]
In MCD or magnetic LD(MLD)experiments, the probe light is usually from synchrotron-based light sources,such as high flux soft x-rays.In this case,because of the high photon energy,spin-dependent core level electrons can be photoemitted and imaged by PEEM,allowing element specific magnetic contrast.Finally,it should also be noted that MCD effect can also be induced with nonlinear multiphoton photoemission using visible light.Specifically, when femtosecond low energy photons are employed,multiphoton processes can produce far more imbalanced spin distribution, if 1) proper intermediate state is present, and 2)resonant absorption condition is satisfied.Therefore, the excited states CD effect can be observed on the ultrafast time scale.[126]
Today, the x-ray MCD and MLD PEEM are widely employed in the magnetism community.There exists a large body of related research on both steady state and excited state physics, and the brief overview presented above is far from complete.In Section 3, we will introduce a few examples of imaging magnetic materials in the time domain and leave steady state experiments not discussed.
2.1.4.Nonlinear photoemission contrast
Two-or multi-photon photoemission based on femtosecond laser pulses opens a new door for producing photoelectron contrast in both real and momentum spaces.This is because the photocurrent produced by nonlinear photon absorption scales with the 2nthpower of the photonic ordern(Subsection 2.1.1),so that stronger photoemission yield is expected with higher field strength.This is particularly true for fields that have large surface normal components, such as surface plasmon fields at metal surfaces.When the light or surface plasmon fields are spatially modulated on materials surfaces,the photoemission intensity distribution is thus determined by the local field intensity in a non-linear manner,[44,45]which eventually allows the imaging of polaritons in space and time using photoelectrons on the nano-femto scales.
Beyond the F-D and free electron gas models,Keldysh[127]proposed a dimensionless parameter,γ=whereUpis the ponderomotive energy of an electron, to distinguish different intensity-dependent light-matter coupling regimes.[128]Forγ ≫1, the system is at weak coupling regime, such that the distortion of electron potential is negligible, and the photoemission process resembles that of the classical model described above.Whenγ ≪1,the perturbative picture is collapsed,and the electron emission enters a strong coupling regime, such that electron tunneling between atomic core and vacuum naturally occurs due to the strongly bent potential surface.In this case, electrons can be produced and accelerated with great efficiency in the strong electric field,such as localized plasmon field at its resonance,but it also creates a broader energy distribution that degrades the spatial and energy resolution of the PEEM instrument.[129,130]
Finally, besides synchronized monochromatic multiphoton photoemission,the nonlinear photoexcitation pathways in solids further allow a temporal contrast based on the pumpprobe technique.Specifically,two pulses having a mutual delay Δtcan be considered as a pump and probe pulse pair.The first light pulse (pump) can excite an electronic transition or induce a surface polarization such that the system is in its excited state.[21,93]Subsequently, a second probe pulse comes and ionizes an electron for PEEM imaging.Because the quantum state prepared by the pump has a finite decoherence time and population lifetime, the probe pulse can thus detect the evolution dynamics of the excited states by delayed photoionization.We note that the pump-probe temporal contrast is only an extension of the nonlinear optical effect,and basically reflects transient changes in the physical properties discussed above,such as WF or band structure of the materials under investigation.Therefore, the pump-probe method, and two- or multi-photon absorptions are the building blocks for studying condensed matter physics beyond thermal equilibrium.
2.2.Technical overview
2.2.1.PEEM apparatus
There are two main categories of PEEM apparatus being broadly used in independent research groups and large research facilities.The difference is that one is based on the electrostatic-lens system for photoelectron collection and imaging, and the other is based on magnetic electron lenses.[131]
The design of the electrostatic PEEM follows that of the prototype of photoelectron imaging system developed by Br¨uche,[3]which consists of an electrostatic electron objective lens, a straight column for electron propagation, projection and magnification, and a detecting fluorescent screen[Fig.2(a)].The spatial resolution of such design is~10 nm theoretically,which is determined byδ~E/(eF),[132]whereEis the emission energy,eis the electron charge,andFis the electric field strength between the sample and the objective lens; additional factors, such as the spherical and chromatic aberrations of the lens, energy spread of the photoelectrons,must also be considered.[133,134]In practice, a spatial resolution of<50 nm can be conveniently achieved under continuous wave(cw)excitation.In addition,due to the linear propagation geometry, the imaging column can also be upgraded with an electron drift tube,electron energy filters and a delayline detector to allow time-of-flight(ToF)detection,such that the flight time of photoelectrons from the sample to the detector is correlated with the electron energy.[135-138]Therefore,it offers the capability of energy resolved PEEM imaging with a resolution of~100 meV, or capturing the electron dynamics with picosecond resolutions.Furthermore, it also enables the integration of MM functionality simply by projecting the real space photoelectrons to the reciprocal space for momentum resolution.Such PEEM apparatus is commercially available at Scienta GmbH and Specs GmbH.

Fig.2.Designs of four widely used PEEM apparatus.(a)Electrostatic lens based PEEM with a straight electron column and ToF detector.(b)Magnetic lens based PEEM including a HA and an electron gun.The electron gun usually produces continuous wave electrons that impinge and reflect from the sample for LEEM imaging.The two 60° beam splitters are designed for directing electron beams for the LEEM mode,and the subsequent aberration correction(AC)based on the electrostatic AC mirror set,respectively.The HA offers the energy resolution of the imaging electrons.(c)Magnetic lens based PEEM with two 90° magnetic prism arrays and an electron gun.The prism arrays are electron beam splitters that allow LEEM imaging and aberration correction.(d)PEEM with double HAs.The analyzers are arranged such that the aberration produced from each analyzer gets canceled by symmetry.Such configuration is typically optimized for reciprocal space imaging,i.e.,for momentum microscope.In all cases,the real and momentum space planes of the electron optics are labeled.The illumination paths are also indicated by numbers and the red rays.
In terms of the optical excitation configurations, three schemes are commonly implemented,as indicated in Fig.2(a)by the red rays.The oblique excitation 1○was adopted for most early PEEM experiments because of the ease of operation.[48-51,53,54,139-151]In this case,the laser pulse is usually incident at an angle of 65°from the surface normal.When the light field is TM-polarized, that is, with the electric field polarization lying in the plane of incidence, it provides a large surface normal electric field for the sensitive detection of surface polarizations,such as plasmonic responses,[152]and the image potential states on metal surfaces.[153,154]The TEpolarization is that the electric field is polarized perpendicular to the incidence plane.Such TM-TE convention is consistently used throughout the text for grazing incidence condition.For normal-incidence excitation,we describe the polarization to be horizontal and vertical with respect to the horizontal axis of the image.Another excitation scheme is for light illuminating from the surface normal,which is more challenging because it requires directing the laser beam through the electron imaging column and the objective lens.This is achieved by inserting into the electron imaging column a non-magnetic mirror [dark grey element in Fig.2(a)] that can deflect the light pulses to the sample.[155]Note that the illumination angle is not precisely along the surface normal, but slightly tilted by~4°,such that the mirror does not prevent the para-axial photoelectron propagation.More recently, illumination from the rear side 3○has also been achieved either by inserting a mirror that can reflect the grazing incidence light normally onto the back side of the sample,[56,156]or inserting a lens that allows focusing of the light incident from the back side of the chamber to the sample.[57]Such scheme requires the sample substrate to be transparent for light to pass through.
Besides the advantages discussed above, there are still certain limitations to the electrostatic PEEM.First, the ultimate spatial resolution is limited by spherical aberrations of the electron optics and the chromatic aberrations of the imaging electrons, which cannot be easily compensated in the linear electron-optics geometry.[131]Second, the ToF detection requires pulsed excitation,preventing convenient characterizations using mercury(Hg)discharge lamp.This puts further requirement on laser repetition rate for efficient data acquisition;an upper limit of the laser repetition rate is also set by the ToF counter as~4 MHz in most commercial instruments; exceptions also exist where light of repetition rate up to~500 MHz can be used.[157]Finally,the straight propagation column cannot be combined with an electron gun to perform low energy electron microscopy(LEEM)and low energy electron diffraction (LEED) for the characterization of sample tomography and crystallinity, as can otherwise be achieved in PEEM system having magnetic deflectors[Figs.2(b)and 2(c)].
In magnetic-lens based PEEM setups, photoelectrons are first collected by a magnetic triode or tetrode objective lens,[158,159]and subsequently deflected by a set of magnetic sector field or magnetic prism arrays during the projection and amplification processes, before finally reaching the fluorescent screen for PEEM imaging.Figures 2(b) and 2(c) show the schematics of the LEEM-PEEM from Elmitec GmbH,and AC-PEEM-90 from Specs GmbH, respectively.The excitation beam paths are also included as red rays.The advantage of having electron deflectors is that the deflection geometry allows one to implement additional components into the vacuum chamber, such as an electron gun (e-gun) for LEEM and LEED studies, or a set of electrostatic mirrors to compensate the spherical aberrations of the photoelectrons introduced by the electron lenses.Interestingly, the aberration introduced by the magnetic deflector can also be compensated by adding a second, identical deflector arranged in an antisymmetrical configuration as shown in Figs.2(b) and 2(c).Therefore,it greatly enhances the spatial resolution of LEEMPEEM,which reaches~2 nm in the cw excitation limit.[16,17]
The spectroscopic imaging of photoelectrons in magnetic lens based PEEM can be achieved in a similar way for conventional ARPES instrument.For Elmitec PEEM, the electrons are sent through an additional hemispherical analyzer(HA)for energy resolution,which can reach~50 meV in the state-ofthe-art design;[160]in the case of Specs PEEM,it is achieved by the dispersive magnetic prisms, which offers a resolution of>200 meV.[161,162]We note that the ultimate energy resolution is limited by the Heisenberg’s space-momentum uncertainty principle: because the design of PEEM electron optics is aimed to achieve superior spatial resolution, the large acceptance angle in the reciprocal space in turn degrades the momentum and energy resolutions.In addition, the acquisition methods also vary in these two instruments.In Elmitec PEEM, a single imaging captures a constant energy map of photoelectrons in the momentum space.It thus requires a series scans of the photoelectron energies to obtain a complete electronic band structure.In the Specs AC-PEEM-90 setup,however,an energy slit is introduced in the momentum space,effectively projecting a slice of electron energy vs.parallel momentum onto the imaging detector.In this case,instead of scanning the energy axis, one needs to scan the slit position along the desired momentum directions to obtain the full band structure.We note that such scanning is much less efficient than that of the ToF detection when full-Brillouin zone information needs to be obtained.
2.2.2.MM apparatus
An exciting extension of PEEM is the projection of its real space photoelectron distribution to the reciprocal space for photoelectron diffraction imaging, i.e., angle resolved photoelectron imaging.Such switching between real and momentum space imaging can be conveniently achieved through setting up the voltages applied on a set of electron lenses.In this case, the PEEM transforms into a so-called momentum microscope,enabling energy and angle(momentum)resolved photoelectron spectra over micron sized samples.This is different than the conventional micro- or nano-ARPES, where one is required to reduce the illumination beam size and scan over the region of interest to obtain a real space band structure mapping.Instead, MM captures the momentum space images using photoelectrons coming from a micro-sized region that can be defined by the mechanical apertures being used.For this reason,the spatial resolution of the MM is limited by the smallest aperture one can use.The advantage of MM, however, is that one can directly filter electrons from a certain energy and momentum, and perform corresponding PEEM imaging.In this configuration,the spatial resolution is limited by diffraction limit of the photoelectrons,which is typically on the order of a few nm and much better than that of the raster scanning type micro-APRES.Regarding the acquisition method,in the case of ToF-PEEM,the dataset obtained in one acquisition contains both energy and momentum space information.Here,the parallel momentum is achieved via direct 2-dimensional(2D)imaging,and the energy axis is obtained via ToF.Therefore, a single acquisition can reveal the electronic band structures in the full surface Brillouin zone.
Next, we extend the discussion to a new design that is aimed to improve the energy resolution of the MM.Figure 2(d)shows the schematic of a commercially available MM(Nano-ESCA) from Scienta GmbH,[38,163]along with its excitation scheme.It consists of a PEEM objective lens and a pair of HAs.In this case, photoelectrons from micron-sized region are collected by the PEEM objective lens, and subsequently sent through two identical HAs for energy resolution.The design of the identical HA pair removes the spherical aberration by symmetry, similar to the designs in Figs.2(b) and 2(c).Consequently,it yields~10 meV energy resolution and 40 nm spatial resolution with VUV light excitation,but comes at relatively high cost.[38]
Another MM instrument based on single HA has also been developed by Specs GmbH,i.e.,the Kreios MM.In this design,the objective lens is slightly farther away from the sample,degrading the spatial resolution of the PEEM mode to be~100 nm.This, however, effectively improves the energy resolution, which could reach~5 meV.A third option is to append a ToF drifting tube after the first HA, which can circumvent the nonlinear aberrations introduced by the first HA and achieve energy resolution of~7.7 meV;[37]this design,however, is not commercially available yet.Finally, we note that one can in principle append an electron spin filter in the electron optics,but it is not broadly investigated so far.
The unique feature of MM is that it captures electrons emitted at all angles(±90°)for spectroscopic analysis,which allows the acquisition of photoelectrons having higher parallel momenta without tilting the sample azimuth.When EUV light sources are employed, the MM can therefore efficiently detect electronic structures in the entire Brillouin zone in one shot.This is in contrast with conventional ARPES experiment,where the collection angle is within~±15°,and sample tilting is required to image photoelectrons at high emission angles.Obtaining the full Brillouin zone information thus requires collaging the measurements at each angle,setting up another challenge in quantitative analysis of the electronic band structure.The large momentum accessibility enabled by MM,however, is at the expense of the angular and energy resolution, because electrons having higher momenta are squeezed into a paraxial photoelectron beam for imaging.This further causes significant space-charge effect because a large number of electrons can interact with each other due to the Coulomb force along their way to the detector;[141,164]work is also being done to minimize the space-charge effect.[165]
Finally,as described above,the Heisenberg’s uncertainty relation limits the superior spatial and energy resolutions simultaneously.While PEEM is aimed to achieve higher spatial resolution, MM is usually designed to reach high energy resolution in exchange of spatial resolution.The state-of-the-art energy and momentum resolutions are around<5 meV and 0.008 °A-1, respectively.While not reaching the resolution limit of conventional ARPES,the uniqueness of having an objective lens is that one can perform MM imaging in a micronsized area, i.e., micro-ARPES, without raster scanning.This opens the door to study the influence of surface inhomogeneity on electronic structures, as well as monolayer vdW materials that are typically a few microns in size.
2.2.3.Ultrafast light sources
Conventional light sources for PEEM and MM studies are mostly light produced by mercury and helium discharge,with photon energies of 4.9 eV and 21.2 eV.These are unpolarized cw sources that can be used for steady state work function imaging and band structure mapping.In this section,we go beyond cw sources, and focus on discussing ultrafast laser pulses that can drive two- or multi-photon photoemission for TR-PEEM/MM imaging.We overview femtosecond light sources from near infrared to EUV regime and discuss the difference in the physics problems one can address with these light sources.
2.2.3.1.Laser oscillators
The most common excitation sources for TR-PEEM experiments are generated from the commercially available Tisapphire oscillator,with wavelength of~800 nm,photon energy of 1.55 eV, repetition rate of 70-100 MHz, pulse duration of 10-100 fs, and pulse energy of a few nJ.In principle,ytterbium-doped(Yb-doped)fiber oscillator of energy 1.24 eV can also be employed, but its application is rare because the typical~300 fs pulse duration is too long for resolving electronic excitations.Therefore,the following discussion is only for Ti:sapphire oscillators.
Because the WF of typical materials is~4-6 eV, a common excitation source for one-photon PEEM imaging is the 4thharmonic of the fundamental pulse, which is usually~200 nm,or~6.2 eV.This provides an excellent method to characterize the WF inhomogeneities in most materials, but no dynamical information is obtained.In case of photoexcitation using the fundamental laser, as is usually employed for monochromatic two-photon photoemission (2PP) experiments, the two-photon energy (~3.1 eV) is too low to overcome the materials’WF.Consequently,a WF reduction treatment is required.For example,by chemisorption of Cs atoms,the WF can be reduced so that two-photon energy quanta are sufficient for electron ionization.This typically applies to the imaging of plasmons in metal systems, where the local Cs atoms reduce the WF but their modification to the plasmonic response is negligible.[55,155,166]In the case of using second harmonic(SH)of the Ti:sapphire laser as light source,the two photon energy quanta (6.2 eV) can easily overcome the WF of most materials, but it should be noted that the excited unoccupied states and their relaxation dynamics would be different than those excited by the fundamental harmonic.[48,49,60]Finally, one could also induce photoemission through higher order processes, such as 3-photon and 4-photon excitations,but such processes usually have low transition probabilities,and require much stronger excitation light intensity with much shorter pulse duration.[62,167]
In dual-color experiments, such as for spatiotemporal imaging of hot carriers in semiconductors, the wavelength of the pump pulses is usually 800 nm or 400 nm, as long as it is sufficient to induce above band-gap transitions; the probe pulse,however,is usually the third and fourth harmonics(4.65 eV or 6.2 eV)of the fundamental beam, which provide sufficient photon energy to ionize electrons from the unoccupied states, and increase the detectable electron momentum range.[60,76,77,168,169]The upper limit of the probe photon energy produced by direct 4thharmonic generation is limited to~6.1 eV.This is because 1) the pulse energy is limited to support efficient harmonic generation of higher energy photons, and 2) there is no accessible phase matching condition;extension of photon energy to~6.2 eV can be achieved by producing the 4thharmonic via mixing the fundamental and 3rdharmonics.[170]To achieve detection of photoelectrons in higher momentum, photon energy of>20 eV is required,which can be obtained from high harmonic generation(HHG)processes pumped by strong laser pulses of~100µJ to several mJ,as will be discussed below.
2.2.3.2.Tunable light sources by parametric amplifiers
In general, to characterize unoccupied electronic states,light sources of variable photon energies are also strongly needed, particularly when studying interactions between two electronic states where resonance transitions or couplings are critical.Such upgrade is accomplished by the sophistication of the chirped pulse amplifiers,[41]as well as the colinear and non-colinear optical parametric amplifications (OPA and NOPA).[171]The former provides high pulse energy (µJ to mJ), high repetition rate (kHz to MHz) laser pulses, with pulse width ranging from a few to~300 fs, which serve as an excellent pump source for parametric amplification;the latter provides broadly tunable fs light pulses.In OPAs,a highpower femtosecond pump pulse,usually from a laser amplifier,and a weaker supercontinuum seed pulse, typically produced by nonlinear filamentation in dielectrics, are overlapped in a nonlinear crystal, such asβ-barium borate (BBO), where the mixing between the two pulses causes parametric conversion and amplification.Because of the broad spectrum of the supercontinuum seed light,the pump pulse can selectively amplify a certain spectral region within the supercontinuum according to their phase-matching condition,thus providing a broad tunability of the amplified pulse.The generated pulses typically have a pulse duration on the order of those of pump and probe pulses in a colinear geometry, but can be significantly shortened to a few cycles in a noncolinear geometry due to the more restricted phase-matching criterion.[172]The output light can be further extended to a broader spectral range by frequency doubling,sum frequency generations,difference frequency generations, etc., enabling PEEM measurements from deep UV through visible to IR,and even THz regime.For example,beyond excitation in the visible regime,light in the telecommunication wavelengths (1550 nm) has been employed for multi-photon photoemission for the study of plasmonic responses in silver nanoparticles.[173]This offers new ways of looking at plasmonic responses with strong field excitation,possibly in the regime that is beyond the perturbative description.Therefore, using the output from OPA and NOPA as a pump source for ultrafast PEEM experiments,one can expect the exploration of a broad range of excited state physics,ranging from low energy excitations such as magnons and phonons in topological materials and superconductors,to high energy excitations such as plasmons,excitons,and other light-matter hybrid modes in metals and semiconductors.[22,92]
In terms of the probe pulses, the common scheme is to employ a UV or deep UV light that can be obtained by parametric conversion from the visible output of OPAs or NOPAs.This is, however, similar to that of the harmonics of the Ti:sapphire oscillator,with an upper limit of about 6.2 eV due to the phase matching condition for frequency mixing and the band gap of BBO crystals.[170]Therefore, with the desire of imaging electrons from broader unoccupied states both in PEEM and ARPES studies, significant research effort has been carried out in developing table-top EUV[174-184]and xrays sources.[185,186]In the case of EUV pulse generation, it typically requires focusing of high energy (>100 µJ) ultrashort pulses (<50 fs) into an inert-gas filled fiber capillary or gas jet, where extreme nonlinear processes, such as high harmonic generations, occur due to the strong electric field of the pump pulse.Such process can be described by a conventional three step model beyond perturbative regime,[187]which will not be discussed here.With 800 nm light as a pump, the resulted photons usually have odd harmonics between the 21stand the 33rd, with photon energies between~32.5 eV and 51.1 eV.[174-176,178,179,181]When the pump light is the second harmonic of the Ti:sapphire laser output,it typically produces the 7thharmonic, corresponding to an energy of~22 eV.[177,180]In case of the Yb-doped amplifiers, both the fundamental (~1030 nm) and its SHG (~515 nm) can serve as the pump for the HHG, which produces EUV photons with optimal energies around the 21th(25.2 eV),and the 11st(26.5 eV)harmonics,respectively.[182-184,188]Using such EUV photons as probes,one can conveniently access electrons in the entire Brillouin zone for real and reciprocal space imaging.Note that light at other photon energies can also be produced via different harmonic generation processes,[189,190]but their application is yet to be explored extensively.
We note that typical ultrafast EUV sources have pulse duration comparable to that of their pump light.The resulted EUV photons, however, are produced only within a fraction of an optical cycle, i.e., hundreds of attosecond, through the electron tunnelling and recolliding processes.Therefore,EUV light pulses are effective trains of attosecond pulses of EUV photons.[191-193]In fact,the efficiency of such process is very sensitive to the carrier envelope phase (CEP) of the pump pulse, especially when the pulse duration is only a few cycles.This is a critical factor that needs to be considered if one intends to obtain precisely synchronized attosecond pulses for resolving sub-femtosecond electron dynamics.In this case, a CEP locked laser amplifier is usually recommended, but is at a relatively high cost.
While ultrafast EUV probes, and in general attosecond probes,have been applied to TR-ARPES and TR-MM experiments for over a decade,their application to real space PEEM imaging is still in its infancy.[32,50,194,195]This is mostly hindered by the low repetition rate(1-10 kHz)of the laser sources employed so far.Even with 10 kHz repetition rate, imaging photoelectrons in real space still requires extremely long acquisition time (hours) to obtain a single image.This puts a challenge in maintaining the spatial drift in the sample and PEEM alignment.Nevertheless,the EUV-based PEEM imaging will certainly experience fast development with the advancements of high-repetition rate lasers.Finally, we note that the development of bright and tunable free electron light sources is also of benefit to PEEM studies,[89,196]for it enables the detection of the local electronic structures along all momentum axes.
2.2.3.3.Interferometric pulse pairs
Finally, we discuss a special excitation scheme for TRPEEM experiments, which employs a pair of colinear, and identical fs pulses from IR to UV regime.[44,45,197]The pulse pair is usually generated by a Mach-Zehnder interferometer(MZI).In this case, one arm of the MZI is scanned with attosecond accuracy relative to the other arm,forming an interferogram as the excitation light, similar to the pump-pump pulse pair in two-dimensional electron spectroscopy.[198]Therefore, this excitation configuration can provide subfemtosecond amplitude and phase information of the quantum states of electrons or electromagnetic modes.By performing Fourier analysis along the scanning time axis,the harmonic information of the nonlinear photoemission process can be extracted, enabling the studies of different quantum pathways contributing to the photoemission process, as well as the coherence between different quantum states.Details of such excitation scheme can be found in the excellent review by Petek and Ogawa.[197]So far, the interferometric time resolved PEEM (ITR-PEEM) has been aimed to perform vectorial imaging of plasmonic field dynamics with nano-femto resolutions,as will be discussed in detail below.We note that the time resolution in ITR-PEEM experiment is still limited by the two-pulse correlation,which should not be confused with the attosecond scanning accuracy,i.e.,phase resolution.
By treating the pulse pair as an interferometric pump source, and introducing a third pulse for photoionizing the photoelectrons,one is allowed to perform Fourier analysis on both the pump-pump pulse delay, as well as on the pumpprobe pulse delay.This excitation scheme adapts from the well-known 2D electron spectroscopy (2DES) setup,[199-201]which offers information on the dynamics as a function of excitation and detection frequencies, such that the coherence among quantum states can be revealed.More specifically, in 2DES, by Fourier transforming the pump-pump delay, one obtains the excitation energy; besides, at each time delay,the quantum states prepared by the pump pulse pairs can be probed by the third pulse using a spectrometer, which provides the probe energy resolution.Therefore, one essentially acquires 2D maps with horizontal and vertical axes representing the excitation and probe energies at a specific pump-probe delay time.Such 2D spectrum thus contains the information of coherence among the quantum states being probed.By delaying the pump-pump pulse pair and the probe pulse, it is therefore expected to produce a sequence of such 2D spectrum that can reveal the dynamics of the quantum coherence.We note that variations of the pulse excitation scheme,such as introducing a local oscillator to perform 4-pulse illumination,can also be implemented.In case of a PEEM experiment,one could also employ a three-pulse illumination scheme of pumppump-probe type, and acquire photoelectrons in real space.Here,the Fourier transformation on the two delays provide the excitation and detection frequency information.Therefore, it offers the coherence information with nanometer spatial resolution, which terms such setup as a 2D nanoscopy, as will be shown later in Subsection 3.1.3.
3.Real space imaging
3.1.Localized surface plasmons
Light can be coupled with ultrafast surface plasma oscillations at subwavelength metallic particles to form localized surface plasmon(LSP)quasiparticles.[152]They are subwavelength electromagnetic modes,which are featured to have strong field enhancement and confinement, especially at the LSP resonance energy that is determined by the free carrier density, as well as the size, geometry and dielectric environment of the mode-supporting particles.Therefore, a variety of light-matter interaction processes can be boosted in the presence of LSP resonance, including photocatalysis,[202]sensing and imaging,[203-206]coherent control of electronic states,etc.[207,208]Because of the nano-femto character of LSP modes,PEEM serves as an excellent probe to study their spatiotemporal dynamics.[44,45]
3.1.1.Plasmon dynamics in isolated nanoparticles
The first conclusive demonstration of spatiotemporal ITR-PEEM imaging of LSPs was performed on periodically structured polycrystalline Ag films (100 nm wide slits with a period of 780 nm), with the obliquely excitation pulse of 10 fs, 400 nm and TM-polarization.[48]The interferometric scanning allowed the imaging of field enhancement on deep subwavelength spatial scale with 1/4 optical cycle phase resolution.Figure 3(a) shows a series of ITR-PEEM images of four LSP modes distributed vertically in the image(intensified photoemission hot spots)at increasing delay times(phase),revealing their spatiotemporal dynamics with nano-femto resolutions.It is worth noting that these modes are excited because the local nano-structures are in resonant with the excitation photon energy, and thus PEEM is very sensitive to the variations of the corresponding local electromagnetic field based on the F-D theory, (E4in the case of two-photon photoemission).At time zero, the LSP modes are coherently excited,with the phase being locked with that of the excitation light.Consequently,they exhibit strong photoemission signal when the pump and probe pulses constructively interfere(0 fs),and zero signal when they destructively interfere (0.67 fs).After the pump pulse is reflected off the surface [right panel of Fig.3(a)], the plasmons evolve into their own resonance frequency, causing the photoemission signals of these hot spots to evolve out of phase.Clearly, the maximum photoemission signal of mode A is shifted in time from that of the mode C.This is because the phase of the plasmon fields strongly depends on the geometry, size and environment of the hosting nano-structures.
Quantitative phase evolution is further extracted by analyzing the photoemission signal integrated from each hot spot as a function of delay time, as shown by the curves A-D in Fig.3(b).Clearly, mode C is nearly out-of-phase from the other modes.In addition to the photoemission intensity oscillations due to plasmon-light interference,there is also a finite DC contribution to the time dependent photoemission signal,which decays over tens of fs and represents the incoherent hot carrier relaxation in the system.[47,139]Regarding the coherent evolution,the dephasing time of these LSP modes can be extracted by fitting the correlation trace with optical Bloch equations for multiphoton processes,where a three-level system is assumed for the 2PP process.[197]In this case,the plasmon dephasing time is around 5 fs,which is shorter than the excitation pulse width.We note,however,that the optical Bloch equation fitting has a relatively large parameter space to tune,and thus may overfit the actual experimental data, especially when the contributing dynamics is shorter than the pulse duration.Nevertheless,it still serves as one of the most reasonable methods of extracting phase dynamics in nonlinear optical processes.
Besides LSPs in randomly shaped nanoparticles, predesigned nano-structures, such as circular disks,[51,59,209-211]square and triangular blocks,[212-217]and more complicated structures,[53,161,218-220]can support well-defined dipolar, quadrupolar or even higher order modes, which in principle possess different dynamical behavior.Figures 3(c) and 3(d)show a comparison of the ultrafast dynamics of two plasmonic modes.Each figure contains a PEEM image, simulated charge distribution, and the integrated ITR-PEEM trace of the dipolar and quadrupolar plasmon modes,in square gold(Au)blocks of dimension 200×200×30 nm3,excited by an obliquely incident 7 fs pulses of center wavelength of 800 nm,and polarizations of TM and TE, respectively;[209]the direction of the incoming light is indicated by the white arrow in the inset.The typical dipolar mode[right inset in Fig.3(c)]is mostly distributed at the front corners of the block with resonance wavelength of~860 nm and dephasing time of 5 fs.Interestingly, the quadrupolar modes can also be excited due to symmetry breaking of the grazing incidence angle, which showed two hot spots at the rear corners of the block[right inset in Fig.3(d)],with a resonance wavelength of~760 nm and a dephasing time of 9 fs.These modes are corroborated with calculated surface charge distributions using finite difference time domain(FDTD)method,as shown by the insets.This indicates that the charge localization at the corners of the nanostructures result in significant field enhancement for photoemission.While the resonance energy of the quadrupolar mode is lower than that of the dipolar mode,as expected from electromagnetic theory, its dephasing time is surprisingly longer.This can be understood from the fact that the net dipole moment of the quadrupolar mode is much smaller,leading to inefficient coupling to electromagnetic waves or radiative channels.In addition,the difference in the dephasing time also corresponds well with the energy spread of the respective photoelectron spectra.When the size of the nano-structures is comparable or even larger than the wavelength of light,retardation effects take place, and higher order resonances are expected,which have also been nicely imaged by ITR-PEEM.[219]
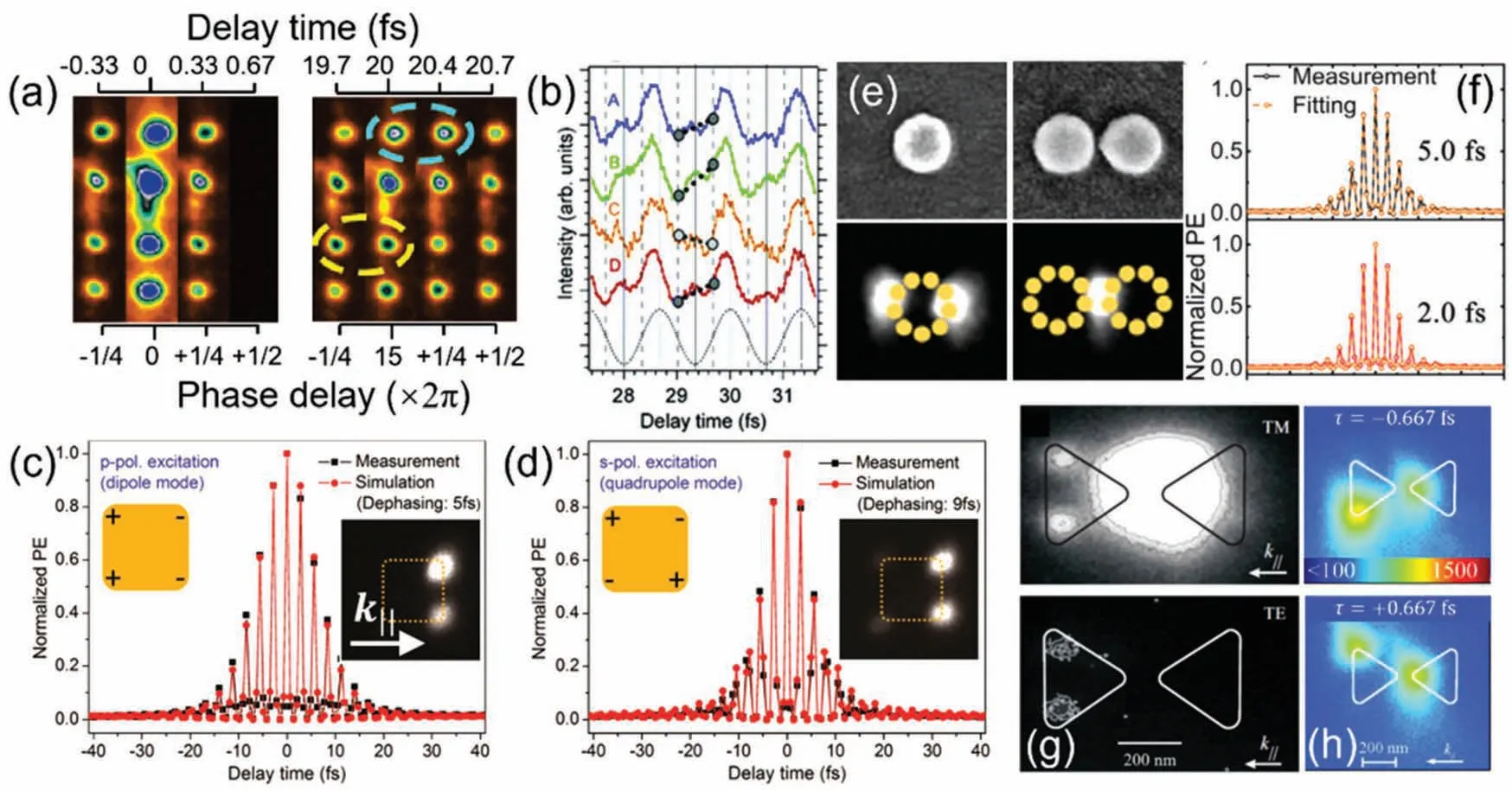
Fig.3.Ultrafast PEEM results for the imaging of localized plasmon modes.(a) Ultrafast phase evolution of selected LSPs of randomly shaped nanoparticles in silver grooves.(b)Time-dependent PEEM signals showing the temporal evolution of selected modes from(a).(c),(d)Time-dependent PEEM intensities, static PEEM imaging and surface charge distributions of plasmonic dipole and quadrupole modes under TM and TE polarized excitations,respectively. k|| indicates the projected wave vector of light on the surface.(e)SEM and PEEM images of isolated and coupled plasmonic modes in metallic nano-disks.(f) Time-dependent PEEM signals of the corresponding isolated and coupled plasmon modes, showing the correlation between plasmon dephasing time and the plasmonic coupling.(g)PEEM images of a triangular bowtie structure under TM and TE polarized excitations,demonstrating clear field enhancement at the tip of the bowtie.(h)Coherent control of the plasmon localization in a bowtie structure using cross polarized light excitation.Panels adapted with permission from: (a),(b)Ref.[48];(c),(d)Ref.[209];(e),(f)Ref.[59];(g),(h)Ref.[215].
3.1.2.Plasmon dynamics in coupled nanoparticles
When two or multiple plasmonic structures are brought close to each other with deep sub-wavelength spacing in between, coupling between the plasmonic modes take place,which offer a broad tunability of the plasmon resonance energy, spatial field distributions and dynamics.[221-225]While steady state measurements have provided a large amount of literatures of field characters in the coupled plasmonic systems,how the spatial arrangement of these nano-structures,structure geometry and other factors affect the plasmon dynamics,especially their spatiotemporal localizations are yet to be resolved clearly.
Using plasmonic circular disk and disk dimer structures,Liet al.[59]have reported the correlation between the plasmon dynamics with the size of the disk, and the size of the gap between the plasmonic dimers.The disks under investigation have a diameter and height of 175 nm and 30 nm, respectively.The excitation light was a normally incident broadband 7 fs pulse of center wavelength 800 nm.Figure 3(e)shows the scanning electron microscopy (SEM) and PEEM images for horizontally polarized excitation.The isolated disk has a strong dipolar plasmonic mode resonant at~760 nm,and the coupled disks of gap size 25 nm have a longitudinal(horizontal) mode (L-mode) resonant at~850 nm localized in the gap region; the photoemission intensity of the L-mode is enhanced by a factor of~45, or field amplitude by~1.6 for a 3PP process with respect to the incident field.Interestingly, while the dephasing time of the isolated disk is about 5 fs based on ITR-PEEM measurement[Fig.3(f)],that of the coupled plasmon mode is only~2 fs,which is reduced more than twice compared to that of the isolated disk.Moreover,it was found that there is a clear negative correlation between the gap size and the dephasing time of the coupled L-mode,such that smaller gap size leads to longer dephasing time.This can be attributed to two factors:1)the strong plasmon localization for the L-mode that enhances the radiative decay rates, and 2)the coupling between the plasmon modes of each disk also boosts the radiative decay.The individual contribution from these two factors to the relaxation dynamics is confirmed by studying the plasmonic disk dimers with horizontal and vertical polarization excitations (with respect to the image) separately.Because with horizontally polarized excitation, both inter-particle plasmon coupling and plasmon localization at the gap are present, whereas for vertically polarized excitation,the field localization at the gap vanishes by symmetry.It was found that without plasmon localization,the inter-particle plasmonic coupling can already substantially reduce the plasmon field enhancement and dephasing time.Specifically,due to the inter-particle coupling only, the dephasing time of the coupled disks of gap size~25 nm is 3.5 fs, which is 30%shorter than that of the isolated disk.When plasmon localization is included, i.e., with horizontally polarized excitation, a reduction of>50%in dephasing time was observed,which indicates that the radiative decay of coupled plasmons is further boosted by the plasmon localization.
In addition to tuning dynamical properties of coupled plasmons,the spatial distribution of plasmonic mode and their coherent control have also been demonstrated by Melchioret al.[215]using ITR-PEEM in Au plasmonic bowtie antennas.The excitation light was 25 fs, 795 nm pulse under oblique incidence.Similar to square blocks, the strongest plasmonassisted photoemission signals located at the corners of the triangular blocks, as shown in Fig.3(g), vary from TM to TE polarized light excitations.In addition, there is a strong gap mode in the bowtie gap region under TM excitation,similar to that in the coupled dimer system.
More importantly, the unique triangular symmetry properties of the supporting bowtie structure offer the possibility for coherent control of the subwavelength field distribution on the nano-femto scale.By employing a pair of coherent pump and probe pulses with orthogonal linear polarizations, it enables the spatiotemporal tunability of the location of the plasmonic hot spots as a function of pump-probe delay,as shown in Fig.3(h).Clearly, the hot spot at lower left(-0.667 fs)is shifted to the up left corner(0.667 fs)over half an optical cycle (1.34 fs) as the probe is scanned.This is because as the relative delay between the TM and TE pulses evolves,the effective total light field is switching continuously between left and right circularly polarized light,making the plasmonic excitation chiral.Therefore, the time dependent PEEM images shown in Fig.3(h) based on the coherent control concept are equivalent to static PEEM images illuminated with left and right circularly polarized light.Similar coherent control using the mixture of TM-TE light on various other structures has also been reported.[143,212,213]Therefore, it demonstrates that by combining femtosecond or few-cycle pulse excitations with PEEM imaging, one is allowed to not only study, but control on demand the spatiotemporal physics of surface plasmons.With advanced pulse shaping techniques, more sophisticated field control in a broad range of plasmonic systems will be expected.[226]
3.1.3.Plasmon-assisted coherence in 2D PEEM nanoscopy
While the discussion of the plasmonic imaging contrast so far can be described by classical electromagnetic wave interference effect,the plasmon quasiparticle,which is quantum in nature and participates in quantum transitions as bosonic particles, should not be overlooked, especially because plasmons are of great interest for on-chip quantum computing and communications.[226-228]Therefore,determining the plasmonic quantum states, or their wave packets is an essential task to understand the underlying quantum physics.[229]
A unique aspect of multiphoton PEEM experiments is that it allows the extraction of the quantum pathways of the photoemission involving plasmon quasiparticles, as well as the interaction between the plasmon-assisted intermediate states,[58]which are beyond the classical wave analysis.Preset al.[63]reported a quantum mechanical model for plasmonelectron interaction in a multiphoton PEEM experiment.In this case,the plasmon polariton state is considered as a quantum harmonic oscillator represented by occupation number state|ψ〉, and the classical polarization, which is recorded by PEEM, is described as〈ψ|b+b†|ψ〉, wherebandb†are the plasmon lowering and raising operators,respectively.The plasmon-electron interaction is then described by the HamiltonianH=g(σ+b+σ-b†)in the rotating wave approximation,wheregis the coupling constant between plasmon and electron,σ+andσ-are rising and lowering operators for electrons.The schematic of such model based on a five-level system is shown in Fig.4(a); the number of quantum levels is determined by the work function of the metal and the plasmon energy.The energy ladder of the plasmonic harmonic oscillator is shown by the parabola on the left, where the purple arrows denote adding and removing a plasmon quanta from respective state, and the dark green arrows indicate the electronic transitions in the metal.The quasi-electron energy level of the metal is shown on the right, where the plasmon model is overlaid on top of the electronic band, representing the interaction between plasmon and electron.In this five-level system,only when the electron is excited to the vacuum state|4〉,can it be captured by the PEEM objective lens for imaging.Therefore, such excitation can in principle involve multiple plasmon absorption.We emphasize that the discussion above only touches the surface of the reported model, details of the modeling of the photon energy dependent excitation pathways can be found in the original reference.[63]

Fig.4.PEEM-based coherent 2D nanoscopy of localized plasmons.(a)Schematic of the quantum harmonic oscillator model for plasmonelectron coupling.The left panel is the plasmon number state, which is overlaid on the right panel,the electronic band structure,to show the interaction between plasmon and electrons.(b)Schematic of the PEEM 2D nanoscopy experiment and an example of the LSP mode being analyzed.(c),(d)Simulated 2D rephasing spectra of the multi-and single plasmon excitations.The off-diagonal peaks, which represent the coherence between plasmon and electrons,are only present in the case of multiple plasmon excitations.All panels are adapted with permission from Ref.[63].
Experimentally, a three-pulse excitations scheme (see Section 2) is used, which is similar to that of the 2D spectroscopies[199,200]and previous PEEM-based 2D nanoscopy;[143]the observable is thus the photoelectron counts as in conventional PEEM experiment.By varying the time delays between the first and second pulse pairs,the pump and probe frequency spectra can be obtained via Fourier transformation(FT)of the respective delay axes.Consequently,the diagonal of the 2D spectra represents the nonlinear multiphoton excitations of the plasmonic excited states, and the offdiagonal signals show the coherence among the nearby states.
Owing to the superior spatial resolution of PEEM, the 2D nanoscopy can therefore capture the quantum coherence of plasmons on the nanometer scale,enabling the spatial mapping of the plasmonic coherence spectra in real space.Figure 4(b)shows the schematic of the 2D nanoscopy experiment on a slit structure of widthwand lengthLetched in polycrystalline Au film, which acts as a plasmonic resonator.Three identical and phase correlated pulses of energy 1.75 eV and pulse duration of 18 fs illuminate the entire field of view from an oblique incidence angle and excite local plasmonic fields at the coupling structure.The total surface polarization fields produce photoelectrons that can form a nonlinear photoelectron mapping as shown by the PEEM image in the top panel.Figure 4(c) shows the simulated 2D rephasing spectra based on the quantum harmonic oscillator model using experimental pulse sequencing.It contains full excitation pathways,and thus corresponds well with the experimental 2D spectra acquired by integrating within a rectangular region containing the bright hot spot at the top of the PEEM image(not shown).Clearly, a strong single plasmon excitation is observed at the diagonals in both 2D spectra at 1.75 eV, which is featured as a cross-shape distribution that cannot be reproduced by classical FDTD simulation.Surprisingly, there are also additional peaks that are present at the off diagonals of the rephasing spectra at~1.45 eV(blue circles).These are the excitations at photon energy of 5.31 eV along both the pump and probe energy axes that are backfolded into the spectral window shown in Fig.4(c).Such off-diagonal peaks can represent coherence between non-adjacent occupation number states, or coherent multi-photon excitations of electronic states in the metal.To rule out the second factor,one instead looks for single plasmon excitation [Fig.4(d)], where coupling between non-adjacent plasmonic states is strongly suppressed,i.e.,a truncated model containing only one plasmon excitation.Here,the simulation is also performed based on the experimental pulse sequencing.The residual signal comes from the coherent electron excitation due to the finite pulse width.Because the off-diagonal signal is only present when full excitation pathways exist,it therefore demonstrates that the observed off-diagonal peaks represent the coherence among the plasmonic occupation number states.Again,classical FDTD-based local response function cannot fit well the observed 2D spectra.Therefore, the PEEM based 2D nanoscopy presented above enables the coherent detection of plasmon-plasmon and plasmon-electron interactions on the nanometer scale, which, in general, can also be extended to reveal the quantum statistics of plasmon polariton states,[230]and those beyond the conventional photoelectric effect or plasmon-based emission phenomena.[231,232]
3.2.Propagating surface plasmon polaritons
Similar to LSPs, surface plasmon polaritons (SPPs)are propagating surface evanescent modes formed by coupling free-space photons with materials’ collective charge oscillations.[152]Their dispersion relation is described as/2, wherekSPPis the SPP wave vector,ωis the SPP frequency,cis the speed of light in vacuum, andεmandεdare the dielectric functions of the metal and the dielectric material that form the interface.The momentum mismatch between light and SPPs thus requires special conditions for the SPP generation, such as by slowing down light in a prism to reach total internal reflection condition, or using a geometric scatterer, such as gratings or nanoscale obstacles,that can provide sufficient photon momentum to match that of the SPPs.Interestingly,the evanescent nature of SPPs,which is due to the Landau damping of electrons in solids, forces their electric field to cycle between surface normal and surface parallel directions in the meridional plane, giving rise to a transverse pseudospin angular momentum described byS=[233-235]whereEandHare the SPP electric and magnetic field components,the star symbolizes their complex conjugates,andεandµare the permittivity and permeability of the hosting material.Unlike LSPs,propagating SPPs can transport information, which makes them promising candidates for subwavelength on-chip signal transmission and communication,[236-238]as well as quantum information processing and quantum computing.[226-228]Therefore,it is crucial to image and understand the spatiotemporal dynamics of SPPs with nano-femto resolutions, especially in the case of structured SPPs where the SPP field,phase,spin and orbital angular momentum can be engineered for functional device applications.[239,240]
3.2.1.Quasi-1D SPPs
The first ultrafast ITR-PEEM imaging of propagating SPPs was reported by Kuboet al.[49]The schematic of the ITR-PEEM experiment is shown in Fig.5(a),where the sample was composed of an~8 nm thick Ag film deposited on freshly cleaved mica substrate, and a TM-polarized, 400 nm,10 fs light pulse was illuminated on the Ag film at an angleθ= 74°from the surface normal.The line defect due to the natural cleavage of mica serves as the SPP coupling structure to match SPP and photon momenta.The Ag film was thick enough to decouple the SPPs at the Ag/vacuum and the Ag/substrate interface.As the SPPs propagate along thex-axis, their phase is stable with respect to the illuminating optical fields, allowing them to interfere and create a spatially modulated electromagnetic fields that photoemit electrons based on the F-D theory.Because of the difference in their parallel momentum, and thus wavelength, such interference forces the total polarization fieldPtotalat the surface to have a beating pattern,with the beating period of
whereλbeat,λLandλSPPare the periods of the beating pattern, light and SPP, respectively,θis the angle of incidence,andαis the angle between the wave vectors of light and SPP projected in the surface plane (xyplane).The timeaveraged PEEM intensity followsIPEEM~∫t-∞P2ntotaldt,wherenis the nonlinear order for then-photon absorption.The top panel in Fig.5(b) shows the time averaged PEEM image of the SPP beating pattern when the pump and probe pulses are temporally overlapped, which is equivalent to a single pulse excitation.The dark vertical stripe is the line defect that couples light into SPPs, and the periodic fringes are the SPP-light beating pattern.The observed beating period isλbeat~1.6 µm, which agrees well with the calculated value ofλbeat= 1.65 µm based on the Johnson and Christy’s dielectric parameters.[241]We note that the SPP wavelength, and in general the dispersion relation is dependent on the dimensionality of the SPP supporting structure and its dielectric environment.When SPPs are confined in quasi-1D wires, the plasmon dispersion, and thus the SPP wavelength,is effectively reduced when approaching to the surface plasmon resonance.[140,161,219,242,243]We note that the plasmon dispersion can also be modified via dielectric engineering, for example in molecule adsorbed metal surfaces, where the large molecular dielectric constant screens the plasmonic responses;[144,244-248]all-optical switching of SPP distribution can also be achieved with proper selection of photo-switchable overlayers.[151]What’s more,there should also be SPP waves propagate backwards from the line defect, but was not observed in this experiment.This is likely due to the limited coupling efficiency of the line defect, or the limited resolution of the PEEM instrument employed.Observation of the back propagating SPPs was achieved subsequently using welldefined coupling structures produced by lithography,[57,249,250]or epitaxial techniques.[161,219]Other advancements for enhancing SPP coupling efficiency include optimizing the structure geometry and dimensions,[142,251]or engineering periodic coupling structures[52,252-254]such that SPPs generated from each slit could constructively interfere.
The essence of time-resolved PEEM experiments is the access to the ultrafast spatiotemporal evolutions of SPPs.Figure 5(b) shows a sequence of ITR-PEEM images of the ultrafast propagation dynamics of the SPPs generated from the line defect.In this experiment, when the inter-pulse delay Δtis smaller than the pulse width, the interferometry between the pump and probe pulses creates intensity maxima and minima in the PEEM image according to the constructive and destructive interference conditions as Δtadvances.[197]Therefore,at times of constructive interferences,the observed ITRPEEM images resemble the static images, because the photoemission is dominated by the respective laser pulses and the SPPs they excite;this is the two-pulse autocorrelation regime.Beyond the autocorrelation regime,additional PEEM contrast due to the interaction between pump-induced SPPs and the probe light appears,as shown in the lower panels of Fig.5(b).These additional fringes reflect the intrinsic SPP dynamics that evolve gradually as Δtis increased; the white arrow serves to guide our eyes on the SPP propagation.The SPP fields propagate up to about 50 fs before decaying into incoherent background,after which the Δtdependent beating patterns vanish.By analyzing the motion of the beating fringes in space and time, one is allowed to obtain the group and phase velocities of the SPPs.[49,161,255]

Fig.5.Ultrafast PEEM imaging of quasi-1D propagating SPPs.(a)Schematic of the PEEM imaging contrast for imaging surface evanescent waves.Obliquely incident light field(blue)launches SPP waves(red)that co-propagate along the interface.The interfering electromagnetic waves generate the total surface polarization field that photoemits electrons for PEEM imaging.For normal incidence,the projected light wavelength becomes infinite,and the interference period becomes plasmon wavelength.(b)Sequence of PEEM images acquired at increasing pump-probe delays,showing the evolution of the SPP-light interference pattern.(c) Schematic of the ultrafast NI-PEEM imaging of a double-slit SPP interference effect.(d) Two NI-PEEM images of the SPP interference patterns at Δt=0 fs and Δt=33.3 fs.(e),(f)Experimental and simulated spatial(horizontal axis)and temporal(vertical axis)evolution of the double-slit SPP interference effect.Details of the number labeling in(d)and(f)are discussed in the main text.Panels adapted with permission from: (a),(b)Ref.[49];(c)-(f)Ref.[252].
When the excitation light illuminates from the surface normal, the observed SPP beating pattern evolves to have a period the same as the SPP wavelength.This is because the projected light wavelength becomes infinite,which effectively reduces the interference period based on Eq.(1), as detailed by Kahlet al.[155]Comprehensive understanding of normal incidence(NI-)PEEM on imaging SPPs was reported by Podbielet al.[252]where an SPP double slits experiment on Au film was carried out.Figure 5(c)shows the schematic of such experimental geometry,where SPPs are launched at both slits and propagate towards the center of the coupling structure,and the probe detects the propagated SPPs at increasing delays.Snapshots of the PEEM images at Δt=0 fs and Δt=33.3 fs are shown in Fig.5(d).There are several contributions to the PEEM image.First,two prominent photoemission signals distributed in the middle 2○and at the edges 4○of the double-slits were observed.These are static 2PP signals that are given by the simultaneous absorption of two photons from the total polarization field,which does not evolve over time.In addition,while the period in region 4○is the plasmon wavelength as determined by Eq.(1), the period in region 2○is half of the plasmon wavelength because the photoemission signal comes solely from the photoelectrons ionized by the plasmon standing waves that are spatially modulated at twice the frequency.At 33.3 fs delay time,there are two more regions having pronounced photoemission signals,as labeled by 3○and 5○.The former is due to the pump-induced SPPs from the edges being interfered by the probe light,and the latter originates from the pump-induced SPPs being interfered by the probe-induced SPP fields; these features are symmetrical with respect to the center of the double slits.
Additional features are revealed in the full time dependent PEEM measurements of the quasi-1D SPP evolutions,as shown in Fig.5(e); the corresponding simulated results are shown in Fig.5(f).Here, features 1○and 6○can be clearly seen,which are due to the self-interference of the light pulses.Finally, because SPPs can also be partially reflected from the edges,interference effect between the reflected SPPs can also be imaged by PEEM, such as features 7○and 8○.Therefore,through the analysis of different contributions in photoemission signals,it demonstrates that not only can light-SPP interference field induce photoelectrons through multi-photon absorption, pure plasmon fields themselves can also be considered as a light source for photoelectron imaging.More importantly,the different interference effects shown here are ubiquitous in most NI-PEEM experiments,[14,15,55,56,58,61,166,256-264]and thus serve as a good reference for analysis of surface polarization field beyond SPPs.There are,however,some limitations to the observation,such as the cross-polarized field coupling in the nonlinear photoemission process,especially when band structure or matrix elements of electronic transitions will be taken into consideration.This generally introduces asymmetry in the observed PEEM image but has not been reported conclusively.
Finally, we note that besides the colinear excitation schemes discussed above,spatially separated pump and probe pulses have also been employed in ultrafast PEEM imaging of propagating SPPs.[52,265]In this case,when the pump-induced SPPs enter the probe region,the interference between the SPPs and probe light produces coherent two- or multi-photon photoemission that forms the observed PEEM image.The advantage is that the probe beam is usually away from the coupling structure, such that there is no steady state plasmon signals originated from both pump and probe beams.Beyond monochromatic pump-probe excitation, two-color experiments can also be employed.[60,168,250,253,266]Such excitation scheme offers insights into understanding different quantum pathways of the underlying photoemission processes,but it also hinders the direct observation of the coherent light propagation phenomena.
3.2.2.Structured SPPs at planar surfaces
The discussion so far has been restricted to plane wave SPPs or quasi-1D propagating modes.The advantage of ITR-PEEM experiments is the visualization of the spatiotemporal evolution of the plasmonic vectorial fields in space and time with nano-femto resolutions.For example, by engineering the geometry of the coupling structures,spatiotemporal imaging of SPP wave focusing,[145,147,150]vortices,[15,55,58,61,166,259-264,267,268]and other complex interference phenomena[269-271]were achieved, offering insights into designing functional photonic devices.In addition, because SPPs can only be launched along the direction of the excitation light polarization,by changing the polarization states,one can therefore engineer and image the spatial distributions of the generated SPP fields having unidirectional SPP propagation.[255,265,272,273]When obliquely incident light has circular polarization,the unidirectional launching of SPPs can also be considered to be the demonstration of the spin-Hall effect of surface plasmons.[233-235]More interestingly, the plasmonic field and spin angular momentum (spin hereafter)vectors can be engineered to possess topologically nontrivial skyrmion and half-skyrmion textures,[14,15,61,262,264]resembling those in magnetic materials,[26,274,275,277]Bose-Einstein condensates,[278,279]liquid crystals,[280]etc.Such plasmonic topological textures may find applications in nanoscale dressing of approximate matter to drive non-equilibrium quantum states for topological quantum computing.[281]In this section,we discuss the ultrafast imaging of the plasmonic topological field and spin textures using ITR-PEEM, because the techniques involved in imaging vectorial field and spins nearly cover all that are used in the ultrafast PEEM imaging of the other structured SPP waves.
The first experimental demonstration of plasmonic electric-field(E-field)skyrmions was carried out using steady state near field measurement.[282]Here,the coupling structure is composed of that are arranged in a hexagonal geometry,with one side of the hexagon shifted by half of a plasmon wavelength to ensure the constructive interference at the center of the coupling structure.Through the interference of the SPPs generated from all slits,a 6-fold symmetric texture,as shown in Fig.6(a),was formed at the center of the coupling structure.Clearly, the texture is periodic, and within each periodic unit the field vectors wind from pointing up, to radially outward,to pointing down at the boundary, resembling a single N´eel skyrmion.The topological charge isN=1,as determined by
whereSnis the pixel-wise normalized order parameter, i.e.,electric field in E-field skyrmions.[283]We note that the plasmonic E-field textures are only transient because they evolve spatiotemporally on the nano-femto scales, so that the topology varies over an optical cycle.

Fig.6.Ultrafast vectorial PEEM imaging of structured SPP electric fields.(a)Transient vectorial electric field textures resembling that of a hexagonal skyrmion lattice.The color coding indicates the magnitude of the out-of-plane electric field.(b)and(c)PEEM imaging of the inplane(E||s)and out-of-plane(Ezs)electric fields of the skyrmion lattice.(d) Reconstructed skyrmion electric field textures at one selected time transient based on ultrafast vectorial PEEM imaging.(e)Temporal evolution of the skyrmion topological number of the electric field skyrmion lattice as a function of delay time.It shows that the topological number varies from +1 to -1 within one optical cycle.Panels adapted with permission from: (a),Ref.[282];(b),(e)Ref.[14].
Using the same coupling structure,and further developing ITR-NI-PEEM to incorporate orthogonally polarized probe fields, Daviset al.[14]have successfully imaged the vectorial field components of the plasmonic E-field skyrmions and their temporal evolution.In their experiment, the pump pulse is circularly polarized to generate the E-field skyrmion, and the probe pulses are set to be linearly polarized either in thex-ory-directions,such that only thex-ory-component of the SPP field can be interfered to form PEEM contrast;both pump and probe pulses are 800 nm in wavelength and 15 fs in pulse duration.Therefore, it allows ultrafast imaging of surface parallel fields along bothxandydirections (ExandEy); the surface-normal (Ez) field is thus obtained based on the constitution relation of the Maxwell’s equations.[284]It is important to note that because ITR-PEEM is a nonlinear microscopy technique,additional Fourier filtering was required to quantitatively extract the field amplitude;photoemission signals due to cross-polarized excitation pathways,[58,63]however,may affect quantitative analysis of the E-field amplitude.
Figures 6(b)and 6(c)show the reconstructed PEEM images of the in-plane and out-of-plane plasmon fields of the Efield textures.The complete vectorial field textures at a transient time are also shown in Fig.6(d), which agree well with the skyrmion field distribution in Fig.6(a).An important advancement enabled by ITR-NI-PEEM over steady state measurement is the observation of the time-dependent topological properties of the plasmonic E-field skyrmion lattice.Figure 6(e)shows the time dependent skyrmion topological number within~5.5 fs window.Clearly, the topological number remains at 1 for only a small fraction of an optical cycle,which quickly degrades to around zero and flips sign half an optical cycle later,averaging to zero over an optical cycle.Therefore,utilization of such field textures in tuning quantum states must be on deep sub-optical cycle time scale,potentially in nonlinear interactions with high field strength.[285,286]
Compared with the field textures, vectorial plasmonic spin textures are more robust in space and time.This is because the spin-momentum locking property of surface plasmons requires the spin direction to be associated with the timeindependent plasmonick-vector,or the energy flow of the plasmonic waves.The first observation of isolated plasmonic spin skyrmion textures [Fig.7(a)] was reported by Duet al.in a plasmon vortex carrying orbital angular momentum(OAM)of±1.[287]The OAM of a plasmon vortex is defined by the integer number of 2πphase winding of the surface-normal field component.Plasmonic,and in general optical vortices belong to a major field of structured light in optics, and for the details of the optical vortex physics we refer interested readers to excellent reviews in topical references.[239,288,289]In the case above, the plasmon vortex was generated by scattering free space vortex beam into the near field using a polymer sphere.Besides,such near field scatterer also scatters the surface plasmons into far field for optical imaging.The resulted near field images represent the contrast in the spin vectors along the surface normal, which shows a 2πwinding that is a characteristic of skyrmion textures.Interestingly, an optical spin reversal within the skyrmion texture was observed to occur on deep sub-wavelength scale of~1/60 SPP wavelength, making the plasmonic spin skyrmion useful for super resolution imaging.[290]We note that the observed spin contrast is a normalized quantity with respect to the total scattered field intensity, and thus does not quantitatively represent the plasmonic spin amplitude.
More quantitative measurements of the spin vectors, as well as the time-dependent topological number, were accomplished using ITR-PEEM technique.By coupling 550 nm,20 fs circularly polarized light with a circular coupling structure etched in Ag film, Daiet al.[61]generated ultrafast plasmonic spin skyrmion textures and performed vectorial imaging of plasmonic vortex fields; here, the vectorial imaging is achieved due to the rotation symmetry of the excitation geometry, which is different from that in reference.[14]Despite of the rotational symmetry in this case, the observed photoelectron intensity is also proportional to thenthpower of the local field based on the F-D theory, making the interference due to the SPPs and the probe light represent the amplitude of the in-plane SPP electric fields.The surface normal electric field can again be obtained via Maxwell’s equations.Consequently,the plasmonic spin vectors can be reconstructed using the vectorial electromagnetic fields based on the definition of the plasmonic spin.
Figures 7(b)and 7(c)show a pseudo-color map of the surface normal spin component,and a quiver plot of the in-plane spin components,respectively,constructed based on vectorial field imaging using ITR-PEEM;the pseudo-color in Fig.7(c)represents the magnitude of the in-plane spin.While the observed textures generally resemble N´eel skyrmion textures with radially winding spin vectors,they also have a finite tangential component,which is distinct from that of the N´eel type discussed above.Therefore,such finite tangential spin vector components confirm the observed textures to be a twisted spin skyrmion, where the twist comes from the imperfect SPP interference due to the Landau damping.In addition, the spatiotemporal robustness of the spin skyrmion is demonstrated by analyzing its topological number over the excitation pulse duration,as shown in Fig.7(d).The integer topological number starts to appear at~10 optical cycles and remains integer for about 12 cycles before vanishing to zero.This is because it takes about 10 cycles for SPPs to propagate to the center of the coupling structure where they form the vortex carrying the skyrmion texture.The textures then remain intact in space and time during the presence of the SPP vortex and evolve into rather complicated textures after the vortex is dissolved,such that the spin vectors within the original skyrmion domain have trivial textures,i.e.,zero topological number.Therefore,it indicates that the plasmonic spin skyrmion can exist as long as the duration of the plasmon wave packet,ranging from single cycle to nearly continuous wave limit.This is in stark contrast to the field skyrmion,where the topological number oscillates between positive and negative integers within one optical cycle as shown in Fig.6(e).
Besides an isolated skyrmion, three spin half-skrymions(merons)can also be created by superposition of two plasmon vortices of OAM=1 and 3.[15]Such superposition is generated by shining an Archimedean spiral coupling structure of geometric chargem=2 with linearly polarized light.Here,the geometric charge is defined by the spatial separation,in the unit of plasmon wavelength,of the starting and ending point of the spiral.Consequently,it results in an infinite number of vortices,among which three central vortices form the intertwined spin textures (Fig.7(e)) that are topologically nontrivial with a topological number of 3/2.This indicates the plasmonic system under investigation is hosting a distinct topological species that is characterized by a half integer.Interestingly,besides the spatiotemporal PEEM imaging of the vectorial spin textures,an important physical quantity,the optical linear polarization singularity,[291,292]can be introduced to describe the topological spin textures.The linear polarization singularity is defined to be the spatial region where the in-plane electric polarization is linear.Because it typically has a contour distribution in space and usually forms closed loops, it is thus referred to as L-lines.Besides,the plasmonic L-line distribution in fact defines the boundary of skyrmions, within which integer or half integer topological number can be obtained; it corresponds to the equator of the polarization Poincar´e sphere.This is because the plasmonic electric field revolution vanishes in the surface plane, making the spin vectors to be purely inplane.In case of the vortex superpositions, the calculated Lline distribution is shown as the grey contour in Fig.7(e).Experimentally, the ultrafast spatiotemporal evolution of the Llines enclosing three plasmonic spin half-skyrmions can be reconstructed from the vectorial imaging of the plasmonic fields using ITR-PEEM,where the extraction of the plasmon polarization ellipse was achieved through Horn-Schuck method.Figure 7(f) shows the experimental L-line distribution based on ITR-PEEM imaging that is averaged over 10 optical cycles,which agrees well with that obtained from the FDTD simulation [Fig.7(g)].Therefore, the observed L-line distribution serves as an excellent indicator of the plasmonic spin textures.More importantly,there also exists L-lines that dissect regions of opposite surface normal spin components,such that optical spin reversal can occur on nanometer scale or smaller.[61,264]While the instrumental resolution is limited to capture such atomically sharp spin reversal, it could offer a new pathway for controlling electronic spin degrees of freedom in the quantum regime on the scale that is comparable to or smaller than that of the electronic wave function.[281]

Fig.7.Ultrafast vectorial PEEM imaging of structured SPP spin textures.(a)Schematic of an isolated skyrmion texture.The labels r1 and r2 denote the radius within which the topological number is 1/2 and 1.(b)and(c)Normalized surface normal Sz,n (color)and surface parallel S||,n (arrows)spin components derived from ultrafast NI-PEEM imaging.The color coding in (c) represents the magnitude of the in-plane spin component.(d) Timedependent topological charge of the isolated plasmonic spin skyrmion.(e) Vectorial distribution of plasmonic spin merons along with its topological boundary(grey contours)determined by the linear polarization singularities.(f)and(g)Ultrafast PEEM imaging and the corresponding simulation of the linear polarization singularity of the plasmonic merons.Panels adapted with permission from: (b)-(d)Ref.[61];(e),(g)Ref.[15].
Finally, the idea of plasmonic or optical skyrmions has been largely extended to several optical media, including surface plasmons,[262,264,293-297]spoof plasmons,[298,299]freespace light[300-304]and others.[305,306]Regarding their interaction with matter or driving excited quantum states on the nanofemto scales,plasmonic field and spin textures have a unique advantage.They have deep subwavelength variations down to sub-nanometer scale,which provide new avenues to create and coherently control non-equilibrium quantum matter at the atomic limit,from EUV to the terahertz frequencies.[93,106,307]The core of plasmonic skyrmions is also known to be the focus of parallel electric and magnetic fields,which is essential in driving magnetoelectric effect[308-310]and may pertain to the detection of axion quasiparticles.[311-313]
3.3.Propagating photonic modes
Beyond plasmonic responses, PEEM also enables the nano-femto imaging of waveguided modes when free-space light is confined into or close to dielectric materials.These modes are in general not confined to material surfaces, and thus can propagate into the bulk of the supporting materials.Prominent examples include optical modes supported by silicon photonic waveguides and indium tin oxide (ITO).These electromagnetic modes are building blocks for on-chip information processing.Beyond optical modes, coupled lightmatter wave excitations, such as phonon polaritons, can also propagate in the bulk, and in principle, can be imaged by PEEM at the surface.But such experiments are yet to be explored.
Here, we show two examples of PEEM imaging of photonic modes at material surfaces.The first example is the waveguide mode in conducting ITO thin films.[56,148,314]Figure 8(a) shows the PEEM image of an ITO sample under cw UV light illumination.[314]A deep slit (dark horizontal contrast) and a shallow trench (labeled by B) for producing the waveguided modes were etched in the film.When illuminated by 410 nm, 80 fs pulses under oblique incidence condition,the observed PEEM images have clear periodic patterns similar to the interference fringes observed in the case of propagating SPPs.Unlike SPPs, which can only be excited by TM light, both TM and TE light pulses can produce clear interference fringes, as shown in Figs.8(b) and 8(c).It thus suggests the observed fringes have a different origin.In addition, counter propagating waves were also visible in these experiments.As confirmed from numerical calculations,such fringes were attributed to the interference between the waveguided mode and the external light field.This is further followed by experiments in halide perovskites[315]and transition metal dichalcogenides,[77]demonstrating that PEEM is capable of imaging electromagnetic modes beyond SPPs.
The other photonic mode that is ubiquitous to PEEM imaging is the quasicylindrical waves (QCWs).[251,316,317]A nice example of PEEM imaging of QCWs was carried out on semimetal Cd3As2.[318,319]We note that Cd3As2is categorized as a Dirac semimetal,[320]but its unique band structure has little to do with the QCW phenomenon discussed below.Figure 8(d) shows the SEM image of the Cd3As2thin flakes exfoliated on silicon substrate.When 400 nm, 100 fs light pulses illuminate such flake from the surface normal,periodic fringes are observed along the direction of the light polarization,as shown by the periodic fringes in Fig.8(e).Because the surface plasmon resonance of Cd3As2is in the mid-infrared regime, it therefore confirms that these fringes cannot be attributed to SPP excitations at the material surface.Instead,by analyzing the dispersion relation of the periodic fringes,it shows that they originate from the QCWs scattered from the material edges.As these QCWs propagate,they interfere with the light beam to create the observed interference pattern.By tuning the polarization direction, the direction of the QCWs can be altered correspondingly.This observation is also well reproduced by classical electromagnetic wave simulations.It is important to note that QCWs can be generated at nanoscale obstacles in most materials.[316,317]Therefore, care must be taken when analyzing fringe contrast in PEEM images,particularly when multiple interference effect may occur.

Fig.8.PEEM imaging of nanoscale photonic modes.(a) PEEM image of a structured ITO thin film under mercury lamp illumination.Region A labels the pure ITO thin film.Regions B and C label the shallow and deep trench produced by focused ion beam etching,respectively.The arrow denotes the incident light direction.(b)and(c)PEEM imaging of the photonic modes confined in the ITO thin films under TM and TE polarized light excitation.(d)SEM image showing the Cd3As2 thin flake for QCW excitation shown in(e).(e)NI-PEEM imaging of the QCW on the surface of Cd3As2, where the red arrow denotes the excitation polarization.The QCW are dominantly excited at edges that are perpendicular to the excitation light polarization.Panels adapted with permission from:(a)-(c)Ref.[314];(d),(e)Ref.[319].
3.4.Hot electron dynamics
Quasiparticle dynamics plays an essential role in condensed matter physics, but has been mostly studied based on far field spectroscopic methods, such as time resolved optical absorption and reflection, time and angle resolved photoelectron spectroscopy, etc.[92]While the time-resolving capability of these techniques can nicely capture the spaceaveraged, macroscopic quasiparticle properties, investigation of their creation, interaction and annihilation on the nanofemto scale is still technically challenging.Despite so,understanding local electronic properties of matter is of significance because it allows one to correlate quasiparticle properties with other degrees of freedom in solids,such as impurities,[321,322]strain[323,324]domains,[67,68]etc.Therefore, it is crucial to study the quasiparticle physics on its intrinsic spatiotemporal scales, which will pave the way for designing new functional devices where quantum effects dominate.
3.4.1.Spatiotemporal evolution of electrons
Ultrafast imaging of spatiotemporal electron dynamics was first achieved by two-color time resolved PEEM by Fukumotoet al.on GaAs(100) surface.[72]In this experiment,charge carriers injected by 2.4 eV pulses were observed to laterally transport and recombine on picosecond time scales,with a transport rate tunable by an external voltage.While the spatiotemporal resolution was limited,it demonstrated the potential for TR-PEEM to be employed in studying quasiparticle dynamics with nano-femto resolutions.
In 2017, Manet al.[73]reported a TR-PEEM study on the vertical and lateral charge transfer in a semiconductor heterostructure composed of bulk GaAs and thin flake n-dopedγ-InSe, with a significant improvement in the spatial resolution.In such heterostructure,type II band alignment is formed,because the band gaps of GaAs andγ-InSe are 1.42 eV and 1.25 eV respectively; the band gap ofγ-InSe also decreases with increasing flake thickness.Consequently,the global conduction band minimum (CBM) lies in the bulkγ-InSe, while the valence band maximum (VBM) is located in GaAs, as shown in Fig.9(a).A steady-state PEEM image of such heterostructure sample under UV light illumination is shown in Fig.9(b),where regions ofγ-InSe of different thicknesses are labeled.
In the ultrafast PEEM imaging experiment, the pump pulse has a wavelength of 800 nm and pulse duration of 45 fs,and the frequency tripled 266 nm serves as the probe; both light sources illuminate the entire field of view of PEEM from a grazing angle.At the inter-pulse delay Δt=0 ps, photoexcitation produces non-thermal electrons in the respective conduction bands of GaAs andγ-InSe,such that electrons in GaAs are 0.4 eV higher than those inγ-InSe.Within a few ps delay,clear electron gain is observed in allγ-InSe regions and slight loss is seen in the GaAs region, as shown in the sequence of PEEM images in Fig.9(c);the raw PEEM image at Δt~500 fs was subtracted to emphasize the electron gain and loss.This represents the population of the conduction bands ofγ-InSe in the heterostructure sample.At 10 ps and longer,electrons continuously accumulate in the thick InSe region(red),accompanied by a depletion of electrons in both the GaAs and the thin InSe regions.This is because of the charge transfer from these regions to the thick InSe region, where the global CBM resides.Correspondingly, quantitative analysis (not shown) of the photoelectron rise time shows that it is the longest in the thickγ-InSe region,as electrons from all other regions eventually sink to the global CBM.When Δtis further increased,depletion of electrons in the thickγ-InSe is observed,which indicates that electrons have recombined with holes and relaxed to the ground state.Finally,we emphasize that the charge transfer mostly occurs at the interface of the heterostructure,thus it is mostly vertical and not spatially resolved by PEEM.The lateral transfer from thin to thickγ-InSe region contributes only a small fraction.

Fig.9.Ultrafast PEEM imaging of hot electron dynamics in layered semiconductors.(a)Energy level diagram showing the mismatch of the conduction and valence bands of the semiconductor heterostructure composed of γ-InSe and GaAs.The bandgaps of GaAs and γ-InSe are 1.42 eV and 1.25 eV,respectively.The global CBM and VBM are located in γ-InSe and GaAs, respectively.(b) PEEM image of the InSe/GaAs heterostructure under mercury lamp illumination.(c)Ultrafast PEEM imaging of the charge transfer dynamics in the heterostructure,revealing that the photoexcited electrons are mostly accumulated in the thick γ-InSe with global CBM.(d)Pixel-wise analysis of the ultrafast PEEM intensity evolution of a monolayer WSe2.Strong sample inhomogeneity in terms of electron dynamics is observed,as evidenced by the electron relaxation traces acquired at four different spots on the sample (inset PEEM image).(e) Spatial mapping of the fast and slow decay constants extracted from the PEEM intensity evolution in (d),showing strong inhomogeneities in the carrier lifetimes.(f)The corresponding non-Gaussian statistics of the carrier lifetimes in(e).Panels adapted with permission from: (a)-(c)Ref.[73];(e)-(f)Ref.[76].
With such demonstration, it is clear that ultrafast PEEM is capable of imaging the vertical and lateral charge transfer processes with nano-femto spatiotemporal resolution.In fact,similar charge migration processes have already been reported in bulk semiconductors,[325]molecular[326,327]and other van der Waals heterostructures.[328-330]While literatures focus on the intrinsic electronic properties of certain materials,it is interesting to note that micron-sized layered materials with sophisticated gate structures can also be investigated in ultrafast PEEM.In this case, one can expand the problem space into gate-controlled quantum states, such as strong correlations and ferroelectricity that are observed in graphene and TMD heterostructures.[331-336]
3.4.2.Electronic inhomogeneity
An important question in material science and device fabrication is the homogeneity of the electronic properties of the materials being used.This is evidenced by the matureness of the semiconductor industry nowadays, where high quality silicon and gallium arsenide are pursued.In the scientific research community, the thin film samples under investigation can be produced in several ways, including thermal evaporation, atomic layer deposition, photoinduced layer deposition, molecular beam epitaxy, chemical vapor deposition(CVD) and others.Among these techniques, CVD is one of the most commonly used material growth techniques used in research labs[337]because of its relatively simple growth environment and low cost.In addition,since the successful fabrication of graphene, scotch tape exfoliation is also becoming a major method for preparing high-quality layered materials.Such method,however,has limited potential in producing wafer scale layered materials.[338]
Regarding CVD method, it is well known that a significant number of defects,[339]compared with tape-exfoliated samples, can be introduced in the material.Therefore, it is important to understand the inhomogeneity of electronic properties of CVD grown samples, which requires careful nanofemto characterization other than the far field microscopic probes.Using TR-PEEM, Wanget al.[76]reported the spatially inhomogeneous carrier dynamics in CVD grown monolayer WSe2on SiO2/Si substrate.In this experiment, a 46 fs,2.41 eV pump pulse was used to generate hot electron distributions in WSe2.In addition, a probe pulse of 40 fs and 3.61 eV was used for photoionizing electrons near theΓpoint of the Brillouin zone for PEEM imaging.A representative PEEM image under two-photon excitation is shown as the inset in Fig.9(d).Clearly, the photoelectron intensity varies within the triangle monolayer sample.When varying the interpulse delay Δt, one obtains a sequence of TR-PEEM images,from which time-dependent photoemission yield can be extracted down to a single pixel level.Figure 9(d) shows four photoelectron intensity evolution acquired at the corresponding spots in the inset PEEM image.The photoelectron dynamics show a clear two-step behavior,with the characteristic time constants to be aroundτ1~30-130 fs andτ2~1-3 ps.This conclusively demonstrates that a strong inhomogeneity of the electronic properties exists in the CVD grown monolayer.Here,the faster and slower components of the time-dependent photoelectron intensity are attributed to the intervalley scattering and exciton-exciton annihilation,respectively.The former occurs on tens of femtosecond scale to cause electron momentum relaxation,i.e.,redistributing the initially non-thermal electrons to form a quasi-thermal equilibrium.The latter is a many-body excitonic analog of the Auger process of highly excited electrons.Specifically, in monolayer TMDs where screening is reduced and many-body interaction is strong,the electron and hole of an exciton can be easily destroyed and transfer their energy to another exciton,such that their dynamics has a quadratic dependence on the exciton density.
By fitting the electron dynamics in a pixel-wise fashion,a spatial mapping of the obtained time constants of the two electron relaxation channels can be extracted, as shown in Fig.9(e), along with the corresponding statistics in Fig.9(f).Importantly, the PEEM intensity, as well as the corresponding electron dynamics, vary significantly from spot to spot.Based on the non-Gaussian histogram of the extracted relaxation constants,different conclusions about the relaxation dynamics can be drawn, with a difference as large as a factor of ten, indicating strong inhomogeneity of sample electronic properties.Besides, the intervalley scattering process is observed to be accelerated at the peripheral edges of the sample,i.e.,the edges have clear blue color contrast,which is because of the stronger electron-phonon interaction assisted by structural disorder induced phonon modes.Correspondingly,such disorders also reduce the exciton diffusion,resulting in largerτ2,as shown in the right panel of Fig.9(e).Therefore,the spatiotemporal imaging of the hot electron dynamics not only provides quantitative understanding of the inhomogeneity of the material electronic properties, but also emphasizes that care must be taken when drawing conclusions about macroscopic electronic properties.Research regarding the electronic inhomogeneities is continuously growing based on TR-PEEM technique.[74,77,80,328,340-342]
3.5.Magnetization dynamics
Magnetism is a major part of research of the modern condensed matter physics.Not only does it relate to the fundamental problems such as magnetic exchange interactions and spin-orbit interaction of electrons,[343]it also pertains to key technological applications including magnetic recording and memory devices.[344]The later mostly rely on the nanoscale spin reversal and spin canting, which have an intrinsic time scale on the order of nanoseconds in conventional ferromagnetic materials.[345,346]Therefore,it is important to develop an experimental technique that can resolve the spin and magnetization dynamics on their intrinsic spatiotemporal scales.
Methods for characterizing magnetizations in real space are mostly based on spin-dependent optical effect, such as magneto-optical Kerr effect (MOKE) imaging where the polarization and intensity of light are modified,[347,348]or circular/linear dichroism (CD/LD) effects where absorption coefficients of photons of opposite helicities differ.[349]While time resolved MOKE microscopy can resolve magnetization domains on the ultrafast time scales depending on the pulse duration, its spatial resolution is restricted by the Abbe limit of the light source being used.[348]In the case of CD effect,circularly polarized x-ray pulses can be used to show elementspecific magnetic contrast, especially with spatial resolutions when combined with PEEM.[350-354]In the x-ray illuminated PEEM, the number of the resulted secondary electrons from circularly polarized excitation is proportional to the projection of magnetization along the spin of light (σ+/-), i.e.,M·σ+/-,whereMrepresents the magnetization.Therefore,the analysis of photoelectron counts as a function of light polarization andk-vector offers a unique way of acquiring the vectorial surface magnetizations with nanometer resolution.Therefore, using x-ray CD effect to probe magnetism with PEEM instrument is termed as XMCD-PEEM.
Conventional XMCD-PEEM experiments are conducted in synchrotron facilities where high photon flux x-ray is readily available.[355-358]To resolve the ultrafast spatiotemporal evolutions of the magnetization, however, requires further technological innovation in the pump-probe scheme.Particularly,unlike conventional pump-probe techniques where two light pulses are used, a pulsed magnetic field of hundreds of picoseconds is used to act as the pump source to initiate spin precession.[67,70]With such ultrafast stimuli, important questions in magnetic materials,such as the evolution of magnetic domain walls,vortices and spin textures,can be readily accessible.
Figures 10(a)-10(c) show an example of time resolved XMCD-PEEM imaging of magnetic vortices in a 2×1 µm2CoFe block of 20 nm thick.[67]A magnetic vortex is a 3D magnetic structure that has curling in-plane magnetizations around a nanometer-sized core,where the magnetization turns out-of-plane [Fig.10(a)]; the handedness of the vortex is determined by the direction of the out-of-plane magnetization at the core.[359,360]By applying an in-plane magnetic field pulse [gray arrow in Fig.10(a)], it initiates a vortex core displacement, after which a gyration motion occurs due to the magnetostatic field induced by imbalanced magnetization.Clear visualization of the vortex core redistribution is shown in Fig.10(b) at different time delays, where the yellow arrows mark the vortex locations.In these PEEM images, the contrast around the core represents the projection of magnetization along the spin of the incident x-ray photons, revealing quantitatively the vectorial magnetization directions on the surface.By varying the time-delay of the magnetic field pulse and the probe x-ray,and analyzing the core locus in a time window spanning over 8 ns, one reveals the complete evolution dynamics of the vortex core,as shown in Fig.10(c).Therefore,a quantitative determination of the vortex speed of~100 m/s can be achieved,leading to the conclusion that the vortex core region has considerably high magnetic field of~80 mT that leads to the observed dynamical behavior.
An important question other than magnetic vortex core is the domain wall evolution.We show an example of time resolved XMCD-PEEM imaging of the domain and domain wall dynamics in micron-sized permalloy square (Ni81Fe19)of length and thickness of 6 µm and 30 nm, respectively.[70]The three panels in Fig.10(d) show the raw XMCD-PEEM sequence, the net change in the PEEM intensity obtained by subtracting the dynamical PEEM image from that at equilibrium, and the schematic of the magnetization dynamics, respectively.Here, the pump magnetic field pulse was about 60 Oe with rise and fall times about 150 ps and 300 ps, and the probe pulse is~70 ps x-ray produced by isolated electron bunch.The directions of the pump and probe fields are shown in Fig.10(d)asHpandP,respectively.
Firstly, the observed XMCD-PEEM images show clear vortex-like magnetization configuration (top row), a characteristic of the so-called Landau flux-closure pattern,[361]as also shown in Fig.10(b).Before magnetic field excitation,the PEEM image[upper left of Fig.10(d)]shows a clear curling of the magnetization distribution.When pumped out of equilibrium,the domains having magnetization perpendicular toHpare observed to have spin precession parallel toHpdue to the magnetic torqueM×Hp, with a precession frequency~1.9 and 2.4 GHz; at longer time, such precession relaxes back to equilibrium based on a magnetic dipole interaction.Subsequently, the domain walls are distorted periodically with a frequency of~230 MHz, and the vortex core starts to displace perpendicular toHp.Such dynamical behavior is more pronounced in the difference PEEM images(middle row).The corresponding magnetization configurations are shown in the bottom row of Fig.10(d).We note that a linear displacement of the vortex core, instead of gyration is observed in this case,most likely because of the offresonant field excitation.[362,363]In this case,the stroboscopic PEEM imaging of magnetic structure evolution allows precise measurements of the speed of the vortex motion, as well as the eigenmodes of the domain wall oscillations,providing further understanding of the magnetic dipolar interactions on the nanometer scale.

Fig.10.Ultrafast PEEM imaging of magnetization dynamics.(a)Schematic of the magnetic vortex structure.The magnetization directions, the spin precession torque, the pump magnetic field direction and handedness are labeled by the white arrows, the blue arrows, the purple arrow and the hand symbol, respectively.The central surface-normal spin is also shown by a green arrow.(b)XMCD-PEEM images of the vortex displacement in CoFe block.Yellow arrows mark the locations of the vortex core.(c)Temporal evolution of the vortex core as a function of pump probe delay times,extracted from a sequence of XMCD-PEEM images.(d)Top:sequence of XMCD-PEEM images of a square Ni81Fe19 block.Middle:difference intensity images at the same time steps obtained by subtracting the corresponding XMCD-PEEM image in the top panel from the equilibrium image (left most in top panel).Bottom: the schematic representation of the magnetization(arrows)configurations at each time step.The directions of the magnetic stimuli and the probe pulse are shown in the middle panel.The displacement and distortion of the domain walls,as well as the vortex core,are mostly visible in the difference intensity maps in the middle panel.Panels adapted with permission from: (a)-(e)Ref.[67];(d)Ref.[70].
The applications of XMCD-PEEM so far have been mostly conducted based on a magnetic field pump source of~100 ps long,which prevents the extraction of the many-body interactions among charge,lattice,spin,and orbital degrees of freedom that occur on much shorter time scales.By employing femtosecond pump pulses and a spin-polarized electron detector,[364,365]one can in principle significantly boost the time resolution of detecting spin dynamics using TR-PEEM technique.Another promising aspect lies in the development of the high repetition rate, high photon flux table-top x-ray sources based on HHG processes.[366,367]These photon sources not only offer tunable photon energy of tens of eV,but also ultrashort pulse duration down to~10 fs.When combined with fs circularly polarized pump light,they can serve as an excellent tool in studying ultrafast (de-)magnetization dynamics with nano-femto resolutions.Therefore, the concept of time resolved XMCD-PEEM, along with the instrumental technical developments, is an excellent platform to study spin and magnetization physics on the nanometer spatial scale,and nanosecond to femtosecond temporal scale,exploring new spin-based functional applications beyond ferromagnetic spintronic devices.[368,369]
4.Imaging electrons in momentum space
While the majority of the ultrafast PEEM studies have focused on the real space imaging of excited states phenomena,the development of the PEEM electron optics, particularly in improving electron energy and momentum resolution,has matured the imaging of photoelectrons in the momentum space,turning PEEM into a momentum microscope.Together with ultrafast light sources and the PEEM objective lens, it essentially serves as an ideal tool to probe unoccupied electronic structures of atomically thin,microscale samples.[43]
A model problem in time-resolved momentum space imaging is the visualization of excited atomic or molecular orbitals in the momentum space, such as in crystalline molecular films of 3,4,9,10-perylene-tetracarboxylicdianhydride(PTCDA),[91]pentacene[89,370]and C60.[371]This is because molecular orbitals,and particularly the highest occupied molecular orbital(HOMO)and the lowest unoccupied molecular orbitals (LUMO) are key elements in determining the electronic properties in bond forming and breaking, and chemical reactions.[372]Moreover, with the large momentum space accessibility, ultrafast MM can also be applied mostly in visualizing the charge and excitonic properties of transition metal dichalcogenides,[32,81,83,86,88,164,373-377]These studies provide unique information in the many-body excited state physics,including momentum-forbidden dark excitons,interlayer moir´e excitons, exciton momentum and effective mass,etc., all of which are inaccessible from conventional ultrafast optical spectroscopies.Finally, with the success of the TR-MM,broader material systems are being investigated,including Dirac materials, such as graphene,[182]topological materials,[87]correlated materials possessing charge density wave orders,[33,378-380]and others.[90,381]It thus makes TRMM a technique that can be widely applicable in the condensed matter research community for studying full Brillouin zone electronic properties in both steady and excited states.
4.1.Molecular orbitals
Molecular orbitals naturally bridge the momentum space electronic properties of molecules with their electronic wave function distribution in real space,making them attractive for chemists and physicists for the study of many-body interactions on the single molecule level.One promising technique in resolving the frontier orbitals is steady state ARPES,because the momentum space distribution of photoelectrons is essentially a Fourier transformation of the real space wave function of the corresponding molecular orbital, contingent on a few symmetry and energy restrictions being satisfied; such technique is termed as the orbital tomography, or photoemission tomography.[382-384]
While conventional photoemission tomography can only acquire occupied molecular orbitals, leaving the study of LUMO inaccessible.The imaging of LUMO and their femtosecond dynamics can be achieved by the EUV probed ultrafast ToF-MM.Wallaueret al.[91]first demonstrated the excited electron distributions in the LUMO of PTCDA molecules grown on oxygen-covered Cu(001) substrate.The molecules are aligned both along and perpendicular to the lattice orientations of the substrate, such that the adsorbed PTCDA molecules have two orthogonal orientations along (110) and(¯110) axes.In this experiment, the pump and probe pulses have photon energies of 2.3 eV and 21.7 eV, with incident directions indicated by the green and purple arrows, respectively, in the top right of Fig.11(c).The MM imaging of the LUMO and HOMO electron distributions at three selected pump-probe delay times Δtare shown in Figs.11(a)and 11(b),respectively.At Δt=-46 fs, the one-photon photoemission reveals the HOMO electron momentum distribution at-2.18 eV below the Fermi level, while photoelectron signal 0.45 eV above the Fermi level is within the noise level.At Δt=93 fs,pronounced electron distribution is observed in the LUMO of PTCDA,featuring a distinct four-fold symmetry in the constant energy map.Such electron signal exists for about 200 fs before the system relaxes to the ground state.
To gain further insights into the observed time-dependent orbitals, the real space Kohn-Sham orbitals of the corresponding LUMO and HOMO were calculated and shown in Figs.11(c)and 11(d),for two different molecular orientations,along with their momentum space distributions.Because of the grazing incidence,clear asymmetry is observed in the electron distribution.The superposition of the molecular orbitals of the orthogonally distributed molecules are shown on the right, which has a clear four-fold symmetry, with the intensity amplified at the top left corner of the momentum space.This agrees well with the experimental findings in the TRMM spectra.We note that this observation does not involve the phase information of the molecular orbital,which is an essential ingredient for extracting the electronic wave function in real space,as has been discussed in detail in steady state photoemission tomography literatures.[82]By tuning the direction of light incidence and polarization, it was demonstrated that excitation of molecules of certain orientations can be achieved,allowing the extraction of different real space photoemission pathways for PTCDA molecules.Besides, an unexpectedly long coherence time was also observed between the LUMOHOMO states, which can be attributed to the direct HOMOLUMO transition aided by the electron-induced polarization field along the molecular long axis.
Beyond the LUMO-HOMO electronic transition in a model molecular system, TR-MM is also sensitive to a variety of electronic phenomena in molecular solids.For example,the molecular exciton doubling process due to singlet fission in pentacene molecules has been visualized both by EUV and free-electron laser probed TR-MM microscopes,revealing the ultrafast evolution of the exciton orbitals and their localization in space.[89,370]Moreover, the multi-orbital character of C60orbitals,as well as the associated electron and exciton dynamics have also been reported.[371]Therefore,despite the fact that TR-MM applications are still in infancy,one can already expect it to be largely employed to surface chemistry and surface physics in the near future, focusing on a broader range of scientific problems including, but not limited to intra- and inter-molecular charge and energy transfer,molecular orbitalvibrational mode coupling and beyond.[385]

Fig.11.Ultrafast momentum microscopy imaging of molecular frontier orbitals.(a) and (b) Time-resolved MM images of LUMO and HOMO of PTCDA molecules in the momentum space at constant energies of 0.45 eV and-2.18 eV from the Fermi level,respectively.Clear four-fold symmetry due to the surface molecule orientations is observed.The intensity asymmetry is due to the grazing incidence angle of photons, with their incidence directions shown in(c).(c)and(d)Calculated Kohn-Sham orbitals of the LUMO and HOMO in both real(left)and momentum spaces(right).The real space orbitals are considered for molecules of both surface orientations,and the momentum space imaging is the superposition of both.The directions of the pump and probe pulses are indicated by color coded arrows in(c).All panels are adapted with permission from Ref.[91].
4.2.Exciton in van der Waals materials
Excitons are neutral composite quasiparticles composed of an electron and a hole.[386,387]They usually exist in materials with moderate bandgaps, or energy gaps, and small dielectric screening, such that the strong Coulomb interaction between the electron and hole is sufficient to create a new bound state that is against thermal fluctuations.Because of their neutral and bosonic character,excitons have great potential in coupling with electromagnetic fields, serving as efficient sources of quantum light.[388-390]Typically,bright excitonic emission is based on the fact that the electron and hole composing the exciton have the same quasi-momenta,making direct transition and coupling to photons efficient.Regarding material systems that host interesting exciton physics, a renowned category is the layered TMDs.[391,392]They are featured by the strong quantum confinement effect and reduced screening, which can lead to direct excitons with large binding energies in the monolayer form.Therefore,photoluminescence and absorption spectroscopies are ideal tools to probe the associated direct exciton emission.There is, however, a variety of other excitonic species,such as momentum-indirect(electron and hole have different quasi-momenta) dark excitons,charged excitons,and others,which also play major roles in the many body physics of the associated materials.Studying these excitonic species with momentum resolution,unfortunately, cannot be easily achieved by optical probes, mostly because the photon momentum is too small to allow the access of electrons in the entire Brillouin zone.
To gain insight into the exciton physics spanning the entire momentum space, TR-ARPES is the to-go technique,which can probe excited electron-hole pairs with superior time, energy, and momentum resolutions.In conventional TR-ARPES experiments, macroscopic samples are required,which are either bulk, or monolayers produced by epitaxial growth on gold or graphene substrate.For bulk samples,the layer dependent electronic structures and efficient screening prevents the detection of the intrinsic excitonic response of monolayer TMDs.[84,375,393-395]In the case of epitaxially grown samples, TR-ARPES has been applied to study their charge carrier and exciton dynamics,[396-400]but the control of crystal(valley)orientations remains challenging.In addition,large scale TMD monolayers produced by gold exfoliations have also been achieved,but its sample inhomogeneity results in significant spectroscopic broadening.[401,402]Regarding the study of high quality tape-exfoliated samples, a microscopic time resolved ARPES is required, bringing TR-MM to the forefront.
The full-momentum imaging of ultrafast exciton formation and relaxation dynamics using TR-ToF-MM was demonstrated by Mad´eoet al.in monolayer WSe2.[81]In this experiment, the high quality WSe2monolayer (1L) was placed on highly doped silicon substrate with a thin insulating h-BN layer to prevent charge transfer between WSe2and the substrate.The pump pulses are tunable in the visible regime,and the probe pulses are EUV light of 21.7 eV generated from gas-phase HHG; both light pulses are of~200 fs.The sample under investigation was at 90 K.In 1L-WSe2, two types of exciton species can be formed, 1) the direct exciton at theK(K′) point of the Brillouin zone corner, and 2) the momentum-indirectK-Qexciton that have large momentum difference in their electron and hole constituents.When using above bandgap excitations (2.48 eV), both excitons can be generated, as shown by the time-dependent MM image in Fig.12(a).Specifically, before time zero, only the 6-fold symmetric VBM signal is visible(grey contrast in Fig.12(a)).When pump and probe pulses are temporally overlapped,electrons are both populated in the K andQvalleys of the conduction band(blue and red regions),which evolve to be more pronounced after 0.5 ps.Clearer visualizations of the photoemission spectra parallel to theK-Qdirection for selected time steps are shown in Fig.12(b), along with the calculated band structures overlaid on theE-kmap.The observed photoelectrons mostly reside in theKandQvalleys, with their energies~400 meV below the CBM at Δt ≥0.3 ps.This confirms their excitonic nature rather than electron plasma in the conduction bands.To quantify the exciton formation dynamics, Fig.12(c)shows the evolution of the exciton density(top)and the average electron energy(bottom)in theKandQvalleys.Immediately after photoexcitation, electrons in both valleys have energy~1.9 eV above the VBM,which indicates that these signals come from hot electron plasma,and excitons have yet to be formed on such short time scale.As the pump and probe delay time increases, the hot electrons cool down by~0.15 eV to form the corresponding exciton bound states on~0.3 ps scale,which are~390 meV and 480 meV below the corresponding conduction band minima.Correspondingly,the exciton density also reaches a maximum on a similar time scale.Subsequently, both direct and indirect excitons decay and form a quasi-static distribution before being fully recombined at longer time delays.The full photoelectron energy spectra as a function of delay times of theKandQvalleys are shown in Fig.12(d),where distinct energy relaxation processes are visible, representing the ultrafast formation of the direct and indirect excitons.
When the material is under resonant pumping(1.72 eV),theK-valley direct exciton dominates the photoemission spectra at zero delay.With increasing Δt, the nearly degeneratedQ-exciton gets populated after~400 fs due to the phononassisted intervalley scattering fromKtoQpoint.Subsequently, the indirectQexciton serves as an electron reservoir for theKexciton, prolonging relaxation times of direct and indirect excitons to be~1.7 ps and~2.5 ps, respectively.We note that such conclusion can only be drawn indirectly based on optical measurements, because theQexciton is not detectable.Further studies by Wallaueret al.in the case of WS2monolayers at room temperature revealed even faster electron scattering fromKtoQvalley,[83]mostly because of the enhanced electron-phonon scatterings at elevated temperature.Similar to molecular orbital tomography, by Fourier transforming the momentum space exciton signal, one obtains the real space exciton wave function that has a radius of~1.4 nm, agreeing well with the literature,except that the substrate screening may cause slight modification of the radius.[403]Observations in bulk measurements showed slightly larger exciton radius,which can be attributed to reduced screening in the bulk form.[84]We note that under quasi-equilibrium conditions, when the inter-exciton distance is larger than the intrinsic exciton wavelength,the intrinsic exciton dispersion follows that of the VBM.[373]
Besides the intrinsic excitons in monolayer TMDs, exotic excitonic species can be created in TMD heterostructures by stacking two monolayers under the condition of type-II band alignment.In this case, the electron and hole are separated,and reside in different layers,respectively,forming the so-called interlayer exciton.[404]Because of the charge separation, the interlayer exciton has orders of magnitude longer lifetime, at a cost of exciton oscillator strength.Interestingly, when a small twist angle exists between the monolayers in forming the heterostructure, a new potential landscape can be induced via the moir´e superlattice.Consequently,excitons can be localized by such artificial moir´e potential landscape,[405-408]inducing strong correlation physics that is absent in natural TMDs.[409]Therefore, it is of great interest to understand the formation,evolution and recombination dynamics of these intricate excitonic species in both real and reciprocal spaces.
Using the same TR-MM setup, Karniet al.[88]first reported the photoemission signatures of the interlayer excitons in MoS2/WSe2heterostructures.The demonstration was based on the observations of both electron and hole dynamics, as well as the exciton center of mass momentum, in the 2.2±0.8°twisted MoS2/WSe2heterostructure.The direct visualization of the moir´e electron distribution in momentum space, i.e., electronic structures in the moir´e mini-Brillouin zone,however,is still lacking.
Direct evidence of moir´e excitons in momentum space was reported by Schmittet al.in MoS2/WSe2heterostructure,but with a twist angle of 9.8°±0.8°.[86]The large twist angle suppresses the center-of-mass effect of the interlayer exciton,and provides a larger mini Brillouin zone due to the smaller moir´e unit cell, allowing clear separation of the moir´e exciton distributions.Here, the pump pulse energy can be tuned from 1.7 eV to 2.4 eV, and with a pulse duration of~50 fs.The probe EUV pulse is generated by performing HHG of the 515 nm pulse, which features an energy~26.5 eV and pulse duration of 21 fs.The MM instrument is based on the ToF-MM.Figures 13(a)-13(c)show the full momentum space imaging of the single particle spectra of the A exciton,Σ dark exciton and moir´e excitons in the heterostructure sample, respectively,at selected time delays.The lower panel shows the zoom-in images of the corresponding excitonic species within specific momentum regions of interest.The hexagonal Brillouin zones of the monolayers and the moir´e mini zone structure are also overlaid.Clearly, while the momentum distribution of the intralayer A and Σ excitons resemble the wellknown hexagonal distributions, the interlayer moir´e excitons show additional three-fold symmetric distribution around the MoS2K-point.Such observation is rather intriguing because one would expect the moir´e landscape can spatially modulate all excitonic species.To clarify the origin of the extra momentum structure of interlayer excitons,it is worth noting that the exciton center of mass broadening, reported by Karniet al.,[88]is not observed in heterostructure with large twist angle.This indicates that the exciton wave function is spread over more than one moir´e unit cell, in contrast to the exciton localization effect that induces strong exciton correlation.In addition,the fact that the three-fold modulation is only present for interlayer exciton rules out the electron final state effect in the photoemission process, as it would imprint similar structures to all other species.Moreover,because the moir´e structure of the observed photoelectrons can be well reproduced by an electron Umklapp process,[410]it is thus expected that the Umklapp process can be transferred to the hole after electron being ionized.Therefore, it is essential for the electron and the hole of an exciton to reside in different layers, such that both lattice periodicities can be experienced by the exciton.In fact, the three-fold photoemission spots are nicely located at the corners (κpoints) of the moir´e mini-Brillouin zones,demonstrating these additional momentum structures of interlayer excitons to be associated with the moir´e potential landscape.
Finally,via Fourier analysis,it allows the extraction of the real space imaging of the interlayer excitons modulated by the moir´e superlattice, which has an exciton radius of~1.6 nm[Fig.13(d)].Although the size of the moir´e cell is~1.8 nm,the moir´e exciton wavefunction has a broad spatial spread that extends over one moir´e unit cell,indicating the interlayer excitons are not confined by the moir´e landscape.In contrast,Fig.13(e)also shows the real space wavefunction distribution of the intralayer A exciton.Clearly, it is much smaller than that of the interlayer exciton,showing that the coulomb force is reduced when forming the interlayer exciton.
Fig.13.Ultrafast momentum microscopy imaging of moir´e excitons in the MoS2/WSe2 heterostructure.(a)-(c) TR-MM imaging of intralayer bright A exciton, Σ dark exciton, and interlayer moir´e excitons, respectively.The corresponding constant energy and time delay are labeled in the top panel.The bottom panel gives the zoom-in image of the regions enclosed by the dashed circle.The intrinsic and the moir´e mini Brillouin zones are also plotted.The moir´e excitons are featured by the three-fold photoelectron distribution that coincides with the corners(κ points)of the mini Brillouin zone shown in(c).(d)and (e) Extracted real space wavefunctions of the interlayer and intralayer A excitons.Their corresponding momentum space images are shown as insets.Clearly,the interlayer exciton has much larger spatial spread,resulting in reduced Coulomb screening.All panels adapted with permission from Ref.[86].
Along the line of studies of excitons in TMDs, further reports on the dark-field real space imaging of moir´e excitons, electron-hole correlations in interlayer excitons,were reported.[32,376]Excitingly,there remains a large amount of interesting problems waiting to be explored by TRMM, and also TR-PEEM.For example, with the development of heterostructure engineering of layered materials(graphene, TMDs, etc.), one is allowed to look into more exotic physics, including twist-induced ferroelectricity,[334-336]correlated excitonic states,[392,411]and others, to unravel how quasiparticle, and many-body interactions take place in the presence of spatially modulated potential landscapes.Moreover, beyond layered materials, copper, iron, and nikel based superconductors,[412]kagome materials with spin frustrations,[413]in the bulk or thin film forms are also of great interest in TR-MM/PEEM studies.Because they can potentially demonstrate how competing quantum phases of matter, such as superconductivity and charge density waves,are formed or destroyed,with superior spatiotemporal resolution.Therefore,one can envision the spatiotemporal probe of a broad scope of physics with nano-femto resolutions could revolutionize our understanding of the excited states in manybody physics on the quantum scale.
5.Summary&perspective
In this review, we surveyed several major, and rapidly growing research directions carried out using TR-PEEM and TR-MM.Regarding the TR-PEEM imaging,the material systems that have been extensively investigated in the literature mostly belong to metallic systems with strong photoemission signals, such as plasmonic materials, where the photon energies of the illumination light sources mostly reside in the near infrared to visible to ultraviolet regime.While steady state and ultrafast properties of plasmons have been studied for decades, the employment of ultrafast lasers nevertheless showed exotic physics on the nano-femto scales, including plasmon-plasmon coupling,[59,210,213,214,217]plasmonic vortices,[55,261,263,268]plasmonic spin-orbit angular momentum conversion,[58]and plasmonic field and spin topological quasiparticles.[14,15,61,262]In addition, because of the strong field enhancement, the application of these nano plasmonic sources for strongly nonlinear light-matter interactions is also emerging.[62,414]More interestingly,the blossom of 2D materials has opened a large variety of plasmonic, and in general,polaritonic materials,[415-417]including metallic graphene,semiconducting black phosphorus,and even insulating h-BN,or a combination of these systems.While some of these have been reported in steady state PEEM measurements,[169,418-420]the capability in resolving related polariton physics in the time domain will provide deeper understanding of the quasiparticle and many-body interactions in these layered materials.
Beyond photonic/polaritonic modes, real space imaging of the electronic properties enabled by TR-PEEM can be further employed to low-dimensional quantum materials.For example,topologically protected surface and edge states are expected to show enhanced density of states at the Fermi level of the supporting materials, and thus it is expected to see these quasiparticles in real space using surface sensitive TRPEEM.[24,421-425]Therefore, the creation, propagation, and annihilation of quasiparticles in these topological states,which reflect the dynamical properties of quantum spin Hall effect or quantum anomalous Hall effect,[426,427]may be revealed.What’s more, material systems hosting strong electron correlations are also of great interest for TR-PEEM imaging.It is known that the superconducting channels in high temperature superconductors, as well as the charge density wave and antiferromagnetic order distributions, are inhomogeneous in space.[321,322,428]It is thus of importance to have the capability to resolve these electronic properties with nano-femto resolutions,to gain insight into the local electronic properties on the scale that can bridge the resolution of optical microscopies and scanning tunnelling electron microscopy or transmission electron microscopy.
On the spectroscopic side,TR-MM,equipped with PEEM objective lens and EUV probe light,has significantly advanced the understanding of carrier and exciton physics in graphene,TMDs and others.[43]With the matureness of the TR-MM instrument, for example incorporating liquid helium sample temperature and electron spin detection, a large amount of exciting physics problems,[18,20,21,24,424,425,429,430]including many-body excitations in TMDs, strongly correlated electronic states in superconductors and antiferromagnets, topological edge and surface states physics in topological materials, as well as non-equilibrium phases of matter, are thus awaiting to be explored.In fact,some of these problems are already being attempted with state-of-the-art (TR-)MM/PEEM methods.[10,33,431]While the ultimate energy and momentum resolutions may be limited by the PEEM objective lens due to the uncertainty principle, it certainly shows excellent performance in studying micron sized samples with superior imaging efficiency.
One challenge in better resolving electronic structures in the momentum space is the number of photoelectrons collected, and thus the signal to noise ratio, of one measurement.Currently, a reasonable time-series measurements may take tens of hours to a few days, depending on the laser repetition rate and temporal sampling points.It is therefore urgent to develop light sources,especially EUV probe pulses,of high brightness, high repetition rate, and tunable photon energy and polarization states.More interestingly,because EUV pulses are essentially attosecond pulse trains, it is therefore critical to mature the technique to generate isolated attosceond pulse, to push the limiting temporal resolution down to subfemtosecond.[192,193]While these techniques have been mostly applied in the atomic or molecular systems,their implementation to TR-PEEM/MM will certainly embrace exciting problems and bring new challenges.
Ultimately, one could expect TR-PEEM/TR-MM will assist the understanding of more excited states physics in condensed matter materials in a multidimensional parameter space,with superior time,energy,space,momentum,and spin resolutions that can hardly be achieved by other techniques.
Acknowledgements
Project supported by the National Natural Science Foundation of China(Grant No.12374223)and Shenzhen Science and Technology Program(Grant No.20231117151322001).
- Chinese Physics B的其它文章
- A multilayer network diffusion-based model for reviewer recommendation
- Speed limit effect during lane change in a two-lane lattice model under V2X environment
- Dynamics of information diffusion and disease transmission in time-varying multiplex networks with asymmetric activity levels
- Modeling the performance of perovskite solar cells with inserting porous insulating alumina nanoplates
- Logical stochastic resonance in a cross-bifurcation non-smooth system
- Experimental investigation of omnidirectional multiphysics bilayer invisibility cloak with anisotropic geometry

