On the generation of high-quality Nyquist pulses in mode-locked fiber lasers
Yuxuan Ren(任俞宣), Jinman Ge(葛锦蔓), Xiaojun Li(李小军),Junsong Peng(彭俊松), and Heping Zeng(曾和平)
1State Key Laboratory of Precision Spectroscopy,East China Normal University,Shanghai 200062,China
2National Key Laboratory of Science and Technology on Space Microwave,China Aerospace Science and Technology,Xi’an 710100,China
3Chongqing Key Laboratory of Precision Optics,Chongqing Institute of East China Normal University,Chongqing 401120,China
4Jinan Institute of Quantum Technology,Jinan 250101,China
Keywords: mode locking,laser,soliton,fiber,pulse
1.Introduction
A Nyquist pulse is a kind of signal source that satisfies the Nyquist criterion[1]due to its zero intersymbol interference.Due to the rectangular-shaped spectrum and sinc-shaped temporal waveform, Nyquist pulses have high value in modern communication technology, from electronic communications to optical communications and ultrafast science.For example, in the field of optical communications,[2-15]Nyquist pulses can increase the bandwidth of the systems.[16]Various studies on Nyquist pulses have been reported.[17-21]Near-ideal Nyquist pulses can be generated by electrical methods with the help of an arbitrary waveform generator.[22]Due to its unmatched performance, passive mode-locking technology has developed rapidly over the past few decades.[23-26]Nyquist pulses can also be generated in passively mode-locked fiber lasers by spectral filtering effects.[19]A passively mode-locked fiber laser is a dissipative system composed of nonlinearity,dispersion, loss, gain, and a saturable absorber effect;[27]all these effects are crucial to pulse shaping in the laser.An excellent work revealed that Nyquist pulse shaping can be affected by the bandwidth and shape of the spectral filter.[19]However,it is still elusive whether other effects affect Nyquist pulse shaping in mode-locked lasers.
In this work,we demonstrate that the quality of a Nyquist pulse can be significantly affected by the dispersion, linear losses and gain in mode-locked fiber lasers.We also discover that the ideal Nyquist pulse experiences a state transition during intracavity evolution.A similariton is generated in the erbium-doped fiber(EDF)segment,and it changes into an ideal Nyquist pulse after passing the rest of the cavity.
2.Numerical modeling
A Nyquist pulse in the time domain is written as follows:
whereτpis the pulse duration between zero crossings,andβis called the roll-off factor and has values in the range of 0 to 1.The sine-shaped Nyquist pulse(β=0)is an ideal pulse source due to its rectangular spectrum and zero roll-off.
Figure 1(a) depicts a schematic of the passively modelocked fiber laser.The 1.5-m erbium-doped fiber(EDF)is the gain medium;an isolator(ISO)is employed for unidirectional operation, and a spectral filter (SF) is used for Nyquist pulse shaping.The pump power is coupled into the cavity through a wavelength division multiplexer (WDM), and the signal is coupled out using an output coupler (OC).Mode locking is realized by a nonlinear polarization rotation(NPR)device.
To give an accurate description of the pulse propagation in the cavity, we utilize the discrete model of the nonlinear Schr¨odinger equation(NLSE)[28]
whereU(z,t) represents the slowly varying amplitude of the pulse envelope, which is the function of the propagation distancezand timet;β2is group velocity dispersion(GVD).We takeβ2=65 ps2·km-1and-22.5 ps2·km-1for the EDF and the SMF,respectively;γis a nonlinear coefficient,and we takeγ=8 W-1·km-1andγ=1.5 W-1·km-1for the EDF and the SMF,respectively;Ωg=50 nm corresponds to the full width at half maximum (FWHM) of the gain profile;gdenotes the small signal gain of the EDF,which can be expressed as wherePis instantaneous pulse power;Psatis the saturation power;qandqsatare the modulation depth and the unsaturable loss,respectively.

In the cavity,the SF plays a spectral shaping role,which is crucial for Nyquist pulse shaping.After filtering,the spectrum of the amplified pulse has two sharply decreasing edges and a tunable top,which is given by
In Eq.(5), Δωdenotes the filter bandwidth;α >0 (α <0)yields a convex (concave) Gaussian top, whose curvature is defined by the absolute value ofα.Asα=0, the SF can be regarded as a gate function.

Fig.1.(a) A schematic of the simulated fiber ring-cavity laser.(b) The governing law of the Nyquist pulse generation in the laser.
3.Simulation results and analysis
A split-step Fourier method has been employed as a numerical model.[29]The simulation starts from an initial chirpfree Gaussian pulse with a pulse width of 1 ps and peak power of 100 W centered at 1550 nm.By carefully setting the parameters,a stable sinc(β ≈0)Nyquist pulse train can be generated after about 3000 roundtrips, as shown in Fig.2.Specifically,we setPsat=28 W,Esat=65 pJ,and fix both parameters of the modulation depth and unsaturable loss at 0.2.A linear loss of 0.44 is considered.In addition,the net dispersion of the laser is 0.077 ps2, which is realized by setting the SMF length at 0.9 m.The SF’s bandwidth is 7 THz(Δλ ≈9 nm),andα=0(Eq.(5)).

Fig.2.Characteristics of the output Nyquist pulse in the time domain(a)and frequency domain(b).
3.1.Effects of net dispersion
Firstly,we fix the other parameters,and change the length of the SMF to investigate how the intracavity dispersion affects the properties of the generated Nyquist pulse.The simulation results are shown in Fig.3.As we can see,together with the decrease in the fiber length from 2 m to 0.4 m, the intracavity dispersion rises up from 0.053 ps2to 0.089 ps2,which slightly enhances the bottom oscillation of the Nyquist pulse[Figs.3(a),3(c)and 3(e)].Moreover,with the increase in the total dispersion,there is an interesting phenomenon observed,where the top of the Nyquist pulse spectrum goes through a transformation from the “convex top” to the “concave top”[Figs.3(b) and 3(f)].Notably, in the process of the transformation, we are able to achieve a nearly sinc-shaped Nyquist pulse by controlling the fiber length, as shown in Fig.3(d).The temporal waveform gradually approaches the ideal sinc function as the corresponding spectrums are close to flat-top.
To describe the deviation of the output pulses from the ideal Nyquist pulse,we introduce the misfit parameterM,[19]
whereψis the waveform of the output pulse; andχrepresents the ideal Nyquist pulse.We calculate the misfit parameter between numerical spectrums and standard rectangular fits.Here,M=0.0016 for net dispersion of 0.0525 ps2,M=0.0022 for net dispersion of 0.0885 ps2, andM=8.5×10-4for net dispersion of 0.07725 ps2,which means the simulation is in good agreement with the theoretical fit.
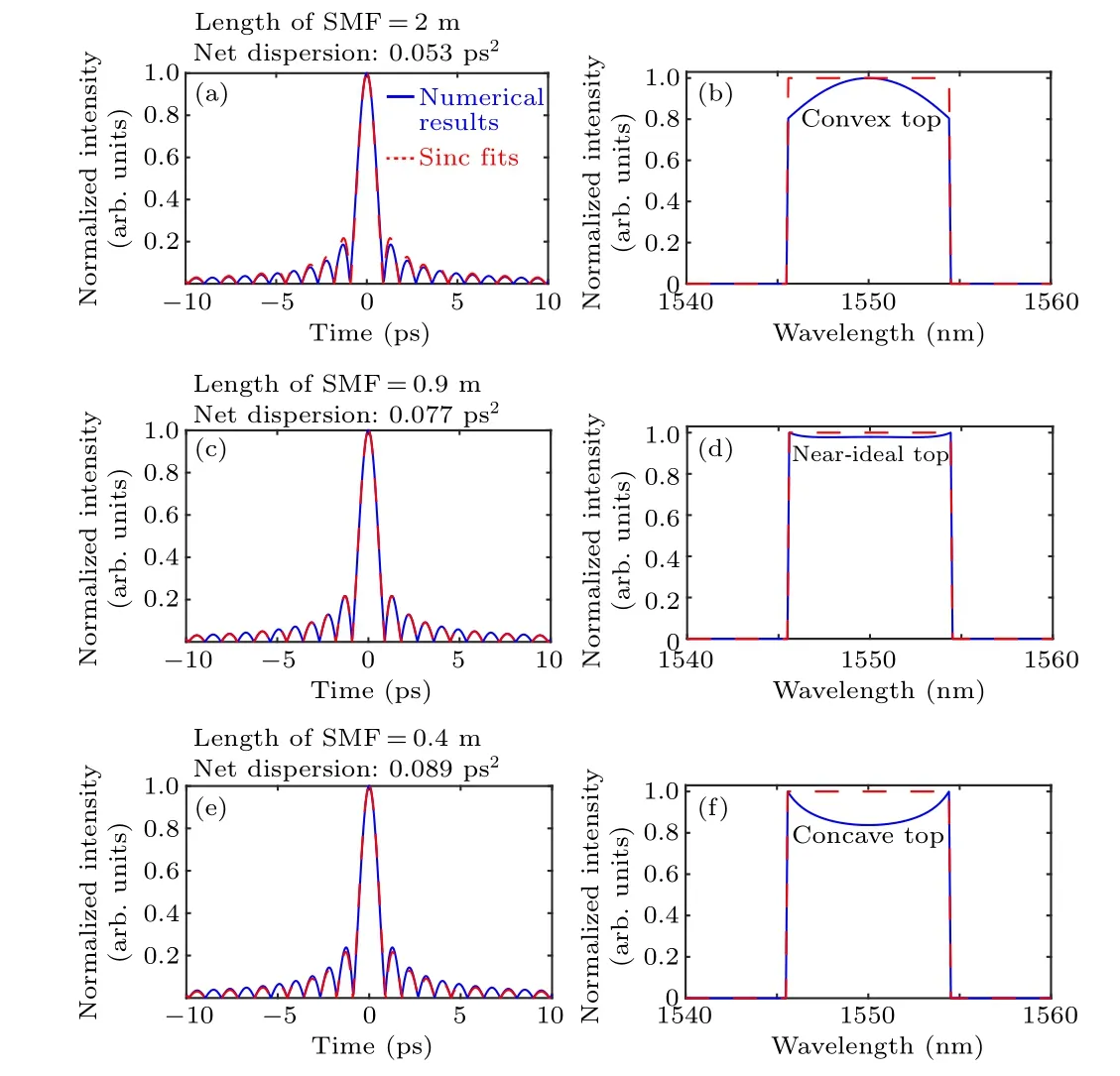
Fig.3.Blue solid line: the temporal (left side) and spectral (right side)profiles of the Nyquist pulse generated under different intracavity dispersion.Red dotted line: the sinc-shaped Nyquist pulse (β =0).[(a) and(b)] The 2-m SMF corresponds to intracavity dispersion of 0.053 ps2.[(c) and (d)] The 0.9-m SMF corresponds to intracavity dispersion of 0.077 ps2.[(e) and (f)] The 0.4-m SMF corresponds to intracavity dispersion of 0.089 ps2.
3.2.Effects of cavity linear loss and gain
We also study the effects of the linear loss on the output Nyquist pulse.In the calculation, we choose three different coupling ratios of the OC(0.42,0.48 and 0.54)to control the loss.The other parameters are the same as those used in Fig.2.The results are shown in Fig.4.With the increase in the intracavity loss,in the spectrum domain,a convex top shows up and has a gradually growing curvature.The misfit parameterM=0.0013,M=9.81×10-4andM=6.371×10-4in Fig.3(b),3(d),and 3(f),respectively.
We also demonstrate the effects of the pump energy.The gain saturation energy is adjusted from 50 pJ to 75 pJ, and a similar variation trend is found as before.As shown in Fig.5,a concave top spectrum is obtained underEsat=50 pJ; with the growth ofEsat,the top of the spectrum gradually curves in the opposite direction against the effects of linear loss.

Fig.4.Blue solid line: the temporal (left side) and spectral (right side)profiles of the Nyquist pulse generated under different linear losses.Red dotted line: the ideal Nyquist pulse.[(a)and(b)]Linear loss=0.42.[(c)and(d)]Linear loss=0.48.[(e)and(f)]Linear loss=0.54.

Fig.5.Blue solid line: the temporal (left side) and spectral (right side)profiles of the Nyquist pulse generated under different Esat.Red dotted line: the ideal Nyquist pulse.[(a) and (b)] Esat =50 pJ.[(c) and (d)]Esat=65 pJ.[(e)and(f)]Esat=75 pJ.
4.Similariton shaping in the Nyquist pulse laser
It has been reported that a pulse can be transformed to be a similariton[30-35]in the gain medium with normal dispersion due to the nonlinear attractor effect.[36]We also find that the Nyquist pulse becomes a similariton during the propagation in the EDF.Figure 6(a)shows the temporal evolution of the initial pulse in one roundtrip.As we can see, after the OC, we can obtain a near-ideal Nyquist pulse,as shown in Fig.6(c).
However, the pulse in the cavity does not evolve into a Nyquist pulse directly, but undergoes a similariton shaping process in the EDF due to the above-mentioned nonlinear attractor effect, as shown in Fig.6(b).For a clear comparison, pulse waveforms after the EDF and OC are fitted via a parabolic function as a red dotted line, and a sinc function as a black dotted line, as shown in Figs.6(b) and 6(c).It is apparent that the pulse passing through the EDF is close to being parabolic, and far away from the sinc function.By contrast,the output Nyquist pulse does not have a parabola shape.

Fig.6.Temporal evolution(a)of a pulse in one roundtrip.(b)The pulse waveform in the EDF.(c) The output Nyquist pulse: the red dotted line denotes parabolic fits,and the black dotted line is sinc-function fits.
5.Conclusion
In summary,we have numerically investigated the condition of the Nyquist pulse generation in a fiber ring-cavity laser.We find that the quality of Nyquist pulses depends on four effects: gain, dispersion, linear loss and spectral shaping.We also show that Nyquist pulses suffer from similariton shaping in the gain medium due to the nonlinear attractor effect.
Acknowledgments
Project supported by the National Natural Science Foundation of China (Grant Nos.11621404, 11561121003,11727812, 61775059, 12074122, 62022033, and 11704123),Shanghai Rising-Star Program, the Sustainedly Supported Foundation by the National Key Laboratory of Science and Technology on Space Microwave (Grant No.HTKT2022KL504008), Shanghai Natural Science Foundation(Grant No.23ZR1419000),and the National Key Laboratory Foundation of China(Grant No.6142411196307).
- Chinese Physics B的其它文章
- A multilayer network diffusion-based model for reviewer recommendation
- Speed limit effect during lane change in a two-lane lattice model under V2X environment
- Dynamics of information diffusion and disease transmission in time-varying multiplex networks with asymmetric activity levels
- Modeling the performance of perovskite solar cells with inserting porous insulating alumina nanoplates
- Logical stochastic resonance in a cross-bifurcation non-smooth system
- Experimental investigation of omnidirectional multiphysics bilayer invisibility cloak with anisotropic geometry

