路基边坡预应力锚索抗滑桩支挡结构受力特性和抗震效果有限元分析

吴育科

（中电建（丽水）规划勘测设计研究院有限公司，浙江 丽水 323000）

0 引言

路基边坡治理是公路建设中的一大难点，选择合理的路基边坡支护方式可有效保障边坡稳定[1-3]。预应力锚索抗滑桩作为一种锚索和桩的组合支挡结构，可通过二者合作共同受力来抵抗滑坡推力，从而实现一般抗滑桩的被动抗滑向主动抗滑的转换。这种抗滑桩支挡结构在路基边坡加固中应用较为广泛[4,5]，用好与否关系到路基边坡的稳定性和抗震性能。本文利用MIDAS/GTS岩土有限元软件模拟分析不同强度折减系数下抗滑桩和锚索的受力特性，以及地震作用下预应力锚索抗滑桩支挡结构应用效果。

1 工程概况

某路基边坡地处灾害频发地带、岩体破碎，由于地质构造运动剧烈，边坡存在明显位移。边坡总体呈扇形，主轴长约75m。顶端、下缘宽度分别为45m，150m。边坡区呈现山前斜坡地貌。坡度和坡高分别约为20°、25m，滑坡后缘结构较为清晰。边坡地层由下至上分别为：粉砂质页岩层、风化泥质页岩层、含碎石粉质黏土层，平均厚度均约为10~15m。边坡岩土参数见表1。

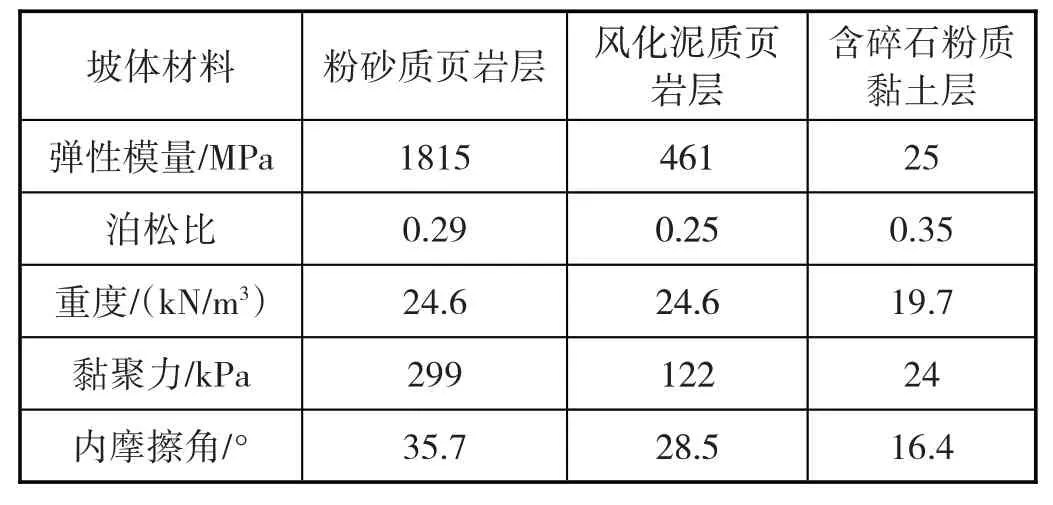
表1 边坡岩土参数

2 预应力锚索抗滑桩支挡结构方案

为避免研究区边坡产生大面积失稳引发滑坡，采用预应力锚索抗滑桩支挡结构进行治理，应用C30混凝土完成预应力锚索抗滑桩浇筑，容重取值为25kN/m3；桩总长、受荷段、嵌固段长度分别为13m、7m、6m；锚索长度及弹性模量大小分别为11.5m、200MPa；锚索与水平地面间的夹角为10°，同时为锚索施加的预应力大小为100kN。预应力锚索抗滑桩支挡结构其他设计参数见表2所示，支护布置方案如图1所示。

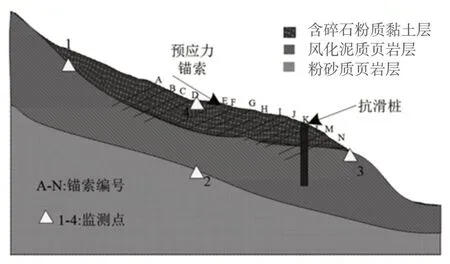
图1 支护布置方案

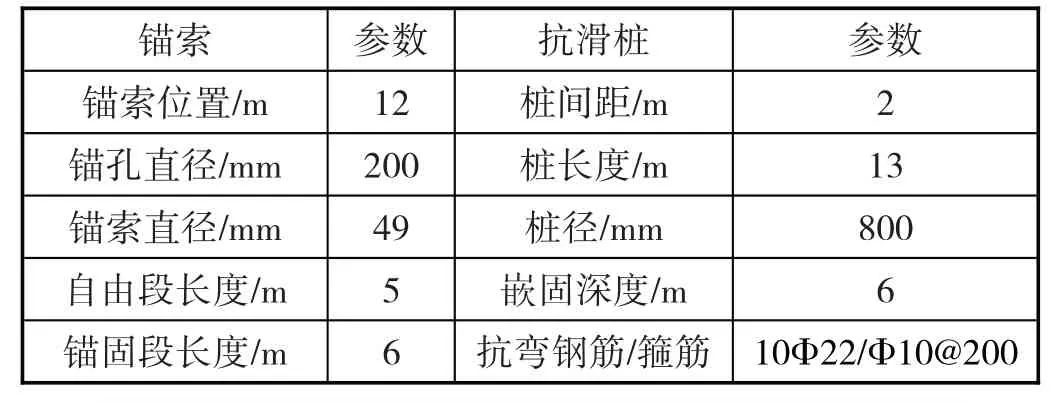
表2 预应力锚索抗滑桩支挡结构设计参数

3 预应力锚索抗滑桩支挡结构力学计算模型

预应力锚索抗滑桩支挡结构中，锚索与桩分别作为主动与被动支挡结构。桩支护完成后，通过锚索固定于边坡的稳定地层中，通过组合锚索与桩共同对抗边坡的推力。具体的预应力锚索抗滑桩加固边坡的力学示意图如图2所示。

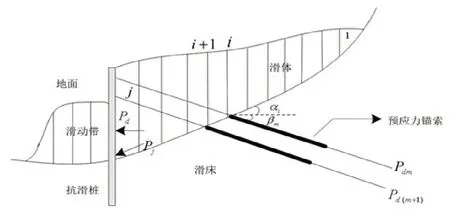
图2 预应力锚索抗滑桩加固边坡的力学示意图

当锚索与桩共同对抗边坡的推力时，若边坡不稳固产生的推力首先由锚索来抵抗，由桩承担的边坡推力便减小，此时锚索所抵抗的边坡推力为F，锚索预先替桩承担的边坡推力便为F传递至桩位置处的水平推力Pdm。因此，桩实际抵抗的边坡水平推力值Pd的计算方式为：未考虑锚索抵抗边坡推力条件下设桩位置所承担的边坡推力设计值PT与锚索预先替桩承担的边坡推力Pdm之间的差值，即：Pd=PT -Pdm。详细分析如下：

用N描述边坡由上至下所划分的条块数量，穿过边坡滑面的预力锚索m处于条块i的位置，条块j的位置为设桩位置。桩所抵抗的边坡水平推力设计值Pd的计算公式

式中：λ、λk、K——分别为边坡岩性折减系数及推力传递系数、工程设计安全系数；

Pm、Pj——分别为第m条锚索的设计拉力值、桩的位置承担的边坡推力，且Pj⋅cosαj=PT；

αj、βm——分别为桩所处滑面的倾角、第m条锚索的倾角；

αi、φi——分别为边坡滑块i位置处的倾角、内摩擦角。

通过加入锚索折减系数ηm理念，便于预应力锚索抗滑桩加固边坡的力学计算，ηm用于描述预应力锚索抗滑桩共同进行加固边坡时，锚索拉力传递至桩所在位置时，锚索实际抵抗边坡水平作用力除以锚索拉力值Pm的结果，计算表达式如下：

锚索与桩的协调表达式为：

则公式（1）的简化结果表达式为：

锚索预应力值和拉力值求解过程如下：依据边坡推力设计值，设定锚索拉力值，并依据公式（4）计算桩所处位置所受边坡推力设计值。遵循公式（3）完成通过锚索协调后的变形拉力值求解，锚索预应力值大小即为：锚索拉力值与通过锚索协调后变形拉力值的差值。

预应力锚索抗滑桩支挡结构力学计算模型，结合了锚索和桩的协调受力，一起抵抗边坡推力，锚索既可以承担部分边坡滑力，还对桩施加了拉力，完成边坡加固的同时限制桩身的变形。

4 数值模拟模型

采用在边坡支护工程数值模拟中应用较为广泛的MIDAS/GTS岩土有限元软件进行本文边坡防护中的预应力锚索抗滑桩支挡结构数值模拟，预应力锚索抗滑桩支挡结构三维模型如图3所示。土体、抗滑桩及预应力锚索分别应用莫尔库伦本构模型、3D弹性实体单元以及MIDAS/GTS中的植入式桁架单元完成模拟，边坡坡面和护坡均使用壳单元进行模拟；边界和四周分别采用固定及自由场边界。

图3 预应力锚索抗滑桩支挡结构三维模型

5 抗滑桩支挡结构边坡防护技术及效果分析

5.1 抗滑桩受力特性分析

应用MIDAS/GTS岩土有限元软件分析不同强度折减系数下（1.0、1.1、1.2）抗滑桩的内力变化，结果如图4所示。

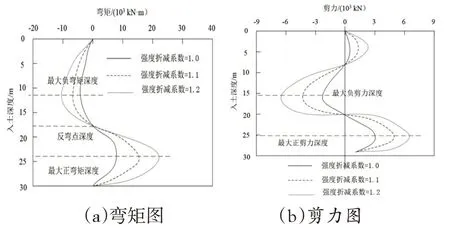
图4 不同强度折减系数下抗滑桩的内力变化

分析图4（a）可知不同强度折减系数下抗滑桩弯矩变化情况。抗滑桩反弯点出现在入土深度为18m处，反弯点上、下两部分的弯矩值分别为负值和正值，代表这两部分的抗滑桩分别承受拉力和压力，最大拉力、压力对应图中最大负弯矩深度、最大正弯矩深度，分别为12m、24m。强度折减系数的增加不会改变弯矩的分布情况，但会增加弯矩值，同时负弯矩的增加幅度显著低于正弯矩增加幅度。当强度折减系数为1.0 时，加固边坡为工作状态，此时最大正、负弯矩分别为8.5×103kN·m、-4.5×103kN·m；当强度折减系数增加到1.2时，加固边坡已达到极限状态，此时最大正、负弯矩分别达到22.5×103kN·m、-10.5×103kN·m。

分析图4（b）可知不同强度折减系数下抗滑桩剪力变化情况，在抗滑桩入土深度分别为8m、20m两处时，抗滑桩的剪力为0，8~20m深度之间时，抗滑桩桩体剪力为负数，8~20m 深度之外，抗滑桩桩体剪力为正数。最大正、负剪力深度分别为25m、15.5m，随着强度折减系数的增加，剪力分布情况不变，但剪力值增加，当强度折减系数为1.0时，加固边坡处于工作状态，此时的最大正、负剪力值分别为3×103kN、-2.5×103kN；当强度折减系数增加至1.2时，加固边坡处于极限状态，此时的最大正、负剪力值分别为6.4×103kN、-6.5×103kN。

5.2 锚索受力分析

为分析预应力锚索抗滑桩支挡结构中各锚索的受力特性，统计不同折减系数下（1.0、1.1、1.2）图2 中编号A-N的锚索的内力变化情况，结果如图5所示。

图5 不同折减系数下锚索的内力变化情况

分析图5可知，整个边坡中，受牵引式滑坡影响，位于边坡下部的锚索最大轴力值高于边坡上部的锚索最大轴力值。相同折减系数下，E号锚索的轴力值最小，原因在于其位于边坡上部，此处坡体受推力较小，呈现较稳定态势；E号锚索的轴力值最大，其位于抗滑桩前端，受边坡推力较大。各个锚索的最大轴力值随着折减系数的增加逐渐增大，当折减系数为1.2时，此时边坡处于极限状态，滑动面下部剪出，导致编号为N 的锚索因轴力值达到锚固端极限拉拔值而失效拔出。

5.3 预应力锚索抗滑桩支挡结构方案的应用效果

为分析预应力锚索抗滑桩支挡结构方案的应用效果，从边坡中选取4个监测点，位置分别为：边坡上端1、2层岩土界面间（监测点1）、边坡中部2、3 层岩土界面间（监测点2）、边坡前端2、3 层岩土界面间（监测点3）、监测点2 上方的边坡表面处（监测点4），具体位置见图2。将4个监测点的位移时程曲线收敛性作为边坡失稳判断条件，模拟PGA=0.10g时Wolong地震波进行水平方向的50s激振作用下，预应力锚索抗滑桩支挡结构应用前后4个监测点的位移时程曲线，衡量支挡结构应用前后的边坡稳定性。结果如图6所示。分析图6可知，预应力锚索抗滑桩支挡结构应用前，随着地震波的持续作用，4个监测点的位移呈持续增加态势，其中监测点4地震作用下的位移最大，监测点2的位移最小，且地震波作用结束后，4个监测点的位移持续增加，说明边坡在地震波的持续作用下已经失稳。预应力锚索抗滑桩支挡结构应用后，随着地震波的持续作用，4个监测点的位移呈小幅度增加态势。与支挡结构应用前相同，还是监测点4在地震作用下的位移最大，监测点2的位移最小，说明地震作用下边坡表层的滑移最大，底层滑移相对较小，边坡上部的滑移相对边坡下部较大；在地震波作用结束后，4个监测点的位移不再继续增加，呈稳定态势，说明预应力锚索抗滑桩支挡结构应用后，边坡稳定性较好。

图6 抗滑桩支挡结构应用前后监测点的位移时程曲线

6 结束语

本文为提升路基边坡稳定性、增强其抗震性能，利用MIDAS/GTS岩土有限元软件模拟研究预应力锚索抗滑桩支挡结构在路基边坡防护应用中的受力特性和抗震效果。结果显示：强度折减系数的增加不会改变抗滑桩弯矩以及锚索剪力的分布情况，但会增加弯矩值以及剪力值，强度折减系数为1.0时，加固边坡为工作状态，强度折减系数为1.2时，加固边坡已达到极限状态；预应力锚索抗滑桩支挡结构的应用，可降低地震作用产生的位移，且地震波作用结束后，监测点位移不再继续增加，呈稳定态势，边坡稳定性较好。研究认为，预应力锚索抗滑桩支挡结构具备显著的路基边坡安全防护效果。