预应力混凝土桥梁锚下有效应力检测方法研究

文开荣

（四川路桥华东建设有限责任公司，四川 成都 610000）

0 引言

预应力钢束是预应力混凝土桥梁中非常重要的受力构件，其预应力度会影响整个预应力混凝土桥梁的使用安全[1]。但是由于预应力混凝土桥梁的张拉施工过程极其复杂、技术难度极大，并且工程管理人员和现场施工人员易出现管理不严、责任心较差的情况，致使预应力混凝土桥梁的实际有效预应力与标准值偏差较大，不符合相关质量控制指标[2]。因此，在预应力混凝土桥梁施工过程中，预应力检测是确保混凝土桥梁工程质量的重要措施。如果能够借助现场测试结果，并了解施工中锚夹具、拉张器以及其他辅助设备的现场状态，即可随时掌握预应力混凝土桥梁的施工质量控制情况，也能将预应力混凝土桥梁的施工质量控制水平通过全面、准确、科学的数字化形式体现出来，从而有效控制预应力混凝土桥梁的施工质量[3]。因此，对预应力混凝土桥梁锚下有效应力检测方法进行研究具有现实意义。

1 预应力混凝土桥梁锚下预应力的参数与分布特点

1.1 锚下预应力的技术参数

预应力混凝土桥梁锚下预应力的基本技术参数见表1。

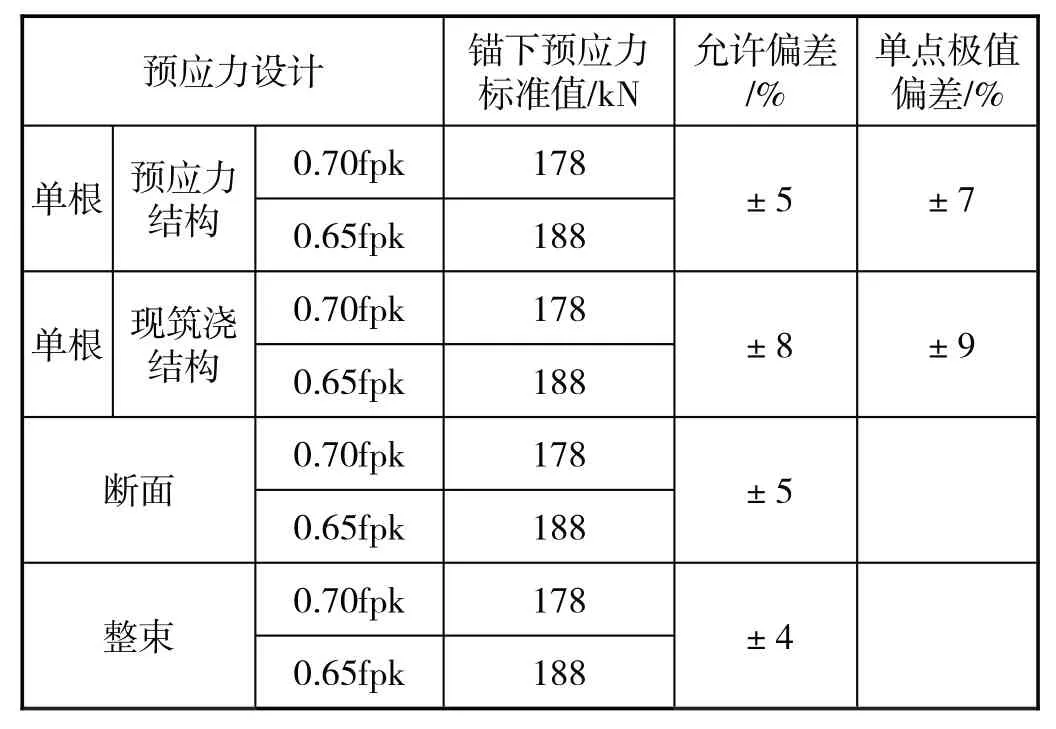
表1 预应力混凝土桥梁锚下预应力的基本技术参数

1.2 锚下预应力分布特点

在预应力混凝土桥梁中，预应力筋通常被布置在桥梁的受拉区域，通过张拉预应力筋并在锚固件处固定，从而在混凝土结构中产生预压应力。这种预压应力可以抵消桥梁在使用过程中由外部荷载引起的拉应力，从而提高桥梁的承载能力和抗裂性能。锚下预应力的分布特点主要包括以下几个方面：

（1）集中分布。预应力筋通常集中锚固在桥梁的关键部位，如梁端、跨中等位置。这些部位的预应力筋数量和锚固力较大，以确保在桥梁受到外部荷载时能够产生足够的预压应力。

（2）非均匀分布。由于桥梁结构的不均匀性和受力特点，锚下预应力在桥梁各部位的分布并不是均匀的。一般来说，受力较大的部位预应力分布较密集，而受力较小的部位则相对稀疏。

（3）空间分布。预应力筋在桥梁中的布置通常具有三维空间特性。根据桥梁的结构形式和受力需求，预应力筋可以在水平、垂直和斜向等多个方向上布置，形成复杂的预应力筋网。

（4）连续性与间断性。在某些情况下，预应力筋可能需要在桥梁的某些部位进行连续布置，而在其他部位则采取间断布置。这种连续性与间断性的布置方式可以根据桥梁的受力特点和施工条件进行灵活调整。

需要注意的是，锚下预应力的分布特点受到多种因素的影响，包括桥梁的结构形式、荷载特点、材料性能以及施工工艺等。因此，在实际工程中，需要根据具体情况进行详细的设计和计算，以确保预应力混凝土桥梁的安全性和耐久性。

2 基于多元线性回归函数的有效预应力检测原理及检测流程

2.1 锚下有效预应力检测原理

基于反拉法的锚下有效预应力检测的原理主要是通过测量预应力筋在反向拉力作用下的伸长量来推算锚下的有效预应力。这种方法利用“位移-力”曲线的检测原理，对孔道未注浆的预应力筋进行反向张拉，同时测量张拉力与预应力筋的伸长量。在反拉过程中，当反拉力小于锚下有效预应力时，夹片对预应力筋有紧固作用，预应力筋的伸长量主要来自于露出的自由长度部分。然而，当反拉力超过原有有效预应力时，锚头与夹片脱开，此时能够自由伸长的预应力筋除了露出的自由长度外，还包括一部分位于锚内的预应力筋。因此，预应力筋的总伸长量会有明显增加。同时，夹片本身也会随着预应力筋的伸长而产生向外的微小位移。通过精确测量反拉力与预应力筋或夹片的位移关系，可以绘制出“位移-力”曲线。根据这一曲线，可以推算出锚下的有效预应力值。这种方法具有测量精度高、操作安全简便、影响因素小等优点，被广泛应用于预应力混凝土结构的检测过程中。需要注意的是，反拉法检测应在预应力筋张拉施工完成后24h 内进行，且必须在未切割张拉预应力筋和孔道未压浆的情况下进行，以确保检测结果的准确性。此外，检测过程中应严格按照相关标准和规范进行操作，并由专业的检测人员进行实施。

2.2 锚下有效预应力检测流程

基于反拉法的锚下有效预应力检测的具体流程如下。

（1）接受委托任务后，进行资料收集和现场调查，以了解桥梁的基本情况和施工记录。

（2）根据调查结果，编制详细的检测方案。检测方案应包括工程概况、检测依据、检测内容、检测方法、检测仪器设备、所需的机械或人工配合、安全环保措施等。

（3）在检测前，对仪器设备进行检查调试，确保各项功能正常，为检测工作做好准备。

（4）在满足反拉法检测条件的情况下，即张拉施工完成后24h 内，未切割张拉预应力筋，孔道未压浆，进行反拉法检测。

采用反拉加载设备对预应力筋进行加载，同时利用力值与位移量测仪器实时记录加载过程中的张拉力和钢绞线或夹片的位移变化。按照预定的加载程序进行加载和卸载，即0→初应力（0.1σcon~0.2σcon）→反拉终止应力σp→0。在加载过程中，应控制加载速率，确保不超过规定的限值。在加载和卸载过程中，密切观察并记录预应力筋的应变响应。当达到反拉终止应力σp时，测量并记录此时的张拉力和钢绞线或夹片的位移量。根据监测数据，分析预应力筋的应变响应，反推出锚下有效预应力。通过与设计值进行比较，评估预应力筋的实际应力状态是否符合要求，以及是否存在预应力损失等问题。在整个检测过程中，应确保检测环境稳定，避免温度、冲击、振动、强磁场等干扰因素对检测结果的影响。最后，根据检测结果编制详细的检测报告，对锚下有效预应力状态进行评定，并提出相应的建议或措施。

3 基于多元线性回归函数的锚下预应力检测计算分析

当预应力混凝土桥梁的锚下有效预应力过大时，会出现钢绞线断丝的情况；当有效预应力过小时，易出现混凝土桥梁梁体横向开裂的情况[4]。由此可见，在实际施工中需有效控制预应力混凝土桥梁的锚下预应力数据，因此准确检测锚下有效预应力也是工作重点。在锚下有效预应力检测与预应力混凝土桥梁施工质量控制的过程中，可借助多元线性回归函数，其计算结果可为有效预应力检测提供理论与试验基础[5]。多元线性回归函数将预应力损失因素设为自变量，将预应力混凝土桥梁锚下有效预应力的试验值设为因变量，以此构建多元线性回归模型。

3.1 构建回归模型

将m个预应力损失因素设定为自变量X1,X2,…,Xm，由此构建m元线性回归模型，该回归模型Ya的具体公式为：

式中：U0,U1,…,Um——回归参数；

Xa,1,Xa,2,…,Xa,m——已知常数；

Xi—— 随机误差 ，其独立且服从 N(0,e2),i =1,…,n。

若已知常数项Xa,0= 1，那么m元线性回归方程为：

m元线性回归模型的矩阵具体如式（3）所示：

预应力钢筋和管道壁之间的摩擦σl1、锚夹具受压变形导致的损失σl2、预应力钢筋的应力松弛σl3等因素会影响预应力混凝土桥梁锚下有效预应力P的大小。由此可构建以下多元线性回归模型，具体公式如下：

式中：σl1a、σl2a、σl3a——自变量预应力损失因素；

Zpa——因变量预应力混凝土桥梁锚下有效预应力试验值；

X1a——随机误差，其独立且服从N( )0,e2,i =1,…,n；

σl1a、σl2a、σl3a——数值可通过现场实际检验数据获得。

3.2 最小二乘估计及相关性检验

多元线性回归模型的回归参数为Upb(b= 0,1,2,5)，运用最小二乘法估计Upb，假设X为m，那么回归平面度的残差平方和为：

若使eTe= min，那么U的最小二乘估计即为U∧，将式（5）进行求导并使其结果为0，即可获得：

将X，Y，U代入至式（6）中，即可获得回归参数的最小二乘估计，具体如式（7）所示：

综上可知预应力混凝土桥梁锚下有效预应力的多元线性回归方程为：

可以通过样本复相关系数R和服从自由度是(k,n-k- 1 )的F分布两个统计指标验证预应力混凝土桥梁锚下有效预应力回归模型的相关显著性，相关显著性越高说明通过函数计算的混凝土桥梁锚下有效预应力与现场实际测量的有效预应力更一致。其中，k为参变量个数，n为样本总数。

式中：相关系数R越接近1，那么相关性越显著。

4 锚下有效预应力的检测结果分析

对本文方法所构建多元线性回归模型进行相关性检验，试验获取30组现场实际检测数据，设定3个自变量，试验数据的自由度为（3,26），根据查F分布表，即可获得多元线性相关程度高达95%，且自由度为（3,26）的F值：F0.05()3,26 = 2.98，具体方差分析结果见表2，回归参数和多元线性相关性检验参数的计算结果见表3。

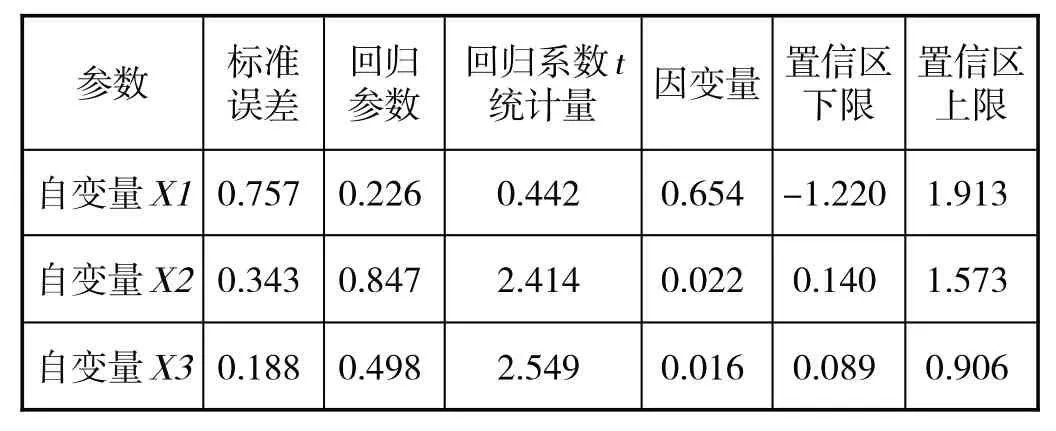
表2 方差分析结果

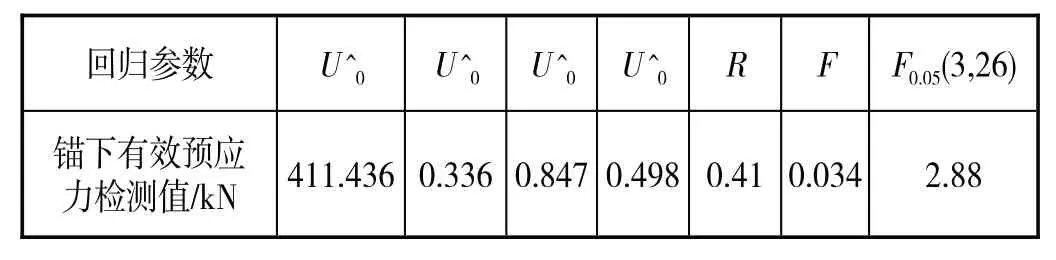
表3 回归参数和多元线性相关性检验参数的计算结果

在表2 中，回归系数t统计量是用来检验每个自变量对因变量的影响是否显著的。通常，如果t统计量的绝对值大于某个临界值（比如2），则可以认为该自变量对因变量有显著影响。在这里，X2 和X3 的t统计量远大于2，因此它们对因变量有显著影响，而X1的影响可能不太显著。置信区下限、上限表示回归参数的置信区间，由于置信区间不包含0，则可认为该自变量的影响是显著的。

在多元线性回归中，F统计量用于检验模型中至少一个自变量是否对因变量有显著影响。F统计量的值与模型中的自变量数量和残差自由度有关。由表3 可见，F的值为0.034，小于显著性水平0.05，因此本文方法所采用的回归方程回归效果较明显。

由上述分析可知，本文方法能够运用回归函数计算获得的混凝土桥梁锚下有效预应力和现场检测的有效预应力基本一致，说明本文方法能够对锚下有效预应力检测的结果进行准确预测，并为后续优化控制提供基础。

5 结束语

综上所述，及时有效地获得混凝土桥梁锚下预应力数据，并通过预应力对混凝土桥梁施工质量进行控制，是工程建设中的重要环节，也是工程进度需要密切关注的信息。本文方法能够较为准确地检测实际工作中混凝土桥梁锚下预应力，根据检测结果对混凝土桥梁进行调整，保证混凝土桥梁施工质量，提高混凝土桥梁预应力施工过程中的标准化程度。