工程塔式起重机械主动平衡分析及倾翻判定方法研究

马全静

（中铁十六局集团路桥工程有限公司，北京 密云 101500）

0 引言

塔式起重机是动臂装在高耸塔身上部的旋转起重机，由金属结构、工作机构和电气系统三部分组成，其工作范围大，主要用于多层和高层建筑施工中材料的垂直运输和构件安装。在塔式起重机具体操作过程中，可能会由于操作方式不合理导致塔式起重机发生倾翻事故，会对机械本身、人员安全、施工工期等造成不良影响。防止塔式起重机倾翻是工程项目建设需要重点关注的内容之一。基于此，开展工程塔式起重机械主动平衡分析及倾翻判定方法研究具有重要意义。

1 塔式起重机主动平衡分析及倾翻判定思路

1.1 主动平衡分析

塔式起重机主动平衡分析，就是在塔式起重机工作过程中，操控者要密切关注其作业姿态和工作方位，判断各支腿在塔式起重机不同作业状态下的受力程度，据此判断负载平衡状态，及时调控不平衡问题。根据塔式起重机运行特性设定临界倾翻判定条件，结合监测信息生成塔式起重机支腿合力的计算模型，进行Matlab仿真分析，识别可能引起塔式起重机倾翻的因素，为作业姿态调整、安全管控等工作提供指导。

1.2 倾翻判定

塔式起重机平衡重和压重的重量、形状和尺寸应符合吊装和固定的要求,并能承受规定的载荷不损坏。当平衡重和压重的重量偏小、安装位置不正确或未按要求予以可靠固定而发生位移时,塔式起重机稳定性将遭到破坏。塔式起重机各支撑臂的受力和4个支腿的受力数据是解决塔式起重机防倾翻技术问题的重要数据[1]。各项数据通过传感器检测而得，比如在4个支撑柱设置压力传感器和应变片，获取吊臂和旋转平台的受力信息；增设加速度传感器和陀螺仪，用于记录塔式起重机的运行信息，作为防倾翻控制依据；各项信息均被完整储存至黑匣子内，一旦发生塔式起重机倾翻事故，可追溯信息，探明事故的成因，采取更加有效的措施处理现场状况，并从中积累经验，进而不断优化塔式起重机作业方法和现场管理方法。

塔式起重机吊臂的变形及受力情况可通过压力传感器和力学传感器检测确定，从检测数据中识别危险因素，进行管控，以免发生安全事故。比如，传感器检测数据显示2个支撑柱的受力明显超过另外两边的受力时，表明塔式起重机负载失衡，可能发生倾翻事故，出于安全考虑，需要根据支撑柱的实际受力状态限制执行机构输出力矩。

2 塔式起重机平衡分析的数学模型

2.1 平衡分析简化模型

将塔式起重机平衡问题简化成数学模型，如图1所示。塔式起重机的负载发生变化后，支撑柱承载的压力有所改变，比如：在移动4个支撑腿的平板上的重物后，靠近重物的支撑腿受到的压力增强，达到一定程度就有倾覆的可能，且倾覆发生率将由于重物越靠近平板边缘而提高，只要重物越过2支撑柱2线处，一旦重物的质量明显超过平板质量，则极容易出现塔式起重机倾翻事故。

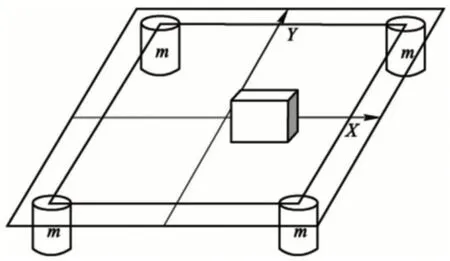
图1 平衡分析简化模型

图1中m为支撑柱质量，重物所在坐标位置为（x，y）。由于负载的变化特点的未知性，还需判断平板运动状态下物体的幅度响应和频率响应，其中尤为关键的是被吊重物的晃动幅度及频率，需要设定负载最大振幅Amax，最大振动频率Fmax。物体在中间位置时，塔式起重机整体稳定性最佳，物体向四周移动时，重心发生变化，塔式起重机的稳定性下降。

2.2 支腿合重心计算模型

车架-支腿体系的刚度大，支承面坚硬，因此使用过程中出现的相对变形量和相对沉陷量均较小，若总载荷合力不落在支腿外，则能够保证塔式起重机在起吊重物的工况下各支腿均与地面紧密接触，支撑状态稳定可靠，否则可能由于某个支腿离开地面而不受力，出现稳定性不足的三点支撑状态。

塔式起重机A、B、C、D四个支腿的受力俯瞰图，如图2所示。塔式起重机回转中心为O0，离支腿中心O的距离为e0，支腿间距为a、b。塔式起重机吊重时支承在四个支腿上，假定塔式起重机底盘不回转部分的质量为G2，重心在离支腿中心e2处，吊臂位置与塔式起重机纵轴线（x 轴）ϕ角。其中，e0、e2均带符号，定义为：在O 上侧为正，在O下侧为负。

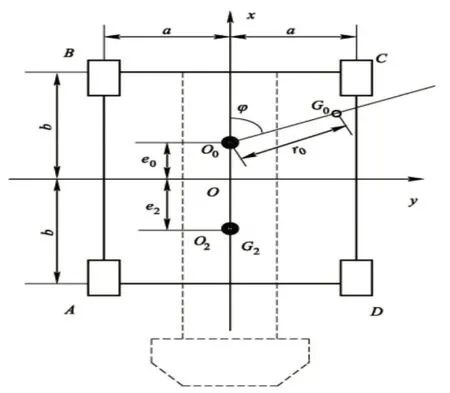
图2 塔式起重机支腿受力俯视图

根据图2以及如图3所示的塔式起重机支腿受力侧视图可知，作用在支腿的载荷包含吊臂平面内的力矩引起的力、上车回转部分合重力G0、底盘自重G2等，是多项力共同作用的结果。

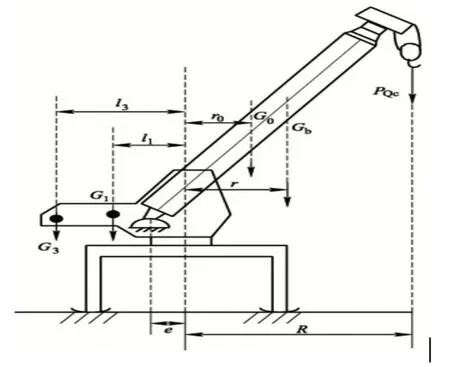
图3 塔式起重机支腿受力侧视图

合力G0为上车自重G1、吊臂自重Gb、配重自重G3、起升载荷重PQc的总和，关系式如下：

G0重心与O0的距离为：

式中：PQc——起升载荷重；

R——作业半径；

r——吊臂Gb到回转中心的距离；

l1、l3——分别为上车重心、配重G3重心到回转中心的距离；

G3——配重质量；

G1——上车自重。

在本项目中，根据载荷合力位置与支腿距离的反比分配支腿压力，此处分析中暂不考虑作用在吊臂头部作用的水平合力，比如回转惯性力、离心力等均不在本次分析的考虑范围内，则4个支腿的反力分别为：

整车重心根据上、下车重心和重力计算，方法如下：

整车合重心曲线公式：

3 塔式起重机倾翻条件判别的数学模型

3.1 安全域计算模型

根据前述有关负载平衡模型及塔式起重机合重心的分析，构建塔式起重机防倾翻安全域计算模型，即fmin＝（G，α，β），此模型基于相邻2支腿反力之和极限值构建。该模型可用于反映塔式起重机整车安全状况，式中G为塔式起重机的吊重，α和β分别为臂架运动的变幅角度、回转角度。

在明确塔式起重机工况时，如果塔式起重机臂长不发生变化，起重臂起升角度随着α变小而减小，并且以相邻2 支腿最小。在相邻2 支腿最小反力之和为0时，塔式起重机的稳定性急剧降低，可能出现倾翻现象。根据这一规律，设定相邻2 支腿最小反力之和的临界值，将其作为判断塔式起重机倾覆的关键依据，若达到临界值，则潜在隐患，随即启动报警，出于安全考虑，塔式起重机臂架停滞运动或反向运动，尽快使塔式起重机恢复平稳工作状态。再从塔式起重机4 支腿的分布位置来看，相邻支腿组合方式为支腿A 和B、支腿B 和C、支腿C 和D、支腿D 和A，共4 组，各组的合力分别定义为FAB、FBC、FCD、FDA，公式如下：

3.2 防倾翻的条件

根据前述提及的计算模型进行分析：相邻支腿压力之和达到最小值的情况发生在回转角为0°、90°、180°和270°时，应保证FAB、FBC、FCD和FDA均超过0，以此来避免塔式起重机倾翻现象，则必须满足如下要求：

在满足上述条件后，才更有利于保障塔式起重机吊装时的稳定性。若吊装半径不发生变化，则臂回转的角度将成为影响吊装安全的唯一因素，此影响特性与实际工程相符。塔式起重机保持安全运行状态时，可根据吊装需求做变幅运动，若设备运行状态稳定并且向幅长减小方向运动，则无需重新计算，可按照原参数运行即可。若塔式起重机向幅度变大方向操作，则需结合当前的运行状态进行计算与分析，判断是否具有安全性，若发现安全隐患将随即报警，经过管控后避免塔式起重机倾翻。

4 基于Matlab软件的仿真验证

相邻支腿压力之和随回转角度变化的曲线，如图4所示，此图形建立在变幅角度（幅度）一致的前提下，反映的是相邻2支腿压力之和的曲线。

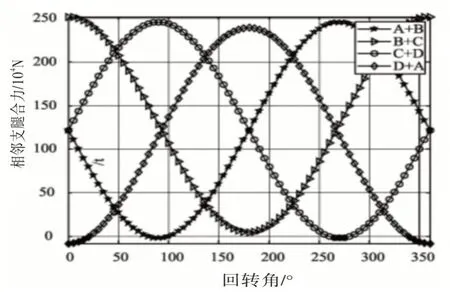
图4 相邻支腿合力与回转角的关系

幅长与吊臂平面内力矩关系，如图5所示。图5中的回转角度确定，随着幅长的增加，力矩随之增加，两者几乎具有线性变化关系。

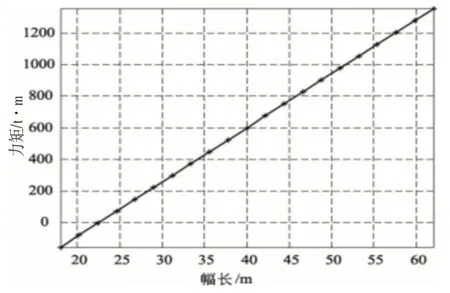
图5 吊臂平面内力矩与幅长的关系

回转角度和幅长发生变化时，相邻2 支腿合力也有所改变，假定吊重G一定，则生成如图6 所示的仿真曲线。不同机型的运行特性各异，由最小幅度Rmin～额定载荷下的幅度Rmax变化时，各自的最小幅度、最大幅度存在差异。

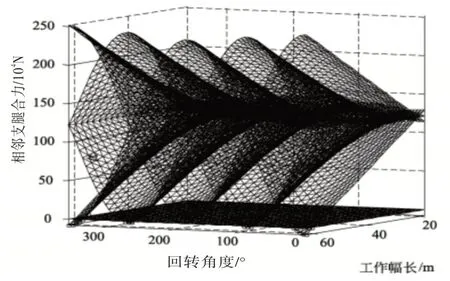
图6 相邻支腿合力与回转角和幅长的关系

假定吊装任务和工作幅长一致，重心位置随回转角变化情况，如图7所示。塔式起重机臂架头部的方向为安全方向，若方向发生改变，说明出现了安全隐患，视为危险状态。根据图7可知，带点标记的为危险区域，揭示塔式起重机在此区域运行时相邻支腿合力为零，塔式起重机可能发生倾翻事故。因此，在塔式起重机即将到达该位置时便要及时做出安全报警提示，以便优化塔式起重机的运行状态，主动规避安全隐患，必要时强行制动，禁止塔式起重机到达危险位置[2]。

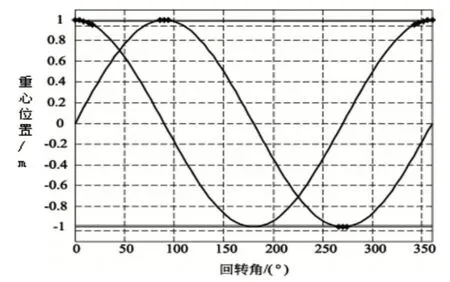
图7 塔式起重机重心位置与回转角的关系

5 结束语

综上所述，防倾翻是保障塔式起重机安全运行的重要前提，常规的力矩限制器控制方式具有被动性，本文根据主动控制、全面控制的原则，提出机械主动平衡分析方法，建立塔式起重机械相邻2支腿合力的计算模型，并结合塔式起重机的运行状态确定临界倾翻判定条件。根据临界倾翻判定条件，塔式起重机可及时做出安全报警提示，并优化自身运行状态，实现主动规避安全隐患，必要时强行制动；该研究极具有实用性。