Schwarz-Christoffel变换及其应用分析

李浩希

（华南理工大学，广东 广州 510641）

0 引言

Schwarz-Christoffel 变换在计算复杂多边形边界的数值方法中具有重要意义。学者对其进行了深入的研究，对于推动Schwarz-Christoffel 变换的应用具有重要启示。

Howe[1]提出了一种高效的数值方法，用于计算复杂多边形边界的Schwarz-Christoffel 变换方程的常数，它采用了直接搜索单纯性技术来最小化多边形尺寸误差的平方和，同时使用高斯-雅各比求积公式来评估误差函数的元素。Hu[2]开发出能实现Schwarz-Christoffel共形变换的双连通多边形区域的软件。该软件选择计算参数准确性高、计算速度快、映射“拥挤”区域的能力强，解决了与映射函数相关的所谓附加参数问题，并评估正向和反向映射。Natarajan[3]利用Schwarz-Christoffel 映射将多边形域映射到单位圆盘，并采用基于单位圆盘的中点求积规则。这一方法避免了通常需要的两级等参映射，并确保雅可比矩阵的正定性。并在多边形有限元的背景下，对一些基准问题进行了数值计算，结果表明所提出的方法能够获得准确的结果。崔建斌等[4]研究了Schwarz-Christoffel变换及其数值解法，采用Levenberg-Marquardt 算法求解非线性系统中的变换参数，针对奇异积分问题进行了区间细分和高斯-雅各比型积分的校正，提高了计算的精度，并用算例验证了该方法的可行性。

综上所述，学者们提出了高效的理论和数值方法来计算复杂多边形边界的变换常数，并开发了软件来实现Schwarz-Christoffel 共形映射。这些研究为Schwarz-Christoffel 变换的应用和改进提供了有价值的参考。本文对Schwarz-Christoffel 变换的概念、原理进行介绍，并分析其应用价值。

1 Schwarz-Christoffel变换简介

1.1 基本概念

Schwarz-Christoffel(SC)变换是使用解析函数将一个平面上复杂形状的几何体映射到另一个平面上得到简单形状的几何体的映射方法。它由数学家Hermann Schwarz 和Elwin Christoffel 在19 世纪末提出。其基本思想是通过利用已知几何图形边界与所求解析函数在边界上的值之间的关系，得到该函数在该几何区域内的值，并通过求解特定的常微分方程，将这个解析函数映射到多边形区域内，从而可以方便地求解该多边形区域内的问题。

在复平面Z上的多边形有N条边，它的顶点和内角分别为Zi和παi()i= 1,2,…,N。将T 平面上几何体上的点映射到Z平面上的Schwarz-Christoffel变换公式为[5]：

式中：K——形状系数；

C——位置系数；

παi——Z平面上多边形的内角；

ai——T平面x轴上的点。

1.2 变换示意

对椭圆和正方形映射到单位圆的Schwarz-Christoffel 变换进行介绍。通过将椭圆形和正方形变换成简单的圆形，可以更方便地进行相关的计算和分析。

（1）椭圆至单位圆的Schwarz-Christoffel变换

Tobin[6]提出由椭圆形至单位圆的Schwarz-Christoffel变换，设椭圆形的半长轴长为a，半短轴长为b，(z=x+yi)为平面上椭圆形范围内点的坐标（坐标应该有两个值？，这是不是“坐标方程”）。由椭圆形至单位圆的Schwarz-Christoffel变换如下：

式中：

椭圆形通过上述Schwarz-Christoffel 变换共形映射到圆形的过程如图1所示。

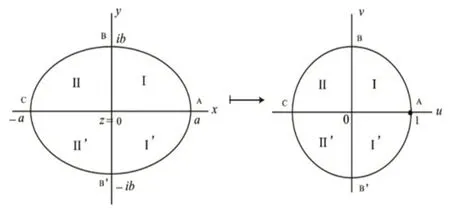
图1 椭圆至单位圆的SC变换示意图[11]

（2）正方形至单位圆的Schwarz-Christoffel变换

Chamberlain Fong[7]提出由正方形至圆形的Schwarz-Christoffel 变换，坐标在范围x∈[- 1,1 ],y∈[- 1,1 ]内的单位正方形至单位圆的Schwarz-Christoffel映射如下所示：

其中:

通过公式即可将椭圆形或正方形共形映射到单位圆。

2 Schwarz-Christoffel工具箱及其作用

2.1 Schwarz-Christoffel工具箱

SC Toolbox 即为Schwarz-Christoffel 工具箱，Schwarz-Christoffel 工具箱提供了调用函数和图形界面两种方式来输入图形信息，并将输入的图形进行Schwarz-Christoffel共形映射。

Schwarz-Christoffel 工具箱的前身是SCPACK，SCPACK 是L.N.Trefethen 在20 世纪80 年代早期开发的基于Fortran 编程语言的程序。Schwarz-Christoffel 工具箱在SCPACK 的基础上加入了交互功能以及可视化功能，而且也不需要用户进行编程。使得程序在计算Schwarz-Christoffel共形映射时更加直观便捷。

Schwarz-Christoffel 共形映射是将一个平面的上半平面映射成另一个平面上的多角形区域，当多角形的顶点大于3 时，映射函数的求取就已经变得十分困难了，依靠传统解析方法往往很难解出映射函数。基于MATLAB 编程的Schwarz-Christoffel 工具箱为这一类问题的求解提供了可能，可以用来求解复杂多边形（包括无边界区域、逻辑四边形和通道）对应的Schwarz-Christoffel映射函数。Schwarz-Christoffel工具箱包括一个用于在具有分段常数边界条件的此类区域上可以快速求解拉普拉斯方程的模块，这是它快速求解出图形对应的Schwarz-Christoffel 映射函数的基础。除此之外，Schwarz-Christoffel 工具箱还可以通过交互式界面进行图形信息输入、对图形进行Schwarz-Christoffel 共形映射等操作。

2.2 Schwarz-Christoffel工具箱的作用

应用Schwarz-Christoffel 工具箱，可以将多边形的顶点坐标作为所要转换的目标图形坐标通过polygon指令输入Schwarz-Christoffel 工具箱中；再通过diskmap指令构造一个由多边形向单位圆的共形映射；之后再通过center指令定义转换后的单位圆圆心坐标。

除了将图形信息通过调用polygon 指令输入之外，还可以通过scgui 指令在交互式界面中画出目标形状，然后再通过可视化操作界面转换为单位圆。

通过Schwarz-Christoffel Toolbox 转换前后的多边形如图2所示。

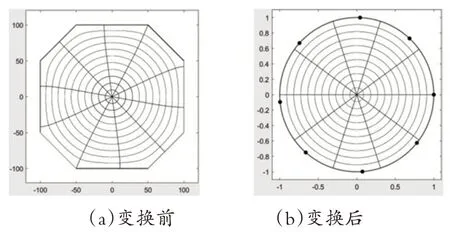
图2 通过Schwarz-Christoffel Toolbox变换前后的多边形

在对图形成功变换后，可以通过evalinv 指令得到原图形变换后位于单位圆内的等效坐标，也可以通过eval指令由单位圆上的点得到变换前该点的原坐标。

通过上述操作即可求得任意多边形到单位圆的Schwarz-Christoffel共形映射。

综上所述，Schwarz-Christoffel 工具箱可以通过输入多边形的顶点坐标来实现多边形到单位圆的Schwarz-Christoffel 共形映射。它提供了方便的指令和交互式界面，使得转换过程更加直观和可视化。通过Schwarz-Christoffel Toolbox，我们可以快速而准确地获得所需的共形映射结果。这为多边形几何形状的分析和处理提供了有力的工具和方法。

3 Schwarz-Christoffel变换的应用

Schwarz-Christoffel 变换通常用于解决有界几何区域的变形问题，以及求解该区域中的电势、热势等物理问题。其在数学、物理学、工程学、计算机科学等领域都有广泛应用。

3.1 在电气领域的应用

Balakrishnan[8]基于Schwarz-Christoffel 变换提出计算磁路中气隙磁阻的方法。该方法应用于示例配置的电感计算，并通过与基于有限元数值分析方法的计算结果进行比较，验证了其有效性。Fosset[9]讨论了在电化学问题中使用坐标变换的实用性，特别是与微电极上的非线性扩散相关的问题。使用Schwarz-Christoffel变换得到了双带电极稳态极限电流的精确表达式，并通过实验证明了数字模拟的准确性。

3.2 在流体力学领域的应用

Hasheminejad[10]基于Schwarz-Christoffel 变换，对填充水平圆柱形容器的自由液体横向振荡特性进行研究；通过精确的二维流体动力学分析，考虑了不可压缩液体和不同挡板配置；并研究了填充水平、挡板布置和长度对振荡频率和流体压力的影响；还讨论了方法的收敛性和结果的有效性。Chahar[11]基于Schwarz-Christoffel变换，采用逆方法得出了一种精确解，用于描述通过均匀各向同性多孔介质下的浅层排水层的弧形渠道渗流问题。此外，解还包括描述渠道轮廓形状和施压线轨迹的一组参数方程。

3.3 在材料领域的应用

Wang[12]基于Schwarz-Christoffel 变换，在半无限各向同性介质中，将远场III 模式加载下斜向边缘裂纹附近的螺型位错映射到应用加载下的自由表面附近的螺型位错简单情况，并推导了复杂势、应力场、应力强度因子、位错图像力、应变能等。

综上所述，Schwarz-Christoffel 变换通常应用于解决有界几何区域的变形问题，以及求解该区域中的电势、热势、流势等物理问题，是一种广泛应用的数学工具，在各个领域中都有其独特的应用。

4 结束语

本文为了分析Schwarz-Christoffel 变换的应用价值，在介绍其基本原理的基础上，分析Schwarz-Christoffel 工具箱及其在实现Schwarz-Christoffel 变换方面具有的重要作用，并介绍Schwarz-Christoffel 变换在电气领域、流体力学领域和材料领域的应用。分析认为，Schwarz-Christoffel 变换可解决有界几何区域的变形问题，以及求解该区域中的电势、热势、流势等物理问题，是一种广泛应用的数学工具，在各个领域中都有其独特的应用。随着Schwarz-Christoffel 变换继续发展和应用，它将在更广泛的工程和科学领域中发挥重要作用，并为实际问题的解决提供创新和有效的解决方案。